Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Colesanti, Andrea
Livshyts, Galyna V.
and
Marsiglietti, Arnaud
2017.
On the stability of Brunn–Minkowski type inequalities.
Journal of Functional Analysis,
Vol. 273,
Issue. 3,
p.
1120.
Milman, Vitali
and
Rotem, Liran
2017.
Convexity and Concentration.
Vol. 161,
Issue. ,
p.
361.
Artstein-Avidan, Shiri
and
Katzin, David
2018.
Isotropic measures and maximizing ellipsoids: Between John and Loewner.
Proceedings of the American Mathematical Society,
Vol. 146,
Issue. 12,
p.
5379.
Eskenazis, Alexandros
Nayar, Piotr
and
Tkocz, Tomasz
2018.
Gaussian mixtures: Entropy and geometric inequalities.
The Annals of Probability,
Vol. 46,
Issue. 5,
Nayar, Piotr
and
Tkocz, Tomasz
2019.
On a convexity property of sections of the cross-polytope.
Proceedings of the American Mathematical Society,
Vol. 148,
Issue. 3,
p.
1271.
Cordero-Erausquin, Dario
and
Rotem, Liran
2020.
Geometric Aspects of Functional Analysis.
Vol. 2256,
Issue. ,
p.
247.
Milman, Vitali
and
Rotem, Liran
2020.
Novel View on Classical Convexity Theory.
Zurnal matematiceskoj fiziki, analiza, geometrii,
Vol. 16,
Issue. 3,
p.
291.
Chen, Shibing
Huang, Yong
Li, Qi-Rui
and
Liu, Jiakun
2020.
The L-Brunn-Minkowski inequality for p < 1.
Advances in Mathematics,
Vol. 368,
Issue. ,
p.
107166.
Putterman, Eli
2021.
Equivalence of the local and global versions of the L-Brunn-Minkowski inequality.
Journal of Functional Analysis,
Vol. 280,
Issue. 9,
p.
108956.
Eskenazis, Alexandros
and
Moschidis, Georgios
2021.
The dimensional Brunn–Minkowski inequality in Gauss space.
Journal of Functional Analysis,
Vol. 280,
Issue. 6,
p.
108914.
Kolesnikov, Alexander
and
Milman, Emanuel
2022.
Local 𝐿^{𝑝}-Brunn–Minkowski inequalities for 𝑝<1.
Memoirs of the American Mathematical Society,
Vol. 277,
Issue. 1360,
Artstein-Avidan, Shiri
and
Putterman, Eli
2022.
Some New Positions of Maximal Volume of Convex Bodies.
La Matematica,
Vol. 1,
Issue. 4,
p.
765.
Kolesnikov, Alexander V
and
Livshyts, Galyna V
2022.
On the Local Version of the Log-Brunn–Minkowski Conjecture and Some New Related Geometric Inequalities.
International Mathematics Research Notices,
Vol. 2022,
Issue. 18,
p.
14427.
Hernández Cifre, María A.
and
Lucas, Eduardo
2022.
On Discrete LOG-Brunn--Minkowski Type Inequalities.
SIAM Journal on Discrete Mathematics,
Vol. 36,
Issue. 3,
p.
1748.
Wang, He Jun
2022.
Continuity of the Solution to the Lp Minkowski Problem in Gaussian Probability Space.
Acta Mathematica Sinica, English Series,
Vol. 38,
Issue. 12,
p.
2253.
Livshyts, Galyna
2023.
A universal bound in the dimensional Brunn-Minkowski inequality for log-concave measures.
Transactions of the American Mathematical Society,
Cordero-Erausquin, Dario
and
Rotem, Liran
2023.
Improved log-concavity for rotationally invariant measures of symmetric convex sets.
The Annals of Probability,
Vol. 51,
Issue. 3,
Yang, Yunlong
Jiang, Nan
and
Zhang, Deyan
2023.
Notes on the log-Brunn-Minkowski inequality.
Acta Mathematica Scientia,
Vol. 43,
Issue. 6,
p.
2333.
Wang, Hejun
2024.
On Existence of the Even Lp Gaussian Minkowski Problem for p > n.
Chinese Annals of Mathematics, Series B,
Vol. 45,
Issue. 2,
p.
179.
Roysdon, Michael
and
Xing, Sudan
2024.
On Multiple $$L_p$$-Curvilinear-Brunn–Minkowski Inequalities.
The Journal of Geometric Analysis,
Vol. 34,
Issue. 7,
 $n$ would imply the log-BMI and, therefore, the B-conjecture for any even log-concave measure in dimension
$n$ would imply the log-BMI and, therefore, the B-conjecture for any even log-concave measure in dimension  $n$. As a consequence, we prove the log-BMI and the B-conjecture for any even log-concave measure in the plane. Moreover, we prove that the log-BMI reduces to the following: for each dimension
$n$. As a consequence, we prove the log-BMI and the B-conjecture for any even log-concave measure in the plane. Moreover, we prove that the log-BMI reduces to the following: for each dimension  $n$, there is a density
$n$, there is a density 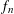 $f_{n}$, which satisfies an integrability assumption, so that the log-BMI holds for parallelepipeds with parallel facets, for the density
$f_{n}$, which satisfies an integrability assumption, so that the log-BMI holds for parallelepipeds with parallel facets, for the density 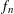 $f_{n}$. As a byproduct of our methods, we study possible log-concavity of the function
$f_{n}$. As a byproduct of our methods, we study possible log-concavity of the function 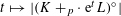 $t\mapsto |(K+_{p}\cdot ~\text{e}^{t}L)^{\circ }|$, where
$t\mapsto |(K+_{p}\cdot ~\text{e}^{t}L)^{\circ }|$, where 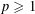 $p\geqslant 1$ and
$p\geqslant 1$ and 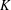 $K$,
$K$, 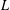 $L$ are symmetric convex bodies, which we are able to prove in some instances and, as a further application, we confirm the variance conjecture in a special class of convex bodies. Finally, we establish a non-trivial dual form of the log-BMI.
$L$ are symmetric convex bodies, which we are able to prove in some instances and, as a further application, we confirm the variance conjecture in a special class of convex bodies. Finally, we establish a non-trivial dual form of the log-BMI.

