No CrossRef data available.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 02 August 2018
Given any positive integers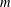 
$m$
and 
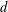$d$
, we say a sequence of points 
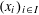$(x_{i})_{i\in I}$
in 
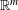$\mathbb{R}^{m}$
is Lipschitz-
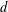$d$
-controlling if one can select suitable values 
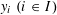$y_{i}\;(i\in I)$
such that for every Lipschitz function 
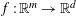$f\,:\,\mathbb{R}^{m}\,\rightarrow \,\mathbb{R}^{d}$
there exists 
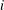$i$
with 
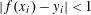$|f(x_{i})\,-\,y_{i}|\,<\,1$
. We conjecture that for every 
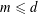$m\leqslant d$
, a sequence 
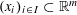$(x_{i})_{i\in I}\subset \mathbb{R}^{m}$
is 
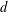$d$
-controlling if and only if We prove that this condition is necessary and a slightly stronger one is already sufficient for the sequence to be 
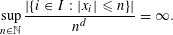$$\begin{eqnarray}\displaystyle \sup _{n\in \mathbb{N}}\frac{|\{i\in I:|x_{i}|\leqslant n\}|}{n^{d}}=\infty . & & \displaystyle \nonumber\end{eqnarray}$$
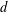$d$
-controlling. We also prove the conjecture for 
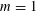$m=1$
.
Full text views reflects PDF downloads, PDFs sent to Google Drive, Dropbox and Kindle and HTML full text views.
* Views captured on Cambridge Core between 02nd August 2018 - 20th April 2021. This data will be updated every 24 hours.