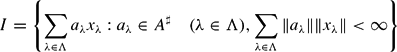Research Article
The fine Tate–Shafarevich group
-
- Published online by Cambridge University Press:
- 12 February 2007, pp. 1-12
-
- Article
- Export citation
Efficient evaluation of the Brauer–Manin obstruction
-
- Published online by Cambridge University Press:
- 12 February 2007, pp. 13-23
-
- Article
- Export citation
HNN extensions of inverse semigroups with zero
-
- Published online by Cambridge University Press:
- 12 February 2007, pp. 25-39
-
- Article
- Export citation
On generation of the root lattice by roots
-
- Published online by Cambridge University Press:
- 12 February 2007, pp. 41-45
-
- Article
- Export citation
Quasicomponents in topos theory: the hyperpure, complete spread factorization
-
- Published online by Cambridge University Press:
- 12 February 2007, pp. 47-62
-
- Article
- Export citation
The smallest subgroup whose invariants are hit by the Steenrod algebra
-
- Published online by Cambridge University Press:
- 12 February 2007, pp. 63-71
-
- Article
- Export citation
On Several types of universal invariants of framed links and 3-manifolds derived from Hopf algebras
-
- Published online by Cambridge University Press:
- 12 February 2007, pp. 73-92
-
- Article
- Export citation
Numerical index of Banach spaces and duality
-
- Published online by Cambridge University Press:
- 12 February 2007, pp. 93-102
-
- Article
- Export citation
A pair of non-homeomorphic product measures on the Cantor set
-
- Published online by Cambridge University Press:
- 12 February 2007, pp. 103-110
-
- Article
- Export citation
Pseudo-amenable and pseudo-contractible Banach algebras
-
- Published online by Cambridge University Press:
- 12 February 2007, pp. 111-123
-
- Article
- Export citation
Complete minimal hypersurfaces in
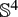 with zero Gauss–Kronecker curvature
with zero Gauss–Kronecker curvature
-
- Published online by Cambridge University Press:
- 12 February 2007, pp. 125-132
-
- Article
- Export citation
Zeros of differences of meromorphic functions
-
- Published online by Cambridge University Press:
- 12 February 2007, pp. 133-147
-
- Article
- Export citation
The support of pseudomeasures on
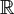
-
- Published online by Cambridge University Press:
- 12 February 2007, pp. 149-152
-
- Article
- Export citation
A combinatorial formula for homogeneous moments
-
- Published online by Cambridge University Press:
- 12 February 2007, pp. 153-160
-
- Article
- Export citation
Wigner–von Neumann perturbations of a periodic potential: spectral singularities in bands
-
- Published online by Cambridge University Press:
- 12 February 2007, pp. 161-183
-
- Article
- Export citation
Automatically closed prime ideals
-
- Published online by Cambridge University Press:
- 12 February 2007, pp. 185-192
-
- Article
- Export citation


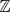 -basis of the lattice that it generates.
-basis of the lattice that it generates.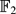 -vector space and let
-vector space and let 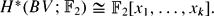 . The result is some aspect of an algebraic version of the classical conjecture that
. The result is some aspect of an algebraic version of the classical conjecture that 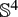 with zero Gauss–Kronecker curvature
with zero Gauss–Kronecker curvature
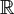
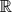 with support in the closed set
with support in the closed set 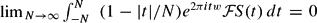 uniformly for
uniformly for