Research Article
One-transversal families
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 447-451
-
- Article
- Export citation
Partitions of a finite set into structured subsets
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 453-458
-
- Article
- Export citation
Semi-automorphisms of Hadamard matrices
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 459-473
-
- Article
- Export citation
Some remarks on a paper by Vizing on critical graphs
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 475-483
-
- Article
- Export citation
Combinatorial applications of an inequality from statistical mechanics
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 485-495
-
- Article
- Export citation
The simplicial extension theorem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 497-498
-
- Article
- Export citation
Linear forms in algebraic points of Abelian functions. I
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 499-513
-
- Article
- Export citation
Some extremal properties of convex sets
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 515-524
-
- Article
- Export citation
A proof of a theorem of Valentine
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 525-528
-
- Article
- Export citation
Almost ellipsoidal sections and projections of convex bodies
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 529-546
-
- Article
- Export citation
A further result on the existence of periodic solutions of the equation
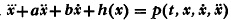
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 547-551
-
- Article
- Export citation
Some results on the decomposability of the distribution of quadratic expressions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 553-558
-
- Article
- Export citation
On the superposition of gravitational waves
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 559-565
-
- Article
- Export citation
The critical coupling of modes in a tapered earth-ionosphere wave guide
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 567-580
-
- Article
- Export citation
A two turning-point problem in fluid mechanics
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 581-590
-
- Article
- Export citation
Arrivals associated with a class of self-similar problems in elastodynamics
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 591-607
-
- Article
- Export citation
A note on variational theorems in non-linear elastostatics
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 609-615
-
- Article
- Export citation
Front matter
PSP volume 77 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 77 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b4
-
- Article
-
- You have access
- Export citation


 and
and 
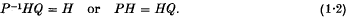
 of meromorphic functions on C
of meromorphic functions on C