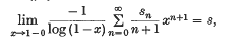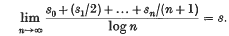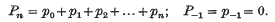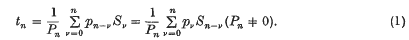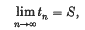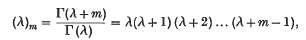Research Article
Locally nilpotent ideals of a Lie algebra‡
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 257-272
-
- Article
- Export citation
Still another way to calculate representations of the three-dimensional pure rotation group
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 273-275
-
- Article
- Export citation
Inhomogeneous minimum of indefinite quaternary quadratic forms†
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 277-290
-
- Article
- Export citation
Asymmetric inequalities for non-homogeneous ternary quadratic forms†
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 291-303
-
- Article
- Export citation
On a conjecture of B. L. van der Waerden
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 305-309
-
- Article
- Export citation
On the convex kernel of a compact set
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 311-313
-
- Article
- Export citation
The direct image of a vector bundle
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 315-334
-
- Article
- Export citation
Topological degree of non-compact mappings
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 335-347
-
- Article
- Export citation
Symmetric products of the circle
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 349-352
-
- Article
- Export citation
Collapsing three-dimensional convex polyhedra
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 353-357
-
- Article
- Export citation
On operators which depend on some parameter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 359-366
-
- Article
- Export citation
Corrigendum
Singular measures with absolutely continuous convolution squares.†(Corrigendum)
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 367-368
-
- Article
-
- You have access
- Export citation
Research Article
On quadrics through five real points
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 369-388
-
- Article
- Export citation
On the pseudoprimes of the form ax + b
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 389-392
-
- Article
- Export citation
Summability by Dirichlet convolutions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 393-400
-
- Article
- Export citation
A Tauberian theorem for the logarithmic method of summation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 401-405
-
- Article
- Export citation
On the non-absolute summability of a Fourier series and the conjugate of a Fourier series by a Nörlund method
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 407-411
-
- Article
- Export citation
Complex potentials in shallow shells of revolution
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 413-424
-
- Article
- Export citation
Generalized Neumann expansions involving hypergeometric functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 425-429
-
- Article
- Export citation
Generating functions of Jacobi polynomials
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 431-433
-
- Article
- Export citation

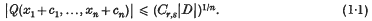
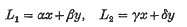


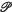 if, whenever
if, whenever 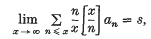
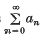 is said to be summable (
is said to be summable (