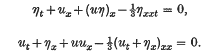Research Article
Well-quasi-orderings and sets of finite sequences
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-10
-
- Article
- Export citation
Anticritical graphs
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 11-18
-
- Article
- Export citation
On complete subgraphs of different orders
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 19-24
-
- Article
- Export citation
A new combinatorial approach to M24
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 25-42
-
- Article
- Export citation
General asymptotic distributions for additive arithmetic functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 43-54
-
- Article
- Export citation
Linear forms in algebraic points of Abelian functions. II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 55-70
-
- Article
- Export citation
Spectral asymmetry and Riemannian geometry. III
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 71-99
-
- Article
- Export citation
Structure of a foliated neighbourhood
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 101-110
-
- Article
- Export citation
Strictly singular and cosingular operators
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 111-115
-
- Article
- Export citation
Integrability of singular distributions on Banach manifolds
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 117-128
-
- Article
- Export citation
On the Lusternik–Schnirelmann category of Grassmannians
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 129-134
-
- Article
- Export citation
Derangements and Laguerre polynomials
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 135-143
-
- Article
- Export citation
The wave front set of the solution of a simple initial-boundary value problem with glancing rays
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 145-159
-
- Article
- Export citation
A class of approximate exterior rotating solutions of Einstein's equations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 161-166
-
- Article
- Export citation
A model for the two-way propagation of water waves in a channel
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 167-182
-
- Article
- Export citation
Magnetohydrodynamic flow past sources in the presence of a wall
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 183-193
-
- Article
- Export citation
Front matter
PSP volume 79 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 79 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b3
-
- Article
-
- You have access
- Export citation

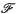 be a family of distinct subsets of
be a family of distinct subsets of 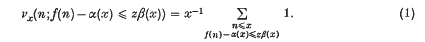
 of Abelian functions. This section deals with properties of more general functions holomorphic on C
of Abelian functions. This section deals with properties of more general functions holomorphic on C
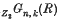 is strictly less than the maximum possible value dim
is strictly less than the maximum possible value dim  the number of possible derangements of the set i.e. permutations in which no object occupies a site originally occupied by an object of the same type. A formula is found for
the number of possible derangements of the set i.e. permutations in which no object occupies a site originally occupied by an object of the same type. A formula is found for 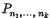 in terms of Laguerre polynomials, and some of its implications are considered.
in terms of Laguerre polynomials, and some of its implications are considered.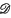 ′ (Ω) and
′ (Ω) and