Hostname: page-component-8448b6f56d-m8qmq Total loading time: 0 Render date: 2024-04-24T05:43:07.289Z Has data issue: false hasContentIssue false
  • English
  • Français

On the method for solution of unsteady thermal boundary-layers in case of two-dimensional low-speed flows

Published online by Cambridge University Press:  24 October 2008

Milan Ð. Ðurić
Milan Ð. Ðurić
Affiliation:
Institute of Mathematics, Belgrade
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper is dedicated to the question of solving unsteady thermal boundary-layers in the case of two-dimensional low-speed flows, provided that the difference between the temperature of the stream and that of the wall is not too great (so that the density is sensibly constant) and that the change in the wall temperature Tw (x, t) takes place at the same instant as the body is set into motion. The velocity boundary-layer is uncoupled from the thermal one and can be considered separately. In paper (2) is given the method for obtaining the velocity field (u, v). The temperature field T depends on the velocity field and can be obtained only after this one. The method (2) being available for this purpose assuming the difference between the temperature of the wall Tw (x, t) and that of the main-stream T∞ in the form of

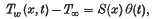
where S(x) and θ(t) are arbitrary functions of x respectively t, satisfying certain conditions required by the method.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 64 , Issue 3 , July 1968 , pp. 849 - 870
Copyright
Copyright © Cambridge Philosophical Society 1968

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Curle, N.The laminar boundary-layer equations. Oxford Math. Monographys (1962).Google Scholar
(2)Ðurić, M.A method for solution of unsteady incompressible laminar boundary layers. Public. Inst. Math. (Beograd), 6 (1966), 29–55.Google Scholar
(3)Gibellato, S.Strato limite termico attorno a una lestra piana investita da una corrente lievemente pulsante di fluido incompressible. Atti Accad. Sci. Torino, Cl. Sci. Mat. Natu. 91 (1956–1957), 152–70.Google Scholar
(4)Illingworth, C. R.Unsteady laminar flow of gas near an infinite flat plate. Proc. Cambridge Philos. Soc. 46 (1950), 603–613.CrossRefGoogle Scholar
(5)Imai, I.On the heat transfer to constant-property laminar boundary layer with powerfunction free-stream velocity and wall temperature distribution. Quart. Appl. Math. 16 (1958), 33–45.Google Scholar
(6)Lighthill, M. J.The response of laminar skin friction and heat transfer to fluctuations in the stream velocity. Proc. Roy. Soc. Ser. A 224 (1954), 1–23.Google Scholar
(7)Loitsianskii, L. G.The laminar boundary layer. Moscow (1962).Google Scholar
(8)Rosenhead, L.Laminar boundary layers. Fluid Motion Memoirs. Oxford (1963).Google Scholar
(9)Sarma, G. N.The unsteady thermal boundary-layer equation. Proc. Cambridge Philos. Soc. 61 (1965), 809–825.CrossRefGoogle Scholar
(10)Sarma, G. N.Solutions of unsteady boundary-layer equations. Proc. Cambridge Philos. Soc. 60 (1964), 137–158.CrossRefGoogle Scholar
(11)Sparrow, E. M.Combined effects of unsteady flight velocity and surface temperature on heat transfer. Jet Prop. 28 (1958), 403–5.Google Scholar
(12)Whittaker, T. E. and Watson, N. G.A course of modern analysis. Cambridge University Press (1946).Google Scholar