Hostname: page-component-8448b6f56d-c4f8m Total loading time: 0 Render date: 2024-04-19T20:11:59.276Z Has data issue: false hasContentIssue false
  • English
  • Français

SYMMETRIC POWER CONGRUENCE IDEALS AND SELMER GROUPS

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  14 November 2018

Haruzo Hida  and
Jacques Tilouine
Haruzo Hida
Affiliation:
Department of Mathematics, UCLA, Los Angeles, CA 90095-1555, USA (hida@math.ucla.edu)
Jacques Tilouine
Affiliation:
Département de Mathématiques, LAGA, Institut Galilée, U. Paris 13, 99 av. J.-B. Clément, Villetaneuse 93430, France (tilouine@math.univ-paris13.fr)
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove, under some assumptions, a Greenberg type equality relating the characteristic power series of the Selmer groups over 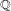$\mathbb{Q}$ of higher symmetric powers of the Galois representation associated to a Hida family and congruence ideals associated to (different) higher symmetric powers of that Hida family. We use 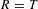$R=T$ theorems and a sort of induction based on branching laws for adjoint representations. This method also applies to other Langlands transfers, like the transfer from 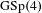$\text{GSp}(4)$ to 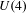$U(4)$. In that case we obtain a corollary for abelian surfaces.

Keywords

Congruence moduleHecke algebrauniversal Galois deformation ring

MSC classification

Primary: 11F33: Congruences for modular and $p$-adic modular forms 11F80: Galois representations
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 5 , September 2020 , pp. 1521 - 1572
Check for updates
Copyright
© Cambridge University Press 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author is partially supported by the NSF grant: DMS 1464106. The second author is partially supported by the ANR grant: PerCoLaTor ANR-14-CE25.

References

Arthur, J. and Clozel, L., Simple algebras, in Base Change and the Advanced Theory of the Trace Formula, Annals of Mathematics Studies (Princeton University Press, Princeton, 1989).Google Scholar
Bourbaki, N., Algèbre, Chapitre 2, (Hermann, Paris, 1962).Google Scholar
Bourbaki, N., Algèbre Commutative (Hermann, Paris, 1961–1998).Google Scholar
Clozel, L., Harris, M. and Taylor, R., Automorphy for Some ℓ-adic Lifts of Automorphic Modulo ℓ Galois Representations, Publ. Math. Inst. Hautes Études Sci. (108) (2008), 1–181. With Appendix A, summarizing unpublished work of Russ Mann, and Appendix B by Marie-France Vignéras. MR2470687.Google Scholar
Clozel, L., Représentations galoisiennes associées aux représentations automorphes autoduales de GL(n), Publ. Math. Inst. Hautes Études Sci. 73 (1991), 97–145.Google Scholar
Clozel, L. and Thorne, J., Level-raising and symmetric power functoriality, I, Compos. Math. 150(5) (2014), 729–748.Google Scholar
Clozel, L. and Thorne, J., Level-raising and symmetric power functoriality, II, Ann. of Math. (2) 181(1) (2015), 303–359.Google Scholar
Conti, A., Grande image de Galois pour les familles $p$-adiques de formes automorphes de pente positive, thèse de l’Université Paris 13, defended July 13, 2016.Google Scholar
Conti, A., Galois level and congruence ideal for $\text{GSp}_{4}$, Compos. Math., Preprint, 65 pp, to appear.Google Scholar
Darmon, H., Diamond, F. and Taylor, R., Fermat’s last theorem, in Current Developments in Mathematics, pp. 1–154 (Cambridge, MA, 1995). Int. Press, Cambridge, MA, 1994.Google Scholar
Diamond, F., The Taylor–Wiles construction and multiplicity one, Invent. Math. 128 (1997), 379–391.Google Scholar
Genestier, A. and Tilouine, J., Systèmes de Taylor–Wiles pour GSp(4), in Formes automorphes II, Le cas du groupe GSp(4), Astérisque, Volume 302, pp. 177–290 (Soc. Math. France, Paris, 2005).Google Scholar
Gan, W.-T. and Takeda, S., The local Langlands conjecture for GSp(4), Ann. of Math. (2) 173 (2011), 1841–1882.Google Scholar
Geraghty, D., Modularity lifting theorems for ordinary Galois representations, Harvard Dissertation (2010).Google Scholar
Geraghty, D., Notes on modularity lifting in the ordinary case, in $p$-adic Aspects of Modular Forms, Proc. IISER Pune conference (ed. B. Balasubramaniam, H. Hida, A. Raghuram and J. Tilouine) (World Scientific Publ., 2016).Google Scholar
Harris, M. and Taylor, R., The Geometry and Cohomology of Some Simple Shimura Varieties, Annals of Mathematics Studies, Volume 151 (Princeton University Press, Princeton, NJ, 2001). With an appendix by Vladimir G. Berkovich.Google Scholar
Harron, R. and Jorza, A., On symmetric power 𝓛-invariants of Iwahori level Hilbert modular forms, Amer. J. Math. 139 (2017), 1605–1647.Google Scholar
Hida, H., Geometric Modular Forms and Elliptic Curves, second edition (World Scientific, Singapore, 2011).Google Scholar
Hida, H., Modular Forms and Galois Cohomology, Cambridge Studies in Advanced Mathematics, Volume 69 (Cambridge University Press, Cambridge, England, 2000). (A list of errata posted at www.math.ucla.edu/∼hida).Google Scholar
Hida, H., p-adic Automorphic Forms, Springer Monographs in Mathematics, (Springer, 2004).Google Scholar
Hida, H., Hecke algebras for GL1 and GL2 , Sém. de Théorie des Nombres, Paris 1984–85, Progr. Math. 63 (1986), 131–163.Google Scholar
Hida, H., Modules of congruence of Hecke algebras and L–functions associated with cusp forms, Amer. J. Math. 110 (1988), 323–382.Google Scholar
Hida, H., Control theorems of coherent sheaves on Shimura varieties of PEL type, J. Inst. Math. Jussieu 1 (2002), 1–76.Google Scholar
Hida, H., Arithmetic of adjoint L-values, in $p$-adic Aspects of Modular Forms, Proc. IISER Pune Conference (ed. S B. Balasubramaniam, H. Hida, A. Raghuram and J. Tilouine) (World Scientific Publ., 2016).Google Scholar
Hida, H. and Tilouine, J., Big image of Galois representations and congruence ideals, in Arithmetic Geometry, Proc. Workshop on Serre’s Conjecture, Hausdorff Inst. Math., Bonn (ed. Dieulefait, L., Heath-Brown, D. R., Faltings, G., Manin, Y. I., Moroz, B. Z. and Wintenberger, J.-P.), pp. 217–254 (Cambridge University Press, 2015).Google Scholar
Kim, H. H., Functoriality for the exterior square of GL4 and the symmetric fourth of GL2, J. Amer. Math. Soc. 16(1) (2003), 139–183. With Appendix 1 by Dinakar Ramakrishnan and Appendix 2 by Kim and Peter Sarnak.Google Scholar
Kim, H. H. and Shahidi, F., Cuspidality of symmetric powers with applications, Duke Math. J. 112 (2002), 177–197.Google Scholar
Kim, H. H. and Shahidi, F., Functorial products for GL2 × GL3 and the symmetric cube for GL2, Ann. of Math. (2) 155(3) (2002), 837–893. With an appendix by Colin J. Bushnell and Guy Henniart.Google Scholar
Labesse, J.-P., Changement de base CM et séries discrètes, in Stabilization of the Trace Formula, Shimura Varieties, and Arithmetic Applications (ed. Harris, M.), (Int. Press, Somerville, MA, 2009).Google Scholar
Laumon, G., Fonctions zêta des variétés de Siegel de dimension trois, in Formes Automorphes (II), le cas du groupe GSp(4), Astérisque, Volume 302 (SMF, 2005).Google Scholar
Liu, Z., $p$-adic $L$ functions for ordinary families on symplectic groups, to appear.Google Scholar
Mok, C. P., Galois representations attached to automorphic forms on GL2 over a CM field, Compos. Math. 150 (2014), 523–567.Google Scholar
Matsumura, H., Commutative Ring Theory, Cambridge Studies in Advanced Mathematics, Volume 8 (Cambridge University Press, 1986).Google Scholar
Mazur, B. and Robert, L., Local Euler characteristic, Invent. Math. 9 (1970), 201–234. with an Appendix by J. Tate.Google Scholar
Pilloni, V., Modularité formes de Siegel et surfaces abéliennes, J. Reine Angew. Math. 666 (2012), 35–82.Google Scholar
Platonov, V. and Rapinchuk, A., Algebraic Groups and Number Theory (Academic Press, 1994).Google Scholar
Polo, P. and Tilouine, J., Bernstein–Gelfand–Gelfand complexes and cohomology of nilpotent groups over ℤp, Astérisque, Volume 282 (SMF, 2002).Google Scholar
Ribet, K., A modular construction of unramified p-extensions of ℚ(𝜇p), Invent. Math. 34 (1976), 151–162.Google Scholar
Ramakrishnan, D. and Shahidi, F., Siegel modular forms of genus two attached to elliptic curves, Math. Res. Lett. 14(2) (2007), 315–332.Google Scholar
Roberts, B. and Schmidt, R., Local Newforms on GSp(4), Springer LNM, Volume 1918 (Springer, 2007).Google Scholar
Tilouine, J. and Urban, E., Several variable p-adic families of Siegel-Hilbert cusp eigensystems and their Galois representations, Ann. Sci. Éc. Norm Supér (4) 32 (1999), 499–574.Google Scholar
Tilouine, J., Deformations of Galois Representations and Hecke Algebras (Mehta Institute, AMS, 2002).Google Scholar
Tilouine, J., Nearly ordinary rank four Galois representations and p-adic Siegel modular forms, Compos. Math. 142 (2006), 1122–1156.Google Scholar
Vignéras, M.-F., On the Global Correspondence between GL(n) and a Division Algebra (Institute for Advanced Studies, Princeton, 1984).Google Scholar
Weissauer, R., Four-dimensional Galois representations, in Formes Automorphes (II), le cas du groupe GSp(4), Astérisque, Volume 302 (SMF, 2005).Google Scholar
Yoshida, H., Weil’s representations and Siegel’s modular forms, in Lectures on Harmonic Analysis on Lie Groups and Related Topics (Strasbourg, 1979), Lectures in Math., Volume 14, pp. 319–341 (Kinokuniya Book Store, Tokyo, 1982).Google Scholar
Zhang, X., Special L-values and Selmer groups of Siegel modular forms of genus 2,arXiv:1811.02031.Google Scholar