Article contents
GENERAL HYPERPLANE SECTIONS OF THREEFOLDS IN POSITIVE CHARACTERISTIC
Published online by Cambridge University Press: 12 April 2018
Abstract
In this paper, we study the singularities of a general hyperplane section 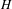 $H$ of a three-dimensional quasi-projective variety
$H$ of a three-dimensional quasi-projective variety 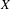 $X$ over an algebraically closed field of characteristic
$X$ over an algebraically closed field of characteristic 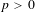 $p>0$. We prove that if
$p>0$. We prove that if 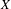 $X$ has only canonical singularities, then
$X$ has only canonical singularities, then 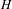 $H$ has only rational double points. We also prove, under the assumption that
$H$ has only rational double points. We also prove, under the assumption that 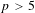 $p>5$, that if
$p>5$, that if 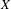 $X$ has only klt singularities, then so does
$X$ has only klt singularities, then so does 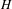 $H$.
$H$.
Keywords
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 2 , March 2020 , pp. 647 - 661
- Copyright
- © Cambridge University Press 2018
References
- 3
- Cited by


