Research Article
Uniform labelled semilattices
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 385-397
-
- Article
-
- You have access
- Export citation
A 4-chromatic graph with a special plane drawing
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-8
-
- Article
-
- You have access
- Export citation
Two notes on frames
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 257-268
-
- Article
-
- You have access
- Export citation
Effective bounds of the solutions of certain Diophantine equations
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 129-135
-
- Article
-
- You have access
- Export citation
Conjugate purity and infinite groups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 9-14
-
- Article
-
- You have access
- Export citation
A lambda calculus with naive substitution
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 269-282
-
- Article
-
- You have access
- Export citation
Decomposability of finite rings
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 136-138
-
- Article
-
- You have access
- Export citation
Residual finiteness and ‘free’ distributively generated near-rings
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 398-400
-
- Article
-
- You have access
- Export citation
The automorphism group of the semigroup of finite complexes of a periodic abelian group
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 15-22
-
- Article
-
- You have access
- Export citation
Trace polynomials of words in special linear groups
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 401-412
-
- Article
-
- You have access
- Export citation
On the existence of sulutions of the equation Lx ∞ Nx and a coincidence degree theory
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 139-173
-
- Article
-
- You have access
- Export citation
Radicals related to the Brown-McCoy radical in some varieties of algebras
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 283-294
-
- Article
-
- You have access
- Export citation
Harmonic functions for a class of Markov chains
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 413-422
-
- Article
-
- You have access
- Export citation
A maximum principle
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 23-26
-
- Article
-
- You have access
- Export citation
Free groups, symmetric and reduced products
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 174-178
-
- Article
-
- You have access
- Export citation
Orthologic Desargues' figure
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 295-302
-
- Article
-
- You have access
- Export citation
Special pairs of semi-bilogic and bilogic tetrahedra
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 303-308
-
- Article
-
- You have access
- Export citation
Nilpotents and units in skew polynomial rings over commutative rings
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 423-426
-
- Article
-
- You have access
- Export citation
Characterizations of collectively precompact and semi-precompact opterators on topological vector spaces
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 179-188
-
- Article
-
- You have access
- Export citation
On Sylow graphs
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 27-38
-
- Article
-
- You have access
- Export citation

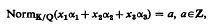
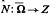 is a (possiblv nonlinear) mapping and Ω is a bounded open subset of
is a (possiblv nonlinear) mapping and Ω is a bounded open subset of 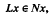
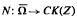 and
and