Research Article
The multidimensional fundamental theorem of calculus
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 143-170
-
- Article
-
- You have access
- Export citation
The strong radical and the left regular representation
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-9
-
- Article
-
- You have access
- Export citation
Typical Convex Sets of Convex Sets
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 287-290
-
- Article
-
- You have access
- Export citation
Pointwise Convergence of Trigonometric Series
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 291-300
-
- Article
-
- You have access
- Export citation
Permutation polynomials in several variables over residue class rings
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 171-175
-
- Article
-
- You have access
- Export citation
The kernel of integral cup product
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 10-15
-
- Article
-
- You have access
- Export citation
Growth sequences of finite semigroups
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 16-20
-
- Article
-
- You have access
- Export citation
Consequences of the Pseudo Orbits Tracing Property and Expansiveness
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 301-313
-
- Article
-
- You have access
- Export citation
A geometrical approach to approximations by continued fractions
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 176-186
-
- Article
-
- You have access
- Export citation
A Note On the Hadamard Kth Root of a Rational Function
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 314-327
-
- Article
-
- You have access
- Export citation
A class of hypergeometric polynomials
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 187-198
-
- Article
-
- You have access
- Export citation
Proper efficiency and duality for vector valued optimization problems
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 21-34
-
- Article
-
- You have access
- Export citation
Irreducibility of the analytic continuation of the principal series of a free group
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 199-210
-
- Article
-
- You have access
- Export citation
Extension of Riesz homomorphisms. III
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 35-46
-
- Article
-
- You have access
- Export citation
On Fixed Points of Asymptotically Regular Mappings
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 328-346
-
- Article
-
- You have access
- Export citation
Convolutions of Distributions With Exponential and Subexponential Tails
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 347-365
-
- Article
-
- You have access
- Export citation
Coin tossing and sum sets
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 211-219
-
- Article
-
- You have access
- Export citation
Modular inverse semigroups
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 47-63
-
- Article
-
- You have access
- Export citation
Congruences and Green's relations on eventually regular semigroups
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 64-69
-
- Article
-
- You have access
- Export citation
A Characterization and a Variational Inequality for the Multivariate Normal Distribution
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 366-374
-
- Article
-
- You have access
- Export citation

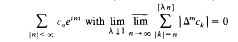 for some nonnegative integer
for some nonnegative integer 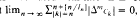 , where {
, where {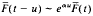 and
and 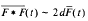 as
as 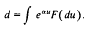 .
.