Let 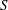 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}S$ be a semigroup. Elements
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}S$ be a semigroup. Elements 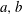 $a,b$ of
$a,b$ of 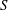 $S$ are
$S$ are 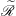 $\widetilde{\mathscr{R}}$-related if they have the same idempotent left identities. Then
$\widetilde{\mathscr{R}}$-related if they have the same idempotent left identities. Then 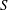 $S$ is weakly left ample if (1) idempotents of
$S$ is weakly left ample if (1) idempotents of 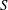 $S$ commute, (2)
$S$ commute, (2) 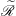 $\widetilde{\mathscr{R}}$ is a left congruence, (3) for any
$\widetilde{\mathscr{R}}$ is a left congruence, (3) for any 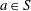 $a \in S$,
$a \in S$,  $a$ is
$a$ is 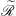 $\widetilde{\mathscr{R}}$-related to a (unique) idempotent, say
$\widetilde{\mathscr{R}}$-related to a (unique) idempotent, say 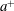 $a^+$, and (4) for any element
$a^+$, and (4) for any element  $a$ and idempotent
$a$ and idempotent  $e$ of
$e$ of  $S$,
$S$, 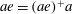 $ae=(ae)^+a$. Elements
$ae=(ae)^+a$. Elements 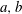 $a,b$ of
$a,b$ of 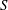 $S$ are
$S$ are 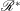 $\mathscr{R}^*$-related if, for any
$\mathscr{R}^*$-related if, for any 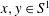 $x,y \in S^1$,
$x,y \in S^1$, 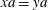 $xa=ya$ if and only if
$xa=ya$ if and only if 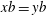 $xb=yb$. Then
$xb=yb$. Then 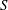 $S$ is left ample if it satisfies (1), (3) and (4) relative to
$S$ is left ample if it satisfies (1), (3) and (4) relative to 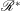 $\mathscr{R}^*$ instead of
$\mathscr{R}^*$ instead of 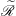 $\widetilde{\mathscr{R}}$. Further,
$\widetilde{\mathscr{R}}$. Further, 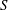 $S$ is (weakly) ample if it is both (weakly) left and right ample. We establish several characterizations of these classes of semigroups. For weakly left ample ones we provide a construction of all such semigroups with zero all of whose nonzero idempotents are primitive. Among characterizations of weakly ample semigroups figure (strong) semilattices of unipotent monoids, and among those for ample semigroups, (strong) semilattices of cancellative monoids. This describes the structure of these two classes of semigroups in an optimal way, while, for the ‘one-sided’ case, the problem of structure remains open.
$S$ is (weakly) ample if it is both (weakly) left and right ample. We establish several characterizations of these classes of semigroups. For weakly left ample ones we provide a construction of all such semigroups with zero all of whose nonzero idempotents are primitive. Among characterizations of weakly ample semigroups figure (strong) semilattices of unipotent monoids, and among those for ample semigroups, (strong) semilattices of cancellative monoids. This describes the structure of these two classes of semigroups in an optimal way, while, for the ‘one-sided’ case, the problem of structure remains open.