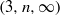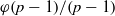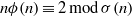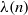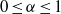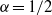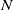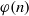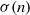Research Article
A VARIANT OF HOFSTADTER’S SEQUENCE AND FINITE AUTOMATA
- Part of:
-
- Published online by Cambridge University Press:
- 03 May 2013, pp. 1-8
-
- Article
-
- You have access
- Export citation
COMPLEX NUMBERS WITH BOUNDED PARTIAL QUOTIENTS
- Part of:
-
- Published online by Cambridge University Press:
- 16 April 2013, pp. 9-20
-
- Article
-
- You have access
- Export citation
CONTINUED FRACTIONS FOR A CLASS OF TRIANGLE GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 07 February 2013, pp. 21-42
-
- Article
-
- You have access
- Export citation
TWIN SQUAREFUL NUMBERS
- Part of:
-
- Published online by Cambridge University Press:
- 19 September 2012, pp. 43-51
-
- Article
-
- You have access
- Export citation
CLASSIFICATION AND SYMMETRIES OF A FAMILY OF CONTINUED FRACTIONS WITH BOUNDED PERIOD LENGTH
- Part of:
-
- Published online by Cambridge University Press:
- 03 May 2013, pp. 53-76
-
- Article
-
- You have access
- Export citation
A NOTE ON THE DISTRIBUTION FUNCTION OF
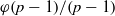 $ \varphi (\lowercase {P}-1)/(\lowercase {P}-1)$
$ \varphi (\lowercase {P}-1)/(\lowercase {P}-1)$
- Part of:
-
- Published online by Cambridge University Press:
- 16 January 2013, pp. 77-83
-
- Article
-
- You have access
- Export citation
ON A VARIATION OF A CONGRUENCE OF SUBBARAO
- Part of:
-
- Published online by Cambridge University Press:
- 04 February 2013, pp. 85-90
-
- Article
-
- You have access
- Export citation
RINGS ON WATER AND THEIR ENTROPY
- Part of:
-
- Published online by Cambridge University Press:
- 14 March 2013, pp. 91-100
-
- Article
-
- You have access
- Export citation
ON THE RANKIN–SELBERG ZETA FUNCTION
- Part of:
-
- Published online by Cambridge University Press:
- 19 September 2012, pp. 101-113
-
- Article
-
- You have access
- Export citation
RELATIONS IN THE 2-CLASS GROUP OF QUADRATIC NUMBER FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 07 February 2013, pp. 115-120
-
- Article
-
- You have access
- Export citation
APPROXIMATION OF AN ALGEBRAIC NUMBER BY PRODUCTS OF RATIONAL NUMBERS AND UNITS
- Part of:
-
- Published online by Cambridge University Press:
- 07 February 2013, pp. 121-131
-
- Article
-
- You have access
- Export citation
ON THE OPTIMAL CONTINUED FRACTION EXPANSION OF A QUADRATIC SURD
- Part of:
-
- Published online by Cambridge University Press:
- 07 February 2013, pp. 133-156
-
- Article
-
- You have access
- Export citation
BETWEEN THE PROBLEMS OF PÓLYA AND TURÁN
- Part of:
-
- Published online by Cambridge University Press:
- 27 September 2012, pp. 157-171
-
- Article
-
- You have access
- Export citation
WEAK PROPER DISTRIBUTION OF VALUES OF MULTIPLICATIVE FUNCTIONS IN RESIDUE CLASSES
- Part of:
-
- Published online by Cambridge University Press:
- 04 February 2013, pp. 173-188
-
- Article
-
- You have access
- Export citation
ON DIVISIBILITY OF BINOMIAL COEFFICIENTS
- Part of:
-
- Published online by Cambridge University Press:
- 19 September 2012, pp. 189-201
-
- Article
-
- You have access
- Export citation
Front Cover (OFC, IFC) and matter
JAZ VOLUME 93 ISSUE 1-2 COVER AND FRONT MATTER
-
- Published online by Cambridge University Press:
- 03 May 2013, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
JAZ VOLUME 93 ISSUE 1-2 COVER AND BACK MATTER
-
- Published online by Cambridge University Press:
- 03 May 2013, pp. b1-b8
-
- Article
-
- You have access
- Export citation