No CrossRef data available.
Article contents
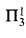 sets and
sets and 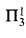 singletons
singletons
Published online by Cambridge University Press: 12 March 2014
Abstract
We extend work of H. Friedman, L. Harrington and P. Welch to the third level of the projective hierarchy. Our main theorems say that (under appropriate background assumptions) the possibility to select definable elements of non-empty sets of reals at the third level of the projective hierarchy is equivalent to the disjunction of determinacy of games at the second level of the projective hierarchy and the existence of a core model (corresponding to this fragment of determinacy) which must then contain all real numbers. The proofs use Sacks forcing with perfect trees and core model techniques.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1999


