No CrossRef data available.
Article contents
RANK AND RANDOMNESS
Published online by Cambridge University Press: 19 September 2019
Abstract
We show that for each computable ordinal 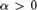 $\alpha > 0$ it is possible to find in each Martin-Löf random
$\alpha > 0$ it is possible to find in each Martin-Löf random 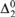 ${\rm{\Delta }}_2^0 $ degree a sequence R of Cantor-Bendixson rank α, while ensuring that the sequences that inductively witness R’s rank are all Martin-Löf random with respect to a single countably supported and computable measure. This is a strengthening for random degrees of a recent result of Downey, Wu, and Yang, and can be understood as a randomized version of it.
${\rm{\Delta }}_2^0 $ degree a sequence R of Cantor-Bendixson rank α, while ensuring that the sequences that inductively witness R’s rank are all Martin-Löf random with respect to a single countably supported and computable measure. This is a strengthening for random degrees of a recent result of Downey, Wu, and Yang, and can be understood as a randomized version of it.
Keywords
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2019


