Article contents
NORMAL NUMBERS AND COMPLETENESS RESULTS FOR DIFFERENCE SETS
Published online by Cambridge University Press: 21 March 2017
Abstract
We consider some natural sets of real numbers arising in ergodic theory and show that they are, respectively, complete in the classes 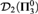 ${\cal D}_2 \left( {{\bf{\Pi }}_3^0 } \right)$ and
${\cal D}_2 \left( {{\bf{\Pi }}_3^0 } \right)$ and 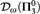 ${\cal D}_\omega \left( {{\bf{\Pi }}_3^0 } \right)$, that is, the class of sets which are 2-differences (respectively, ω-differences) of
${\cal D}_\omega \left( {{\bf{\Pi }}_3^0 } \right)$, that is, the class of sets which are 2-differences (respectively, ω-differences) of 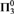 ${\bf{\Pi }}_3^0 $ sets.
${\bf{\Pi }}_3^0 $ sets.
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2017
References
REFERENCES
- 3
- Cited by


