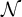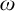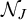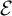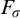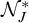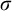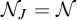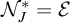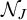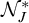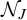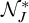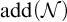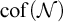1 Introduction
Many notions of topology and combinatorics of the reals have been reformulated and investigated in terms of ideals on the natural numbers (always assuming that an ideal contains all the finite sets of natural numbers). For instance, the usual notion of convergence on a topological space, which states that a sequence
![]() $\langle x_n:\, n<\omega \rangle $
in a topological space converges to a point
$\langle x_n:\, n<\omega \rangle $
in a topological space converges to a point
![]() $x\in X$
when the set
$x\in X$
when the set
![]() ${\left \{ {n<\omega } :\, {x_n\notin U} \right \}}$
is finite for any open neighborhood U of x, is generalized in terms of ideals J on the natural numbers by changing the latter requirement by
${\left \{ {n<\omega } :\, {x_n\notin U} \right \}}$
is finite for any open neighborhood U of x, is generalized in terms of ideals J on the natural numbers by changing the latter requirement by
![]() ${\left \{ {n<\omega } :\, { x_n\notin U} \right \}}\in J$
(see, e.g., [Reference Kostyrko, Šalát and Wilczyński28]). More recent and remarkable examples are the so-called selection principles, which are reformulated in terms of ideals, and show deep connections with cardinal characteristics of the real line [Reference Bukovský, Das and Šupina17, Reference Repický37, Reference Repický38, Reference Šottová and Šupina41, Reference Šupina42].
${\left \{ {n<\omega } :\, { x_n\notin U} \right \}}\in J$
(see, e.g., [Reference Kostyrko, Šalát and Wilczyński28]). More recent and remarkable examples are the so-called selection principles, which are reformulated in terms of ideals, and show deep connections with cardinal characteristics of the real line [Reference Bukovský, Das and Šupina17, Reference Repický37, Reference Repický38, Reference Šottová and Šupina41, Reference Šupina42].
In combinatorics of the real line, some classical cardinal characteristics have been reformulated in terms of ideals (and in many cases they are connected to selection principles in topology). The most natural examples are the reformulations of the bounding number
![]() ${\mathfrak {b}}_J$
and the dominating number
${\mathfrak {b}}_J$
and the dominating number
![]() ${\mathfrak {d}}_J$
in terms of an ideal J on
${\mathfrak {d}}_J$
in terms of an ideal J on
![]() $\omega $
, more concretely, with respect to the relation
$\omega $
, more concretely, with respect to the relation
![]() $\leq ^J$
on
$\leq ^J$
on
![]() ${{}^\omega \omega }$
, which states that
${{}^\omega \omega }$
, which states that
![]() $x \leq ^J y$
iff
$x \leq ^J y$
iff
![]() ${\left \{ {n<\omega } :\, {x(n)\nleq y(n)} \right \}}\in J$
. These have been investigated by, e.g., Canjar [Reference Canjar18], Blass and Mildenberger [Reference Blass and Mildenberger10], also in connection with arithmetic in the sense that, for any maximal ideal J,
${\left \{ {n<\omega } :\, {x(n)\nleq y(n)} \right \}}\in J$
. These have been investigated by, e.g., Canjar [Reference Canjar18], Blass and Mildenberger [Reference Blass and Mildenberger10], also in connection with arithmetic in the sense that, for any maximal ideal J,
![]() ${\mathfrak {b}}_J={\mathfrak {d}}_J$
is the cofinality of the ultrapower (on the dual filter of J) of
${\mathfrak {b}}_J={\mathfrak {d}}_J$
is the cofinality of the ultrapower (on the dual filter of J) of
![]() $\omega $
. Other classical cardinal characteristics have been reformulated in terms of ideals on
$\omega $
. Other classical cardinal characteristics have been reformulated in terms of ideals on
![]() $\omega $
, like the almost disjointness number [Reference Farkas and Soukup21, Reference Haga, Schrittesser and Törnquist23, Reference Raghavan and Steprāns36] and the pseudo-intersection number [Reference Borodulin-Nadzieja and Farkas13, Reference Šupina43], among others (see [Reference Hrušák25, Section 8.4]).
$\omega $
, like the almost disjointness number [Reference Farkas and Soukup21, Reference Haga, Schrittesser and Törnquist23, Reference Raghavan and Steprāns36] and the pseudo-intersection number [Reference Borodulin-Nadzieja and Farkas13, Reference Šupina43], among others (see [Reference Hrušák25, Section 8.4]).
In the present paper we offer a reformulation, in terms of ideals on
![]() $\omega $
, of the ideal of Lebesgue measure zero subsets of the reals. Our reformulation does not come from a definition of the Lebesgue measure in terms of an ideal J on
$\omega $
, of the ideal of Lebesgue measure zero subsets of the reals. Our reformulation does not come from a definition of the Lebesgue measure in terms of an ideal J on
![]() $\omega $
, but it is inspired from one combinatorial characterization of measure zero. Details of this new definition are provided in Section 2. We work in the Cantor space
$\omega $
, but it is inspired from one combinatorial characterization of measure zero. Details of this new definition are provided in Section 2. We work in the Cantor space
![]() ${{}^\omega 2}$
for simplicity, but the same reformulations and results can be obtained in other standard Polish spaces with a measure (see Section 7). We denote by
${{}^\omega 2}$
for simplicity, but the same reformulations and results can be obtained in other standard Polish spaces with a measure (see Section 7). We denote by
![]() ${\mathcal {N}}_J$
the collection of null subsets modulo J of
${\mathcal {N}}_J$
the collection of null subsets modulo J of
![]() ${{}^\omega 2}$
. It will be clear that
${{}^\omega 2}$
. It will be clear that
![]() ${\mathcal {N}}_{\mathrm {Fin}}={\mathcal {N}}$
, the ideal of Lebesgue measure subsets of
${\mathcal {N}}_{\mathrm {Fin}}={\mathcal {N}}$
, the ideal of Lebesgue measure subsets of
![]() ${{}^\omega 2}$
, where
${{}^\omega 2}$
, where
![]() ${\mathrm {Fin}}$
denotes the ideal of finite subsets of
${\mathrm {Fin}}$
denotes the ideal of finite subsets of
![]() $\omega $
.
$\omega $
.
We also provide a reformulation of
![]() ${\mathcal {E}}$
, the ideal generated by the
${\mathcal {E}}$
, the ideal generated by the
![]() $F_\sigma $
measure zero subsets of
$F_\sigma $
measure zero subsets of
![]() ${{}^\omega 2}$
, in terms of an ideal J on
${{}^\omega 2}$
, in terms of an ideal J on
![]() $\omega $
, which we denote by
$\omega $
, which we denote by
![]() ${\mathcal {N}}^*_J$
. As expected, we have
${\mathcal {N}}^*_J$
. As expected, we have
![]() ${\mathcal {N}}^*_{\mathrm {Fin}} = {\mathcal {E}}$
.
${\mathcal {N}}^*_{\mathrm {Fin}} = {\mathcal {E}}$
.
We obtain that, for any ideal J on the natural numbers,
![]() ${\mathcal {N}}_J$
and
${\mathcal {N}}_J$
and
![]() ${\mathcal {N}}^*_J$
are actually
${\mathcal {N}}^*_J$
are actually
![]() $\sigma $
-ideals on
$\sigma $
-ideals on
![]() ${{}^\omega 2}$
and that, whenever K is another ideal on
${{}^\omega 2}$
and that, whenever K is another ideal on
![]() $\omega $
and
$\omega $
and
![]() $J\subseteq K$
,
$J\subseteq K$
,
In fact, it will be clear from the definitions that, whenever K is a maximal ideal on
![]() $\omega $
,
$\omega $
,
![]() ${\mathcal {N}}^*_K={\mathcal {N}}_K$
.
${\mathcal {N}}^*_K={\mathcal {N}}_K$
.
Our first set of main results work as interesting characterizations of ideals on
![]() $\omega $
with the Baire property:
$\omega $
with the Baire property:
Theorem A. Let J be an ideal on
![]() $\omega $
. Then, the following statements are equivalent:
$\omega $
. Then, the following statements are equivalent:
-
(i) J has the Baire property.
-
(ii)
 ${\mathcal {N}}_J={\mathcal {N}}$
.
${\mathcal {N}}_J={\mathcal {N}}$
. -
(iii)
 ${\mathcal {N}}^*_J={\mathcal {E}}$
.
${\mathcal {N}}^*_J={\mathcal {E}}$
.
Although no new ideals on the reals are obtained from ideals with the Baire property, we obtain new characterizations of the ideals
![]() ${\mathcal {N}}$
and
${\mathcal {N}}$
and
![]() ${\mathcal {E}}$
. Moreover, ideals without the Baire property offer new ideals on the reals that are worth of research: the previous result can be expanded in connection with
${\mathcal {E}}$
. Moreover, ideals without the Baire property offer new ideals on the reals that are worth of research: the previous result can be expanded in connection with
![]() ${\mathcal {M}}$
, the ideal of meager subsets of
${\mathcal {M}}$
, the ideal of meager subsets of
![]() ${{}^\omega 2}$
.
${{}^\omega 2}$
.
Theorem B. Let J be an ideal on
![]() $\omega $
. Then, the following statements are equivalent:
$\omega $
. Then, the following statements are equivalent:
 $$ \begin{align*} \begin{array}{ll} \mathrm{(i)}\ \ J\ \mbox{does not have the Baire property.}\qquad \qquad & \mathrm{(iv)}\ \ \mbox{No member of}\ {\mathcal{N}}_J\ \mbox{is co-meager}\mbox{.}\\ \mathrm{(ii)}\ \ {\mathcal{N}}_J\subsetneq{\mathcal{N}}\mbox{.} & \mathrm{(v)}\ \ {\mathcal{M}}\cap{\mathcal{N}}\nsubseteq{\mathcal{N}}_J\mbox{.}\\ \mathrm{(iii)}\ \ {\mathcal{E}} \subsetneq {\mathcal{N}}^*_J\mbox{.} & \mathrm{(vi)}\ \ {\mathcal{N}}^*_J\nsubseteq{\mathcal{M}}\mbox{.}\\ \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{ll} \mathrm{(i)}\ \ J\ \mbox{does not have the Baire property.}\qquad \qquad & \mathrm{(iv)}\ \ \mbox{No member of}\ {\mathcal{N}}_J\ \mbox{is co-meager}\mbox{.}\\ \mathrm{(ii)}\ \ {\mathcal{N}}_J\subsetneq{\mathcal{N}}\mbox{.} & \mathrm{(v)}\ \ {\mathcal{M}}\cap{\mathcal{N}}\nsubseteq{\mathcal{N}}_J\mbox{.}\\ \mathrm{(iii)}\ \ {\mathcal{E}} \subsetneq {\mathcal{N}}^*_J\mbox{.} & \mathrm{(vi)}\ \ {\mathcal{N}}^*_J\nsubseteq{\mathcal{M}}\mbox{.}\\ \end{array} \end{align*} $$
Theorems A and B summarize Theorems 2.18, 3.7, and 3.11 and Corollary 3.5. There are two elements providing the proof of these results. The first corresponds to monotonicity results with respect to the well-known Katětov–Blass order
![]() ${\mathrel {\leq _{\mathrm {KB}}}}$
and Rudin–Blass order
${\mathrel {\leq _{\mathrm {KB}}}}$
and Rudin–Blass order
![]() ${\mathrel {\leq _{\mathrm {RB}}}}$
between ideals (Theorem 2.15), and the second is Bartoszyński’s and Scheepers’ game [Reference Bartoszyński and Scheepers5] that characterizes filters (and hence ideals) with the Baire property, which we use to prove many properties of
${\mathrel {\leq _{\mathrm {RB}}}}$
between ideals (Theorem 2.15), and the second is Bartoszyński’s and Scheepers’ game [Reference Bartoszyński and Scheepers5] that characterizes filters (and hence ideals) with the Baire property, which we use to prove many properties of
![]() ${\mathcal {N}}_J$
and
${\mathcal {N}}_J$
and
![]() ${\mathcal {N}}^*_J$
for any ideal J on
${\mathcal {N}}^*_J$
for any ideal J on
![]() $\omega $
without the Baire property, specifically that
$\omega $
without the Baire property, specifically that
![]() ${\mathcal {N}}_J$
cannot contain co-meager subsets of
${\mathcal {N}}_J$
cannot contain co-meager subsets of
![]() ${{}^\omega 2}$
, and that
${{}^\omega 2}$
, and that
![]() ${\mathcal {N}}^*_J$
contains non-meager sets.
${\mathcal {N}}^*_J$
contains non-meager sets.
About the connection between
![]() ${\mathcal {N}}_J$
and
${\mathcal {N}}_J$
and
![]() ${\mathcal {N}}_K$
for different ideals J and K on
${\mathcal {N}}_K$
for different ideals J and K on
![]() $\omega $
, (and likewise for
$\omega $
, (and likewise for
![]() ${\mathcal {N}}^*_J$
and
${\mathcal {N}}^*_J$
and
![]() ${\mathcal {N}}^*_K$
), we discovered a deep connection between these ideals and the notion of nearly coherence of ideals (or filters) on
${\mathcal {N}}^*_K$
), we discovered a deep connection between these ideals and the notion of nearly coherence of ideals (or filters) on
![]() $\omega $
, original from Blass [Reference Blass7]. The ideals J and K are nearly coherent if there is some finite-to-one function
$\omega $
, original from Blass [Reference Blass7]. The ideals J and K are nearly coherent if there is some finite-to-one function
![]() $f\colon \omega \to \omega $
such that
$f\colon \omega \to \omega $
such that
![]() ${\left \{ {y\subseteq \omega } :\, {f^{-1}[y]\in J\cup K} \right \}}$
generates an ideal. We prove that nearly coherence of ideals is characterized as follows:
${\left \{ {y\subseteq \omega } :\, {f^{-1}[y]\in J\cup K} \right \}}$
generates an ideal. We prove that nearly coherence of ideals is characterized as follows:
Theorem C (Theorem 4.10).
Let J and K be ideals on
![]() $\omega $
. Then the following statements are equivalent:
$\omega $
. Then the following statements are equivalent:
-
(i) J and K are nearly coherent.
-
(ii) There is some ideal
 $K'$
such that
$K'$
such that
 ${\mathcal {N}}^*_J\cup {\mathcal {N}}^*_K\subseteq {\mathcal {N}}^*_{K'}\subseteq {\mathcal {N}}_{K'}\subseteq {\mathcal {N}}_J\cap {\mathcal {N}}_K$
.
${\mathcal {N}}^*_J\cup {\mathcal {N}}^*_K\subseteq {\mathcal {N}}^*_{K'}\subseteq {\mathcal {N}}_{K'}\subseteq {\mathcal {N}}_J\cap {\mathcal {N}}_K$
. -
(iii)
 ${\mathcal {N}}^*_J\subseteq {\mathcal {N}}_K$
.
${\mathcal {N}}^*_J\subseteq {\mathcal {N}}_K$
.
This means that, whenever J and K are not nearly coherent, the ideals
![]() ${\mathcal {N}}_J$
and
${\mathcal {N}}_J$
and
![]() ${\mathcal {N}}_K$
are quite different, likewise for
${\mathcal {N}}_K$
are quite different, likewise for
![]() ${\mathcal {N}}^*_J$
and
${\mathcal {N}}^*_J$
and
![]() ${\mathcal {N}}^*_K$
.
${\mathcal {N}}^*_K$
.
Blass and Shelah [Reference Blass and Shelah11] proved that it is consistent with ZFC that any pair of ideals are nearly coherent, which is known as NCF, the principle of nearly coherence of filters. Theorem C implies that, under NCF, there is only one
![]() ${\mathcal {N}}_J$
for maximal ideals J on
${\mathcal {N}}_J$
for maximal ideals J on
![]() $\omega $
. We still do not know whether NCF implies that there is just one
$\omega $
. We still do not know whether NCF implies that there is just one
![]() ${\mathcal {N}}_J$
(or
${\mathcal {N}}_J$
(or
![]() ${\mathcal {N}}^*_J$
) for J without the Baire property. On the other hand, when we assume that there are not nearly coherent ideals (which is consistent with ZFC, e.g., it is valid under CH and in random model, see [Reference Blass7, Section 4]), we can construct a non-meager ideal K on
${\mathcal {N}}^*_J$
) for J without the Baire property. On the other hand, when we assume that there are not nearly coherent ideals (which is consistent with ZFC, e.g., it is valid under CH and in random model, see [Reference Blass7, Section 4]), we can construct a non-meager ideal K on
![]() $\omega $
such that
$\omega $
such that
![]() ${\mathcal {N}}^*_K\neq {\mathcal {N}}_K$
(Lemma 4.11). In contrast with the previous question, we do not know whether ZFC proves the existence of an ideal K without the Baire property such that
${\mathcal {N}}^*_K\neq {\mathcal {N}}_K$
(Lemma 4.11). In contrast with the previous question, we do not know whether ZFC proves the existence of an ideal K without the Baire property such that
![]() ${\mathcal {N}}^*_K\neq {\mathcal {N}}_K$
.
${\mathcal {N}}^*_K\neq {\mathcal {N}}_K$
.
The proof of Theorem C uses Eisworth’s game that characterizes nearly coherence [Reference Eisworth20]. Another element relevant to this proof is the order
![]() ${\mathrel {\leq _{\overline {\mathrm {KB}}}}}$
, which is the dual of the Katětov–Blass order (see Definition 2.14). If J and K are nearly coherent then it is clear that there is some ideal
${\mathrel {\leq _{\overline {\mathrm {KB}}}}}$
, which is the dual of the Katětov–Blass order (see Definition 2.14). If J and K are nearly coherent then it is clear that there is some ideal
![]() $K'$
such that
$K'$
such that
![]() $J,K{\mathrel {\leq _{\overline {\mathrm {KB}}}}} K'$
, but the converse is also true thanks to Theorem C. This equivalence is claimed in [Reference Blass7], but here we present an alternative proof using our new ideals.
$J,K{\mathrel {\leq _{\overline {\mathrm {KB}}}}} K'$
, but the converse is also true thanks to Theorem C. This equivalence is claimed in [Reference Blass7], but here we present an alternative proof using our new ideals.
We also study the cardinal characteristics associated with the ideals
![]() ${\mathcal {N}}_J$
and
${\mathcal {N}}_J$
and
![]() ${\mathcal {N}}^*_J$
, i.e., additivity, covering, uniformity, and cofinality. Recall that
${\mathcal {N}}^*_J$
, i.e., additivity, covering, uniformity, and cofinality. Recall that
![]() ${\mathfrak {s}}$
denotes the splitting number and
${\mathfrak {s}}$
denotes the splitting number and
![]() ${\mathfrak {r}}$
the reaping number.Footnote
1
In ZFC, we can prove the following result.
${\mathfrak {r}}$
the reaping number.Footnote
1
In ZFC, we can prove the following result.
Theorem D. Let J be an ideal on
![]() $\omega $
. With respect to Cichoń’s diagram (see Figure 1):
$\omega $
. With respect to Cichoń’s diagram (see Figure 1):
-
(a)
 ${\mathrm {cov}}({\mathcal {N}})\leq {\mathrm {cov}}({\mathcal {N}}_J) \leq {\mathrm {cov}}({\mathcal {N}}^*_J)\leq {\mathrm {cov}}({\mathcal {E}}) \leq \min \{{\mathrm {cof}}({\mathcal {M}}),{\mathfrak {r}}\}$
and i.e., the coverings of
${\mathrm {cov}}({\mathcal {N}})\leq {\mathrm {cov}}({\mathcal {N}}_J) \leq {\mathrm {cov}}({\mathcal {N}}^*_J)\leq {\mathrm {cov}}({\mathcal {E}}) \leq \min \{{\mathrm {cof}}({\mathcal {M}}),{\mathfrak {r}}\}$
and i.e., the coverings of $$ \begin{align*}\max\{{\mathrm{add}}({\mathcal{M}}),{\mathfrak{s}}\}\leq {\mathrm{non}}({\mathcal{E}})\leq {\mathrm{non}}({\mathcal{N}}^*_J)\leq {\mathrm{non}}({\mathcal{N}}_J) \leq {\mathrm{non}}({\mathcal{N}}),\end{align*} $$
$$ \begin{align*}\max\{{\mathrm{add}}({\mathcal{M}}),{\mathfrak{s}}\}\leq {\mathrm{non}}({\mathcal{E}})\leq {\mathrm{non}}({\mathcal{N}}^*_J)\leq {\mathrm{non}}({\mathcal{N}}_J) \leq {\mathrm{non}}({\mathcal{N}}),\end{align*} $$
 ${\mathcal {N}}_J$
and
${\mathcal {N}}_J$
and
 ${\mathcal {N}}^*_J$
are between
${\mathcal {N}}^*_J$
are between
 ${\mathrm {cov}}({\mathcal {N}})$
and
${\mathrm {cov}}({\mathcal {N}})$
and
 $\min \{{\mathrm {cof}}({\mathcal {M}}),{\mathfrak {r}}\}$
, and their uniformities are between
$\min \{{\mathrm {cof}}({\mathcal {M}}),{\mathfrak {r}}\}$
, and their uniformities are between
 $\min \{{\mathrm {add}}({\mathcal {M}}),{\mathfrak {s}}\}$
and
$\min \{{\mathrm {add}}({\mathcal {M}}),{\mathfrak {s}}\}$
and
 ${\mathrm {non}}({\mathcal {N}})$
.
${\mathrm {non}}({\mathcal {N}})$
.
-
(b) The additivities of
 ${\mathcal {N}}_J$
and
${\mathcal {N}}_J$
and
 ${\mathcal {N}}^*_J$
are between
${\mathcal {N}}^*_J$
are between
 ${\mathrm {add}}({\mathcal {N}})$
and
${\mathrm {add}}({\mathcal {N}})$
and
 ${\mathrm {cov}}({\mathcal {M}})$
, and their cofinalities are between
${\mathrm {cov}}({\mathcal {M}})$
, and their cofinalities are between
 ${\mathrm {non}}({\mathcal {M}})$
and
${\mathrm {non}}({\mathcal {M}})$
and
 ${\mathrm {cof}}({\mathcal {N}})$
.
${\mathrm {cof}}({\mathcal {N}})$
.

Figure 1 Cichoń’s diagram including the cardinal characteristics associated with our ideals,
![]() ${\mathfrak {s}}$
and
${\mathfrak {s}}$
and
![]() ${\mathfrak {r}}$
, as stated in Theorem D.
${\mathfrak {r}}$
, as stated in Theorem D.
The previous theorem summarizes Theorem 5.6 and Corollary 5.13. Item (a) follows directly by the subset relation between the ideals, and also because
![]() ${\mathrm {add}}({\mathcal {E}})={\mathrm {add}}({\mathcal {M}})$
and
${\mathrm {add}}({\mathcal {E}})={\mathrm {add}}({\mathcal {M}})$
and
![]() ${\mathrm {cof}}({\mathcal {E}})={\mathrm {cof}}({\mathcal {M}})$
due to Bartoszyński and Shelah [Reference Bartoszyński and Shelah6]. Results from the latter reference guarantee easily the connections with
${\mathrm {cof}}({\mathcal {E}})={\mathrm {cof}}({\mathcal {M}})$
due to Bartoszyński and Shelah [Reference Bartoszyński and Shelah6]. Results from the latter reference guarantee easily the connections with
![]() ${\mathrm {cov}}({\mathcal {M}})$
and
${\mathrm {cov}}({\mathcal {M}})$
and
![]() ${\mathrm {non}}({\mathcal {M}})$
in (b), but the connections with
${\mathrm {non}}({\mathcal {M}})$
in (b), but the connections with
![]() ${\mathrm {add}}({\mathcal {N}})$
and
${\mathrm {add}}({\mathcal {N}})$
and
![]() ${\mathrm {cof}}({\mathcal {N}})$
require quite some work. To prove this, we define two cardinal characteristics
${\mathrm {cof}}({\mathcal {N}})$
require quite some work. To prove this, we define two cardinal characteristics
![]() ${\mathfrak {b}}_J({{\overline {\Omega }}})$
and
${\mathfrak {b}}_J({{\overline {\Omega }}})$
and
![]() ${\mathfrak {d}}_J({{\overline {\Omega }}})$
. It will not be hard to show that the additivities and cofinalities of
${\mathfrak {d}}_J({{\overline {\Omega }}})$
. It will not be hard to show that the additivities and cofinalities of
![]() ${\mathcal {N}}_J$
and
${\mathcal {N}}_J$
and
![]() ${\mathcal {N}}^*_J$
are between
${\mathcal {N}}^*_J$
are between
![]() ${\mathfrak {b}}_J({{\overline {\Omega }}})$
and
${\mathfrak {b}}_J({{\overline {\Omega }}})$
and
![]() ${\mathfrak {d}}_J({{\overline {\Omega }}})$
(Definition 5.9), and that
${\mathfrak {d}}_J({{\overline {\Omega }}})$
(Definition 5.9), and that
![]() ${\mathfrak {b}}_{\mathrm {Fin}}({{\overline {\Omega }}})\leq {\mathfrak {b}}_J({{\overline {\Omega }}})$
and
${\mathfrak {b}}_{\mathrm {Fin}}({{\overline {\Omega }}})\leq {\mathfrak {b}}_J({{\overline {\Omega }}})$
and
![]() ${\mathfrak {d}}_J({{\overline {\Omega }}})\leq {\mathfrak {d}}_{\mathrm {Fin}}({{\overline {\Omega }}})$
. The real effort is to prove the following new characterization of
${\mathfrak {d}}_J({{\overline {\Omega }}})\leq {\mathfrak {d}}_{\mathrm {Fin}}({{\overline {\Omega }}})$
. The real effort is to prove the following new characterization of
![]() ${\mathrm {add}}({\mathcal {N}})$
and
${\mathrm {add}}({\mathcal {N}})$
and
![]() ${\mathrm {cof}}({\mathcal {N}})$
.
${\mathrm {cof}}({\mathcal {N}})$
.
Theorem E (Theorem 5.12).
![]() ${\mathfrak {b}}_{\mathrm {Fin}}({{\overline {\Omega }}})={\mathrm {add}}({\mathcal {N}})$
and
${\mathfrak {b}}_{\mathrm {Fin}}({{\overline {\Omega }}})={\mathrm {add}}({\mathcal {N}})$
and
![]() ${\mathfrak {d}}_{\mathrm {Fin}}({{\overline {\Omega }}})={\mathrm {cof}}({\mathcal {N}})$
.
${\mathfrak {d}}_{\mathrm {Fin}}({{\overline {\Omega }}})={\mathrm {cof}}({\mathcal {N}})$
.
In terms of inequalities with classical characteristics of the continuum, Theorem D seems to be the most optimal: we also manage to prove that, in most cases, no further inequalities can be proved, not just with the cardinals in Cichoń’s diagram, but with many classical cardinal characteristics of the continuum. We just leave few open questions, for example, whether it is consistent that
![]() ${\mathrm {cov}}({\mathcal {N}}_J)<{\mathrm {add}}({\mathcal {M}})$
(and even smaller than the pseudo-intersection number
${\mathrm {cov}}({\mathcal {N}}_J)<{\mathrm {add}}({\mathcal {M}})$
(and even smaller than the pseudo-intersection number
![]() ${\mathfrak {p}}$
) for some maximal ideal J (likewise for
${\mathfrak {p}}$
) for some maximal ideal J (likewise for
![]() ${\mathrm {cof}}({\mathcal {M}})<{\mathrm {non}}({\mathcal {N}}_J)$
). This is all dealt with in Section 6.
${\mathrm {cof}}({\mathcal {M}})<{\mathrm {non}}({\mathcal {N}}_J)$
). This is all dealt with in Section 6.
Many consistency results supporting the above comes from the forcing model after adding uncountably many Cohen reals.
Theorem F (Theorem 6.4).
Let
![]() $\lambda $
be an uncountable cardinal. After adding
$\lambda $
be an uncountable cardinal. After adding
![]() $\lambda $
-many Cohen reals: for any regular uncountable
$\lambda $
-many Cohen reals: for any regular uncountable
![]() $\kappa \leq \lambda $
there is some (maximal) ideal
$\kappa \leq \lambda $
there is some (maximal) ideal
![]() $J^\kappa $
on
$J^\kappa $
on
![]() $\omega $
such that
$\omega $
such that
![]() ${\mathrm {add}}({\mathcal {N}}_{J^\kappa })={\mathrm {cof}}({\mathcal {N}}_{J^\kappa })=\kappa $
.
${\mathrm {add}}({\mathcal {N}}_{J^\kappa })={\mathrm {cof}}({\mathcal {N}}_{J^\kappa })=\kappa $
.
This shows that there are many different values for the cardinal characteristics associated with different
![]() ${\mathcal {N}}_J$
after adding many Cohen reals. This potentially shows that many of these values can be strictly between
${\mathcal {N}}_J$
after adding many Cohen reals. This potentially shows that many of these values can be strictly between
![]() ${\mathrm {non}}({\mathcal {M}})$
and
${\mathrm {non}}({\mathcal {M}})$
and
![]() ${\mathrm {cov}}({\mathcal {M}})$
because, after adding
${\mathrm {cov}}({\mathcal {M}})$
because, after adding
![]() $\lambda $
-many Cohen reals,
$\lambda $
-many Cohen reals,
![]() ${\mathrm {non}}({\mathcal {M}})=\aleph _1$
and
${\mathrm {non}}({\mathcal {M}})=\aleph _1$
and
![]() $\lambda \leq {\mathrm {cov}}({\mathcal {M}})$
(and
$\lambda \leq {\mathrm {cov}}({\mathcal {M}})$
(and
![]() ${\mathfrak {c}}=\lambda $
when
${\mathfrak {c}}=\lambda $
when
![]() $\lambda ^{\aleph _0}=\lambda $
). See more in Section 6, specifically item (M1). This is inspired in Canjar’s result [Reference Canjar18] stating that, after adding
$\lambda ^{\aleph _0}=\lambda $
). See more in Section 6, specifically item (M1). This is inspired in Canjar’s result [Reference Canjar18] stating that, after adding
![]() $\lambda $
many Cohen reals, for any uncountable regular
$\lambda $
many Cohen reals, for any uncountable regular
![]() $\kappa \leq \lambda $
there is some (maximal) ideal
$\kappa \leq \lambda $
there is some (maximal) ideal
![]() $J^\kappa $
such that
$J^\kappa $
such that
![]() ${\mathfrak {b}}_{J^\kappa }={\mathfrak {d}}_{J^\kappa }=\kappa $
.
${\mathfrak {b}}_{J^\kappa }={\mathfrak {d}}_{J^\kappa }=\kappa $
.
1.1 Structure of the paper
In Section 2 we define
![]() ${\mathcal {N}}_J$
and
${\mathcal {N}}_J$
and
![]() ${\mathcal {N}}^*_J$
, prove their basic properties, the monotonicity with respect to the orders
${\mathcal {N}}^*_J$
, prove their basic properties, the monotonicity with respect to the orders
![]() ${\mathrel {\leq _{\mathrm {KB}}}}$
,
${\mathrel {\leq _{\mathrm {KB}}}}$
,
![]() ${\mathrel {\leq _{\overline {\mathrm {KB}}}}}$
, and
${\mathrel {\leq _{\overline {\mathrm {KB}}}}}$
, and
![]() ${\mathrel {\leq _{\mathrm {RB}}}}$
, and that
${\mathrel {\leq _{\mathrm {RB}}}}$
, and that
![]() ${\mathcal {N}}_J={\mathcal {N}}$
and
${\mathcal {N}}_J={\mathcal {N}}$
and
![]() ${\mathcal {N}}^*_J={\mathcal {E}}$
when J has the Baire property. In Section 3 we deal with ideals without the Baire property and finish to prove Theorems A and B. Section 4 is devoted to our results related to nearly coherence of ideals, specifically with the proof of Theorem C. Section 5 presents ZFC results about the cardinal characteristics associated with our new ideals, mainly the proof of Theorems D and E, and Section 6 deals with the consistency results and Theorem F. Finally, in Section 7, we present discussions and summarize some open questions related to this work.
${\mathcal {N}}^*_J={\mathcal {E}}$
when J has the Baire property. In Section 3 we deal with ideals without the Baire property and finish to prove Theorems A and B. Section 4 is devoted to our results related to nearly coherence of ideals, specifically with the proof of Theorem C. Section 5 presents ZFC results about the cardinal characteristics associated with our new ideals, mainly the proof of Theorems D and E, and Section 6 deals with the consistency results and Theorem F. Finally, in Section 7, we present discussions and summarize some open questions related to this work.
2 Measure zero modulo ideals
We first present some basic notation. In general, by an ideal on M we understand a family
![]() ${J}\subseteq {\mathcal {P}}(M)$
that is hereditary (i.e.,
${J}\subseteq {\mathcal {P}}(M)$
that is hereditary (i.e.,
![]() $a\in {J}$
for any
$a\in {J}$
for any
![]() $a \subseteq b\in {J}$
), closed under finite unions, containing all finite subsets of M and such that
$a \subseteq b\in {J}$
), closed under finite unions, containing all finite subsets of M and such that
![]() $M\notin J$
. Let us emphasize that ideals on
$M\notin J$
. Let us emphasize that ideals on
![]() $\omega $
or on any countable set can not be
$\omega $
or on any countable set can not be
![]() $\sigma $
-ideals. We focus on ideals on
$\sigma $
-ideals. We focus on ideals on
![]() $\omega $
and we use the letters
$\omega $
and we use the letters
![]() ${J}$
and
${J}$
and
![]() ${K}$
exclusively to denote such ideals. For
${K}$
exclusively to denote such ideals. For
![]() $P\subseteq {\mathcal {P}}(M)$
we denote
$P\subseteq {\mathcal {P}}(M)$
we denote
Recall that
![]() ${F}\subseteq {\mathcal {P}}(M)$
is a filter when
${F}\subseteq {\mathcal {P}}(M)$
is a filter when
![]() ${F}^d$
is an ideal. A maximal filter
${F}^d$
is an ideal. A maximal filter
![]() ${U}\subseteq {\mathcal {P}}(M)$
with respect to inclusion is called an ultrafilter. For an ideal
${U}\subseteq {\mathcal {P}}(M)$
with respect to inclusion is called an ultrafilter. For an ideal
![]() ${K}\subseteq {\mathcal {P}}(M)$
we denote
${K}\subseteq {\mathcal {P}}(M)$
we denote
![]() ${K}^{+}={\mathcal {P}}(M)\smallsetminus {K}$
. One can see that
${K}^{+}={\mathcal {P}}(M)\smallsetminus {K}$
. One can see that
![]() $a\in {K}^+$
if and only if
$a\in {K}^+$
if and only if
![]() $M\smallsetminus a\notin {K}^d$
.
$M\smallsetminus a\notin {K}^d$
.
A set
![]() $A\subseteq {\mathcal {P}}(M)$
generates an ideal on M iff it has the so called finite union property, i.e.,
$A\subseteq {\mathcal {P}}(M)$
generates an ideal on M iff it has the so called finite union property, i.e.,
![]() $M\smallsetminus \bigcup C$
is infinite for any finite
$M\smallsetminus \bigcup C$
is infinite for any finite
![]() $C\subseteq A$
. In this case, the ideal generated by A isFootnote
2
$C\subseteq A$
. In this case, the ideal generated by A isFootnote
2
When s and t are functions (or sequences
![]() $s=\langle s_i:\, i\in a\rangle $
and
$s=\langle s_i:\, i\in a\rangle $
and
![]() $t:=\langle t_i:\, i\in b\rangle $
),
$t:=\langle t_i:\, i\in b\rangle $
),
![]() $s\subseteq t$
means that s extends t, i.e.,
$s\subseteq t$
means that s extends t, i.e.,
![]() ${\mathrm {dom}} s\subseteq {\mathrm {dom}} t$
and
${\mathrm {dom}} s\subseteq {\mathrm {dom}} t$
and
![]() $t\upharpoonright {\mathrm {dom}} s=s$
(or,
$t\upharpoonright {\mathrm {dom}} s=s$
(or,
![]() $a\subseteq b$
and
$a\subseteq b$
and
![]() $s_i=t_i$
for all
$s_i=t_i$
for all
![]() $i\in a$
). We denote by
$i\in a$
). We denote by
![]() $\mu $
the Lebesgue measure defined on the Cantor space
$\mu $
the Lebesgue measure defined on the Cantor space
![]() ${}^\omega 2$
, that is, the (completion of the) product measure on
${}^\omega 2$
, that is, the (completion of the) product measure on
![]() ${}^\omega 2=\prod _{n<\omega }2$
where
${}^\omega 2=\prod _{n<\omega }2$
where
![]() $2=\{0,1\}$
is endowed with the probability measure that sets
$2=\{0,1\}$
is endowed with the probability measure that sets
![]() $\{0\}$
of measure
$\{0\}$
of measure
![]() $\frac {1}{2}$
. In fact, for any
$\frac {1}{2}$
. In fact, for any
![]() $s\in 2^{<\omega }$
,
$s\in 2^{<\omega }$
,
![]() $\mu ([s])=2^{-|s|}$
where
$\mu ([s])=2^{-|s|}$
where
![]() $|s|$
denotes the length of s and
$|s|$
denotes the length of s and
![]() $[s]:={\left \{ {x\in {{}^\omega 2}} :\, {s\subseteq x} \right \}}$
. Recall that
$[s]:={\left \{ {x\in {{}^\omega 2}} :\, {s\subseteq x} \right \}}$
. Recall that
![]() ${\left \{ {[s]} :\, {s\in 2^{<\omega }} \right \}}$
is a base of clopen sets of the topology of
${\left \{ {[s]} :\, {s\in 2^{<\omega }} \right \}}$
is a base of clopen sets of the topology of
![]() ${{}^\omega 2}$
. Then
${{}^\omega 2}$
. Then
are
![]() $\sigma $
-ideals, i.e., the union of any countable subset of the ideal belongs to the ideal.
$\sigma $
-ideals, i.e., the union of any countable subset of the ideal belongs to the ideal.
The ideal
![]() ${\mathcal {N}}$
has a combinatorial characterization in terms of clopen sets. To present this, we fix the following terminology. We usually write
${\mathcal {N}}$
has a combinatorial characterization in terms of clopen sets. To present this, we fix the following terminology. We usually write
![]() $\bar {c} :={\left \langle {c_n} :\, {n\in \omega }\right \rangle }$
for sequences of sets.
$\bar {c} :={\left \langle {c_n} :\, {n\in \omega }\right \rangle }$
for sequences of sets.
Definition 2.1. Denote
![]() $\Omega :={\left \{ {c\subseteq {}^\omega 2} :\, {c \mbox { is a~clopen set}} \right \}}$
. For
$\Omega :={\left \{ {c\subseteq {}^\omega 2} :\, {c \mbox { is a~clopen set}} \right \}}$
. For
![]() $\varepsilon \colon \omega \to (0,\infty )$
, consider the set
$\varepsilon \colon \omega \to (0,\infty )$
, consider the set
For each
![]() $\bar {c}\in {}^\omega \Omega $
(or in
$\bar {c}\in {}^\omega \Omega $
(or in
![]() ${}^\omega {\mathcal {P}}(\omega )$
in general) denote
${}^\omega {\mathcal {P}}(\omega )$
in general) denote
 $$ \begin{align*} N(\bar{c}) & :=\bigcap_{m<\omega}\bigcup_{n\geq m}c_n ={\left\{ {x\in {}^\omega2} :\, {|{\left\{ {n\in\omega} :\, {x\in c_n} \right\}}|=\aleph_0} \right\}},\\ N^*(\bar c) & :=\bigcup_{m<\omega}\bigcap_{n\geq m}c_n ={\left\{ {x\in{{}^\omega 2}} :\, {|{\left\{ {n\in\omega} :\, {x\notin c_n} \right\}}|<\aleph_0} \right\}}. \end{align*} $$
$$ \begin{align*} N(\bar{c}) & :=\bigcap_{m<\omega}\bigcup_{n\geq m}c_n ={\left\{ {x\in {}^\omega2} :\, {|{\left\{ {n\in\omega} :\, {x\in c_n} \right\}}|=\aleph_0} \right\}},\\ N^*(\bar c) & :=\bigcup_{m<\omega}\bigcap_{n\geq m}c_n ={\left\{ {x\in{{}^\omega 2}} :\, {|{\left\{ {n\in\omega} :\, {x\notin c_n} \right\}}|<\aleph_0} \right\}}. \end{align*} $$
Fact 2.2 [Reference Bartoszyński and Judah4, Lemma 2.3.10].
Let
![]() $\varepsilon :\omega \to (0,\infty )$
, and assume that
$\varepsilon :\omega \to (0,\infty )$
, and assume that
![]() $\sum _{i\in \omega }\varepsilon _i<\infty $
. Then:
$\sum _{i\in \omega }\varepsilon _i<\infty $
. Then:
-
(a) For any
 $\bar {c}\in \Omega ^*_\varepsilon $
,
$\bar {c}\in \Omega ^*_\varepsilon $
,
 $N(\bar {c})\in \mathcal {N}$
.
$N(\bar {c})\in \mathcal {N}$
. -
(b) For any
 $X\subseteq {}^\omega 2$
,
$X\subseteq {}^\omega 2$
,
 $X\in \mathcal {N}$
iff
$X\in \mathcal {N}$
iff
 $(\exists \, \bar {c}\in \Omega ^*_\varepsilon )\ X\subseteq N(\bar {c})$
.
$(\exists \, \bar {c}\in \Omega ^*_\varepsilon )\ X\subseteq N(\bar {c})$
.
The analog of Fact 2.2 using
![]() $N^*(\bar c)$
becomes the characterization of
$N^*(\bar c)$
becomes the characterization of
![]() ${\mathcal {E}}$
, the
${\mathcal {E}}$
, the
![]() $\sigma $
-ideal generated by the closed measure zero subsets of
$\sigma $
-ideal generated by the closed measure zero subsets of
![]() ${{}^\omega 2}$
.
${{}^\omega 2}$
.
Fact 2.3. Let
![]() $\varepsilon :\omega \to (0,\infty )$
and assume that
$\varepsilon :\omega \to (0,\infty )$
and assume that
![]() $\liminf _{i\to \infty }\varepsilon _i=0$
. Then:
$\liminf _{i\to \infty }\varepsilon _i=0$
. Then:
-
(a) For any
 $\bar {c}\in \Omega ^*_\varepsilon $
,
$\bar {c}\in \Omega ^*_\varepsilon $
,
 $N^*(\bar {c})\in \mathcal {E}$
.
$N^*(\bar {c})\in \mathcal {E}$
. -
(b) For any
 $X\subseteq {}^\omega 2$
,
$X\subseteq {}^\omega 2$
,
 $X\in \mathcal {E}$
iff
$X\in \mathcal {E}$
iff
 $(\exists \, \bar {c}\in \Omega ^*_\varepsilon )\ X\subseteq N^*(\bar {c})$
.
$(\exists \, \bar {c}\in \Omega ^*_\varepsilon )\ X\subseteq N^*(\bar {c})$
.
Proof Item (a) is clear because, for any
![]() $n\in \omega $
,
$n\in \omega $
,
![]() $\bigcap _{m\geq n}c_m$
is closed and, since
$\bigcap _{m\geq n}c_m$
is closed and, since
![]() $\liminf \limits _{i\to \infty }\varepsilon _i=0$
and
$\liminf \limits _{i\to \infty }\varepsilon _i=0$
and
![]() $\bar c\in \Omega ^*_\varepsilon $
, it has measure zero.
$\bar c\in \Omega ^*_\varepsilon $
, it has measure zero.
For (b), the implication
![]() $\Leftarrow $
is clear by (a). To see
$\Leftarrow $
is clear by (a). To see
![]() $\Rightarrow $
, let
$\Rightarrow $
, let
![]() $X\in {\mathcal {E}}$
, i.e.,
$X\in {\mathcal {E}}$
, i.e.,
![]() $X\subseteq \bigcup _{n<\omega }F_n$
for some increasing sequence
$X\subseteq \bigcup _{n<\omega }F_n$
for some increasing sequence
![]() $\langle F_n:\, n<\omega \rangle $
of closed measure zero sets. For each
$\langle F_n:\, n<\omega \rangle $
of closed measure zero sets. For each
![]() $n<\omega $
, we can cover
$n<\omega $
, we can cover
![]() $F_n$
with countably many basic clopen sets
$F_n$
with countably many basic clopen sets
![]() $[s_{n,k}]$
(
$[s_{n,k}]$
(
![]() $k<\omega $
) such that
$k<\omega $
) such that
![]() $\sum \limits _{k<\omega }\mu ([s_{n,k}])<\varepsilon _n$
, but by compactness only finitely many of them cover
$\sum \limits _{k<\omega }\mu ([s_{n,k}])<\varepsilon _n$
, but by compactness only finitely many of them cover
![]() $F_n$
, so
$F_n$
, so
![]() $F_n\subseteq c_n:=\bigcup _{k<m_n}[s_{n,k}]$
for some
$F_n\subseteq c_n:=\bigcup _{k<m_n}[s_{n,k}]$
for some
![]() $m_n<\omega $
, and
$m_n<\omega $
, and
![]() $\mu (c_n)<\varepsilon _n$
. Then
$\mu (c_n)<\varepsilon _n$
. Then
![]() $\bar c:=\langle c_n:\, n<\omega \rangle $
is as required.
$\bar c:=\langle c_n:\, n<\omega \rangle $
is as required.
Motivated by the combinatorial characterization of
![]() ${\mathcal {N}}$
and
${\mathcal {N}}$
and
![]() ${\mathcal {E}}$
presented in Facts 2.2 and 2.3, we introduce a smooth modification of these via ideals on
${\mathcal {E}}$
presented in Facts 2.2 and 2.3, we introduce a smooth modification of these via ideals on
![]() $\omega $
. To start, we fix more terminology and strengthen the previous characterizations.
$\omega $
. To start, we fix more terminology and strengthen the previous characterizations.
Definition 2.4. Denote
![]() ${{\overline {\Omega }}} :={\left \{ {\bar {c}\in {}^\omega \Omega } :\, { N(\bar {c})\in {\mathcal {N}}} \right \}}$
.
${{\overline {\Omega }}} :={\left \{ {\bar {c}\in {}^\omega \Omega } :\, { N(\bar {c})\in {\mathcal {N}}} \right \}}$
.
By Fact 2.2(a) we have that
![]() $\Omega ^*_\varepsilon \subseteq {{\overline {\Omega }}}$
whenever
$\Omega ^*_\varepsilon \subseteq {{\overline {\Omega }}}$
whenever
![]() $\varepsilon \colon \omega \to (0,\infty )$
and
$\varepsilon \colon \omega \to (0,\infty )$
and
![]() $\sum _{i<\omega }\varepsilon _i<\infty $
. Hence, as a direct consequence of Fact 2.2, we obtain the following equivalence.
$\sum _{i<\omega }\varepsilon _i<\infty $
. Hence, as a direct consequence of Fact 2.2, we obtain the following equivalence.
Fact 2.5. For any
![]() $X\subseteq {{}^\omega 2}$
,
$X\subseteq {{}^\omega 2}$
,
![]() $X\in {\mathcal {N}}$
iff
$X\in {\mathcal {N}}$
iff
![]() $X\subseteq N(\bar c)$
for some
$X\subseteq N(\bar c)$
for some
![]() $\bar c\in {{\overline {\Omega }}}$
.
$\bar c\in {{\overline {\Omega }}}$
.
We also have the analogous version of
![]() ${\mathcal {E}}$
. Before stating it, we characterize
${\mathcal {E}}$
. Before stating it, we characterize
![]() ${{\overline {\Omega }}}$
as follows.
${{\overline {\Omega }}}$
as follows.
Lemma 2.6. For any sequence
![]() $\bar c=\langle c_i:\, i<\omega \rangle $
, the following statements are equivalent.
$\bar c=\langle c_i:\, i<\omega \rangle $
, the following statements are equivalent.
-
(i)
 $\bar c\in {{\overline {\Omega }}}$
.
$\bar c\in {{\overline {\Omega }}}$
. -
(ii)
 $(\forall \, \varepsilon \in {\mathbb {Q}}^+)\ (\exists \, N<\omega )\ (\forall \, n\geq N)\ \mu \left (\bigcup _{N\leq i<n}c_i\right )<\varepsilon .$
$(\forall \, \varepsilon \in {\mathbb {Q}}^+)\ (\exists \, N<\omega )\ (\forall \, n\geq N)\ \mu \left (\bigcup _{N\leq i<n}c_i\right )<\varepsilon .$
-
(iii) For any
 $\varepsilon \colon \omega \to (0,\infty )$
there is some interval partition
$\varepsilon \colon \omega \to (0,\infty )$
there is some interval partition
 $\bar I=\langle I_n:\, n<\omega \rangle $
of
$\bar I=\langle I_n:\, n<\omega \rangle $
of
 $\omega $
such that
$\omega $
such that
 $\mu \left (\bigcup _{i\in I_n}c_i\right )<\varepsilon _n$
for all
$\mu \left (\bigcup _{i\in I_n}c_i\right )<\varepsilon _n$
for all
 $n>0$
.
$n>0$
. -
(iv) There is an interval partition
 $\bar I=\langle I_n:\, n<\omega \rangle $
of
$\bar I=\langle I_n:\, n<\omega \rangle $
of
 $\omega $
such that
$\omega $
such that  $$ \begin{align*}\sum_{n<\omega}\mu\left(\bigcup_{i\in I_n}c_i\right)<\infty.\end{align*} $$
$$ \begin{align*}\sum_{n<\omega}\mu\left(\bigcup_{i\in I_n}c_i\right)<\infty.\end{align*} $$
Proof
![]() $\mathrm{(i)} \mathrel \Rightarrow \mathrm{(ii)}$
: Let
$\mathrm{(i)} \mathrel \Rightarrow \mathrm{(ii)}$
: Let
![]() $\varepsilon $
be a positive rational number. Since
$\varepsilon $
be a positive rational number. Since
![]() $\bar c\in {{\overline {\Omega }}}$
,
$\bar c\in {{\overline {\Omega }}}$
,
![]() $\mu (N(\bar c))=0$
, so
$\mu (N(\bar c))=0$
, so
![]() $\lim \limits _{n\to \infty }\mu \left (\bigcup _{i\geq n}c_i\right )=0$
. Then
$\lim \limits _{n\to \infty }\mu \left (\bigcup _{i\geq n}c_i\right )=0$
. Then
![]() $\mu \left (\bigcup _{i\geq N}c_i\right )<\varepsilon $
for some
$\mu \left (\bigcup _{i\geq N}c_i\right )<\varepsilon $
for some
![]() $N<\omega $
, which clearly implies that
$N<\omega $
, which clearly implies that
![]() $\mu \left (\bigcup _{N\leq i<n}c_i\right )<\varepsilon $
for all
$\mu \left (\bigcup _{N\leq i<n}c_i\right )<\varepsilon $
for all
![]() $n\geq N$
.
$n\geq N$
.
![]() $\mathrm{(ii)}\mathrel {\Rightarrow }\mathrm{(iii)}$
: Let
$\mathrm{(ii)}\mathrel {\Rightarrow }\mathrm{(iii)}$
: Let
![]() $\varepsilon \colon \omega \to (0,\infty )$
. Using (ii), by recursion on
$\varepsilon \colon \omega \to (0,\infty )$
. Using (ii), by recursion on
![]() $n<\omega $
we define an increasing sequence
$n<\omega $
we define an increasing sequence
![]() $\langle m_n:\, n<\omega \rangle $
with
$\langle m_n:\, n<\omega \rangle $
with
![]() $m_0=0$
such that
$m_0=0$
such that
![]() $\mu \left (\bigcup _{m_{n+1}\leq i<k}c_i\right )<\varepsilon _{n+1}$
for all
$\mu \left (\bigcup _{m_{n+1}\leq i<k}c_i\right )<\varepsilon _{n+1}$
for all
![]() $k\geq m_{n+1}$
. Then
$k\geq m_{n+1}$
. Then
![]() $I_n:=[m_n,m_{n+1})$
is as required.
$I_n:=[m_n,m_{n+1})$
is as required.
![]() $\mathrm{(iii)}\mathrel {\Rightarrow }\mathrm{(iv)}$
: Apply (iii) to
$\mathrm{(iii)}\mathrel {\Rightarrow }\mathrm{(iv)}$
: Apply (iii) to
![]() $\varepsilon _n:=2^{-n}$
.
$\varepsilon _n:=2^{-n}$
.
![]() $\mathrm{(iv)}\mathrel {\Rightarrow }\mathrm{(i)}$
: Choose
$\mathrm{(iv)}\mathrel {\Rightarrow }\mathrm{(i)}$
: Choose
![]() $\bar I$
as in (iv), and let
$\bar I$
as in (iv), and let
![]() $c^{\prime }_n:=\bigcup _{i\in I_n}c_i$
. It is clear that
$c^{\prime }_n:=\bigcup _{i\in I_n}c_i$
. It is clear that
![]() $N(\bar c)=N(\bar c')$
and
$N(\bar c)=N(\bar c')$
and
![]() $\bar c'\in \Omega ^*_\varepsilon $
where
$\bar c'\in \Omega ^*_\varepsilon $
where
![]() $\varepsilon \colon \omega \to (0,\infty )$
,
$\varepsilon \colon \omega \to (0,\infty )$
,
![]() $\varepsilon _n:=\mu (c^{\prime }_n)+2^{-n}$
. Since
$\varepsilon _n:=\mu (c^{\prime }_n)+2^{-n}$
. Since
![]() $\sum _{n<\omega }\mu (c^{\prime }_n)<\infty $
, by Fact 2.2 we obtain that
$\sum _{n<\omega }\mu (c^{\prime }_n)<\infty $
, by Fact 2.2 we obtain that
![]() $N(\bar c)=N(\bar c')\in {\mathcal {N}}$
. Thus
$N(\bar c)=N(\bar c')\in {\mathcal {N}}$
. Thus
![]() $\bar c\in {{\overline {\Omega }}}$
.
$\bar c\in {{\overline {\Omega }}}$
.
As a consequence of Lemma 2.6(ii), considering
![]() $\Omega $
as a countable discrete space, the fact below immediately follows.
$\Omega $
as a countable discrete space, the fact below immediately follows.
Corollary 2.7. The set
![]() ${{\overline {\Omega }}}$
is Borel in
${{\overline {\Omega }}}$
is Borel in
![]() ${}^\omega \Omega $
.
${}^\omega \Omega $
.
Lemma 2.8. The ideal
![]() ${\mathcal {E}}$
is characterized as follows:
${\mathcal {E}}$
is characterized as follows:
-
(a)
 $N^*(\bar c)\in {\mathcal {E}}$
for any
$N^*(\bar c)\in {\mathcal {E}}$
for any
 $\bar c\in {{\overline {\Omega }}}$
.
$\bar c\in {{\overline {\Omega }}}$
. -
(b) For
 $X\subseteq {{}^\omega 2}$
,
$X\subseteq {{}^\omega 2}$
,
 $X\in {\mathcal {E}}$
iff
$X\in {\mathcal {E}}$
iff
 $(\exists \, \bar c\in {{\overline {\Omega }}})\ X\subseteq N^*(\bar c)$
.
$(\exists \, \bar c\in {{\overline {\Omega }}})\ X\subseteq N^*(\bar c)$
.
Proof (a) is proved similarly as Fact 2.3(a), noting that
![]() $\bar c\in {{\overline {\Omega }}}$
implies that
$\bar c\in {{\overline {\Omega }}}$
implies that
![]() $\lim _{i\to \infty }\mu (c_i)=0$
(by Lemma 2.6(ii)). (b) follows by (a) and Fact 2.3.
$\lim _{i\to \infty }\mu (c_i)=0$
(by Lemma 2.6(ii)). (b) follows by (a) and Fact 2.3.
We use this characterization to introduce the promised generalized versions of
![]() ${\mathcal {N}}$
and
${\mathcal {N}}$
and
![]() ${\mathcal {E}}$
. Consider the ideal
${\mathcal {E}}$
. Consider the ideal
![]() ${\mathrm {Fin}}$
of finite subsets of
${\mathrm {Fin}}$
of finite subsets of
![]() $\omega $
. For
$\omega $
. For
![]() $\bar c\in {}^\omega \Omega $
and
$\bar c\in {}^\omega \Omega $
and
![]() $x\in {{}^\omega 2}$
, note that,
$x\in {{}^\omega 2}$
, note that,
 $$ \begin{align*} x\in N(\bar c) & {\mathrel{\Leftrightarrow}} {\left\{ {n\in\omega} :\, {x\in c_n} \right\}}\in{\mathrm{Fin}}^+,\\ x\in N^*(\bar c) & {\mathrel{\Leftrightarrow}} {\left\{ {n\in\omega} :\, {x\in c_n} \right\}}\in{\mathrm{Fin}}^d. \end{align*} $$
$$ \begin{align*} x\in N(\bar c) & {\mathrel{\Leftrightarrow}} {\left\{ {n\in\omega} :\, {x\in c_n} \right\}}\in{\mathrm{Fin}}^+,\\ x\in N^*(\bar c) & {\mathrel{\Leftrightarrow}} {\left\{ {n\in\omega} :\, {x\in c_n} \right\}}\in{\mathrm{Fin}}^d. \end{align*} $$
Replacing
![]() ${\mathrm {Fin}}$
by an arbitrary ideal on
${\mathrm {Fin}}$
by an arbitrary ideal on
![]() $\omega $
, we obtain the following notion.
$\omega $
, we obtain the following notion.
Definition 2.9. Fix an ideal
![]() ${J}$
on
${J}$
on
![]() $\omega $
. For
$\omega $
. For
![]() $\bar c\in {}^\omega \Omega $
, define
$\bar c\in {}^\omega \Omega $
, define
 $$ \begin{align*} N_{{J}}(\bar{c})&:={\left\{ {x\in {}^\omega2} :\, {{\left\{ n\in\omega :\, x\in c_n \right\}}\in{J}^+} \right\}},\\ N^*_{{J}}(\bar{c})&:={\left\{ {x\in {}^\omega2} :\, {{\left\{ n\in\omega :\, x\in c_n \right\}}\in {J}^d} \right\}}. \end{align*} $$
$$ \begin{align*} N_{{J}}(\bar{c})&:={\left\{ {x\in {}^\omega2} :\, {{\left\{ n\in\omega :\, x\in c_n \right\}}\in{J}^+} \right\}},\\ N^*_{{J}}(\bar{c})&:={\left\{ {x\in {}^\omega2} :\, {{\left\{ n\in\omega :\, x\in c_n \right\}}\in {J}^d} \right\}}. \end{align*} $$
These sets are used to define the families:
We say that the members of
![]() ${\mathcal {N}}_{J}$
have measure zero (or are null) modulo
${\mathcal {N}}_{J}$
have measure zero (or are null) modulo
![]() ${J}$
.
${J}$
.
Due to Fact 2.5 and Lemma 2.8, we obtain
![]() ${\mathcal {N}_{{\mathrm {Fin}}}}={\mathcal {N}}$
and
${\mathcal {N}_{{\mathrm {Fin}}}}={\mathcal {N}}$
and
![]() ${\mathcal {E}}={\mathcal {N}}^*_{{\mathrm {Fin}}}$
. Moreover, one can easily see that, if
${\mathcal {E}}={\mathcal {N}}^*_{{\mathrm {Fin}}}$
. Moreover, one can easily see that, if
![]() ${J}\subseteq {K}$
are ideals on
${J}\subseteq {K}$
are ideals on
![]() $\omega $
, then
$\omega $
, then
In particular, we obtain
Furthermore, if
![]() ${J}$
is a maximal ideal (i.e., its dual
${J}$
is a maximal ideal (i.e., its dual
![]() ${J}^d$
is an ultrafilter), then
${J}^d$
is an ultrafilter), then
![]() ${\mathcal {N}_{{J}}}={\mathcal {N}^*_{J}}$
.
${\mathcal {N}_{{J}}}={\mathcal {N}^*_{J}}$
.
We can prove that, indeed, both
![]() ${\mathcal {N}}_{J}$
and
${\mathcal {N}}_{J}$
and
![]() ${\mathcal {N}}^*_{J}$
are
${\mathcal {N}}^*_{J}$
are
![]() $\sigma $
-ideals on the reals, exactly as the original notions.
$\sigma $
-ideals on the reals, exactly as the original notions.
Lemma 2.10. Let
![]() ${J}$
be an ideal on
${J}$
be an ideal on
![]() $\omega $
. Then both
$\omega $
. Then both
![]() ${\mathcal {N}_{{J}}}$
and
${\mathcal {N}_{{J}}}$
and
![]() ${\mathcal {N}^*_{J}}$
are
${\mathcal {N}^*_{J}}$
are
![]() $\sigma $
-ideals on
$\sigma $
-ideals on
![]() ${{}^\omega 2}$
.
${{}^\omega 2}$
.
Proof Thanks to (2.4), both
![]() ${\mathcal {N}_{{J}}}$
and
${\mathcal {N}_{{J}}}$
and
![]() ${\mathcal {N}^*_{J}}$
contain all finite subsets of
${\mathcal {N}^*_{J}}$
contain all finite subsets of
![]() ${{}^\omega 2}$
and the whole space
${{}^\omega 2}$
and the whole space
![]() ${{}^\omega 2}$
does not belong to them. It is also clear that both families are downwards closed under
${{}^\omega 2}$
does not belong to them. It is also clear that both families are downwards closed under
![]() $\subseteq $
, so it is enough to verify that both
$\subseteq $
, so it is enough to verify that both
![]() ${\mathcal {N}_{{J}}}$
and
${\mathcal {N}_{{J}}}$
and
![]() ${\mathcal {N}^*_{J}}$
are closed under countable unions.
${\mathcal {N}^*_{J}}$
are closed under countable unions.
Consider
![]() $\bar {c}^k \in {{\overline {\Omega }}}$
for each
$\bar {c}^k \in {{\overline {\Omega }}}$
for each
![]() $k\in \omega $
. By recursion, using Lemma 2.6(ii), we define an increasing sequence
$k\in \omega $
. By recursion, using Lemma 2.6(ii), we define an increasing sequence
![]() ${\left \langle {n_l} :\, {l<\omega }\right \rangle }$
of natural numbers such that
${\left \langle {n_l} :\, {l<\omega }\right \rangle }$
of natural numbers such that
![]() $\mu \left (\bigcup _{n\geq n_l}c^k_n\right )<\frac {1}{(l+1)2^l}$
for all
$\mu \left (\bigcup _{n\geq n_l}c^k_n\right )<\frac {1}{(l+1)2^l}$
for all
![]() $k\leq l$
. Let
$k\leq l$
. Let
![]() $I_0:=[0,n_1)$
and
$I_0:=[0,n_1)$
and
![]() $I_l:=[n_l,n_{l+1})$
for
$I_l:=[n_l,n_{l+1})$
for
![]() $l>0$
. Then, we define the sequence
$l>0$
. Then, we define the sequence
![]() $\bar {c}$
by
$\bar {c}$
by
 $$ \begin{align*} c_n = \begin{cases} \bigcup\limits_{k\leq l}c^k_n, & \mbox{if } n\in[n_l,n_{l+1}),\\ \emptyset, & \mbox{if }n<n_0. \end{cases} \end{align*} $$
$$ \begin{align*} c_n = \begin{cases} \bigcup\limits_{k\leq l}c^k_n, & \mbox{if } n\in[n_l,n_{l+1}),\\ \emptyset, & \mbox{if }n<n_0. \end{cases} \end{align*} $$
Finally,
 $$ \begin{align*}\sum_{l<\omega}\mu\left(\bigcup_{n\in I_l}c_n\right)\leq \sum_{l<\omega}\sum_{k\leq l}\mu\left(\bigcup_{n\geq n_l}c^k_n\right)\leq \sum_{l<\omega}\sum_{k\leq l}\frac{1}{(l+1)2^l}=\sum_{l<\omega}\frac{1}{2^l}<\infty,\end{align*} $$
$$ \begin{align*}\sum_{l<\omega}\mu\left(\bigcup_{n\in I_l}c_n\right)\leq \sum_{l<\omega}\sum_{k\leq l}\mu\left(\bigcup_{n\geq n_l}c^k_n\right)\leq \sum_{l<\omega}\sum_{k\leq l}\frac{1}{(l+1)2^l}=\sum_{l<\omega}\frac{1}{2^l}<\infty,\end{align*} $$
so
![]() $\bar c\in {{\overline {\Omega }}}$
by Lemma 2.6(iv). It is clear that
$\bar c\in {{\overline {\Omega }}}$
by Lemma 2.6(iv). It is clear that
![]() $\bigcup _{k\in \omega }N_{J}(\bar {c}^k)\subseteq N_{J}(\bar {c})$
and
$\bigcup _{k\in \omega }N_{J}(\bar {c}^k)\subseteq N_{J}(\bar {c})$
and
![]() $\bigcup _{k\in \omega }N^*_{J}(\bar {c}^k)\subseteq N^*_{J}(\bar {c})$
.
$\bigcup _{k\in \omega }N^*_{J}(\bar {c}^k)\subseteq N^*_{J}(\bar {c})$
.
Remark 2.11. The following alternative definition does not bring anything new: Let
![]() ${{\overline {\Omega }}}_0$
be the set of countable sequences
${{\overline {\Omega }}}_0$
be the set of countable sequences
![]() $\bar a=\langle a_n:n<\omega \rangle $
of open subsets of
$\bar a=\langle a_n:n<\omega \rangle $
of open subsets of
![]() ${}^\omega 2$
such that
${}^\omega 2$
such that
![]() $N(\bar a)\in {\mathcal {N}}$
. Define
$N(\bar a)\in {\mathcal {N}}$
. Define
![]() $N_{J}(\bar {a})$
similarly, and
$N_{J}(\bar {a})$
similarly, and
![]() ${\mathcal {N}}^0_{J}$
as the family of subsets of
${\mathcal {N}}^0_{J}$
as the family of subsets of
![]() ${}^\omega 2$
that are contained in some set of the form
${}^\omega 2$
that are contained in some set of the form
![]() $N_{J}(\bar a)$
for some
$N_{J}(\bar a)$
for some
![]() $\bar a\in {{\overline {\Omega }}}_0$
. Define
$\bar a\in {{\overline {\Omega }}}_0$
. Define
![]() ${\mathcal {N}}^{*0}_{J}$
analogously. It is not hard to show that
${\mathcal {N}}^{*0}_{J}$
analogously. It is not hard to show that
![]() ${\mathcal {N}}^{*0}_{J}={\mathcal {N}}^0_{J}={\mathcal {N}}$
. The inclusions
${\mathcal {N}}^{*0}_{J}={\mathcal {N}}^0_{J}={\mathcal {N}}$
. The inclusions
![]() ${\mathcal {N}}^{*0}_{J}\subseteq {\mathcal {N}}^0_{J}\subseteq {\mathcal {N}}$
are clear; to see
${\mathcal {N}}^{*0}_{J}\subseteq {\mathcal {N}}^0_{J}\subseteq {\mathcal {N}}$
are clear; to see
![]() ${\mathcal {N}}\subseteq {\mathcal {N}}^{*0}_{J}$
, if
${\mathcal {N}}\subseteq {\mathcal {N}}^{*0}_{J}$
, if
![]() $B\in {\mathcal {N}}$
, then we can find some
$B\in {\mathcal {N}}$
, then we can find some
![]() $\bar a\in {{\overline {\Omega }}}_0$
such that
$\bar a\in {{\overline {\Omega }}}_0$
such that
![]() $B\subseteq \bigcap _{n\in \omega }a_n$
and
$B\subseteq \bigcap _{n\in \omega }a_n$
and
![]() $\mu (a_n)<2^{-n}$
, so it is clear that
$\mu (a_n)<2^{-n}$
, so it is clear that
![]() $B\subseteq N^*_{J}(\bar a)$
. For this reason, it is uninteresting to consider sequences of open sets instead of clopen sets.
$B\subseteq N^*_{J}(\bar a)$
. For this reason, it is uninteresting to consider sequences of open sets instead of clopen sets.
Remark 2.12. We expand our discussion by allowing ideals on an arbitrary infinite countable set W instead of
![]() $\omega $
. Namely, for
$\omega $
. Namely, for
![]() $\bar c \in {}^W \Omega $
(or in
$\bar c \in {}^W \Omega $
(or in
![]() ${}^W {\mathcal {P}}({{}^\omega 2})$
), we define
${}^W {\mathcal {P}}({{}^\omega 2})$
), we define
![]() $N_J(\bar c)$
and
$N_J(\bar c)$
and
![]() $N^*_J(\bar c)$
similar to Definition 2.9,
$N^*_J(\bar c)$
similar to Definition 2.9,
![]() ${\mathrm {Fin}}(W)$
as the ideal of finite subsets of W,
${\mathrm {Fin}}(W)$
as the ideal of finite subsets of W,
and
![]() ${\mathcal {N}}_J$
and
${\mathcal {N}}_J$
and
![]() ${\mathcal {N}}^*_J$
as in (2.1) and (2.2), respectively. We need this expansion to allow ideals obtained by operations as in Example 2.13.
${\mathcal {N}}^*_J$
as in (2.1) and (2.2), respectively. We need this expansion to allow ideals obtained by operations as in Example 2.13.
Using a one-to-one enumeration
![]() $W={\left \{ {w_n} :\, {n<\omega } \right \}}$
by Lemma 2.6 we get that, for
$W={\left \{ {w_n} :\, {n<\omega } \right \}}$
by Lemma 2.6 we get that, for
![]() $\bar c\in {}^W \Omega $
,
$\bar c\in {}^W \Omega $
,
 $$ \begin{align} &\bar c\in {{\overline{\Omega}}}(W) \mbox{ iff, } \\ &\mbox{for any }\varepsilon>0 \mbox{, there is some finite set }a\subseteq W\mbox{ such that }\mu\left(\bigcup_{n\in W\smallsetminus a} c_n\right)<\varepsilon.\nonumber \end{align} $$
$$ \begin{align} &\bar c\in {{\overline{\Omega}}}(W) \mbox{ iff, } \\ &\mbox{for any }\varepsilon>0 \mbox{, there is some finite set }a\subseteq W\mbox{ such that }\mu\left(\bigcup_{n\in W\smallsetminus a} c_n\right)<\varepsilon.\nonumber \end{align} $$
In fact, considering the bijection
![]() $f\colon \omega \to W$
defined by
$f\colon \omega \to W$
defined by
![]() $f(n):=w_n$
for
$f(n):=w_n$
for
![]() $n<\omega $
, and the ideal
$n<\omega $
, and the ideal
![]() $J':={\left \{ {f^{-1}[a]} :\, {a\in J} \right \}}$
(which is isomorphic to J), we obtain
$J':={\left \{ {f^{-1}[a]} :\, {a\in J} \right \}}$
(which is isomorphic to J), we obtain
![]() ${\mathcal {N}}_J = {\mathcal {N}}_{J'}$
and
${\mathcal {N}}_J = {\mathcal {N}}_{J'}$
and
![]() ${\mathcal {N}}^*_J ={\mathcal {N}}^*_{J'}$
. As a consequence,
${\mathcal {N}}^*_J ={\mathcal {N}}^*_{J'}$
. As a consequence,
![]() ${\mathcal {N}}_{{\mathrm {Fin}}(W)}={\mathcal {N}}_{\mathrm {Fin}}={\mathcal {N}}$
and
${\mathcal {N}}_{{\mathrm {Fin}}(W)}={\mathcal {N}}_{\mathrm {Fin}}={\mathcal {N}}$
and
![]() ${\mathcal {N}}^*_{{\mathrm {Fin}}(W)}={\mathcal {N}}^*_{{\mathrm {Fin}}}={\mathcal {E}}$
.
${\mathcal {N}}^*_{{\mathrm {Fin}}(W)}={\mathcal {N}}^*_{{\mathrm {Fin}}}={\mathcal {E}}$
.
Example 2.13. Consider
![]() $\omega ={\mathbb {N}}_1\cup {\mathbb {N}}_2$
as a disjoint union of infinite sets, let
$\omega ={\mathbb {N}}_1\cup {\mathbb {N}}_2$
as a disjoint union of infinite sets, let
![]() $J_1$
be an ideal on
$J_1$
be an ideal on
![]() ${\mathbb {N}}_1$
and
${\mathbb {N}}_1$
and
![]() $J_2$
an ideal on
$J_2$
an ideal on
![]() ${\mathbb {N}}_2$
. Recall the ideal
${\mathbb {N}}_2$
. Recall the ideal
Note that:
-
(1)
 $\bar c\in {{\overline {\Omega }}}$
iff
$\bar c\in {{\overline {\Omega }}}$
iff
 $\bar c\upharpoonright {\mathbb {N}}_1\in {{\overline {\Omega }}}({\mathbb {N}}_1)$
and
$\bar c\upharpoonright {\mathbb {N}}_1\in {{\overline {\Omega }}}({\mathbb {N}}_1)$
and
 $\bar c\upharpoonright {\mathbb {N}}_2\in {{\overline {\Omega }}}({\mathbb {N}}_2)$
.
$\bar c\upharpoonright {\mathbb {N}}_2\in {{\overline {\Omega }}}({\mathbb {N}}_2)$
. -
(2) For
 $\bar c\in {{\overline {\Omega }}}$
,
$\bar c\in {{\overline {\Omega }}}$
,  $$ \begin{align*} N_{J_1\oplus J_2}(\bar c) & =N_{J_1}(\bar c\upharpoonright{\mathbb{N}}_1)\cup N_{J_2}(\bar c\upharpoonright{\mathbb{N}}_2)) \mbox{ and }\\ N^*_{J_1\oplus J_2}(\bar c) & =N^*_{J_1}(\bar c\upharpoonright{\mathbb{N}}_1)\cap N^*_{J_2}(\bar c\upharpoonright{\mathbb{N}}_2). \end{align*} $$
$$ \begin{align*} N_{J_1\oplus J_2}(\bar c) & =N_{J_1}(\bar c\upharpoonright{\mathbb{N}}_1)\cup N_{J_2}(\bar c\upharpoonright{\mathbb{N}}_2)) \mbox{ and }\\ N^*_{J_1\oplus J_2}(\bar c) & =N^*_{J_1}(\bar c\upharpoonright{\mathbb{N}}_1)\cap N^*_{J_2}(\bar c\upharpoonright{\mathbb{N}}_2). \end{align*} $$
As a consequence:
-
(3)
 ${\mathcal {N}}_{J_1\oplus J_2}$
is the ideal generated by
${\mathcal {N}}_{J_1\oplus J_2}$
is the ideal generated by
 ${\mathcal {N}}_{J_1}\cup {\mathcal {N}}_{J_2}$
, in fact
${\mathcal {N}}_{J_1}\cup {\mathcal {N}}_{J_2}$
, in fact  $$ \begin{align*}{\mathcal{N}}_{J_1\oplus J_2}={\left\{ {X\cup Y} :\, {X\in {\mathcal{N}}_{J_1} \mbox{ and } Y\in {\mathcal{N}}_{J_2} } \right\}}.\end{align*} $$
$$ \begin{align*}{\mathcal{N}}_{J_1\oplus J_2}={\left\{ {X\cup Y} :\, {X\in {\mathcal{N}}_{J_1} \mbox{ and } Y\in {\mathcal{N}}_{J_2} } \right\}}.\end{align*} $$
-
(4)
 ${\mathcal {N}}^*_{J_1\oplus J_2}={\mathcal {N}}^*_{J_1}\cap {\mathcal {N}}^*_{J_2}$
.
${\mathcal {N}}^*_{J_1\oplus J_2}={\mathcal {N}}^*_{J_1}\cap {\mathcal {N}}^*_{J_2}$
.
The inclusion
![]() $\subseteq $
in both (3) and (4) follows from (2); the converse follows by the fact that, whenever
$\subseteq $
in both (3) and (4) follows from (2); the converse follows by the fact that, whenever
![]() $\bar c^1\in {{\overline {\Omega }}}({\mathbb {N}}_1)$
and
$\bar c^1\in {{\overline {\Omega }}}({\mathbb {N}}_1)$
and
![]() $\bar c^2\in {{\overline {\Omega }}}({\mathbb {N}}_2)$
,
$\bar c^2\in {{\overline {\Omega }}}({\mathbb {N}}_2)$
,
![]() $\bar c\in {{\overline {\Omega }}}$
where
$\bar c\in {{\overline {\Omega }}}$
where
![]() $\bar c = \bar c^1\cup \bar c^2$
, i.e.,
$\bar c = \bar c^1\cup \bar c^2$
, i.e.,
![]() $\bar c=\langle c_n:\, n<\omega \rangle $
such that
$\bar c=\langle c_n:\, n<\omega \rangle $
such that
![]() $c_n:=c^i_n$
when
$c_n:=c^i_n$
when
![]() $n\in {\mathbb {N}}_i$
(
$n\in {\mathbb {N}}_i$
(
![]() $i\in \{1,2\}$
), and
$i\in \{1,2\}$
), and
 $$ \begin{align*} N_{J_1\oplus J_2}(\bar c) & =N_{J_1}(\bar c^1)\cup N_{J_2}(\bar c^2)) \mbox{ and }\\ N^*_{J_1\oplus J_2}(\bar c) & =N^*_{J_1}(\bar c^1)\cap N^*_{J_2}(\bar c^2), \end{align*} $$
$$ \begin{align*} N_{J_1\oplus J_2}(\bar c) & =N_{J_1}(\bar c^1)\cup N_{J_2}(\bar c^2)) \mbox{ and }\\ N^*_{J_1\oplus J_2}(\bar c) & =N^*_{J_1}(\bar c^1)\cap N^*_{J_2}(\bar c^2), \end{align*} $$
which follow by (1) and (2) because
![]() $\bar c^i=\bar c\upharpoonright {\mathbb {N}}_i$
for
$\bar c^i=\bar c\upharpoonright {\mathbb {N}}_i$
for
![]() $i\in \{1,2\}$
.
$i\in \{1,2\}$
.
By allowing
![]() ${\mathcal {P}}(\omega )$
instead of an ideal,
${\mathcal {P}}(\omega )$
instead of an ideal,
![]() $N_{{\mathcal {P}}(\omega )}(\bar c)=\emptyset $
and
$N_{{\mathcal {P}}(\omega )}(\bar c)=\emptyset $
and
![]() $N^*_{{\mathcal {P}}(\omega )}(\bar c)={{}^\omega 2}$
. Since
$N^*_{{\mathcal {P}}(\omega )}(\bar c)={{}^\omega 2}$
. Since
is an ideal, for any
![]() $\bar c\in {{\overline {\Omega }}}$
, we obtain
$\bar c\in {{\overline {\Omega }}}$
, we obtain
![]() $N_{J_1\oplus {\mathcal {P}}({\mathbb {N}}_2)}(\bar c) =N_{J_1}(\bar c\upharpoonright {\mathbb {N}}_1)$
and
$N_{J_1\oplus {\mathcal {P}}({\mathbb {N}}_2)}(\bar c) =N_{J_1}(\bar c\upharpoonright {\mathbb {N}}_1)$
and
![]() $N_{J_1\oplus {\mathcal {P}}({\mathbb {N}}_2)}^*(\bar c) =N_{J_1}^*(\bar c\upharpoonright {\mathbb {N}}_1)$
by (2). Therefore,
$N_{J_1\oplus {\mathcal {P}}({\mathbb {N}}_2)}^*(\bar c) =N_{J_1}^*(\bar c\upharpoonright {\mathbb {N}}_1)$
by (2). Therefore,
![]() ${\mathcal {N}}_{J_1\oplus {\mathcal {P}}({\mathbb {N}}_2)}={\mathcal {N}}_{J_1}$
and
${\mathcal {N}}_{J_1\oplus {\mathcal {P}}({\mathbb {N}}_2)}={\mathcal {N}}_{J_1}$
and
![]() ${\mathcal {N}}^*_{J_1\oplus {\mathcal {P}}({\mathbb {N}}_2)}={\mathcal {N}}^*_{J_1}$
. Similar conclusions are valid for
${\mathcal {N}}^*_{J_1\oplus {\mathcal {P}}({\mathbb {N}}_2)}={\mathcal {N}}^*_{J_1}$
. Similar conclusions are valid for
![]() ${\mathcal {P}}({\mathbb {N}}_1)\oplus J_2$
.
${\mathcal {P}}({\mathbb {N}}_1)\oplus J_2$
.
We now review the following classical orders on ideals.
Definition 2.14. Let
![]() $M_1$
and
$M_1$
and
![]() $M_2$
be infinite sets,
$M_2$
be infinite sets,
![]() ${K}_1\subseteq {\mathcal {P}}(M_1)$
and
${K}_1\subseteq {\mathcal {P}}(M_1)$
and
![]() ${K}_2\subseteq {\mathcal {P}}(M_2)$
. If
${K}_2\subseteq {\mathcal {P}}(M_2)$
. If
![]() $\varphi \colon M_2\to M_1$
, the projection of
$\varphi \colon M_2\to M_1$
, the projection of
![]() ${K}_2$
under
${K}_2$
under
![]() $\varphi $
is the family
$\varphi $
is the family
We write
![]() ${K}_1\leq _{\varphi }{K}_2$
when
${K}_1\leq _{\varphi }{K}_2$
when
![]() ${K}_1\subseteq \varphi ^{\to }({K}_2)$
, i.e.,
${K}_1\subseteq \varphi ^{\to }({K}_2)$
, i.e.,
![]() $\varphi ^{-1}(I)\in {K}_2$
for any
$\varphi ^{-1}(I)\in {K}_2$
for any
![]() $I\in {K}_1$
.
$I\in {K}_1$
.
-
(1) [Reference Blass7, Reference Katětov26] The Katětov–Blass order is defined by
 ${K}_1\leq _{\mathrm{KB}}{K}_2$
iff there is a finite-to-one function
${K}_1\leq _{\mathrm{KB}}{K}_2$
iff there is a finite-to-one function
 $\varphi \colon M_2\to M_1$
such that
$\varphi \colon M_2\to M_1$
such that
 $I\in {K}_1$
implies
$I\in {K}_1$
implies
 $\varphi ^{-1}(I)\in {K}_2$
, i.e.,
$\varphi ^{-1}(I)\in {K}_2$
, i.e.,
 ${K}_1\subseteq \varphi ^{\to }({K}_2)$
.
${K}_1\subseteq \varphi ^{\to }({K}_2)$
. -
(2) [Reference Blass7, Reference Laflamme and Zhu31] The Rudin–Blass order is defined by
 ${K}_1\leq _{\mathrm{RB}}{K}_2$
iff there is a finite-to-one function
${K}_1\leq _{\mathrm{RB}}{K}_2$
iff there is a finite-to-one function
 $\varphi \colon M_2\to M_1$
such that
$\varphi \colon M_2\to M_1$
such that
 $I\in {K}_1$
if and only if
$I\in {K}_1$
if and only if
 $\varphi ^{-1}(I)\in {K}_2$
, i.e.,
$\varphi ^{-1}(I)\in {K}_2$
, i.e.,
 $\varphi ^{\to }({K}_2)={K}_1$
.
$\varphi ^{\to }({K}_2)={K}_1$
. -
(3) We also consider the “dual” of the Katětov–Blass order:
 $K_1{\mathrel {\leq _{\overline {\mathrm {KB}}}}} K_2$
iff there is some finite-to-one function
$K_1{\mathrel {\leq _{\overline {\mathrm {KB}}}}} K_2$
iff there is some finite-to-one function
 $\varphi \colon M_1\to M_2$
such that
$\varphi \colon M_1\to M_2$
such that
 $\varphi ^\to (K_1)\subseteq K_2$
.
$\varphi ^\to (K_1)\subseteq K_2$
.
Recall that the relations
![]() ${\mathrel {\leq _{\mathrm {KB}}}}$
and
${\mathrel {\leq _{\mathrm {KB}}}}$
and
![]() ${\mathrel {\leq _{\mathrm {RB}}}}$
are reflexive and transitive, and it can be proved easily that
${\mathrel {\leq _{\mathrm {RB}}}}$
are reflexive and transitive, and it can be proved easily that
![]() ${\mathrel {\leq _{\overline {\mathrm {KB}}}}}$
also has these properties.
${\mathrel {\leq _{\overline {\mathrm {KB}}}}}$
also has these properties.
Note that
![]() $K_1{\mathrel {\leq _{\mathrm {RB}}}} K_2$
implies
$K_1{\mathrel {\leq _{\mathrm {RB}}}} K_2$
implies
![]() $K_1{\mathrel {\leq _{\mathrm {KB}}}} K_2$
and
$K_1{\mathrel {\leq _{\mathrm {KB}}}} K_2$
and
![]() $K_2{\mathrel {\leq _{\overline {\mathrm {KB}}}}} K_1$
. Also recall that
$K_2{\mathrel {\leq _{\overline {\mathrm {KB}}}}} K_1$
. Also recall that
![]() $K_1\subseteq K_2$
implies
$K_1\subseteq K_2$
implies
![]() $K_1{\mathrel {\leq _{\mathrm {KB}}}} K_2$
and
$K_1{\mathrel {\leq _{\mathrm {KB}}}} K_2$
and
![]() $K_1{\mathrel {\leq _{\overline {\mathrm {KB}}}}} K_2$
(using the identity function).
$K_1{\mathrel {\leq _{\overline {\mathrm {KB}}}}} K_2$
(using the identity function).
Recall that, if
![]() ${K}_2$
is an ideal on
${K}_2$
is an ideal on
![]() $M_2$
, then
$M_2$
, then
![]() $\varphi ^{\to }({K}_2)$
is downwards closed under
$\varphi ^{\to }({K}_2)$
is downwards closed under
![]() $\subseteq $
and closed under finite unions, and
$\subseteq $
and closed under finite unions, and
![]() $M_1\not \in \varphi ^{\to }({K}_2)$
. If
$M_1\not \in \varphi ^{\to }({K}_2)$
. If
![]() $\varphi $
is in addition finite-to-one then
$\varphi $
is in addition finite-to-one then
![]() $\varphi ^{\to }({K}_2)$
is an ideal.
$\varphi ^{\to }({K}_2)$
is an ideal.
We show that our defined
![]() $\sigma $
-ideals behave well under the previous orders. In fact, this is a somewhat expected result that can usually be obtained for many well-known objects in topology. For example, given an ideal J on
$\sigma $
-ideals behave well under the previous orders. In fact, this is a somewhat expected result that can usually be obtained for many well-known objects in topology. For example, given an ideal J on
![]() $\omega $
, consider the relation
$\omega $
, consider the relation
![]() $\leq ^J$
on
$\leq ^J$
on
![]() ${{}^\omega \omega }$
defined by
${{}^\omega \omega }$
defined by
![]() $x\leq ^J y$
iff
$x\leq ^J y$
iff
![]() ${\left \{ {n<\omega } :\, {x(n) \nleq y(n)} \right \}}\in J$
, and define the cardinal characteristics
${\left \{ {n<\omega } :\, {x(n) \nleq y(n)} \right \}}\in J$
, and define the cardinal characteristics
 $$ \begin{align*} {\mathfrak{b}}_J & := \min{\left\{ {|F|} :\, {F\subseteq{{}^\omega \omega},\ \neg(\exists\, y\in{{}^\omega \omega})\ (\forall\, x\in F)\ x\leq^J y} \right\}},\\ {\mathfrak{d}}_J & := \min{\left\{ {|D|} :\, {D\subseteq{{}^\omega \omega},\ (\forall\, x\in{{}^\omega \omega})\ (\exists\, y\in D)\ x\leq^J y} \right\}}. \end{align*} $$
$$ \begin{align*} {\mathfrak{b}}_J & := \min{\left\{ {|F|} :\, {F\subseteq{{}^\omega \omega},\ \neg(\exists\, y\in{{}^\omega \omega})\ (\forall\, x\in F)\ x\leq^J y} \right\}},\\ {\mathfrak{d}}_J & := \min{\left\{ {|D|} :\, {D\subseteq{{}^\omega \omega},\ (\forall\, x\in{{}^\omega \omega})\ (\exists\, y\in D)\ x\leq^J y} \right\}}. \end{align*} $$
It is known from [Reference Farkas and Soukup21] that:
-
(1) If
 $K{\mathrel {\leq _{\mathrm {KB}}}} J$
, then
$K{\mathrel {\leq _{\mathrm {KB}}}} J$
, then
 ${\mathfrak {b}}_K\leq {\mathfrak {b}}_J$
and
${\mathfrak {b}}_K\leq {\mathfrak {b}}_J$
and
 ${\mathfrak {d}}_J\leq {\mathfrak {d}}_K$
.
${\mathfrak {d}}_J\leq {\mathfrak {d}}_K$
. -
(2) If
 $K {\mathrel {\leq _{\overline {\mathrm {KB}}}}} J$
, then
$K {\mathrel {\leq _{\overline {\mathrm {KB}}}}} J$
, then
 ${\mathfrak {b}}_K\leq {\mathfrak {b}}_J$
and
${\mathfrak {b}}_K\leq {\mathfrak {b}}_J$
and
 ${\mathfrak {d}}_J\leq {\mathfrak {d}}_K$
.
${\mathfrak {d}}_J\leq {\mathfrak {d}}_K$
. -
(3) If
 $K{\mathrel {\leq _{\mathrm {RB}}}} J$
, then
$K{\mathrel {\leq _{\mathrm {RB}}}} J$
, then
 ${\mathfrak {b}}_I={\mathfrak {b}}_J$
and
${\mathfrak {b}}_I={\mathfrak {b}}_J$
and
 ${\mathfrak {d}}_I={\mathfrak {d}}_J$
.
${\mathfrak {d}}_I={\mathfrak {d}}_J$
.
We present another similar example in Theorem 5.11.Footnote 3
Theorem 2.15. Let
![]() ${\mathbb {N}}_1$
and
${\mathbb {N}}_1$
and
![]() ${\mathbb {N}}_2$
be countable infinite sets,
${\mathbb {N}}_2$
be countable infinite sets,
![]() ${J}$
an ideal on
${J}$
an ideal on
![]() ${\mathbb {N}}_1$
and let
${\mathbb {N}}_1$
and let
![]() ${K}$
be an ideal on
${K}$
be an ideal on
![]() ${\mathbb {N}}_2$
. Then:
${\mathbb {N}}_2$
. Then:
-
(a) If
 ${K}{\mathrel {\leq _{\mathrm {KB}}}} {J}$
, then
${K}{\mathrel {\leq _{\mathrm {KB}}}} {J}$
, then
 ${\mathcal {N}}^*_{K}\subseteq {\mathcal {N}}^*_{J}$
and
${\mathcal {N}}^*_{K}\subseteq {\mathcal {N}}^*_{J}$
and
 ${\mathcal {N}}_{J}\subseteq {\mathcal {N}}_{K}$
.
${\mathcal {N}}_{J}\subseteq {\mathcal {N}}_{K}$
. -
(b) If
 $K{\mathrel {\leq _{\overline {\mathrm {KB}}}}} J$
, then
$K{\mathrel {\leq _{\overline {\mathrm {KB}}}}} J$
, then
 ${\mathcal {N}}^*_K\subseteq {\mathcal {N}}^*_J$
and
${\mathcal {N}}^*_K\subseteq {\mathcal {N}}^*_J$
and
 ${\mathcal {N}}_J\subseteq {\mathcal {N}}_K$
.
${\mathcal {N}}_J\subseteq {\mathcal {N}}_K$
. -
(c) If
 ${K}{\mathrel {\leq _{\mathrm {RB}}}} {J}$
, then
${K}{\mathrel {\leq _{\mathrm {RB}}}} {J}$
, then
 ${\mathcal {N}}^*_{J}={\mathcal {N}}^*_{K}$
and
${\mathcal {N}}^*_{J}={\mathcal {N}}^*_{K}$
and
 ${\mathcal {N}}_{J}={\mathcal {N}}_{K}$
.
${\mathcal {N}}_{J}={\mathcal {N}}_{K}$
.
Proof Without loss of generality, we may assume
![]() ${\mathbb {N}}_1={\mathbb {N}}_2=\omega $
in this proof. Fix a finite-to-one function
${\mathbb {N}}_1={\mathbb {N}}_2=\omega $
in this proof. Fix a finite-to-one function
![]() $f\colon \omega \to \omega $
and let
$f\colon \omega \to \omega $
and let
![]() $I_n:=f^{-1}[\{n\}]$
for any
$I_n:=f^{-1}[\{n\}]$
for any
![]() $n\in \omega $
. Given
$n\in \omega $
. Given
![]() $\bar c\in {{\overline {\Omega }}}$
we define sequences
$\bar c\in {{\overline {\Omega }}}$
we define sequences
![]() $\bar c'$
and
$\bar c'$
and
![]() $\bar c^-$
by
$\bar c^-$
by
![]() $c^{\prime }_n:=\bigcup _{k\in I_n}c_k$
and
$c^{\prime }_n:=\bigcup _{k\in I_n}c_k$
and
![]() $c^-_k:= c_{f(k)}$
. Since
$c^-_k:= c_{f(k)}$
. Since
![]() $N(\bar c')= N(\bar c)$
and
$N(\bar c')= N(\bar c)$
and
![]() $N(\bar c^-)\subseteq N(\bar c)$
, we have that
$N(\bar c^-)\subseteq N(\bar c)$
, we have that
![]() $\bar c',\bar c^- \in {{\overline {\Omega }}}$
.
$\bar c',\bar c^- \in {{\overline {\Omega }}}$
.
It is enough to show:
-
(i)
 $K\subseteq f^\to (J)$
implies
$K\subseteq f^\to (J)$
implies
 $N^*_K(\bar c) \subseteq N^*_J(\bar c^-)$
and
$N^*_K(\bar c) \subseteq N^*_J(\bar c^-)$
and
 $N_J(\bar c) \subseteq N_K(\bar c')$
, and
$N_J(\bar c) \subseteq N_K(\bar c')$
, and -
(ii)
 $f^\to (K)\subseteq J$
implies
$f^\to (K)\subseteq J$
implies
 $N^*_K(\bar c)\subseteq N^*_J(\bar c')$
and
$N^*_K(\bar c)\subseteq N^*_J(\bar c')$
and
 $N_J(\bar c)\subseteq N_K(\bar c^-)$
.
$N_J(\bar c)\subseteq N_K(\bar c^-)$
.
(i): Assume
![]() $K\subseteq f^\to (J)$
. If
$K\subseteq f^\to (J)$
. If
![]() $x\in N^*_{K}(\bar c)$
then
$x\in N^*_{K}(\bar c)$
then
![]() $\{n<\omega :\, x\notin c_n\}\in {K}$
, so
$\{n<\omega :\, x\notin c_n\}\in {K}$
, so
i.e.,
![]() $x\in N^*_{J}(\bar c^-)$
; and if
$x\in N^*_{J}(\bar c^-)$
; and if
![]() $x\in N_{J}(\bar c)$
, i.e.,
$x\in N_{J}(\bar c)$
, i.e.,
![]() $\{k<\omega :\, x\in c_k\}\notin {J}$
, then
$\{k<\omega :\, x\in c_k\}\notin {J}$
, then
so
![]() $f^{-1}[\{n<\omega :\, x\in c^{\prime }_n\}]\notin {J}$
, i.e.,
$f^{-1}[\{n<\omega :\, x\in c^{\prime }_n\}]\notin {J}$
, i.e.,
![]() $\{n<\omega :\, x\in c^{\prime }_n\}\notin {K}$
, which means that
$\{n<\omega :\, x\in c^{\prime }_n\}\notin {K}$
, which means that
![]() $x\in N_{K}(\bar c')$
.
$x\in N_{K}(\bar c')$
.
(ii) Assume
![]() $f^\to (K)\subseteq J$
. If
$f^\to (K)\subseteq J$
. If
![]() $x\in N^*_K(\bar c)$
, i.e.,
$x\in N^*_K(\bar c)$
, i.e.,
![]() $\{k<\omega :\, x\notin c_k\}\in K$
, then
$\{k<\omega :\, x\notin c_k\}\in K$
, then
so
![]() $f^{-1}[\{n<\omega :\, x\notin c^{\prime }_n\}]\in K$
, which implies that
$f^{-1}[\{n<\omega :\, x\notin c^{\prime }_n\}]\in K$
, which implies that
![]() $\{n<\omega :\, x\notin c^{\prime }_n\}\in J$
, i.e.,
$\{n<\omega :\, x\notin c^{\prime }_n\}\in J$
, i.e.,
![]() $x\in N^*_J(\bar c')$
; and if
$x\in N^*_J(\bar c')$
; and if
![]() $x\in N_J(\bar c)$
then
$x\in N_J(\bar c)$
then
![]() $\{n<\omega :\, x\in c_n\}\notin J$
, so
$\{n<\omega :\, x\in c_n\}\notin J$
, so
i.e.,
![]() $x\in N_K(\bar c^-)$
.
$x\in N_K(\bar c^-)$
.
Example 2.16. Notice that
![]() $J{\mathrel {\leq _{\mathrm {RB}}}} J\oplus {\mathcal {P}}(\omega )$
, however, J and
$J{\mathrel {\leq _{\mathrm {RB}}}} J\oplus {\mathcal {P}}(\omega )$
, however, J and
![]() ${\mathcal {P}}(\omega )$
should come from different sets. Concretely, if J is an ideal on
${\mathcal {P}}(\omega )$
should come from different sets. Concretely, if J is an ideal on
![]() $\omega $
then
$\omega $
then
![]() $J\oplus {\mathcal {P}}(\omega )$
should be formally taken as
$J\oplus {\mathcal {P}}(\omega )$
should be formally taken as
![]() $J\oplus {\mathcal {P}}({\mathbb {N}}')$
where
$J\oplus {\mathcal {P}}({\mathbb {N}}')$
where
![]() ${\mathbb {N}}'$
is an infinite countable set and
${\mathbb {N}}'$
is an infinite countable set and
![]() $\omega \cap {\mathbb {N}}'=\emptyset $
. Therefore, by Theorem 2.15,
$\omega \cap {\mathbb {N}}'=\emptyset $
. Therefore, by Theorem 2.15,
![]() ${\mathcal {N}}_{J\oplus {\mathcal {P}}(\omega )}={\mathcal {N}}_J$
and
${\mathcal {N}}_{J\oplus {\mathcal {P}}(\omega )}={\mathcal {N}}_J$
and
![]() ${\mathcal {N}}^*_{J\oplus {\mathcal {P}}(\omega )}={\mathcal {N}}^*_J$
(already known at the end of Example 2.13).
${\mathcal {N}}^*_{J\oplus {\mathcal {P}}(\omega )}={\mathcal {N}}^*_J$
(already known at the end of Example 2.13).
Recall the following well-known result that characterizes ideals on
![]() $\omega $
with the Baire property.
$\omega $
with the Baire property.
Theorem 2.17 (Jalani-Naini and Talagrand [Reference Talagrand44]).
Let
![]() ${J}$
be an ideal on
${J}$
be an ideal on
![]() $\omega $
. Then the following statements are equivalent.
$\omega $
. Then the following statements are equivalent.
Therefore, as a consequence of Theorem 2.15, the result below follows.
Theorem 2.18. If
![]() ${J}$
is an ideal on
${J}$
is an ideal on
![]() $\omega $
with the Baire property, then
$\omega $
with the Baire property, then
![]() ${\mathcal {N}}_{J}={\mathcal {N}}$
and
${\mathcal {N}}_{J}={\mathcal {N}}$
and
![]() ${\mathcal {N}}^*_{J}={\mathcal {E}}$
.
${\mathcal {N}}^*_{J}={\mathcal {E}}$
.
So the
![]() $\sigma $
-ideals associated with definable (analytic) ideals do not give new
$\sigma $
-ideals associated with definable (analytic) ideals do not give new
![]() $\sigma $
-ideals on
$\sigma $
-ideals on
![]() ${{}^\omega 2}$
, but they give new characterizations of
${{}^\omega 2}$
, but they give new characterizations of
![]() ${\mathcal {N}}$
and
${\mathcal {N}}$
and
![]() ${\mathcal {E}}$
. The converse of the previous result is also true, which we fully discuss in the next section.
${\mathcal {E}}$
. The converse of the previous result is also true, which we fully discuss in the next section.
3 Ideals without the Baire property
In this section, we study the ideals
![]() ${\mathcal {N}}_J$
and
${\mathcal {N}}_J$
and
![]() ${\mathcal {N}}^*_J$
when J does not have the Baire property. With respect to our main results, we finish to prove Theorem A: an ideal
${\mathcal {N}}^*_J$
when J does not have the Baire property. With respect to our main results, we finish to prove Theorem A: an ideal
![]() ${J}$
on
${J}$
on
![]() $\omega $
without the Baire property gives us new
$\omega $
without the Baire property gives us new
![]() $\sigma $
-ideals
$\sigma $
-ideals
![]() ${\mathcal {N}}_{J}$
and
${\mathcal {N}}_{J}$
and
![]() ${\mathcal {N}}^*_{J}$
. We prove Theorem B as well (see Theorem 3.11).
${\mathcal {N}}^*_{J}$
. We prove Theorem B as well (see Theorem 3.11).
One of the main tools in our study of
![]() ${\mathcal {N}_{J}}$
and
${\mathcal {N}_{J}}$
and
![]() ${\mathcal {N}^*_{J}}$
is the technique of filter games.Footnote
4
For the main results mentioned in the previous paragraph, we will use the meager game.
${\mathcal {N}^*_{J}}$
is the technique of filter games.Footnote
4
For the main results mentioned in the previous paragraph, we will use the meager game.
Definition 3.1. Let
![]() ${F}$
be a filter on
${F}$
be a filter on
![]() $\omega $
. The following game of length
$\omega $
. The following game of length
![]() $\omega $
between two players is called the meager game
$\omega $
between two players is called the meager game
![]() $M_{F}$
:
$M_{F}$
:
-
• In the nth move, Player I plays a finite set
 $A_n\in [\omega ]^{<\omega }$
and Player II responds with a finite set
$A_n\in [\omega ]^{<\omega }$
and Player II responds with a finite set
 $B_n\in [\omega ]^{<\omega }$
disjoint from
$B_n\in [\omega ]^{<\omega }$
disjoint from
 $A_n$
.
$A_n$
. -
• After
 $\omega $
many moves, Player II wins if
$\omega $
many moves, Player II wins if
 $\bigcup {\left \{ {B_n} :\, {n\in \omega } \right \}}\in {F}$
, and Player I wins otherwise.
$\bigcup {\left \{ {B_n} :\, {n\in \omega } \right \}}\in {F}$
, and Player I wins otherwise.
Let us recall an important result from Bartoszyński and Scheepers about the aforementioned game.Footnote 5
Theorem 3.2 [Reference Bartoszyński and Scheepers5].
Let
![]() ${F}$
be a filter on
${F}$
be a filter on
![]() $\omega $
. Then Player I does not have a winning strategy in the meager game for the filter
$\omega $
. Then Player I does not have a winning strategy in the meager game for the filter
![]() ${F}$
if and only if
${F}$
if and only if
![]() ${F}$
is not meager in
${F}$
is not meager in
![]() ${\mathcal {P}}(\omega )$
.
${\mathcal {P}}(\omega )$
.
We use the meager game to show that, whenever J does not have the Baire property, no member of
![]() ${\mathcal {N}}_J$
can be co-meager with respect to any self-supported closed subset of
${\mathcal {N}}_J$
can be co-meager with respect to any self-supported closed subset of
![]() ${{}^\omega 2}$
, i.e., a closed subset of positive measure such that each of its non-empty (relative) open subsets have positive measure.
${{}^\omega 2}$
, i.e., a closed subset of positive measure such that each of its non-empty (relative) open subsets have positive measure.
Main Lemma 3.3. Let
![]() $C\subseteq {}^\omega 2$
be a self-supported closed set. If
$C\subseteq {}^\omega 2$
be a self-supported closed set. If
![]() ${J}$
is not meager then
${J}$
is not meager then
![]() $\displaystyle N_{J}(\bar {c})\cap C$
is not co-meager in C for each
$\displaystyle N_{J}(\bar {c})\cap C$
is not co-meager in C for each
![]() $\bar {c}\in {{\overline {\Omega }}}$
. As a consequence,
$\bar {c}\in {{\overline {\Omega }}}$
. As a consequence,
![]() $Z\cap C$
is not co-meager in C for any
$Z\cap C$
is not co-meager in C for any
![]() $Z\in {\mathcal {N}}_{J}$
.
$Z\in {\mathcal {N}}_{J}$
.
Proof Let
![]() $C\subseteq {}^\omega 2$
be a self-supported closed set, and let
$C\subseteq {}^\omega 2$
be a self-supported closed set, and let
![]() $G\subseteq C$
be a co-meager subset in C. Then there is a sequence
$G\subseteq C$
be a co-meager subset in C. Then there is a sequence
![]() ${\left \langle {D_n} :\, {n\in \omega }\right \rangle }$
of open dense sets in C such that
${\left \langle {D_n} :\, {n\in \omega }\right \rangle }$
of open dense sets in C such that
![]() $\bigcap _{n\in \omega }D_n\subseteq G$
. Moreover, since C is closed, there is a tree T such that
$\bigcap _{n\in \omega }D_n\subseteq G$
. Moreover, since C is closed, there is a tree T such that
![]() $C=[T]$
.
$C=[T]$
.
Consider
![]() $\bar {c}\in {{\overline {\Omega }}}$
and construct the following strategy of Player I for the meager game for
$\bar {c}\in {{\overline {\Omega }}}$
and construct the following strategy of Player I for the meager game for
![]() ${J}^d$
.
${J}^d$
.
The first move:
Player I picks an
![]() $s_0\in T$
such that
$s_0\in T$
such that
![]() $[s_0]\cap C\subseteq D_0$
and chooses
$[s_0]\cap C\subseteq D_0$
and chooses
![]() $n_0<\omega $
such that
$n_0<\omega $
such that
![]() ${\mu \left ({\bigcup _{n\geq n_0}c_n}\right )}<{\mu \left ({C\cap [s_0]}\right )}$
(which exists because
${\mu \left ({\bigcup _{n\geq n_0}c_n}\right )}<{\mu \left ({C\cap [s_0]}\right )}$
(which exists because
![]() $\bar c\in {{\overline {\Omega }}}$
). Player I’s move is
$\bar c\in {{\overline {\Omega }}}$
). Player I’s move is
![]() $n_0$
.
$n_0$
.
Second move and further:
Player II replies with
![]() $B_0\in [\omega ]^{<\omega }$
such that
$B_0\in [\omega ]^{<\omega }$
such that
![]() $n_0\cap B_0=\emptyset $
. Since
$n_0\cap B_0=\emptyset $
. Since
![]() ${\mu \left ({\bigcup _{n\in B_0} c_n}\right )}<{\mu \left ({C\cap [s_0]}\right )}$
,
${\mu \left ({\bigcup _{n\in B_0} c_n}\right )}<{\mu \left ({C\cap [s_0]}\right )}$
,
![]() $C\cap [s_0]\nsubseteq \bigcup _{n\in B_0}c_n$
, so there exists an
$C\cap [s_0]\nsubseteq \bigcup _{n\in B_0}c_n$
, so there exists an
![]() $x_0\in C\cap [s_0]\smallsetminus \bigcup _{n\in B_0} c_n$
. Then Player I finds an
$x_0\in C\cap [s_0]\smallsetminus \bigcup _{n\in B_0} c_n$
. Then Player I finds an
![]() $m_0>|s_0|$
such that
$m_0>|s_0|$
such that
![]() $[x_0{\upharpoonright }m_0]\cap \bigcup _{n\in B_0} c_n=\emptyset $
. Since
$[x_0{\upharpoonright }m_0]\cap \bigcup _{n\in B_0} c_n=\emptyset $
. Since
![]() $D_1$
is dense in C, Player I can pick an
$D_1$
is dense in C, Player I can pick an
![]() $s_1\in T$
such that
$s_1\in T$
such that
![]() $s_0\subseteq x_0{\upharpoonright } m_0\subseteq s_1$
and
$s_0\subseteq x_0{\upharpoonright } m_0\subseteq s_1$
and
![]() $[s_1]\cap C\subseteq D_1$
. Then Player I moves with an
$[s_1]\cap C\subseteq D_1$
. Then Player I moves with an
![]() $n_1\in \omega $
such that
$n_1\in \omega $
such that
![]() ${\mu \left ({\bigcup _{n\geq n_1} c_n}\right )}<{\mu \left ({C\cap [s_1]}\right )}$
. Player II responds with
${\mu \left ({\bigcup _{n\geq n_1} c_n}\right )}<{\mu \left ({C\cap [s_1]}\right )}$
. Player II responds with
![]() $B_1\in [\omega ]^{<\omega }$
such that
$B_1\in [\omega ]^{<\omega }$
such that
![]() $n_1\cap B_1=\emptyset $
, and the game continues in the same way we just described.
$n_1\cap B_1=\emptyset $
, and the game continues in the same way we just described.
Finally, since
![]() ${J}$
is not meager, Player I does not have a winning strategy in the meager game for
${J}$
is not meager, Player I does not have a winning strategy in the meager game for
![]() ${J}^d$
. Hence, there is some match
${J}^d$
. Hence, there is some match
![]() ${\left \langle {(n_k, B_k)} :\, {k\in \omega }\right \rangle }$
where Player I uses the aforementioned strategy and Player II wins. Thus, we have
${\left \langle {(n_k, B_k)} :\, {k\in \omega }\right \rangle }$
where Player I uses the aforementioned strategy and Player II wins. Thus, we have
![]() $F:=\bigcup _{k\in \omega } B_k\in {J}^d$
. Define
$F:=\bigcup _{k\in \omega } B_k\in {J}^d$
. Define
![]() $x:=\bigcup _{k\in \omega }s_k$
. Then,
$x:=\bigcup _{k\in \omega }s_k$
. Then,
![]() $x\in \bigcap _{k\in \omega }D_k$
. On the other hand,
$x\in \bigcap _{k\in \omega }D_k$
. On the other hand,
![]() $x\notin \bigcup _{n\in F}c_n$
(because
$x\notin \bigcup _{n\in F}c_n$
(because
![]() $[s_{k+1}]\cap \bigcup _{n\in B_k}c_k=\emptyset $
) and hence
$[s_{k+1}]\cap \bigcup _{n\in B_k}c_k=\emptyset $
) and hence
![]() $x\notin N_{{J}}(\bar {c})$
.
$x\notin N_{{J}}(\bar {c})$
.
Main Lemma 3.3 shows a connection between
![]() ${\mathcal {N}}_{J}$
and meager sets. First recall the following well-known fact.
${\mathcal {N}}_{J}$
and meager sets. First recall the following well-known fact.
Lemma 3.4 (See, e.g., [Reference Kechris27]).
Let
![]() $A\subseteq {}^\omega 2$
. If A is meager in
$A\subseteq {}^\omega 2$
. If A is meager in
![]() ${{}^\omega 2}$
then, for any
${{}^\omega 2}$
then, for any
![]() $s\in 2^{<\omega }$
,
$s\in 2^{<\omega }$
,
![]() $[s]\cap A$
is not co-meager in
$[s]\cap A$
is not co-meager in
![]() $[s]$
. The converse is true when A has the Baire property.
$[s]$
. The converse is true when A has the Baire property.
Consequences of Main Lemma 3.3 are stated as follows.
Corollary 3.5. If
![]() ${J}$
is an ideal on
${J}$
is an ideal on
![]() $\omega $
, then
$\omega $
, then
![]() ${J}$
does not have the Baire property iff Z is not co-meager in
${J}$
does not have the Baire property iff Z is not co-meager in
![]() ${{}^\omega 2}$
for any
${{}^\omega 2}$
for any
![]() $Z\in {\mathcal {N}}_{J}$
.
$Z\in {\mathcal {N}}_{J}$
.
Proof For the implication from left to right, apply Main Lemma 3.3 to
![]() $C={{}^\omega 2}$
. For the converse, if
$C={{}^\omega 2}$
. For the converse, if
![]() ${J}$
has the Baire property then
${J}$
has the Baire property then
![]() ${\mathcal {N}}_{J}={\mathcal {N}}$
by Theorem 2.18, and it is well-known that
${\mathcal {N}}_{J}={\mathcal {N}}$
by Theorem 2.18, and it is well-known that
![]() ${\mathcal {N}}$
contains a co-meager set in
${\mathcal {N}}$
contains a co-meager set in
![]() ${{}^\omega 2}$
(Rothberger’s Theorem [Reference Rothberger39]).
${{}^\omega 2}$
(Rothberger’s Theorem [Reference Rothberger39]).
Corollary 3.6. Assume that
![]() ${J}$
is an ideal on
${J}$
is an ideal on
![]() $\omega $
without the Baire property. Then, for any
$\omega $
without the Baire property. Then, for any
![]() $Z\in {\mathcal {N}}_{J}$
, Z is meager in
$Z\in {\mathcal {N}}_{J}$
, Z is meager in
![]() ${{}^\omega 2}$
iff it has the Baire property.
${{}^\omega 2}$
iff it has the Baire property.
Proof Assume that
![]() $Z\in {\mathcal {N}}_{J}$
has the Baire property. By Main Lemma 3.3,
$Z\in {\mathcal {N}}_{J}$
has the Baire property. By Main Lemma 3.3,
![]() $Z\cap [s]$
is not co-meager in
$Z\cap [s]$
is not co-meager in
![]() $[s]$
for all
$[s]$
for all
![]() $s\in 2^{<\omega }$
. Therefore, by Lemma 3.4, Z is meager in
$s\in 2^{<\omega }$
. Therefore, by Lemma 3.4, Z is meager in
![]() ${{}^\omega 2}$
.
${{}^\omega 2}$
.
Main Lemma 3.3 gives us the converse of Theorem 2.18 for
![]() ${\mathcal {N}}_{J}$
. Furthermore, we can prove that there is a meager set of Lebesgue measure zero which is not contained in
${\mathcal {N}}_{J}$
. Furthermore, we can prove that there is a meager set of Lebesgue measure zero which is not contained in
![]() ${\mathcal {N}_{J}}$
for non-meager
${\mathcal {N}_{J}}$
for non-meager
![]() ${J}$
.
${J}$
.
Theorem 3.7. Let
![]() ${J}$
be an ideal on
${J}$
be an ideal on
![]() $\omega $
. Then, the following statements are equivalent.
$\omega $
. Then, the following statements are equivalent.
Proof The implication
![]() $\mathrm{(i)}\rightarrow \mathrm{(iii)}$
follows directly from Theorem 2.18. On the other hand, since
$\mathrm{(i)}\rightarrow \mathrm{(iii)}$
follows directly from Theorem 2.18. On the other hand, since
![]() ${\mathcal {M}}\cap {{\mathcal {N}}} \subseteq \mathcal {N}$
the implication
${\mathcal {M}}\cap {{\mathcal {N}}} \subseteq \mathcal {N}$
the implication
![]() $\mathrm{(ii)}\to \mathrm{(i)}$
is obvious.
$\mathrm{(ii)}\to \mathrm{(i)}$
is obvious.
It remains to show
![]() $\mathrm{(iii)}\to \mathrm{(ii)}$
. First, we choose a closed nowhere dense
$\mathrm{(iii)}\to \mathrm{(ii)}$
. First, we choose a closed nowhere dense
![]() $C\subseteq ^\omega 2$
of positive measure, which can be found self-supported (as in the hypothesis of Main Lemma 3.3). Then, we find
$C\subseteq ^\omega 2$
of positive measure, which can be found self-supported (as in the hypothesis of Main Lemma 3.3). Then, we find
![]() $G\subseteq C$
which is co-meager in C and has Lebesgue measure zero. Hence
$G\subseteq C$
which is co-meager in C and has Lebesgue measure zero. Hence
![]() $G\in {\mathcal {M}}\cap {\mathcal {N}}$
, but
$G\in {\mathcal {M}}\cap {\mathcal {N}}$
, but
![]() $G\notin {\mathcal {N}}_{J}$
by Main Lemma 3.3.
$G\notin {\mathcal {N}}_{J}$
by Main Lemma 3.3.
The proof of
![]() $\mathrm{(iii)}\to \mathrm{(ii)}$
is similar to the proof of
$\mathrm{(iii)}\to \mathrm{(ii)}$
is similar to the proof of
![]() ${\mathcal {E}}\subsetneq {\mathcal {M}}\cap {\mathcal {N}}$
from [Reference Bartoszyński and Judah4, Lemma 2.6.1]. Actually, the latter is already implied by
${\mathcal {E}}\subsetneq {\mathcal {M}}\cap {\mathcal {N}}$
from [Reference Bartoszyński and Judah4, Lemma 2.6.1]. Actually, the latter is already implied by
![]() $\mathrm{(ii)}$
(see (2.4)).
$\mathrm{(ii)}$
(see (2.4)).
However,
![]() ${\mathcal {N}}_{J}$
, and even
${\mathcal {N}}_{J}$
, and even
![]() ${\mathcal {N}}^*_{J}$
, contain many non-meager sets when
${\mathcal {N}}^*_{J}$
, contain many non-meager sets when
![]() ${J}$
is not meager. Examples can be obtained from the following construction.
${J}$
is not meager. Examples can be obtained from the following construction.
Definition 3.8. For any non-empty tree
![]() $T\subseteq 2^{<\omega }$
without maximal nodes we define
$T\subseteq 2^{<\omega }$
without maximal nodes we define
![]() $\bar {c}^T$
as follows. Enumerate
$\bar {c}^T$
as follows. Enumerate
![]() $T=\{t_n:n\in \omega \}$
in such a way that
$T=\{t_n:n\in \omega \}$
in such a way that
![]() $t_m\subseteq t_n$
implies
$t_m\subseteq t_n$
implies
![]() $m\leq n$
. By recursion on n, construct
$m\leq n$
. By recursion on n, construct
![]() $\{t^n_k:k\leq n\}\subseteq T$
such that:
$\{t^n_k:k\leq n\}\subseteq T$
such that:
-
(i)
 $t^0_0\in T$
extends
$t^0_0\in T$
extends
 $t_0$
and
$t_0$
and
 $|t^0_0|\geq 1,$
$|t^0_0|\geq 1,$
-
(ii)
 $t^{n+1}_{n+1}\supseteq t_{n+1}$
,
$t^{n+1}_{n+1}\supseteq t_{n+1}$
, -
(iii) for each
 $k\leq n$
,
$k\leq n$
,
 $t^{n+1}_k\supseteq t^n_k$
, and
$t^{n+1}_k\supseteq t^n_k$
, and -
(iv) for each
 $k\leq n+1$
,
$k\leq n+1$
,
 $|t^{n+1}_k|\geq 2n+2$
.
$|t^{n+1}_k|\geq 2n+2$
.
Define
![]() $c^T_n:=\bigcup _{k\leq n}[t^n_k]$
and
$c^T_n:=\bigcup _{k\leq n}[t^n_k]$
and
![]() $\bar {c}^T:={\left \langle {c^T_n} :\, {n\in \omega }\right \rangle }$
. In addition, the inequality
$\bar {c}^T:={\left \langle {c^T_n} :\, {n\in \omega }\right \rangle }$
. In addition, the inequality
![]() ${\mu \left ({c^T_n}\right )}\leq 2^{-n}$
holds, so
${\mu \left ({c^T_n}\right )}\leq 2^{-n}$
holds, so
![]() $\bar c^T\in {{\overline {\Omega }}}$
.
$\bar c^T\in {{\overline {\Omega }}}$
.
In general, for any sequence
![]() $\bar \varepsilon ={\left \langle {\varepsilon _n} :\, {n<\omega }\right \rangle }$
of positive reals, it is possible to construct a similar
$\bar \varepsilon ={\left \langle {\varepsilon _n} :\, {n<\omega }\right \rangle }$
of positive reals, it is possible to construct a similar
![]() $\bar {c}^{T,\bar \varepsilon }$
such that
$\bar {c}^{T,\bar \varepsilon }$
such that
![]() ${\mu \left ({c^{T,\bar \varepsilon }_n}\right )}<\varepsilon _n$
for all
${\mu \left ({c^{T,\bar \varepsilon }_n}\right )}<\varepsilon _n$
for all
![]() $n<\omega $
, that is,
$n<\omega $
, that is,
![]() $\bar {c}^{T,\bar \varepsilon }\in \Omega ^*_{\bar \varepsilon }$
. For this, we just need to modify the length of each
$\bar {c}^{T,\bar \varepsilon }\in \Omega ^*_{\bar \varepsilon }$
. For this, we just need to modify the length of each
![]() $t^n_k$
accordingly.
$t^n_k$
accordingly.
Main Lemma 3.9. Let
![]() $T\subseteq 2^{<\omega }$
be a non-empty tree without maximal nodes and let
$T\subseteq 2^{<\omega }$
be a non-empty tree without maximal nodes and let
![]() ${J}$
be a non-meager ideal on
${J}$
be a non-meager ideal on
![]() $\omega $
. Then
$\omega $
. Then
![]() $N^*_{J}(\bar {c}^T)\cap G\neq \emptyset $
for every co-meager set
$N^*_{J}(\bar {c}^T)\cap G\neq \emptyset $
for every co-meager set
![]() $G\subseteq [T]$
in
$G\subseteq [T]$
in
![]() $[T]$
, i.e.,
$[T]$
, i.e.,
![]() $N^*_{J}(\bar {c}^T)$
is not meager in
$N^*_{J}(\bar {c}^T)$
is not meager in
![]() $[T]$
.
$[T]$
.
In other words, for any non-empty closed
![]() $H\subseteq {{}^\omega 2}$
there is some
$H\subseteq {{}^\omega 2}$
there is some
![]() $\bar {c}^H\in {{\overline {\Omega }}}$
such that, for any non-meager ideal
$\bar {c}^H\in {{\overline {\Omega }}}$
such that, for any non-meager ideal
![]() ${J}$
on
${J}$
on
![]() $\omega $
,
$\omega $
,
![]() $N^*_{J}(\bar c^H)\cap H$
is non-meager in H.
$N^*_{J}(\bar c^H)\cap H$
is non-meager in H.
Proof Let
![]() $G\subseteq [T]$
be co-meager in
$G\subseteq [T]$
be co-meager in
![]() $[T]$
. Then, there is a sequence
$[T]$
. Then, there is a sequence
![]() ${\left \langle {D_n} :\, {n\in \omega }\right \rangle }$
of open dense sets in
${\left \langle {D_n} :\, {n\in \omega }\right \rangle }$
of open dense sets in
![]() $[T]$
such that
$[T]$
such that
![]() $\bigcap _{n\in \omega }D_n\subseteq G$
. We look for an
$\bigcap _{n\in \omega }D_n\subseteq G$
. We look for an
![]() $x\in N^*_{J}(\bar {c}^T)\cap \bigcap _{n\in \omega }D_n$
by using the non-meager game.
$x\in N^*_{J}(\bar {c}^T)\cap \bigcap _{n\in \omega }D_n$
by using the non-meager game.
Construct the following strategy of Player I for the non-meager game for
![]() ${J}^d$
along with fragments of the desired x.
${J}^d$
along with fragments of the desired x.
The first move:
Player I chooses some
![]() $s_0\in T$
extending
$s_0\in T$
extending
![]() $t^0_0$
such that
$t^0_0$
such that
![]() $[s_0]\cap [T]\subseteq D_0$
. Since
$[s_0]\cap [T]\subseteq D_0$
. Since
![]() $s_0\in T$
,
$s_0\in T$
,
![]() $s_0=t_{n_0}$
for some
$s_0=t_{n_0}$
for some
![]() $n_0\in \omega $
. Player I moves with
$n_0\in \omega $
. Player I moves with
![]() $A_0:=n_0+1$
.
$A_0:=n_0+1$
.
Second move and further:
Player II replies with
![]() $B_0$
. Since
$B_0$
. Since
![]() $B_0\cap A_0=\emptyset $
, by (ii)–(iii) of Definition 3.8, Player I can extend
$B_0\cap A_0=\emptyset $
, by (ii)–(iii) of Definition 3.8, Player I can extend
![]() $s_0$
to some
$s_0$
to some
![]() $s^{\prime }_0\in T$
such that, for any
$s^{\prime }_0\in T$
such that, for any
![]() $\ell \in B_0$
,
$\ell \in B_0$
,
![]() $s^{\prime }_0$
extends
$s^{\prime }_0$
extends
![]() $t^\ell _{n_0}$
, and further finds
$t^\ell _{n_0}$
, and further finds
![]() $s_1\in T$
extending
$s_1\in T$
extending
![]() $s^{\prime }_0$
such that
$s^{\prime }_0$
such that
![]() $[s_1]\cap [T]\subseteq D_1$
. Here,
$[s_1]\cap [T]\subseteq D_1$
. Here,
![]() $s_1=t_{n_1}$
for some
$s_1=t_{n_1}$
for some
![]() $n_1\in \omega $
, and Player I moves with
$n_1\in \omega $
, and Player I moves with
![]() $A_1:=n_1+1$
. Player II would reply with some
$A_1:=n_1+1$
. Player II would reply with some
![]() $B_1$
not intersecting
$B_1$
not intersecting
![]() $A_1$
, and Player I continues playing in the same way.
$A_1$
, and Player I continues playing in the same way.
Now, since
![]() ${J}$
is not meager, Player I does not have a winning strategy. In particular, there is some match
${J}$
is not meager, Player I does not have a winning strategy. In particular, there is some match
![]() ${\left \langle {(A_n,B_n)} :\, {n\in \omega }\right \rangle }$
of the game where Player I uses the strategy defined above and Player II wins, i.e.,
${\left \langle {(A_n,B_n)} :\, {n\in \omega }\right \rangle }$
of the game where Player I uses the strategy defined above and Player II wins, i.e.,
![]() $F:=\bigcup _{n\in \omega }B_n$
is in
$F:=\bigcup _{n\in \omega }B_n$
is in
![]() ${J}^d$
. On the other hand, Player I constructed the increasing sequence
${J}^d$
. On the other hand, Player I constructed the increasing sequence
![]() ${\left \langle {s_n} :\, {n\in \omega }\right \rangle }$
of members of T, so
${\left \langle {s_n} :\, {n\in \omega }\right \rangle }$
of members of T, so
![]() $x:=\bigcup _{n\in \omega }s_n$
is a branch of the tree. By the definition of the strategy, we have that
$x:=\bigcup _{n\in \omega }s_n$
is a branch of the tree. By the definition of the strategy, we have that
![]() $x\in c^T_m$
for any
$x\in c^T_m$
for any
![]() $m\in F$
, so
$m\in F$
, so
![]() $x\in N^*_{J}(\bar {c}^T)$
. Also
$x\in N^*_{J}(\bar {c}^T)$
. Also
![]() $x\in D_n$
for every
$x\in D_n$
for every
![]() $n\in \omega $
.
$n\in \omega $
.
As a consequence for
![]() $T=2^{<\omega }$
, we conclude that
$T=2^{<\omega }$
, we conclude that
![]() ${\mathcal {N}^*_{J}}$
contains non-meager subsets of
${\mathcal {N}^*_{J}}$
contains non-meager subsets of
![]() ${{}^\omega 2}$
when
${{}^\omega 2}$
when
![]() ${J}$
is an ideal on
${J}$
is an ideal on
![]() $\omega $
without the Baire property. Moreover, let us emphasize that the same is true for
$\omega $
without the Baire property. Moreover, let us emphasize that the same is true for
![]() ${\mathcal {N}_{J}}$
as well (because
${\mathcal {N}_{J}}$
as well (because
![]() $N^*_{J}(\bar c)\subseteq N_{J}(\bar c)$
).
$N^*_{J}(\bar c)\subseteq N_{J}(\bar c)$
).
Corollary 3.10. If
![]() ${J}$
is not meager then
${J}$
is not meager then
![]() $N^*_{J}(\bar {c}^T)$
and
$N^*_{J}(\bar {c}^T)$
and
![]() $N_{J}(\bar {c}^T)$
are not meager in
$N_{J}(\bar {c}^T)$
are not meager in
![]() $^\omega 2$
.
$^\omega 2$
.
In contrast with Main Lemma 3.9, if
![]() ${J}$
has the Baire property then
${J}$
has the Baire property then
![]() $N^*_{J}(\bar c^T)$
is meager in
$N^*_{J}(\bar c^T)$
is meager in
![]() ${{}^\omega 2}$
(and even
${{}^\omega 2}$
(and even
![]() $N^*_{J}(\bar c^T)\cap [T]$
is meager in
$N^*_{J}(\bar c^T)\cap [T]$
is meager in
![]() $[T]$
when
$[T]$
when
![]() ${\mu \left ({[T]}\right )}>0$
) because
${\mu \left ({[T]}\right )}>0$
) because
![]() $N_{J}^*(\bar c^T)\in {\mathcal {E}}$
by Theorem 2.18.
$N_{J}^*(\bar c^T)\in {\mathcal {E}}$
by Theorem 2.18.
As a consequence of Main Lemma 3.9, we can finally conclude that
![]() ${\mathcal {N}}^*_{J}={\mathcal {E}}$
iff
${\mathcal {N}}^*_{J}={\mathcal {E}}$
iff
![]() ${J}$
has the Baire property.
${J}$
has the Baire property.
Theorem 3.11. Let
![]() ${J}$
be an ideal on
${J}$
be an ideal on
![]() $\omega $
. Then the following statements are equivalent:
$\omega $
. Then the following statements are equivalent:
Proof
![]() $\mathrm{(iv)}\rightarrow \mathrm{(i)}$
follows by Corollary 3.10;
$\mathrm{(iv)}\rightarrow \mathrm{(i)}$
follows by Corollary 3.10;
![]() $\mathrm{(i)}\rightarrow \mathrm{(ii)}$
is obvious;
$\mathrm{(i)}\rightarrow \mathrm{(ii)}$
is obvious;
![]() $\mathrm{(ii)}\rightarrow \mathrm{(iii)}$
is a consequence of
$\mathrm{(ii)}\rightarrow \mathrm{(iii)}$
is a consequence of
![]() ${\mathcal {E}}\subseteq {\mathcal {M}}\cap {\mathcal {N}}$
;
${\mathcal {E}}\subseteq {\mathcal {M}}\cap {\mathcal {N}}$
;
![]() $\mathrm{(iii)}\rightarrow \mathrm{(iv)}$
is a consequence of Theorem 2.18.
$\mathrm{(iii)}\rightarrow \mathrm{(iv)}$
is a consequence of Theorem 2.18.
In the case of
![]() ${\mathcal {N}}_{J}$
, whether
${\mathcal {N}}_{J}$
, whether
![]() ${J}$
is meager or not,
${J}$
is meager or not,
![]() ${\mathcal {N}}_{J}$
contains non-meager sets.
${\mathcal {N}}_{J}$
contains non-meager sets.
Corollary 3.12. For every ideal
![]() ${J}$
on
${J}$
on
![]() $\omega $
,
$\omega $
,
![]() ${\mathcal {N}}_{J}\nsubseteq {\mathcal {M}}$
and
${\mathcal {N}}_{J}\nsubseteq {\mathcal {M}}$
and
![]() ${\mathcal {N}_{J}}\nsubseteq {\mathcal {M}}\cap {{\mathcal {N}}}$
.
${\mathcal {N}_{J}}\nsubseteq {\mathcal {M}}\cap {{\mathcal {N}}}$
.
Proof Since
![]() ${\mathcal {N}}_{J}^*\subseteq {\mathcal {N}}_{J}$
, the conclusion is clear by Theorem 3.11 when
${\mathcal {N}}_{J}^*\subseteq {\mathcal {N}}_{J}$
, the conclusion is clear by Theorem 3.11 when
![]() ${J}$
is not meager. Otherwise
${J}$
is not meager. Otherwise
![]() ${\mathcal {N}}_{J}={\mathcal {N}}$
, and
${\mathcal {N}}_{J}={\mathcal {N}}$
, and
![]() ${\mathcal {N}}$
contains a co-meager set.
${\mathcal {N}}$
contains a co-meager set.
Figure 2 summarizes the situation in Theorems 3.7 and 3.11 when
![]() ${J}$
is a non-meager ideal on
${J}$
is a non-meager ideal on
![]() $\omega $
.
$\omega $
.

Figure 2 The situation when
![]() ${J}$
is an ideal on
${J}$
is an ideal on
![]() $\omega $
without the Baire property. An arrow denotes
$\omega $
without the Baire property. An arrow denotes
![]() $\subseteq $
, while a crossed arrow denotes
$\subseteq $
, while a crossed arrow denotes
![]() $\nsubseteq $
. The arrow on the bottom could be reversed, e.g., when
$\nsubseteq $
. The arrow on the bottom could be reversed, e.g., when
![]() ${J}$
is a maximal ideal.
${J}$
is a maximal ideal.
4 The effect of nearly coherence of filters
In this section, we prove a characterization of nearly coherence of filters (or ideals) in terms of the ideals
![]() ${\mathcal {N}}_{J}$
and
${\mathcal {N}}_{J}$
and
![]() ${\mathcal {N}}^*_{J}$
. We first recall the notion of nearly coherence.
${\mathcal {N}}^*_{J}$
. We first recall the notion of nearly coherence.
Definition 4.1 (A. Blass [Reference Blass7]).
Two filters
![]() ${F}_0$
and
${F}_0$
and
![]() ${F}_1$
on
${F}_1$
on
![]() $\omega $
are nearly coherent if there is a finite-to-one function
$\omega $
are nearly coherent if there is a finite-to-one function
![]() $\varphi \in {}^\omega \omega $
such that
$\varphi \in {}^\omega \omega $
such that
![]() $\varphi ^\to ({F}_0)\cup \varphi ^\to ({F}_1)$
has the finite intersection property. Dually, we say that two ideals
$\varphi ^\to ({F}_0)\cup \varphi ^\to ({F}_1)$
has the finite intersection property. Dually, we say that two ideals
![]() ${J}_0$
and
${J}_0$
and
![]() ${J}_1$
are nearly coherent if there is a finite-to-one function
${J}_1$
are nearly coherent if there is a finite-to-one function
![]() $\varphi \in {}^\omega \omega $
such that
$\varphi \in {}^\omega \omega $
such that
![]() $\varphi ^\to ({J}_0)\cup \varphi ^\to ({J}_1)$
is contained in some ideal.
$\varphi ^\to ({J}_0)\cup \varphi ^\to ({J}_1)$
is contained in some ideal.
If
![]() $J_0$
and
$J_0$
and
![]() $J_1$
are nearly coherent ideals on
$J_1$
are nearly coherent ideals on
![]() $\omega $
, then there is some ideal K in
$\omega $
, then there is some ideal K in
![]() $\omega $
which is
$\omega $
which is
![]() ${\mathrel {\leq _{\overline {\mathrm {KB}}}}}$
-above both
${\mathrel {\leq _{\overline {\mathrm {KB}}}}}$
-above both
![]() $J_0$
and
$J_0$
and
![]() $J_1$
. As a consequence of Theorem 2.15(b), the following result follows.
$J_1$
. As a consequence of Theorem 2.15(b), the following result follows.
Lemma 4.2. If
![]() ${J}_0$
and
${J}_0$
and
![]() ${J}_1$
are nearly coherent ideals on
${J}_1$
are nearly coherent ideals on
![]() $\omega $
, then there is some ideal
$\omega $
, then there is some ideal
![]() ${K}$
on
${K}$
on
![]() $\omega $
such that
$\omega $
such that
![]() ${\mathcal {N}}^*_{{J}_0}\cup {\mathcal {N}}^*_{{J}_1} \subseteq {\mathcal {N}}^*_{K}\subseteq {\mathcal {N}}_{K} \subseteq {\mathcal {N}}_{{J}_0}\cap {\mathcal {N}}_{{J}_1}$
(see Figure 3).
${\mathcal {N}}^*_{{J}_0}\cup {\mathcal {N}}^*_{{J}_1} \subseteq {\mathcal {N}}^*_{K}\subseteq {\mathcal {N}}_{K} \subseteq {\mathcal {N}}_{{J}_0}\cap {\mathcal {N}}_{{J}_1}$
(see Figure 3).

Figure 3 Situation describing Lemma 4.2 (an arrow denotes
![]() $\subseteq $
).
$\subseteq $
).
Since
![]() ${\mathcal {N}}^*_{J}={\mathcal {N}}_{J}$
for any maximal ideal
${\mathcal {N}}^*_{J}={\mathcal {N}}_{J}$
for any maximal ideal
![]() ${J}$
on
${J}$
on
![]() $\omega $
, we immediately obtain the following consequence.
$\omega $
, we immediately obtain the following consequence.
Corollary 4.3. If
![]() ${J}$
and
${J}$
and
![]() ${K}$
are nearly coherent ideals and
${K}$
are nearly coherent ideals and
![]() ${K}$
is maximal, then
${K}$
is maximal, then
![]() ${\mathcal {N}}^*_{J}\subseteq {\mathcal {N}}_{K}\subseteq {\mathcal {N}}_{J}$
. In particular, if
${\mathcal {N}}^*_{J}\subseteq {\mathcal {N}}_{K}\subseteq {\mathcal {N}}_{J}$
. In particular, if
![]() ${J}$
is also a maximal ideal, then
${J}$
is also a maximal ideal, then
![]() ${\mathcal {N}}_{J}={\mathcal {N}}_{K}$
.
${\mathcal {N}}_{J}={\mathcal {N}}_{K}$
.
A. Blass [Reference Blass7] has introduced the following principle, which was proved consistent with ZFC by Blass and Shelah [Reference Blass and Shelah11].
-
(NCF) Near coherence of filters: Any pair of filters on
 $\omega $
are nearly coherent.
$\omega $
are nearly coherent.
In fact,
![]() $\mathfrak {u}<\mathfrak {g}$
(which holds in Miller model [Reference Blass8, Reference Blass and Shelah12]) implies NCF [Reference Blass9, Corollary 9.18]. On the other hand, it is possible to obtain not nearly coherence pairs of filters under CH and in random model [Reference Blass7, Section 4], as well as in Cohen model (e.g., Theorem 6.3).
$\mathfrak {u}<\mathfrak {g}$
(which holds in Miller model [Reference Blass8, Reference Blass and Shelah12]) implies NCF [Reference Blass9, Corollary 9.18]. On the other hand, it is possible to obtain not nearly coherence pairs of filters under CH and in random model [Reference Blass7, Section 4], as well as in Cohen model (e.g., Theorem 6.3).
The following is a consequence of Corollary 4.3.
Corollary 4.4.
NCF implies that all
![]() ${\mathcal {N}}_{J}$
with
${\mathcal {N}}_{J}$
with
![]() ${J}$
maximal ideal on
${J}$
maximal ideal on
![]() $\omega $
are the same.
$\omega $
are the same.
We prove the converse of Lemma 4.2 and of Corollaries 4.3 and 4.4, which gives us a characterization of nearly coherence and NCF. For this purpose, we use the following game, formulated by T. Eisworth, that characterizes nearly coherence.
Definition 4.5 (Eisworth [Reference Eisworth20]).
Let
![]() ${F}_0$
,
${F}_0$
,
![]() ${F}_1$
be two filters on
${F}_1$
be two filters on
![]() $\omega $
. The following game of length
$\omega $
. The following game of length
![]() $\omega $
between two players is called the nearly coherence game
$\omega $
between two players is called the nearly coherence game
![]() $C_{{F}_0,{F}_1}$
:
$C_{{F}_0,{F}_1}$
:
-
• In the nth move, Player I plays a finite set
 $A_n\in [\omega ]^{<\omega }$
and Player II responds with a finite set
$A_n\in [\omega ]^{<\omega }$
and Player II responds with a finite set
 $B_n\in [\omega ]^{<\omega }$
disjoint from
$B_n\in [\omega ]^{<\omega }$
disjoint from
 $A_n$
.
$A_n$
. -
• After
 $\omega $
many moves, Player II wins if
$\omega $
many moves, Player II wins if
 $\bigcup {\left \{ {B_{2n+i}} :\, {n\in \omega } \right \}}\in {F}_i$
for
$\bigcup {\left \{ {B_{2n+i}} :\, {n\in \omega } \right \}}\in {F}_i$
for
 $i\in \{0,1\}$
. Otherwise, Player I wins.
$i\in \{0,1\}$
. Otherwise, Player I wins.
Theorem 4.6 (Eisworth [Reference Eisworth20]).
Let
![]() ${F}_0$
,
${F}_0$
,
![]() ${F}_1$
be two filters on
${F}_1$
be two filters on
![]() $\omega $
. Then
$\omega $
. Then
![]() ${F}_0$
and
${F}_0$
and
![]() ${F}_1$
are nearly coherent iff Player I has a winning strategy of the game
${F}_1$
are nearly coherent iff Player I has a winning strategy of the game
![]() $C_{{F}_0,{F}_1}$
.
$C_{{F}_0,{F}_1}$
.
We use the nearly coherence game
![]() $C_{{F}_0,{F}_1}$
to prove the following technical lemma.
$C_{{F}_0,{F}_1}$
to prove the following technical lemma.
Main Lemma 4.7. Let
![]() $C\subseteq {}^\omega 2$
be a closed self-supported set. If
$C\subseteq {}^\omega 2$
be a closed self-supported set. If
![]() ${J}$
and
${J}$
and
![]() ${K}$
are not nearly coherent ideals on
${K}$
are not nearly coherent ideals on
![]() $\omega $
then
$\omega $
then
![]() $N^*_{J}(\bar {c}^T)\notin {\mathcal {N}}_{K}$
where T is the tree without maximal nodes such that
$N^*_{J}(\bar {c}^T)\notin {\mathcal {N}}_{K}$
where T is the tree without maximal nodes such that
![]() $C=[T]$
, and
$C=[T]$
, and
![]() $\bar c^T$
is as in Definition 3.8.
$\bar c^T$
is as in Definition 3.8.
Proof We use the nearly coherence game
![]() $C_{{J}^d,{K}^d}$
and build a strategy for Player I, in order to get an
$C_{{J}^d,{K}^d}$
and build a strategy for Player I, in order to get an
![]() $x\in N^*_{J}(\bar {c}^T)\smallsetminus N_{K}(\bar {c}')$
for any
$x\in N^*_{J}(\bar {c}^T)\smallsetminus N_{K}(\bar {c}')$
for any
![]() $\bar {c}'\in {{\overline {\Omega }}}$
.
$\bar {c}'\in {{\overline {\Omega }}}$
.
The first move: Player I first moves with
![]() $A_0=\{0\}$
, and put
$A_0=\{0\}$
, and put
![]() $s_0:= t_0$
(which is the empty sequence).
$s_0:= t_0$
(which is the empty sequence).
The second and third moves, and further:
After Player II replies with
![]() $B_0\subseteq \omega \smallsetminus A_0$
, Player I finds
$B_0\subseteq \omega \smallsetminus A_0$
, Player I finds
![]() $s_1\supseteq s_0$
in T such that
$s_1\supseteq s_0$
in T such that
![]() $s_1\supseteq t^n_0$
for every
$s_1\supseteq t^n_0$
for every
![]() $n\in B_0$
, and further finds
$n\in B_0$
, and further finds
![]() $n_1\geq |s_1|$
such that
$n_1\geq |s_1|$
such that
![]() $\mu \left (\bigcup _{\ell \geq n_1}c^{\prime }_\ell \right )<\mu (C\cap [s_1])$
, which implies that there is some
$\mu \left (\bigcup _{\ell \geq n_1}c^{\prime }_\ell \right )<\mu (C\cap [s_1])$
, which implies that there is some
![]() $x_1\in C\cap [s_1]\smallsetminus \bigcup _{\ell \geq n_1}c^{\prime }_\ell $
. Player I moves with
$x_1\in C\cap [s_1]\smallsetminus \bigcup _{\ell \geq n_1}c^{\prime }_\ell $
. Player I moves with
![]() $A_1=n_1+1$
.
$A_1=n_1+1$
.
After Player II replies with
![]() $B_1\subseteq \omega \smallsetminus A_1$
, Player I finds some
$B_1\subseteq \omega \smallsetminus A_1$
, Player I finds some
![]() $m_2\geq n_1$
such that
$m_2\geq n_1$
such that
![]() $[s_2]\cap \bigcup _{n\in B_1}c^{\prime }_n=\emptyset $
where
$[s_2]\cap \bigcup _{n\in B_1}c^{\prime }_n=\emptyset $
where
![]() $s_2:=x_1{\upharpoonright }m_2$
. Player I moves
$s_2:=x_1{\upharpoonright }m_2$
. Player I moves
![]() $A_2=n_2+1$
where
$A_2=n_2+1$
where
![]() $n_2<\omega $
is such that
$n_2<\omega $
is such that
![]() $s_2=t_{n_2}$
.
$s_2=t_{n_2}$
.
Afterwards, Player II moves with
![]() $B_2\subseteq \omega \smallsetminus A_2$
, and the same dynamic is repeated: Player I finds an
$B_2\subseteq \omega \smallsetminus A_2$
, and the same dynamic is repeated: Player I finds an
![]() $s_3\supseteq s_2$
in T such that
$s_3\supseteq s_2$
in T such that
![]() $s_3\supseteq t^n_{n_2}$
for every
$s_3\supseteq t^n_{n_2}$
for every
![]() $n\in B_2$
, and some
$n\in B_2$
, and some
![]() $n_3\geq |s_3|$
such that
$n_3\geq |s_3|$
such that
![]() $\mu \left ( \bigcup _{\ell \geq n_3} c^{\prime }_\ell \right )<\mu (C\cap [s_3])$
, which implies that there is an
$\mu \left ( \bigcup _{\ell \geq n_3} c^{\prime }_\ell \right )<\mu (C\cap [s_3])$
, which implies that there is an
![]() $x_3\in C\cap [s_3]\smallsetminus \bigcup _{\ell \geq n_3}c^{\prime }_\ell $
. Player I moves with
$x_3\in C\cap [s_3]\smallsetminus \bigcup _{\ell \geq n_3}c^{\prime }_\ell $
. Player I moves with
![]() $A_3=n_3+1$
, and the game continues as described so far.
$A_3=n_3+1$
, and the game continues as described so far.
Since Player I does not have a winning strategy, there is some run as described above where Player II wins. Thus,
![]() $F_0:=\bigcup _{n\in \omega }B_{2n}\in {J}^d$
and
$F_0:=\bigcup _{n\in \omega }B_{2n}\in {J}^d$
and
![]() $F_1:=\bigcup _{n\in \omega }B_{2n+1}\in {K}^d$
. Set
$F_1:=\bigcup _{n\in \omega }B_{2n+1}\in {K}^d$
. Set
![]() $x:=\bigcup _{n\in \omega }s_n$
. Note that
$x:=\bigcup _{n\in \omega }s_n$
. Note that
![]() $x\in c^T_\ell $
for any
$x\in c^T_\ell $
for any
![]() $\ell \in F_0$
, and
$\ell \in F_0$
, and
![]() $x\notin c^{\prime }_\ell $
for any
$x\notin c^{\prime }_\ell $
for any
![]() $\ell \in F_1$
, which means that
$\ell \in F_1$
, which means that
![]() $x\in N^*_{J}(\bar {c}^T)$
and
$x\in N^*_{J}(\bar {c}^T)$
and
![]() $x\notin N_{K}(\bar {c}')$
.
$x\notin N_{K}(\bar {c}')$
.
An application of the previous result to
![]() $C={{}^\omega 2}$
yields the following distinction.
$C={{}^\omega 2}$
yields the following distinction.
Theorem 4.8. If
![]() ${J}$
and
${J}$
and
![]() ${K}$
are not near-coherent ideals on
${K}$
are not near-coherent ideals on
![]() $\omega $
then
$\omega $
then
![]() ${\mathcal {N}}^*_{J}\nsubseteq {\mathcal {N}}_{K}$
and
${\mathcal {N}}^*_{J}\nsubseteq {\mathcal {N}}_{K}$
and
![]() ${\mathcal {N}}^*_{K}\nsubseteq {\mathcal {N}}_{J}$
. In particular,
${\mathcal {N}}^*_{K}\nsubseteq {\mathcal {N}}_{J}$
. In particular,
![]() ${\mathcal {N}_{{K}}}\neq {\mathcal {N}_{J}}$
and
${\mathcal {N}_{{K}}}\neq {\mathcal {N}_{J}}$
and
![]() ${\mathcal {N}}^*_{J}\neq {\mathcal {N}}^*_{K}$
.
${\mathcal {N}}^*_{J}\neq {\mathcal {N}}^*_{K}$
.
It is clear that
![]() ${\mathrm {Fin}}$
is nearly coherent with any filter on
${\mathrm {Fin}}$
is nearly coherent with any filter on
![]() $\omega $
. Therefore, any pair of not nearly coherent filters must be non-meager. The following is a consequence of Theorems 3.7 and 3.11.
$\omega $
. Therefore, any pair of not nearly coherent filters must be non-meager. The following is a consequence of Theorems 3.7 and 3.11.
Corollary 4.9. Let
![]() ${J}$
and
${J}$
and
![]() ${K}$
be not nearly coherent ideals on
${K}$
be not nearly coherent ideals on
![]() $\omega $
. Then the ideals
$\omega $
. Then the ideals
![]() $\mathcal {E}$
,
$\mathcal {E}$
,
![]() ${\mathcal {N}^*_{J}}$
,
${\mathcal {N}^*_{J}}$
,
![]() ${\mathcal {N}_{{K}}}$
and
${\mathcal {N}_{{K}}}$
and
![]() $\mathcal {N}$
are pairwise different.
$\mathcal {N}$
are pairwise different.
The situation in Theorem 4.8 and Corollary 4.9 is illustrated in Figure 4.

Figure 4 Diagram corresponding to the situation in Theorem 4.8 where
![]() ${J}$
and
${J}$
and
![]() ${K}$
are not nearly coherent ideals on
${K}$
are not nearly coherent ideals on
![]() $\omega $
. An arrow denotes
$\omega $
. An arrow denotes
![]() $\subseteq $
, and a crossed arrow denotes
$\subseteq $
, and a crossed arrow denotes
![]() $\nsubseteq $
. The arrow on the top could be reversed, e.g., when
$\nsubseteq $
. The arrow on the top could be reversed, e.g., when
![]() ${K}$
is a maximal ideal (likewise for the arrow on the bottom).
${K}$
is a maximal ideal (likewise for the arrow on the bottom).
We summarize our results as a characterization of nearly coherence.
Theorem 4.10. Let J and K be ideals on
![]() $\omega $
. The following statements are equivalent.
$\omega $
. The following statements are equivalent.
-
(i) J and K are nearly coherent.
-
(ii) There is some ideal
 $K'$
on
$K'$
on
 $\omega $
such that
$\omega $
such that
 $J {\mathrel {\leq _{\overline {\mathrm {KB}}}}} K'$
and
$J {\mathrel {\leq _{\overline {\mathrm {KB}}}}} K'$
and
 $K{\mathrel {\leq _{\overline {\mathrm {KB}}}}} K'$
.
$K{\mathrel {\leq _{\overline {\mathrm {KB}}}}} K'$
. -
(iii) There is some ideal
 $K'$
on
$K'$
on
 $\omega $
such that
$\omega $
such that
 ${\mathcal {N}}^*_J\cup {\mathcal {N}}^*_{K}\subseteq {\mathcal {N}}^*_{K'}\subseteq {\mathcal {N}}_{K'}\subseteq {\mathcal {N}}_J \cap {\mathcal {N}}_K$
.
${\mathcal {N}}^*_J\cup {\mathcal {N}}^*_{K}\subseteq {\mathcal {N}}^*_{K'}\subseteq {\mathcal {N}}_{K'}\subseteq {\mathcal {N}}_J \cap {\mathcal {N}}_K$
. -
(iv)
 ${\mathcal {N}}^*_J\subseteq {\mathcal {N}}_K$
.
${\mathcal {N}}^*_J\subseteq {\mathcal {N}}_K$
.
Proof
![]() $\mathrm{(i)}\mathrel {\Rightarrow } \mathrm{(ii)}$
is obvious;
$\mathrm{(i)}\mathrel {\Rightarrow } \mathrm{(ii)}$
is obvious;
![]() $\mathrm{(ii)}\mathrel {\Rightarrow } \mathrm{(iii)}$
is immediate from Theorem 2.15;
$\mathrm{(ii)}\mathrel {\Rightarrow } \mathrm{(iii)}$
is immediate from Theorem 2.15;
![]() $\mathrm{(iii)}\mathrel {\Rightarrow }\mathrm{(iv)}$
is obvious; and
$\mathrm{(iii)}\mathrel {\Rightarrow }\mathrm{(iv)}$
is obvious; and
![]() $\mathrm{(iv)}\mathrel {\Rightarrow } \mathrm{(i)}$
follows by (the contrapositive of) Theorem 4.8.
$\mathrm{(iv)}\mathrel {\Rightarrow } \mathrm{(i)}$
follows by (the contrapositive of) Theorem 4.8.
The non-nearly coherence of filters also gives us examples of non-meager ideals J such that
![]() ${\mathcal {N}}^*_J\neq {\mathcal {N}}_J$
. We do not know how to construct such an example in ZFC.
${\mathcal {N}}^*_J\neq {\mathcal {N}}_J$
. We do not know how to construct such an example in ZFC.
Lemma 4.11. Assume that
![]() $J_1$
and
$J_1$
and
![]() $J_2$
are non-nearly coherent ideals on
$J_2$
are non-nearly coherent ideals on
![]() $\omega $
. Then
$\omega $
. Then
![]() $J_1\oplus J_2$
is non-meager and
$J_1\oplus J_2$
is non-meager and
![]() ${\mathcal {N}}^*_{J_1\oplus J_2}\neq {\mathcal {N}}_{J_1\oplus J_2}$
.
${\mathcal {N}}^*_{J_1\oplus J_2}\neq {\mathcal {N}}_{J_1\oplus J_2}$
.
Proof Partition
![]() $\omega ={\mathbb {N}}_1\cup {\mathbb {N}}_2$
into two infinite sets, let
$\omega ={\mathbb {N}}_1\cup {\mathbb {N}}_2$
into two infinite sets, let
![]() $g_e\colon \omega \to {\mathbb {N}}_e$
be a bijection for each
$g_e\colon \omega \to {\mathbb {N}}_e$
be a bijection for each
![]() $e\in \{1,2\}$
, and let
$e\in \{1,2\}$
, and let
![]() $J^{\prime }_e= g_e^\to (J_e)$
, which is an ideal on
$J^{\prime }_e= g_e^\to (J_e)$
, which is an ideal on
![]() ${\mathbb {N}}_e$
isomorphic with
${\mathbb {N}}_e$
isomorphic with
![]() $J_e$
. Here, our interpretation of
$J_e$
. Here, our interpretation of
![]() $J_1\oplus J_2$
is
$J_1\oplus J_2$
is
![]() $J^{\prime }_1\oplus J^{\prime }_2$
. It is clear that
$J^{\prime }_1\oplus J^{\prime }_2$
. It is clear that
![]() ${\mathcal {N}}_{J^{\prime }_1}={\mathcal {N}}_{J_1}$
and
${\mathcal {N}}_{J^{\prime }_1}={\mathcal {N}}_{J_1}$
and
![]() ${\mathcal {N}}^*_{J^{\prime }_1}={\mathcal {N}}^*_{J_1}$
(by Theorem 2.15(c)).
${\mathcal {N}}^*_{J^{\prime }_1}={\mathcal {N}}^*_{J_1}$
(by Theorem 2.15(c)).
Recall that non-nearly coherent ideals must be non-meager (this also follows by Theorem 4.8), so
![]() $J^{\prime }_1\times J^{\prime }_2$
is a non-meager subset of
$J^{\prime }_1\times J^{\prime }_2$
is a non-meager subset of
![]() ${{}^\omega 2}= {}^{{\mathbb {N}}_1}2 \times {}^{{\mathbb {N}}_2}2$
by Kuratowski–Ulam Theorem, which implies that
${{}^\omega 2}= {}^{{\mathbb {N}}_1}2 \times {}^{{\mathbb {N}}_2}2$
by Kuratowski–Ulam Theorem, which implies that
![]() $J^{\prime }_1\oplus J^{\prime }_2$
is non-meager.
$J^{\prime }_1\oplus J^{\prime }_2$
is non-meager.
By Example 2.13,
![]() ${\mathcal {N}}^*_{J^{\prime }_1\oplus J^{\prime }_2}={\mathcal {N}}^*_{J^{\prime }_1}\cap {\mathcal {N}}^*_{J^{\prime }_2} = {\mathcal {N}}^*_{J_1}\cap {\mathcal {N}}^*_{J_2}$
and
${\mathcal {N}}^*_{J^{\prime }_1\oplus J^{\prime }_2}={\mathcal {N}}^*_{J^{\prime }_1}\cap {\mathcal {N}}^*_{J^{\prime }_2} = {\mathcal {N}}^*_{J_1}\cap {\mathcal {N}}^*_{J_2}$
and
![]() ${\mathcal {N}}_{J^{\prime }_1 \oplus J^{\prime }_2}$
contains both
${\mathcal {N}}_{J^{\prime }_1 \oplus J^{\prime }_2}$
contains both
![]() ${\mathcal {N}}_{J_1}$
and
${\mathcal {N}}_{J_1}$
and
![]() ${\mathcal {N}}_{J_2}$
, so
${\mathcal {N}}_{J_2}$
, so
![]() ${\mathcal {N}}^*_{J^{\prime }_1\oplus J^{\prime }_2}= {\mathcal {N}}_{J^{\prime }_1\oplus J^{\prime }_2}$
would imply that
${\mathcal {N}}^*_{J^{\prime }_1\oplus J^{\prime }_2}= {\mathcal {N}}_{J^{\prime }_1\oplus J^{\prime }_2}$
would imply that
![]() ${\mathcal {N}}_{J_1}\cup {\mathcal {N}}_{J_2}\subseteq {\mathcal {N}}^*_{J_1}\cap {\mathcal {N}}^*_{J_2}$
, and in turn
${\mathcal {N}}_{J_1}\cup {\mathcal {N}}_{J_2}\subseteq {\mathcal {N}}^*_{J_1}\cap {\mathcal {N}}^*_{J_2}$
, and in turn
![]() ${\mathcal {N}}_{J_2}\subseteq {\mathcal {N}}^*_{J_1}$
, which implies
${\mathcal {N}}_{J_2}\subseteq {\mathcal {N}}^*_{J_1}$
, which implies
![]() ${\mathcal {N}}^*_{J_2}\subseteq {\mathcal {N}}_{J_1}$
(because
${\mathcal {N}}^*_{J_2}\subseteq {\mathcal {N}}_{J_1}$
(because
![]() ${\mathcal {N}}^*_{J_e}\subseteq {\mathcal {N}}_{J_e}$
), contradicting Theorem 4.10 and the fact that
${\mathcal {N}}^*_{J_e}\subseteq {\mathcal {N}}_{J_e}$
), contradicting Theorem 4.10 and the fact that
![]() $J_1$
and
$J_1$
and
![]() $J_2$
are not nearly-coherent. Therefore,
$J_2$
are not nearly-coherent. Therefore,
![]() ${\mathcal {N}}^*_{J^{\prime }_1\oplus J^{\prime }_2}\neq {\mathcal {N}}_{J^{\prime }_1\oplus J^{\prime }_2}$
${\mathcal {N}}^*_{J^{\prime }_1\oplus J^{\prime }_2}\neq {\mathcal {N}}_{J^{\prime }_1\oplus J^{\prime }_2}$
In contrast with the previous result, we do not know whether NCF implies that all
![]() ${\mathcal {N}}_J$
are the same for non-meager J.
${\mathcal {N}}_J$
are the same for non-meager J.
5 Cardinal characteristics
In this section, we focus on investigating the cardinal characteristics associated with
![]() ${\mathcal {N}}_J$
and
${\mathcal {N}}_J$
and
![]() ${\mathcal {N}}^*_J$
.
${\mathcal {N}}^*_J$
.
We review some basic notation about cardinal characteristics. Many cardinal characteristics are defined using relational systems in the following way [Reference Vojtáš45]. A relational system is a triplet
![]() ${\mathbf {R}}=\langle X,Y,R\rangle $
where R is a relation and X and Y are non-empty sets.Footnote
6
Define
${\mathbf {R}}=\langle X,Y,R\rangle $
where R is a relation and X and Y are non-empty sets.Footnote
6
Define
 $$ \begin{align*} {\mathfrak{b}}({\mathbf{R}}) & :=\min{\left\{ |F| :\, F\subseteq X,\ \neg\,(\exists\, y\in Y)\ (\forall\, x\in F)\ x\, R\, y \right\}},\\ {\mathfrak{d}}({\mathbf{R}}) & :=\min{\left\{ |D| :\, D\subseteq Y,\ (\forall\, x\in X)\ (\exists\, y\in D)\ x\, R\, y \right\}}. \end{align*} $$
$$ \begin{align*} {\mathfrak{b}}({\mathbf{R}}) & :=\min{\left\{ |F| :\, F\subseteq X,\ \neg\,(\exists\, y\in Y)\ (\forall\, x\in F)\ x\, R\, y \right\}},\\ {\mathfrak{d}}({\mathbf{R}}) & :=\min{\left\{ |D| :\, D\subseteq Y,\ (\forall\, x\in X)\ (\exists\, y\in D)\ x\, R\, y \right\}}. \end{align*} $$
The dual of
![]() ${\mathbf {R}}$
is defined by
${\mathbf {R}}$
is defined by
![]() ${\mathbf {R}}^\perp :=\langle Y,X,R^\perp \rangle $
where
${\mathbf {R}}^\perp :=\langle Y,X,R^\perp \rangle $
where
![]() $y\, R^\perp \, x$
iff
$y\, R^\perp \, x$
iff
![]() $\neg \, x\, R\, y$
. Hence
$\neg \, x\, R\, y$
. Hence
![]() ${\mathfrak {b}}({\mathbf {R}}^\perp )={\mathfrak {d}}({\mathbf {R}})$
and
${\mathfrak {b}}({\mathbf {R}}^\perp )={\mathfrak {d}}({\mathbf {R}})$
and
![]() ${\mathfrak {d}}({\mathbf {R}}^\perp )={\mathfrak {b}}({\mathbf {R}})$
.
${\mathfrak {d}}({\mathbf {R}}^\perp )={\mathfrak {b}}({\mathbf {R}})$
.
Given another relational system
![]() ${\mathbf {R}}'=\langle X', Y', R'\rangle $
, say that a pair
${\mathbf {R}}'=\langle X', Y', R'\rangle $
, say that a pair
![]() $(\varphi _-,\varphi _+)$
is a Tukey connection from
$(\varphi _-,\varphi _+)$
is a Tukey connection from
![]() ${\mathbf {R}}$
to
${\mathbf {R}}$
to
![]() ${\mathbf {R}}'$
if
${\mathbf {R}}'$
if
![]() $\varphi _-:X\to X'$
,
$\varphi _-:X\to X'$
,
![]() $\varphi _+:Y'\to Y$
and, for any
$\varphi _+:Y'\to Y$
and, for any
![]() $x\in X$
and
$x\in X$
and
![]() $y'\in Y'$
, if
$y'\in Y'$
, if
![]() $\varphi _-(x)\, R'\, y'$
then
$\varphi _-(x)\, R'\, y'$
then
![]() $x\, R\, \varphi _+(y')$
.
$x\, R\, \varphi _+(y')$
.
We say that
![]() ${\mathbf {R}}$
is Tukey below
${\mathbf {R}}$
is Tukey below
![]() ${\mathbf {R}}'$
, denoted by
${\mathbf {R}}'$
, denoted by
![]() ${\mathbf {R}}{\mathrel {\preceq _{\mathrm {T}}}}{\mathbf {R}}'$
, if there is a Tukey connection from
${\mathbf {R}}{\mathrel {\preceq _{\mathrm {T}}}}{\mathbf {R}}'$
, if there is a Tukey connection from
![]() ${\mathbf {R}}$
to
${\mathbf {R}}$
to
![]() ${\mathbf {R}}'$
. Say that
${\mathbf {R}}'$
. Say that
![]() ${\mathbf {R}}$
is Tukey equivalent to
${\mathbf {R}}$
is Tukey equivalent to
![]() ${\mathbf {R}}'$
, denoted by
${\mathbf {R}}'$
, denoted by
![]() ${\mathbf {R}}{\mathrel {\cong _{\mathrm {T}}}}{\mathbf {R}}'$
, if
${\mathbf {R}}{\mathrel {\cong _{\mathrm {T}}}}{\mathbf {R}}'$
, if
![]() ${\mathbf {R}}{\mathrel {\preceq _{\mathrm {T}}}}{\mathbf {R}}'$
and
${\mathbf {R}}{\mathrel {\preceq _{\mathrm {T}}}}{\mathbf {R}}'$
and
![]() ${\mathbf {R}}'{\mathrel {\preceq _{\mathrm {T}}}}{\mathbf {R}}$
. It is known that
${\mathbf {R}}'{\mathrel {\preceq _{\mathrm {T}}}}{\mathbf {R}}$
. It is known that
![]() ${\mathbf {R}}{\mathrel {\preceq _{\mathrm {T}}}}{\mathbf {R}}'$
implies
${\mathbf {R}}{\mathrel {\preceq _{\mathrm {T}}}}{\mathbf {R}}'$
implies
![]() ${\mathfrak {d}}({\mathbf {R}})\leq {\mathfrak {d}}({\mathbf {R}}')$
and
${\mathfrak {d}}({\mathbf {R}})\leq {\mathfrak {d}}({\mathbf {R}}')$
and
![]() ${\mathfrak {b}}({\mathbf {R}}')\leq {\mathfrak {b}}({\mathbf {R}})$
. Hence
${\mathfrak {b}}({\mathbf {R}}')\leq {\mathfrak {b}}({\mathbf {R}})$
. Hence
![]() ${\mathbf {R}}{\mathrel {\cong _{\mathrm {T}}}}{\mathbf {R}}'$
implies
${\mathbf {R}}{\mathrel {\cong _{\mathrm {T}}}}{\mathbf {R}}'$
implies
![]() ${\mathfrak {d}}({\mathbf {R}})={\mathfrak {d}}({\mathbf {R}}')$
and
${\mathfrak {d}}({\mathbf {R}})={\mathfrak {d}}({\mathbf {R}}')$
and
![]() ${\mathfrak {b}}({\mathbf {R}}')={\mathfrak {b}}({\mathbf {R}})$
.
${\mathfrak {b}}({\mathbf {R}}')={\mathfrak {b}}({\mathbf {R}})$
.
We constantly use the relational system
![]() ${\mathbf {c}}^{\mathcal {J}}_{\mathcal {I}}:=\langle {\mathcal {I}},{\mathcal {J}},\subseteq \rangle $
discussed in [Reference Bartoszyński and Judah4, Chapter 2], and we identify
${\mathbf {c}}^{\mathcal {J}}_{\mathcal {I}}:=\langle {\mathcal {I}},{\mathcal {J}},\subseteq \rangle $
discussed in [Reference Bartoszyński and Judah4, Chapter 2], and we identify
![]() ${\mathcal {I}}$
with the relational system
${\mathcal {I}}$
with the relational system
![]() ${\mathbf {c}}^{\mathcal {I}}_{\mathcal {I}}$
. Denote
${\mathbf {c}}^{\mathcal {I}}_{\mathcal {I}}$
. Denote
![]() ${\mathrm {add}}({\mathcal {I}},{\mathcal {J}}):={\mathfrak {b}}({\mathbf {c}}^{\mathcal {J}}_{\mathcal {I}})$
and
${\mathrm {add}}({\mathcal {I}},{\mathcal {J}}):={\mathfrak {b}}({\mathbf {c}}^{\mathcal {J}}_{\mathcal {I}})$
and
![]() ${\mathrm {cof}}({\mathcal {I}},{\mathcal {J}}):={\mathfrak {d}}({\mathbf {c}}^{\mathcal {J}}_{\mathcal {I}})$
. These cardinal characteristics are interesting when
${\mathrm {cof}}({\mathcal {I}},{\mathcal {J}}):={\mathfrak {d}}({\mathbf {c}}^{\mathcal {J}}_{\mathcal {I}})$
. These cardinal characteristics are interesting when
![]() ${\mathcal {I}}\subseteq {\mathcal {J}}$
are ideals on some set X. It is well-known that, for any ideal
${\mathcal {I}}\subseteq {\mathcal {J}}$
are ideals on some set X. It is well-known that, for any ideal
![]() ${\mathcal {I}}$
on X, we can express the cardinal characteristics associated with
${\mathcal {I}}$
on X, we can express the cardinal characteristics associated with
![]() ${\mathcal {I}}$
as follows:
${\mathcal {I}}$
as follows:
 $$ \begin{align*} {\mathrm{add}}({\mathcal{I}})& ={\mathrm{add}}({\mathcal{I}},{\mathcal{I}}), & {\mathrm{cof}}({\mathcal{I}}) &={\mathrm{cof}}({\mathcal{I}},{\mathcal{I}}),\\ {\mathrm{non}}({\mathcal{I}})& ={\mathrm{add}}([X]^{<\aleph_0},{\mathcal{I}}), & {\mathrm{cov}}({\mathcal{I}})& ={\mathrm{cof}}([X]^{<\aleph_0},{\mathcal{I}}). \end{align*} $$
$$ \begin{align*} {\mathrm{add}}({\mathcal{I}})& ={\mathrm{add}}({\mathcal{I}},{\mathcal{I}}), & {\mathrm{cof}}({\mathcal{I}}) &={\mathrm{cof}}({\mathcal{I}},{\mathcal{I}}),\\ {\mathrm{non}}({\mathcal{I}})& ={\mathrm{add}}([X]^{<\aleph_0},{\mathcal{I}}), & {\mathrm{cov}}({\mathcal{I}})& ={\mathrm{cof}}([X]^{<\aleph_0},{\mathcal{I}}). \end{align*} $$
In fact, via the relational system
![]() ${\mathbf {C}}_{\mathcal {I}}:=\langle X,{\mathcal {I}},\in \rangle $
, we obtain
${\mathbf {C}}_{\mathcal {I}}:=\langle X,{\mathcal {I}},\in \rangle $
, we obtain
![]() ${\mathrm {non}}({\mathcal {I}})={\mathfrak {b}}({\mathbf {C}}_{\mathcal {I}})$
and
${\mathrm {non}}({\mathcal {I}})={\mathfrak {b}}({\mathbf {C}}_{\mathcal {I}})$
and
![]() ${\mathrm {cov}}({\mathcal {I}})={\mathfrak {d}}({\mathbf {C}}_{\mathcal {I}})$
. The following easy claims illustrate basic relations between these cardinal characteristics.
${\mathrm {cov}}({\mathcal {I}})={\mathfrak {d}}({\mathbf {C}}_{\mathcal {I}})$
. The following easy claims illustrate basic relations between these cardinal characteristics.
Fact 5.1. If
![]() ${\mathcal {I}}$
is an ideal on X,
${\mathcal {I}}$
is an ideal on X,
![]() ${\mathcal {I}}\subseteq {\mathcal {I}}'$
and
${\mathcal {I}}\subseteq {\mathcal {I}}'$
and
![]() ${\mathcal {J}}\subseteq {\mathcal {P}}(X)\smallsetminus \{X\}$
, then
${\mathcal {J}}\subseteq {\mathcal {P}}(X)\smallsetminus \{X\}$
, then
![]() $({\mathbf {c}}_{{\mathcal {I}}'}^{\mathcal {J}})^\perp\ {\mathrel {\preceq _{\mathrm {T}}}} {\mathbf {C}}_{\mathcal {I}}{\mathrel {\preceq _{\mathrm {T}}}}{\mathbf {c}}_{[X]^{<\aleph _0}}^{\mathcal {I}}$
. In particular,
$({\mathbf {c}}_{{\mathcal {I}}'}^{\mathcal {J}})^\perp\ {\mathrel {\preceq _{\mathrm {T}}}} {\mathbf {C}}_{\mathcal {I}}{\mathrel {\preceq _{\mathrm {T}}}}{\mathbf {c}}_{[X]^{<\aleph _0}}^{\mathcal {I}}$
. In particular,
![]() ${\mathrm {add}}({\mathcal {I}}',{\mathcal {J}})\leq {\mathrm {cov}}({\mathcal {I}})$
and
${\mathrm {add}}({\mathcal {I}}',{\mathcal {J}})\leq {\mathrm {cov}}({\mathcal {I}})$
and
![]() ${\mathrm {non}}({\mathcal {I}})\leq {\mathrm {cof}}({\mathcal {I}}',{\mathcal {J}})$
.
${\mathrm {non}}({\mathcal {I}})\leq {\mathrm {cof}}({\mathcal {I}}',{\mathcal {J}})$
.
Proof We only show the first Tukey connection. Define
![]() $F\colon {\mathcal {J}}\to X$
such that
$F\colon {\mathcal {J}}\to X$
such that
![]() $F(B)\in X\smallsetminus B$
(which exists because
$F(B)\in X\smallsetminus B$
(which exists because
![]() $X\notin {\mathcal {J}}$
), and define
$X\notin {\mathcal {J}}$
), and define
![]() $G\colon {\mathcal {I}}\to {\mathcal {I}}'$
by
$G\colon {\mathcal {I}}\to {\mathcal {I}}'$
by
![]() $G(A):=A$
. Then, for
$G(A):=A$
. Then, for
![]() $A\in {\mathcal {I}}$
and
$A\in {\mathcal {I}}$
and
![]() $B\in {\mathcal {J}}$
,
$B\in {\mathcal {J}}$
,
![]() $F(B)\in A$
implies
$F(B)\in A$
implies
![]() $B\nsupseteq A$
. Hence,
$B\nsupseteq A$
. Hence,
![]() $(F,G)$
witnesses
$(F,G)$
witnesses
![]() $({\mathbf {c}}_{{\mathcal {I}}'}^{\mathcal {J}})^\perp\ {\mathrel {\preceq _{\mathrm {T}}}}\ {\mathbf {C}}_{\mathcal {I}}$
.
$({\mathbf {c}}_{{\mathcal {I}}'}^{\mathcal {J}})^\perp\ {\mathrel {\preceq _{\mathrm {T}}}}\ {\mathbf {C}}_{\mathcal {I}}$
.
Fact 5.2. If
![]() ${\mathcal {I}}\subseteq {\mathcal {I}}'$
and
${\mathcal {I}}\subseteq {\mathcal {I}}'$
and
![]() ${\mathcal {J}}'\subseteq {\mathcal {J}}$
then
${\mathcal {J}}'\subseteq {\mathcal {J}}$
then
![]() ${\mathbf {c}}^{\mathcal {J}}_{\mathcal {I}}{\mathrel {\preceq _{\mathrm {T}}}} {\mathbf {c}}^{{\mathcal {J}}'}_{{\mathcal {I}}'}$
. In particular,
${\mathbf {c}}^{\mathcal {J}}_{\mathcal {I}}{\mathrel {\preceq _{\mathrm {T}}}} {\mathbf {c}}^{{\mathcal {J}}'}_{{\mathcal {I}}'}$
. In particular,
![]() ${\mathrm {add}}({\mathcal {I}}',{\mathcal {J}}')\leq {\mathrm {add}}({\mathcal {I}},{\mathcal {J}})$
and
${\mathrm {add}}({\mathcal {I}}',{\mathcal {J}}')\leq {\mathrm {add}}({\mathcal {I}},{\mathcal {J}})$
and
![]() ${\mathrm {cof}}({\mathcal {I}},{\mathcal {J}})\leq {\mathrm {cof}}({\mathcal {I}}',{\mathcal {J}}')$
.
${\mathrm {cof}}({\mathcal {I}},{\mathcal {J}})\leq {\mathrm {cof}}({\mathcal {I}}',{\mathcal {J}}')$
.
Corollary 5.3. If
![]() ${\mathcal {J}}'\subseteq {\mathcal {J}}$
are ideals on X, then
${\mathcal {J}}'\subseteq {\mathcal {J}}$
are ideals on X, then
![]() ${\mathbf {c}}^{{\mathcal {J}}}_{[X]^{<\aleph _0}} {\mathrel {\preceq _{\mathrm {T}}}} {\mathbf {c}}^{{\mathcal {J}}'}_{[X]^{<\aleph _0}}$
and
${\mathbf {c}}^{{\mathcal {J}}}_{[X]^{<\aleph _0}} {\mathrel {\preceq _{\mathrm {T}}}} {\mathbf {c}}^{{\mathcal {J}}'}_{[X]^{<\aleph _0}}$
and
![]() ${\mathbf {C}}_{{\mathcal {J}}}\ {\mathrel {\preceq _{\mathrm {T}}}}\ {\mathbf {C}}_{{\mathcal {J}}'}$
. In particular,
${\mathbf {C}}_{{\mathcal {J}}}\ {\mathrel {\preceq _{\mathrm {T}}}}\ {\mathbf {C}}_{{\mathcal {J}}'}$
. In particular,
![]() ${\mathrm {cov}}({\mathcal {J}})\leq {\mathrm {cov}}({\mathcal {J}}')$
and
${\mathrm {cov}}({\mathcal {J}})\leq {\mathrm {cov}}({\mathcal {J}}')$
and
![]() ${\mathrm {non}}({\mathcal {J}}')\leq {\mathrm {non}}({\mathcal {J}})$
.
${\mathrm {non}}({\mathcal {J}}')\leq {\mathrm {non}}({\mathcal {J}})$
.
We look at the cardinal characteristics associated with
![]() ${\mathcal {N}}_J$
and
${\mathcal {N}}_J$
and
![]() ${\mathcal {N}}^*_J$
when J is an ideal on
${\mathcal {N}}^*_J$
when J is an ideal on
![]() $\omega $
. If
$\omega $
. If
![]() ${J}$
has the Baire property then the cardinal characteristics associated with
${J}$
has the Baire property then the cardinal characteristics associated with
![]() $\mathcal {N}_{J}$
equal to those associated with
$\mathcal {N}_{J}$
equal to those associated with
![]() $\mathcal {N}$
because
$\mathcal {N}$
because
![]() ${\mathcal {N}}_J={\mathcal {N}}$
(Theorem 2.18). Moreover, since
${\mathcal {N}}_J={\mathcal {N}}$
(Theorem 2.18). Moreover, since
![]() ${\mathcal {N}}^*_J={\mathcal {E}}$
, the cardinal characteristics associated with
${\mathcal {N}}^*_J={\mathcal {E}}$
, the cardinal characteristics associated with
![]() ${\mathcal {N}^*_{J}}$
equal to those associated with
${\mathcal {N}^*_{J}}$
equal to those associated with
![]() $\mathcal {E}$
. We recall below some results about the cardinal characteristics associated with
$\mathcal {E}$
. We recall below some results about the cardinal characteristics associated with
![]() ${\mathcal {E}}$
.
${\mathcal {E}}$
.
Theorem 5.4 ([Reference Bartoszyński and Shelah6], see also [Reference Bartoszyński and Judah4, Section 2.6]).
-
(a)
 $\min \{{\mathfrak {b}},{\mathrm {non}}({\mathcal {N}})\} \leq {\mathrm {non}}({\mathcal {E}})\leq \min \{{\mathrm {non}}({\mathcal {M}}),{\mathrm {non}}({\mathcal {N}})\}$
.
$\min \{{\mathfrak {b}},{\mathrm {non}}({\mathcal {N}})\} \leq {\mathrm {non}}({\mathcal {E}})\leq \min \{{\mathrm {non}}({\mathcal {M}}),{\mathrm {non}}({\mathcal {N}})\}$
. -
(b)
 $\max \{{\mathrm {cov}}({\mathcal {M}}),{\mathrm {cov}}({\mathcal {N}})\}\leq {\mathrm {cov}}({\mathcal {E}}) \leq \max \{{\mathfrak {d}},{\mathrm {cov}}({\mathcal {N}})\}$
.
$\max \{{\mathrm {cov}}({\mathcal {M}}),{\mathrm {cov}}({\mathcal {N}})\}\leq {\mathrm {cov}}({\mathcal {E}}) \leq \max \{{\mathfrak {d}},{\mathrm {cov}}({\mathcal {N}})\}$
. -
(c)
 ${\mathrm {add}}({\mathcal {E}},{\mathcal {N}})={\mathrm {cov}}({\mathcal {M}})$
and
${\mathrm {add}}({\mathcal {E}},{\mathcal {N}})={\mathrm {cov}}({\mathcal {M}})$
and
 ${\mathrm {cof}}({\mathcal {E}},{\mathcal {N}})={\mathrm {non}}({\mathcal {M}})$
.
${\mathrm {cof}}({\mathcal {E}},{\mathcal {N}})={\mathrm {non}}({\mathcal {M}})$
. -
(d)
 ${\mathrm {add}}({\mathcal {E}})={\mathrm {add}}({\mathcal {M}})$
and
${\mathrm {add}}({\mathcal {E}})={\mathrm {add}}({\mathcal {M}})$
and
 ${\mathrm {cof}}({\mathcal {E}})={\mathrm {cof}}({\mathcal {M}})$
.
${\mathrm {cof}}({\mathcal {E}})={\mathrm {cof}}({\mathcal {M}})$
.
Theorem 5.5 [Reference Bartoszyński and Judah4, Lemma 7.4.3].
![]() ${\mathfrak {s}}\leq {\mathrm {non}}({\mathcal {E}})$
and
${\mathfrak {s}}\leq {\mathrm {non}}({\mathcal {E}})$
and
![]() ${\mathrm {cov}}({\mathcal {E}})\leq {\mathfrak {r}}$
.
${\mathrm {cov}}({\mathcal {E}})\leq {\mathfrak {r}}$
.
Thanks to the previous results, and the fact that
![]() ${\mathcal {E}}\subseteq {\mathcal {N}^*_{J}}\subseteq {\mathcal {N}_{J}}\subseteq \mathcal {N}$
, the inequalities below immediately follow.
${\mathcal {E}}\subseteq {\mathcal {N}^*_{J}}\subseteq {\mathcal {N}_{J}}\subseteq \mathcal {N}$
, the inequalities below immediately follow.
Theorem 5.6.
![]() $\mathrm {ZFC}$
proves
$\mathrm {ZFC}$
proves
We now turn to the additivity and cofinality numbers. In the case of
![]() $J={\mathrm {Fin}}$
, we can characterize
$J={\mathrm {Fin}}$
, we can characterize
![]() ${\mathrm {add}}({\mathcal {N}})$
and
${\mathrm {add}}({\mathcal {N}})$
and
![]() ${\mathrm {cof}}({\mathcal {N}})$
using slaloms.
${\mathrm {cof}}({\mathcal {N}})$
using slaloms.
Definition 5.7. Let
![]() $b=\langle b(n):\, n<\omega \rangle $
be a sequence of non-empty sets, and let
$b=\langle b(n):\, n<\omega \rangle $
be a sequence of non-empty sets, and let
![]() $h\in {{}^\omega \omega }$
. Denote
$h\in {{}^\omega \omega }$
. Denote
 $$ \begin{align*} \prod b & := \prod_{n<\omega}b(n),\\ {S}(b,h) & := \prod_{n<\omega}[b(n)]^{\leq h(n)}. \end{align*} $$
$$ \begin{align*} \prod b & := \prod_{n<\omega}b(n),\\ {S}(b,h) & := \prod_{n<\omega}[b(n)]^{\leq h(n)}. \end{align*} $$
Define the relational system
![]() ${\mathbf {Lc}}(b,h):=\langle \prod b, {S}(b,h), \in ^*\rangle $
where
${\mathbf {Lc}}(b,h):=\langle \prod b, {S}(b,h), \in ^*\rangle $
where
Denote
![]() $\mathfrak {b}^{\mathrm {Lc}}_{b,h}:={\mathfrak {b}}({\mathbf {Lc}}(b,h))$
and
$\mathfrak {b}^{\mathrm {Lc}}_{b,h}:={\mathfrak {b}}({\mathbf {Lc}}(b,h))$
and
![]() $\mathfrak {d}^{\mathrm {Lc}}_{b,h}:={\mathfrak {d}}({\mathbf {Lc}}(b,h))$
.
$\mathfrak {d}^{\mathrm {Lc}}_{b,h}:={\mathfrak {d}}({\mathbf {Lc}}(b,h))$
.
When b is the constant sequence
![]() $\omega $
, we use the notation
$\omega $
, we use the notation
![]() ${\mathbf {Lc}}(\omega ,h)$
and denote its associated cardinal characteristics by
${\mathbf {Lc}}(\omega ,h)$
and denote its associated cardinal characteristics by
![]() $\mathfrak {b}^{\mathrm {Lc}}_{\omega ,h}$
and
$\mathfrak {b}^{\mathrm {Lc}}_{\omega ,h}$
and
![]() $\mathfrak {d}^{\mathrm {Lc}}_{\omega ,h}$
.
$\mathfrak {d}^{\mathrm {Lc}}_{\omega ,h}$
.
Theorem 5.8 (Bartoszyński [Reference Bartoszyński2, Reference Bartoszynski3]).
Assume that
![]() $h\in {{}^\omega \omega }$
diverges to infinity. Then,
$h\in {{}^\omega \omega }$
diverges to infinity. Then,
![]() ${\mathbf {Lc}}(b,h){\mathrel {\cong _{\mathrm {T}}}} {\mathcal {N}}$
. In particular,
${\mathbf {Lc}}(b,h){\mathrel {\cong _{\mathrm {T}}}} {\mathcal {N}}$
. In particular,
![]() $\mathfrak {b}^{\mathrm {Lc}}_{\omega ,h}={\mathrm {add}}({\mathcal {N}})$
and
$\mathfrak {b}^{\mathrm {Lc}}_{\omega ,h}={\mathrm {add}}({\mathcal {N}})$
and
![]() $\mathfrak {d}^{\mathrm {Lc}}_{\omega ,h}={\mathrm {cof}}({\mathcal {N}})$
.
$\mathfrak {d}^{\mathrm {Lc}}_{\omega ,h}={\mathrm {cof}}({\mathcal {N}})$
.
We propose the following relational system, which is practical to find bounds for the additivity and cofinality of
![]() ${\mathcal {N}}_J$
and
${\mathcal {N}}_J$
and
![]() ${\mathcal {N}}^*_J$
.
${\mathcal {N}}^*_J$
.
Definition 5.9. Let J be an ideal on
![]() $\omega $
. For
$\omega $
. For
![]() $c,d\in {{\overline {\Omega }}}$
, define the relation
$c,d\in {{\overline {\Omega }}}$
, define the relation
Define the relational system
![]() ${\mathbf {S}}_J:=\langle {{\overline {\Omega }}}, {{\overline {\Omega }}}, \subseteq ^J\rangle $
, and denote
${\mathbf {S}}_J:=\langle {{\overline {\Omega }}}, {{\overline {\Omega }}}, \subseteq ^J\rangle $
, and denote
![]() ${\mathfrak {b}}_J({{\overline {\Omega }}}):={\mathfrak {b}}({\mathbf {S}}_J)$
and
${\mathfrak {b}}_J({{\overline {\Omega }}}):={\mathfrak {b}}({\mathbf {S}}_J)$
and
![]() ${\mathfrak {d}}_J({{\overline {\Omega }}}):={\mathfrak {d}}({\mathbf {S}}_J)$
.
${\mathfrak {d}}_J({{\overline {\Omega }}}):={\mathfrak {d}}({\mathbf {S}}_J)$
.
It is clear that
![]() ${\mathfrak {b}}_J({{\overline {\Omega }}})$
is regular and
${\mathfrak {b}}_J({{\overline {\Omega }}})$
is regular and
![]() ${\mathfrak {b}}_J({{\overline {\Omega }}})\leq {\mathrm {cf}}({\mathfrak {d}}_J({{\overline {\Omega }}}))\leq {\mathfrak {d}}_J({{\overline {\Omega }}})$
.
${\mathfrak {b}}_J({{\overline {\Omega }}})\leq {\mathrm {cf}}({\mathfrak {d}}_J({{\overline {\Omega }}}))\leq {\mathfrak {d}}_J({{\overline {\Omega }}})$
.
Theorem 5.10. Let J be an ideal on
![]() $\omega $
. Then
$\omega $
. Then
![]() ${\mathcal {N}}_J{\mathrel {\preceq _{\mathrm {T}}}} {\mathbf {S}}_J$
and
${\mathcal {N}}_J{\mathrel {\preceq _{\mathrm {T}}}} {\mathbf {S}}_J$
and
![]() ${\mathcal {N}}^*_J{\mathrel {\preceq _{\mathrm {T}}}} {\mathbf {S}}_J$
. In particular, the additivities and cofinalities of
${\mathcal {N}}^*_J{\mathrel {\preceq _{\mathrm {T}}}} {\mathbf {S}}_J$
. In particular, the additivities and cofinalities of
![]() ${\mathcal {N}}_J$
and
${\mathcal {N}}_J$
and
![]() ${\mathcal {N}}^*_J$
are between
${\mathcal {N}}^*_J$
are between
![]() ${\mathfrak {b}}_J({{\overline {\Omega }}})$
and
${\mathfrak {b}}_J({{\overline {\Omega }}})$
and
![]() ${\mathfrak {d}}_J({{\overline {\Omega }}})$
(see Figure 5).
${\mathfrak {d}}_J({{\overline {\Omega }}})$
(see Figure 5).

Figure 5 Diagram of inequalities between the cardinal characteristics associated with
![]() ${\mathbf {S}}_J$
, and the additivities and cofinalities of
${\mathbf {S}}_J$
, and the additivities and cofinalities of
![]() ${\mathcal {N}}_J$
and
${\mathcal {N}}_J$
and
![]() ${\mathcal {N}}^*_J$
.
${\mathcal {N}}^*_J$
.
Proof Define
![]() $F\colon {\mathcal {N}}_J\to {{\overline {\Omega }}}$
such that
$F\colon {\mathcal {N}}_J\to {{\overline {\Omega }}}$
such that
![]() $X\subseteq N_J(F(X))$
for any
$X\subseteq N_J(F(X))$
for any
![]() $X\in {\mathcal {N}}_J$
, and define
$X\in {\mathcal {N}}_J$
, and define
![]() $G\colon {{\overline {\Omega }}} \to {\mathcal {N}}_J$
by
$G\colon {{\overline {\Omega }}} \to {\mathcal {N}}_J$
by
![]() $G(\bar d):=N_J(\bar d)$
for any
$G(\bar d):=N_J(\bar d)$
for any
![]() $\bar d\in {{\overline {\Omega }}}$
. It is clear that
$\bar d\in {{\overline {\Omega }}}$
. It is clear that
![]() $(F,G)$
is a Tukey connection from
$(F,G)$
is a Tukey connection from
![]() ${\mathcal {N}}_J$
into
${\mathcal {N}}_J$
into
![]() ${\mathbf {S}}_J$
, because
${\mathbf {S}}_J$
, because
![]() $\bar c\subseteq ^J \bar d$
implies
$\bar c\subseteq ^J \bar d$
implies
![]() $N_J(\bar c)\subseteq N_J(\bar d)$
.
$N_J(\bar c)\subseteq N_J(\bar d)$
.
Similarly, we obtain a Tukey connection from
![]() ${\mathcal {N}}^*_J$
into
${\mathcal {N}}^*_J$
into
![]() ${\mathbf {S}}_J$
via functions
${\mathbf {S}}_J$
via functions
![]() $F^*\colon {\mathcal {N}}^*_J\to {{\overline {\Omega }}}$
and
$F^*\colon {\mathcal {N}}^*_J\to {{\overline {\Omega }}}$
and
![]() $G^*\colon {{\overline {\Omega }}} \to {\mathcal {N}}_J$
such that
$G^*\colon {{\overline {\Omega }}} \to {\mathcal {N}}_J$
such that
![]() $X\subseteq N^*_J(F^*(X))$
for
$X\subseteq N^*_J(F^*(X))$
for
![]() $X\in {\mathcal {N}}^*_J$
and
$X\in {\mathcal {N}}^*_J$
and
![]() $G^*(\bar d):= N^*_J(\bar d)$
.
$G^*(\bar d):= N^*_J(\bar d)$
.
Analogous to Theorem 2.15, we have the following result about
![]() ${\mathbf {S}}_J$
.
${\mathbf {S}}_J$
.
Theorem 5.11. Let J and K be ideals on
![]() $\omega $
.
$\omega $
.
-
(a) If
 $K{\mathrel {\leq _{\mathrm {KB}}}} J$
, then
$K{\mathrel {\leq _{\mathrm {KB}}}} J$
, then
 ${\mathbf {S}}_J{\mathrel {\preceq _{\mathrm {T}}}} {\mathbf {S}}_K$
, in particular
${\mathbf {S}}_J{\mathrel {\preceq _{\mathrm {T}}}} {\mathbf {S}}_K$
, in particular
 ${\mathfrak {b}}_K({{\overline {\Omega }}})\leq {\mathfrak {b}}_J({{\overline {\Omega }}})$
and
${\mathfrak {b}}_K({{\overline {\Omega }}})\leq {\mathfrak {b}}_J({{\overline {\Omega }}})$
and
 ${\mathfrak {d}}_J({{\overline {\Omega }}})\leq {\mathfrak {d}}_K({{\overline {\Omega }}})$
.
${\mathfrak {d}}_J({{\overline {\Omega }}})\leq {\mathfrak {d}}_K({{\overline {\Omega }}})$
. -
(b) If
 $K {\mathrel {\leq _{\overline {\mathrm {KB}}}}} J$
, then
$K {\mathrel {\leq _{\overline {\mathrm {KB}}}}} J$
, then
 ${\mathbf {S}}_J{\mathrel {\preceq _{\mathrm {T}}}} {\mathbf {S}}_K$
, in particular
${\mathbf {S}}_J{\mathrel {\preceq _{\mathrm {T}}}} {\mathbf {S}}_K$
, in particular
 ${\mathfrak {b}}_K({{\overline {\Omega }}})\leq {\mathfrak {b}}_J({{\overline {\Omega }}})$
and
${\mathfrak {b}}_K({{\overline {\Omega }}})\leq {\mathfrak {b}}_J({{\overline {\Omega }}})$
and
 ${\mathfrak {d}}_J({{\overline {\Omega }}})\leq {\mathfrak {d}}_K({{\overline {\Omega }}})$
.
${\mathfrak {d}}_J({{\overline {\Omega }}})\leq {\mathfrak {d}}_K({{\overline {\Omega }}})$
. -
(c) If
 $K {\mathrel {\leq _{\mathrm {RB}}}} J$
, then
$K {\mathrel {\leq _{\mathrm {RB}}}} J$
, then
 ${\mathbf {S}}_K{\mathrel {\cong _{\mathrm {T}}}} {\mathbf {S}}_J$
, in particular
${\mathbf {S}}_K{\mathrel {\cong _{\mathrm {T}}}} {\mathbf {S}}_J$
, in particular
 ${\mathfrak {b}}_K({{\overline {\Omega }}}) ={\mathfrak {b}}_J({{\overline {\Omega }}})$
and
${\mathfrak {b}}_K({{\overline {\Omega }}}) ={\mathfrak {b}}_J({{\overline {\Omega }}})$
and
 ${\mathfrak {d}}_K({{\overline {\Omega }}}) = {\mathfrak {d}}_J({{\overline {\Omega }}})$
.
${\mathfrak {d}}_K({{\overline {\Omega }}}) = {\mathfrak {d}}_J({{\overline {\Omega }}})$
.
Proof It is clear that (c) follows from (a) and (b).
Let
![]() $f\colon \omega \to \omega $
be a finite-to-one function and denote
$f\colon \omega \to \omega $
be a finite-to-one function and denote
![]() $I_n:=f^{-1}[\{n\}]$
. Like in the proof of Theorem 2.15, define
$I_n:=f^{-1}[\{n\}]$
. Like in the proof of Theorem 2.15, define
![]() $F'\colon {{\overline {\Omega }}}\to {{\overline {\Omega }}}$
by
$F'\colon {{\overline {\Omega }}}\to {{\overline {\Omega }}}$
by
![]() $F'(\bar c):=\bar c'$
where
$F'(\bar c):=\bar c'$
where
![]() $c^{\prime }_n:=\bigcup _{k\in I_n}c_k$
, and define
$c^{\prime }_n:=\bigcup _{k\in I_n}c_k$
, and define
![]() $F^-\colon {{\overline {\Omega }}}\to {{\overline {\Omega }}}$
by
$F^-\colon {{\overline {\Omega }}}\to {{\overline {\Omega }}}$
by
![]() $F^-(\bar c):=\bar c^-$
where
$F^-(\bar c):=\bar c^-$
where
![]() $c^-_k:=c_{f(k)}$
.
$c^-_k:=c_{f(k)}$
.
If
![]() $K\subseteq f^{\to }(J)$
then
$K\subseteq f^{\to }(J)$
then
![]() $(F',F^-)$
is a Tukey connection from
$(F',F^-)$
is a Tukey connection from
![]() ${\mathbf {S}}_J$
into
${\mathbf {S}}_J$
into
![]() ${\mathbf {S}}_K$
, which shows (a). To prove this, assume
${\mathbf {S}}_K$
, which shows (a). To prove this, assume
![]() $\bar c,\bar d\in {{\overline {\Omega }}}$
and
$\bar c,\bar d\in {{\overline {\Omega }}}$
and
![]() $\bar c'\subseteq ^K \bar d$
, and we show
$\bar c'\subseteq ^K \bar d$
, and we show
![]() $\bar c \subseteq ^J \bar d^-$
. The hypothesis indicates that
$\bar c \subseteq ^J \bar d^-$
. The hypothesis indicates that
![]() ${\left \{ n<\omega :\, c^{\prime }_n\subseteq d_n \right \}}\in K^d$
, which implies that
${\left \{ n<\omega :\, c^{\prime }_n\subseteq d_n \right \}}\in K^d$
, which implies that
![]() ${\left \{ {k<\omega } :\, {c^{\prime }_{f(k)}\subseteq d_{f(k)}} \right \}}\in J^d$
. Since
${\left \{ {k<\omega } :\, {c^{\prime }_{f(k)}\subseteq d_{f(k)}} \right \}}\in J^d$
. Since
![]() $c_k\subseteq c^{\prime }_{f(k)}$
, the previous set is contained in
$c_k\subseteq c^{\prime }_{f(k)}$
, the previous set is contained in
![]() ${\left \{ k<\omega :\, c_k\subseteq d^-_k \right \}}$
, so
${\left \{ k<\omega :\, c_k\subseteq d^-_k \right \}}$
, so
![]() $\bar c \subseteq ^J \bar d^-$
.
$\bar c \subseteq ^J \bar d^-$
.
To show (b), we verify that, whenever
![]() $f^\to (K)\subseteq J$
,
$f^\to (K)\subseteq J$
,
![]() $(F^-,F')$
is a Tukey connection from
$(F^-,F')$
is a Tukey connection from
![]() ${\mathbf {S}}_J$
into
${\mathbf {S}}_J$
into
![]() ${\mathbf {S}}_K$
. Let
${\mathbf {S}}_K$
. Let
![]() $\bar c,\bar d\in {{\overline {\Omega }}}$
and assume that
$\bar c,\bar d\in {{\overline {\Omega }}}$
and assume that
![]() $\bar c^-\subseteq ^K \bar d$
, i.e.,
$\bar c^-\subseteq ^K \bar d$
, i.e.,
![]() ${\left \{ {k<\omega } :\, {c_{f(k)}\subseteq d_k} \right \}}\in K^d$
. Since
${\left \{ {k<\omega } :\, {c_{f(k)}\subseteq d_k} \right \}}\in K^d$
. Since
![]() $d_k\subseteq d^{\prime }_{f(k)}$
, this set is contained in
$d_k\subseteq d^{\prime }_{f(k)}$
, this set is contained in
![]() ${\left \{ {k<\omega } :\, {c_{f(k)}\subseteq d^{\prime }_{f(k)}} \right \}}$
, so
${\left \{ {k<\omega } :\, {c_{f(k)}\subseteq d^{\prime }_{f(k)}} \right \}}$
, so
![]() ${\left \{ n<\omega :\, c_n\subseteq d^{\prime }_n \right \}}\in J^d$
, i.e.,
${\left \{ n<\omega :\, c_n\subseteq d^{\prime }_n \right \}}\in J^d$
, i.e.,
![]() $\bar c\subseteq ^J \bar d'$
.
$\bar c\subseteq ^J \bar d'$
.
In the case
![]() $J={\mathrm {Fin}}$
, we obtain the following characterization of the additivity and cofinality of
$J={\mathrm {Fin}}$
, we obtain the following characterization of the additivity and cofinality of
![]() ${\mathcal {N}}$
.
${\mathcal {N}}$
.
Theorem 5.12.
![]() ${\mathfrak {b}}_{\mathrm {Fin}}({{\overline {\Omega }}})={\mathrm {add}}({\mathcal {N}})$
and
${\mathfrak {b}}_{\mathrm {Fin}}({{\overline {\Omega }}})={\mathrm {add}}({\mathcal {N}})$
and
![]() ${\mathfrak {d}}_{\mathrm {Fin}}({{\overline {\Omega }}})={\mathrm {cof}}({\mathcal {N}})$
.
${\mathfrak {d}}_{\mathrm {Fin}}({{\overline {\Omega }}})={\mathrm {cof}}({\mathcal {N}})$
.
Proof Note that
![]() ${\mathcal {N}}={\mathcal {N}}_{\mathrm {Fin}}{\mathrel {\preceq _{\mathrm {T}}}} {\mathbf {S}}_{\mathrm {Fin}}$
by Theorem 5.10, so
${\mathcal {N}}={\mathcal {N}}_{\mathrm {Fin}}{\mathrel {\preceq _{\mathrm {T}}}} {\mathbf {S}}_{\mathrm {Fin}}$
by Theorem 5.10, so
![]() ${\mathfrak {b}}_{\mathrm {Fin}}({{\overline {\Omega }}})\leq {\mathrm {add}}({\mathcal {N}})$
and
${\mathfrak {b}}_{\mathrm {Fin}}({{\overline {\Omega }}})\leq {\mathrm {add}}({\mathcal {N}})$
and
![]() ${\mathrm {cof}}({\mathcal {N}})\leq {\mathfrak {d}}_{\mathrm {Fin}}({{\overline {\Omega }}})$
.
${\mathrm {cof}}({\mathcal {N}})\leq {\mathfrak {d}}_{\mathrm {Fin}}({{\overline {\Omega }}})$
.
We show the converse inequality for
![]() ${\mathrm {add}}({\mathcal {N}})$
. It is enough to prove that, whenever
${\mathrm {add}}({\mathcal {N}})$
. It is enough to prove that, whenever
![]() $F\subseteq {{\overline {\Omega }}}$
has size
$F\subseteq {{\overline {\Omega }}}$
has size
![]() ${<}{\mathrm {add}}({\mathcal {N}})$
, it has some upper
${<}{\mathrm {add}}({\mathcal {N}})$
, it has some upper
![]() $\subseteq ^{\mathrm {Fin}}$
-bound. For each
$\subseteq ^{\mathrm {Fin}}$
-bound. For each
![]() $\bar c\in F$
, find a function
$\bar c\in F$
, find a function
![]() $f^{\bar c}\in {{}^\omega \omega }$
such that
$f^{\bar c}\in {{}^\omega \omega }$
such that
![]() $\mu \big (\bigcup _{k\geq f^{\bar c}(n)}c_k\big )<\frac {1}{(n+1)2^n}$
for all
$\mu \big (\bigcup _{k\geq f^{\bar c}(n)}c_k\big )<\frac {1}{(n+1)2^n}$
for all
![]() $n<\omega $
. Now
$n<\omega $
. Now
![]() $|F|<{\mathrm {add}}({\mathcal {N}})\leq {\mathfrak {b}}$
, so there is some increasing
$|F|<{\mathrm {add}}({\mathcal {N}})\leq {\mathfrak {b}}$
, so there is some increasing
![]() $f\in {{}^\omega \omega }$
with
$f\in {{}^\omega \omega }$
with
![]() $f(0)=0$
dominating
$f(0)=0$
dominating
![]() ${\left \{ f^{\bar c} :\, \bar c\in F \right \}}$
, which means that, for any
${\left \{ f^{\bar c} :\, \bar c\in F \right \}}$
, which means that, for any
![]() $\bar c\in F$
,
$\bar c\in F$
,
![]() $\mu \big (\bigcup _{k\geq f(n)}c_k\big )<\frac {1}{(n+1)2^n}$
for all but finitely many
$\mu \big (\bigcup _{k\geq f(n)}c_k\big )<\frac {1}{(n+1)2^n}$
for all but finitely many
![]() $n<\omega $
. By making finitely many modifications to each
$n<\omega $
. By making finitely many modifications to each
![]() $\bar c\in F$
, we can assume that the previous inequality is valid for all
$\bar c\in F$
, we can assume that the previous inequality is valid for all
![]() $n<\omega $
.
$n<\omega $
.
For each
![]() $n<\omega $
, let
$n<\omega $
, let
![]() $I_n:=[f(n),f(n+1))$
. Consider the functions
$I_n:=[f(n),f(n+1))$
. Consider the functions
![]() $b^f$
and h with domain
$b^f$
and h with domain
![]() $\omega $
such that
$\omega $
such that
![]() $b^f(n){\kern-1pt}:={\kern-1pt}{\left \{ {s\in {}^{I_n}\Omega } :\, {\mu \left ( \bigcup _{k\in I_n}s_k\right ){\kern-1pt}<{\kern-1pt}\frac {1}{(n+1)2^n}} \right \}}$
and
$b^f(n){\kern-1pt}:={\kern-1pt}{\left \{ {s\in {}^{I_n}\Omega } :\, {\mu \left ( \bigcup _{k\in I_n}s_k\right ){\kern-1pt}<{\kern-1pt}\frac {1}{(n+1)2^n}} \right \}}$
and
![]() $h(n){\kern-1pt}:={\kern-1pt}n+1$
. Since
$h(n){\kern-1pt}:={\kern-1pt}n+1$
. Since
![]() ${\mathbf {Lc}}(b^f,h){\mathrel {\cong _{\mathrm {T}}}} {\mathbf {Lc}}(\omega ,h){\mathrel {\cong _{\mathrm {T}}}} {\mathcal {N}}$
, we obtain that
${\mathbf {Lc}}(b^f,h){\mathrel {\cong _{\mathrm {T}}}} {\mathbf {Lc}}(\omega ,h){\mathrel {\cong _{\mathrm {T}}}} {\mathcal {N}}$
, we obtain that
![]() $\mathfrak {b}^{\mathrm {Lc}}_{b^f,h}={\mathrm {add}}({\mathcal {N}})$
by Theorem 5.8. Since F can be seen as a subset of
$\mathfrak {b}^{\mathrm {Lc}}_{b^f,h}={\mathrm {add}}({\mathcal {N}})$
by Theorem 5.8. Since F can be seen as a subset of
![]() $\prod b^f$
, there is some
$\prod b^f$
, there is some
![]() $\varphi \in {S}(b^f,h)$
such that, for any
$\varphi \in {S}(b^f,h)$
such that, for any
![]() $\bar c\in F$
,
$\bar c\in F$
,
![]() $\bar c\upharpoonright I_n\in \varphi (n)$
for all but finitely many
$\bar c\upharpoonright I_n\in \varphi (n)$
for all but finitely many
![]() $n<\omega $
. Define
$n<\omega $
. Define
![]() $\bar d\in {}^\omega \Omega $
by
$\bar d\in {}^\omega \Omega $
by
![]() $d_k:=\bigcup _{s\in \varphi (n)}s_k$
for
$d_k:=\bigcup _{s\in \varphi (n)}s_k$
for
![]() $k\in I_n$
. Note that
$k\in I_n$
. Note that
 $$ \begin{align*}\mu\left(\bigcup_{k\in I_n}d_k\right) = \mu\left( \bigcup_{s\in\varphi(n)} \bigcup_{k\in I_n}s_k\right)<\frac{1}{(n+1)2^n}(n+1)=\frac{1}{2^n},\end{align*} $$
$$ \begin{align*}\mu\left(\bigcup_{k\in I_n}d_k\right) = \mu\left( \bigcup_{s\in\varphi(n)} \bigcup_{k\in I_n}s_k\right)<\frac{1}{(n+1)2^n}(n+1)=\frac{1}{2^n},\end{align*} $$
thus
![]() $\bar d\in {{\overline {\Omega }}}$
. On the other hand, for any
$\bar d\in {{\overline {\Omega }}}$
. On the other hand, for any
![]() $\bar c\in F$
,
$\bar c\in F$
,
![]() $c_k\subseteq d_k$
for all but finitely many
$c_k\subseteq d_k$
for all but finitely many
![]() $k<\omega $
, i.e.,
$k<\omega $
, i.e.,
![]() $\bar c\subseteq ^{\mathrm {Fin}} \bar d$
.
$\bar c\subseteq ^{\mathrm {Fin}} \bar d$
.
The proof of
![]() ${\mathfrak {d}}_{\mathrm {Fin}}({{\overline {\Omega }}})\leq {\mathrm {cof}}({\mathcal {N}})$
is similar. Fix a dominating family D of size
${\mathfrak {d}}_{\mathrm {Fin}}({{\overline {\Omega }}})\leq {\mathrm {cof}}({\mathcal {N}})$
is similar. Fix a dominating family D of size
![]() ${\mathfrak {d}}$
formed by increasing functions f such that
${\mathfrak {d}}$
formed by increasing functions f such that
![]() $f(0)=0$
. For each
$f(0)=0$
. For each
![]() $f\in D$
, note that
$f\in D$
, note that
![]() $\mathfrak {d}^{\mathrm {Lc}}_{b^f,h}={\mathrm {cof}}({\mathcal {N}})$
by Theorem 5.8, so we can choose some witness
$\mathfrak {d}^{\mathrm {Lc}}_{b^f,h}={\mathrm {cof}}({\mathcal {N}})$
by Theorem 5.8, so we can choose some witness
![]() $S^f\subseteq {S}(b^f,h)$
and, for each
$S^f\subseteq {S}(b^f,h)$
and, for each
![]() $\varphi \in S^f$
, define
$\varphi \in S^f$
, define
![]() $d^{f,\varphi }_k:=\bigcup _{s\in \varphi (n)}s_k$
for
$d^{f,\varphi }_k:=\bigcup _{s\in \varphi (n)}s_k$
for
![]() $k\in [f(n),f(n+1))$
. Then,
$k\in [f(n),f(n+1))$
. Then,
![]() $E:={\left \{ \bar d^{f,\varphi } :\, \varphi ^f\in S^f,\ f\in D \right \}}$
has size
$E:={\left \{ \bar d^{f,\varphi } :\, \varphi ^f\in S^f,\ f\in D \right \}}$
has size
![]() ${\leq }{\mathrm {cof}}({\mathcal {N}})$
and it is
${\leq }{\mathrm {cof}}({\mathcal {N}})$
and it is
![]() ${\mathbf {S}}_{\mathrm {Fin}}$
-dominating, i.e., any
${\mathbf {S}}_{\mathrm {Fin}}$
-dominating, i.e., any
![]() $\bar c\in {{\overline {\Omega }}}$
is
$\bar c\in {{\overline {\Omega }}}$
is
![]() $\subseteq ^{\mathrm {Fin}}$
-bounded by some
$\subseteq ^{\mathrm {Fin}}$
-bounded by some
![]() $\bar d\in E$
.
$\bar d\in E$
.
Corollary 5.13. The additivities of
![]() ${\mathcal {N}}_J$
and
${\mathcal {N}}_J$
and
![]() ${\mathcal {N}}^*_J$
are between
${\mathcal {N}}^*_J$
are between
![]() ${\mathrm {add}}({\mathcal {N}})$
and
${\mathrm {add}}({\mathcal {N}})$
and
![]() ${\mathrm {cov}}({\mathcal {M}})$
(at the bottom of Cichoń’s diagram)
${\mathrm {cov}}({\mathcal {M}})$
(at the bottom of Cichoń’s diagram)
![]() $;$
the cofinalities of
$;$
the cofinalities of
![]() ${\mathcal {N}}_J$
and
${\mathcal {N}}_J$
and
![]() ${\mathcal {N}}^*_J$
are between
${\mathcal {N}}^*_J$
are between
![]() ${\mathrm {non}}({\mathcal {M}})$
and
${\mathrm {non}}({\mathcal {M}})$
and
![]() ${\mathrm {cof}}({\mathcal {N}})$
(at the top of Cichoń’s diagram).
${\mathrm {cof}}({\mathcal {N}})$
(at the top of Cichoń’s diagram).
Proof Since
![]() ${\mathrm {Fin}}\ {\mathrel {\leq _{\mathrm {KB}}}}\ J$
, by Theorem 5.11 we obtain that
${\mathrm {Fin}}\ {\mathrel {\leq _{\mathrm {KB}}}}\ J$
, by Theorem 5.11 we obtain that
![]() ${\mathfrak {b}}_{\mathrm {Fin}}({{\overline {\Omega }}})\leq {\mathfrak {b}}_J({{\overline {\Omega }}})$
and
${\mathfrak {b}}_{\mathrm {Fin}}({{\overline {\Omega }}})\leq {\mathfrak {b}}_J({{\overline {\Omega }}})$
and
![]() ${\mathfrak {d}}_J({{\overline {\Omega }}})\leq {\mathfrak {d}}_J({{\overline {\Omega }}})$
. Hence, by Theorems 5.10 and 5.12, we obtain
${\mathfrak {d}}_J({{\overline {\Omega }}})\leq {\mathfrak {d}}_J({{\overline {\Omega }}})$
. Hence, by Theorems 5.10 and 5.12, we obtain
 $$ \begin{align*} {\mathrm{add}}({\mathcal{N}})\leq &\ {\mathfrak{b}}_J({{\overline{\Omega}}})\leq \min\{{\mathrm{add}}({\mathcal{N}}_J),{\mathrm{add}}({\mathcal{N}}^*_J)\} \mbox{ and }\\ \max\{{\mathrm{cof}}({\mathcal{N}}_J),{\mathrm{cof}}({\mathcal{N}}^*_J)\}\leq &\ {\mathfrak{d}}_J({{\overline{\Omega}}})\leq {\mathrm{cof}}({\mathcal{N}}). \end{align*} $$
$$ \begin{align*} {\mathrm{add}}({\mathcal{N}})\leq &\ {\mathfrak{b}}_J({{\overline{\Omega}}})\leq \min\{{\mathrm{add}}({\mathcal{N}}_J),{\mathrm{add}}({\mathcal{N}}^*_J)\} \mbox{ and }\\ \max\{{\mathrm{cof}}({\mathcal{N}}_J),{\mathrm{cof}}({\mathcal{N}}^*_J)\}\leq &\ {\mathfrak{d}}_J({{\overline{\Omega}}})\leq {\mathrm{cof}}({\mathcal{N}}). \end{align*} $$
On the other hand, by Fact 5.2 and Theorem 5.4,
![]() ${\mathrm {add}}({\mathcal {N}}_J)={\mathrm {add}}({\mathcal {N}}_J,{\mathcal {N}}_J)\leq {\mathrm {add}}({\mathcal {E}},{\mathcal {N}})={\mathrm {cov}}({\mathcal {M}})$
and
${\mathrm {add}}({\mathcal {N}}_J)={\mathrm {add}}({\mathcal {N}}_J,{\mathcal {N}}_J)\leq {\mathrm {add}}({\mathcal {E}},{\mathcal {N}})={\mathrm {cov}}({\mathcal {M}})$
and
![]() ${\mathrm {non}}({\mathcal {M}})= {\mathrm {cof}}({\mathcal {E}},{\mathcal {N}}) \leq {\mathrm {cof}}({\mathcal {N}}_J,{\mathcal {N}}_J)={\mathrm {cof}}({\mathcal {N}}_J)$
, likewise for
${\mathrm {non}}({\mathcal {M}})= {\mathrm {cof}}({\mathcal {E}},{\mathcal {N}}) \leq {\mathrm {cof}}({\mathcal {N}}_J,{\mathcal {N}}_J)={\mathrm {cof}}({\mathcal {N}}_J)$
, likewise for
![]() ${\mathcal {N}}^*_J$
.
${\mathcal {N}}^*_J$
.
6 Consistency results
We show the behaviour of the cardinal characteristics associated with
![]() ${\mathcal {N}}_J$
and
${\mathcal {N}}_J$
and
![]() ${\mathcal {N}}^*_J$
in different forcing models. As usual, we start with the Cohen model, where the behaviour of these cardinal characteristics are similar to
${\mathcal {N}}^*_J$
in different forcing models. As usual, we start with the Cohen model, where the behaviour of these cardinal characteristics are similar to
![]() ${\mathfrak {b}}_J$
and
${\mathfrak {b}}_J$
and
![]() ${\mathfrak {d}}_J$
, in the sense of [Reference Canjar18]. Inspired by this reference, we present the following effect of adding a single Cohen real.
${\mathfrak {d}}_J$
, in the sense of [Reference Canjar18]. Inspired by this reference, we present the following effect of adding a single Cohen real.
Lemma 6.1. Cohen forcing
![]() ${\mathbb {C}}$
adds a real
${\mathbb {C}}$
adds a real
![]() $\bar e\in {{\overline {\Omega }}}$
such that, for any ideal J on
$\bar e\in {{\overline {\Omega }}}$
such that, for any ideal J on
![]() $\omega $
in the ground model, there is some ideal
$\omega $
in the ground model, there is some ideal
![]() $J'\supseteq J$
on
$J'\supseteq J$
on
![]() $\omega $
in the generic extension, such that
$\omega $
in the generic extension, such that
![]() $\bar c\subseteq ^{J'} \bar e$
for any
$\bar c\subseteq ^{J'} \bar e$
for any
![]() $\bar c\in {{\overline {\Omega }}}$
in the ground model.
$\bar c\in {{\overline {\Omega }}}$
in the ground model.
Proof Consider Cohen forcing
![]() ${\mathbb {C}}$
as the poset formed by pairs of finite sequences
${\mathbb {C}}$
as the poset formed by pairs of finite sequences
![]() $p=(n^p,c^p)$
such that
$p=(n^p,c^p)$
such that
![]() $n^p=\langle n^p_k:\, k<m \rangle $
is an increasing sequence of natural numbers,
$n^p=\langle n^p_k:\, k<m \rangle $
is an increasing sequence of natural numbers,
![]() $c^p= \langle c^p_i :\, i<n^p_{m-1}\rangle $
is a sequence of clopen subsets of
$c^p= \langle c^p_i :\, i<n^p_{m-1}\rangle $
is a sequence of clopen subsets of
![]() ${{}^\omega 2}$
and
${{}^\omega 2}$
and
 $$ \begin{align} \mu\left(\bigcup_{i=n^p_k}^{n^p_{k+1}-1} c^p_i\right)<2^{-(k+1)} \end{align} $$
$$ \begin{align} \mu\left(\bigcup_{i=n^p_k}^{n^p_{k+1}-1} c^p_i\right)<2^{-(k+1)} \end{align} $$
for any
![]() $k<m-1$
. The order is
$k<m-1$
. The order is
![]() $q\leq p$
iff
$q\leq p$
iff
![]() $n^q$
end-extends
$n^q$
end-extends
![]() $n^p$
and
$n^p$
and
![]() $c^q$
end-extends
$c^q$
end-extends
![]() $c^p$
. If G is
$c^p$
. If G is
![]() ${\mathbb {C}}$
-generic over the ground model V, we define
${\mathbb {C}}$
-generic over the ground model V, we define
![]() $\bar e$
by
$\bar e$
by
![]() $e_k:=c^p_k$
for some
$e_k:=c^p_k$
for some
![]() $p\in G$
(this value does not depend on such a p). It is easy to show that
$p\in G$
(this value does not depend on such a p). It is easy to show that
![]() $\bar e \in {{\overline {\Omega }}}$
.
$\bar e \in {{\overline {\Omega }}}$
.
It is enough to show that, in the Cohen extension,
i.e.,
![]() $\omega $
cannot be covered by finitely many members of that collection. Then, the promised
$\omega $
cannot be covered by finitely many members of that collection. Then, the promised
![]() $J'$
will be the ideal generated by this collection.
$J'$
will be the ideal generated by this collection.
So, in the ground model, fix
![]() $a\in J$
,
$a\in J$
,
![]() $F\subseteq {{\overline {\Omega }}}$
finite and
$F\subseteq {{\overline {\Omega }}}$
finite and
![]() $p\in {\mathbb {C}}$
with
$p\in {\mathbb {C}}$
with
![]() $n^p=\langle n^p_k:\, k<m \rangle $
and
$n^p=\langle n^p_k:\, k<m \rangle $
and
![]() $c^p= \langle c^p_i :\, i<n^p_{m-1}\rangle $
. We have to show that there is some
$c^p= \langle c^p_i :\, i<n^p_{m-1}\rangle $
. We have to show that there is some
![]() $q\leq p$
and some
$q\leq p$
and some
![]() $k<\omega $
such that q forces
$k<\omega $
such that q forces
that is,
![]() $k\notin a$
and
$k\notin a$
and
![]() $c_k\subseteq c^q_k$
for any
$c_k\subseteq c^q_k$
for any
![]() $\bar c\in F$
. To see this, find some
$\bar c\in F$
. To see this, find some
![]() $n'\in \omega \smallsetminus a$
larger than
$n'\in \omega \smallsetminus a$
larger than
![]() $n^p_{m-1}$
such that, for any
$n^p_{m-1}$
such that, for any
![]() $\bar c\in F$
,
$\bar c\in F$
,
 $$ \begin{align*}\mu\left(\bigcup_{k\geq n'}c_k\right)<\frac{1}{(|F|+1)2^{m+1}}.\end{align*} $$
$$ \begin{align*}\mu\left(\bigcup_{k\geq n'}c_k\right)<\frac{1}{(|F|+1)2^{m+1}}.\end{align*} $$
Define
![]() $q\in {\mathbb {C}}$
such that
$q\in {\mathbb {C}}$
such that
![]() $n^q$
has length
$n^q$
has length
![]() $m+2$
, it extends
$m+2$
, it extends
![]() $n^p$
,
$n^p$
,
![]() $n^q_m:=n'$
and
$n^q_m:=n'$
and
![]() $n^q_{m+1}:=n'+1$
, and such that
$n^q_{m+1}:=n'+1$
, and such that
![]() $c^q$
extends
$c^q$
extends
![]() $c^p$
,
$c^p$
,
![]() $c^q_i=\emptyset $
for all
$c^q_i=\emptyset $
for all
![]() $n^p_{m-1}\leq i< n'$
, and
$n^p_{m-1}\leq i< n'$
, and
![]() $c^q_{n'}:= \bigcup _{\bar c\in F}c_{n'}$
. It is clear that
$c^q_{n'}:= \bigcup _{\bar c\in F}c_{n'}$
. It is clear that
![]() $q\in {\mathbb {C}}$
is stronger than p, and that
$q\in {\mathbb {C}}$
is stronger than p, and that
![]() $c^q_{n'}$
contains
$c^q_{n'}$
contains
![]() $c_{n'}$
for all
$c_{n'}$
for all
![]() $\bar c\in F$
. So
$\bar c\in F$
. So
![]() $k:=n'$
works.
$k:=n'$
works.
Since FS (finite support) iterations of (non-trivial) posets adds Cohen reals at limit steps, we have the following general consequence of the previous lemma.
Theorem 6.2. Let
![]() $\pi $
be a limit ordinal with uncountable cofinality and let
$\pi $
be a limit ordinal with uncountable cofinality and let
![]() ${\mathbb {P}}=\langle {\mathbb {P}}_\alpha ,{\dot {\mathbb {Q}}}_\alpha :\, \alpha <\pi \rangle $
be a FS iteration of non-trivial
${\mathbb {P}}=\langle {\mathbb {P}}_\alpha ,{\dot {\mathbb {Q}}}_\alpha :\, \alpha <\pi \rangle $
be a FS iteration of non-trivial
![]() ${\mathrm {cf}}(\pi )$
-cc posets. Then,
${\mathrm {cf}}(\pi )$
-cc posets. Then,
![]() ${\mathbb {P}}$
forces that there is some (maximal) ideal J such that
${\mathbb {P}}$
forces that there is some (maximal) ideal J such that
![]() ${\mathfrak {b}}_{J}({{\overline {\Omega }}})={\mathrm {add}}({\mathcal {N}}_{J})={\mathrm {add}}({\mathcal {N}}^*_{J})={\mathrm {cof}}({\mathcal {N}}^*_{J})= {\mathrm {cof}}({\mathcal {N}}_{J}) ={\mathfrak {d}}_{J}({{\overline {\Omega }}})={\mathrm {cf}}(\pi )$
.
${\mathfrak {b}}_{J}({{\overline {\Omega }}})={\mathrm {add}}({\mathcal {N}}_{J})={\mathrm {add}}({\mathcal {N}}^*_{J})={\mathrm {cof}}({\mathcal {N}}^*_{J})= {\mathrm {cof}}({\mathcal {N}}_{J}) ={\mathfrak {d}}_{J}({{\overline {\Omega }}})={\mathrm {cf}}(\pi )$
.
Proof Let
![]() $L:=\{0\}\cup {\left \{ {\alpha <\pi } :\, {\alpha \mbox { limit}} \right \}}$
. For each
$L:=\{0\}\cup {\left \{ {\alpha <\pi } :\, {\alpha \mbox { limit}} \right \}}$
. For each
![]() $\alpha \in L$
let
$\alpha \in L$
let
![]() $\bar e_\alpha $
be a
$\bar e_\alpha $
be a
![]() ${\mathbb {P}}_{\alpha +\omega }$
-name of a Cohen real in
${\mathbb {P}}_{\alpha +\omega }$
-name of a Cohen real in
![]() ${{\overline {\Omega }}}$
(in the sense of the proof of Lemma 6.1) over the
${{\overline {\Omega }}}$
(in the sense of the proof of Lemma 6.1) over the
![]() ${\mathbb {P}}_\alpha $
-extension. We construct, by recursion, a sequence
${\mathbb {P}}_\alpha $
-extension. We construct, by recursion, a sequence
![]() $\langle \dot J_\alpha :\, \alpha \in L\cup \{\pi \}\rangle $
such that
$\langle \dot J_\alpha :\, \alpha \in L\cup \{\pi \}\rangle $
such that
![]() $\dot J_\alpha $
is a
$\dot J_\alpha $
is a
![]() ${\mathbb {P}}_\alpha $
-name of an ideal on
${\mathbb {P}}_\alpha $
-name of an ideal on
![]() $\omega $
and
$\omega $
and
![]() ${\mathbb {P}}$
forces that
${\mathbb {P}}$
forces that
![]() $\dot J_\alpha \subseteq \dot J_\beta $
when
$\dot J_\alpha \subseteq \dot J_\beta $
when
![]() $\alpha <\beta $
. We let
$\alpha <\beta $
. We let
![]() $\dot J_0$
be (the
$\dot J_0$
be (the
![]() ${\mathbb {P}}_0$
-name of) any ideal
${\mathbb {P}}_0$
-name of) any ideal
![]() $J_0$
in the ground model.Footnote
7
For the successor step, assume we have constructed
$J_0$
in the ground model.Footnote
7
For the successor step, assume we have constructed
![]() $\dot J_\alpha $
at a stage
$\dot J_\alpha $
at a stage
![]() $\alpha \in L$
. By Lemma 6.1, we obtain a
$\alpha \in L$
. By Lemma 6.1, we obtain a
![]() ${\mathbb {P}}_{\alpha +\omega }$
-name
${\mathbb {P}}_{\alpha +\omega }$
-name
![]() $\dot J_{\alpha +\omega }$
of an ideal extending
$\dot J_{\alpha +\omega }$
of an ideal extending
![]() $\dot J_{\alpha }$
, such that
$\dot J_{\alpha }$
, such that
![]() $\bar e_\alpha \ \subseteq ^{\dot J_{\alpha +\omega }}$
-dominates all the
$\bar e_\alpha \ \subseteq ^{\dot J_{\alpha +\omega }}$
-dominates all the
![]() $\bar c\in {{\overline {\Omega }}}$
from the
$\bar c\in {{\overline {\Omega }}}$
from the
![]() ${\mathbb {P}}_{\alpha }$
-extension. For the limit step, when
${\mathbb {P}}_{\alpha }$
-extension. For the limit step, when
![]() $\gamma $
is a limit point of L (which includes the case
$\gamma $
is a limit point of L (which includes the case
![]() $\gamma =\pi $
), just let
$\gamma =\pi $
), just let
![]() $\dot J_\gamma $
be the
$\dot J_\gamma $
be the
![]() ${\mathbb {P}}_\gamma $
-name of
${\mathbb {P}}_\gamma $
-name of
![]() $\bigcup _{\alpha <\gamma }\dot J_\alpha $
. This finishes the construction.
$\bigcup _{\alpha <\gamma }\dot J_\alpha $
. This finishes the construction.
We show that
![]() $\dot J_\pi $
is as required. In the final generic extension, since
$\dot J_\pi $
is as required. In the final generic extension, since
![]() $\bar e_\alpha \subseteq ^{J_{\beta +\omega }} \bar e_\beta $
for all
$\bar e_\alpha \subseteq ^{J_{\beta +\omega }} \bar e_\beta $
for all
![]() $\alpha <\beta $
in L and
$\alpha <\beta $
in L and
![]() $J_{\beta +\omega }\subseteq J_\pi $
, we obtain
$J_{\beta +\omega }\subseteq J_\pi $
, we obtain
![]() $\bar e_\alpha \subseteq ^{J_\pi } \bar e_\beta $
. To conclude
$\bar e_\alpha \subseteq ^{J_\pi } \bar e_\beta $
. To conclude
![]() ${\mathfrak {b}}_{J_\pi }({{\overline {\Omega }}})={\mathfrak {d}}_{J_\pi }({{\overline {\Omega }}})={\mathrm {cf}}(\pi )$
, it remains to show that
${\mathfrak {b}}_{J_\pi }({{\overline {\Omega }}})={\mathfrak {d}}_{J_\pi }({{\overline {\Omega }}})={\mathrm {cf}}(\pi )$
, it remains to show that
![]() ${\left \{ {\bar e_\alpha } :\, {\alpha \in L} \right \}}$
is
${\left \{ {\bar e_\alpha } :\, {\alpha \in L} \right \}}$
is
![]() $\subseteq ^{J_\pi }$
-dominating (because L is cofinal in
$\subseteq ^{J_\pi }$
-dominating (because L is cofinal in
![]() $\pi $
, and the rest follows by Theorem 5.10). Indeed, if
$\pi $
, and the rest follows by Theorem 5.10). Indeed, if
![]() $\bar c\in {{\overline {\Omega }}}$
in the final extension, then
$\bar c\in {{\overline {\Omega }}}$
in the final extension, then
![]() $\bar c$
is in some intermediate extension at
$\bar c$
is in some intermediate extension at
![]() $\alpha \in L$
, so
$\alpha \in L$
, so
![]() $\bar c \subseteq ^{J_{\alpha +\omega }} \bar e_\alpha $
and hence
$\bar c \subseteq ^{J_{\alpha +\omega }} \bar e_\alpha $
and hence
![]() $\bar c \subseteq ^{J_\pi } \bar e_\alpha $
.
$\bar c \subseteq ^{J_\pi } \bar e_\alpha $
.
It is then clear that
![]() ${\mathfrak {b}}_{J_\pi }({{\overline {\Omega }}})\leq {\mathfrak {d}}_{J_\pi }({{\overline {\Omega }}})\leq {\mathrm {cf}}(\pi )$
. For
${\mathfrak {b}}_{J_\pi }({{\overline {\Omega }}})\leq {\mathfrak {d}}_{J_\pi }({{\overline {\Omega }}})\leq {\mathrm {cf}}(\pi )$
. For
![]() ${\mathrm {cf}}(\pi )\leq {\mathfrak {b}}_{J_\pi }({{\overline {\Omega }}})$
, if
${\mathrm {cf}}(\pi )\leq {\mathfrak {b}}_{J_\pi }({{\overline {\Omega }}})$
, if
![]() $F\subseteq {{\overline {\Omega }}}$
has size
$F\subseteq {{\overline {\Omega }}}$
has size
![]() ${<}{\mathrm {cf}}(\pi )$
, then we can find, for each
${<}{\mathrm {cf}}(\pi )$
, then we can find, for each
![]() $\bar c\in F$
, some
$\bar c\in F$
, some
![]() $\alpha _{\bar c}\in L$
such that
$\alpha _{\bar c}\in L$
such that
![]() $\bar c\subseteq ^{J_\pi } \bar e_{\alpha _{\bar c}}$
. Since
$\bar c\subseteq ^{J_\pi } \bar e_{\alpha _{\bar c}}$
. Since
![]() $|F|<{\mathrm {cf}}(\pi )$
, there is some
$|F|<{\mathrm {cf}}(\pi )$
, there is some
![]() $\beta \in L$
larger than
$\beta \in L$
larger than
![]() $\alpha _{\bar c}$
for all
$\alpha _{\bar c}$
for all
![]() $\bar c\in F$
, so
$\bar c\in F$
, so
![]() $\bar e_{\alpha _{\bar c}}\subseteq ^{J_\pi } \bar e_\beta $
. Then
$\bar e_{\alpha _{\bar c}}\subseteq ^{J_\pi } \bar e_\beta $
. Then
![]() $\bar e_\beta $
is a
$\bar e_\beta $
is a
![]() $\subseteq ^{J_\pi }$
-upper bound of F (because
$\subseteq ^{J_\pi }$
-upper bound of F (because
![]() $\subseteq ^{J_\pi }$
is a transitive relation).
$\subseteq ^{J_\pi }$
is a transitive relation).
Note that any (maximal) ideal extending
![]() $J_\pi $
also satisfies the conclusion (by Theorem 5.11).
$J_\pi $
also satisfies the conclusion (by Theorem 5.11).
The previous results gives a lot of information about the effect of adding many Cohen reals.
Theorem 6.3. Let
![]() $\lambda $
be an uncountable cardinal. Then
$\lambda $
be an uncountable cardinal. Then
![]() ${\mathbb {C}}_\lambda $
forces that, for any regular
${\mathbb {C}}_\lambda $
forces that, for any regular
![]() $\aleph _1\leq \kappa \leq \lambda $
, there is some (maximal) ideal
$\aleph _1\leq \kappa \leq \lambda $
, there is some (maximal) ideal
![]() $J^\kappa $
on
$J^\kappa $
on
![]() $\omega $
such that
$\omega $
such that
![]() ${\mathfrak {b}}_{J^\kappa }({{\overline {\Omega }}})={\mathrm {add}}({\mathcal {N}}_{J^\kappa })={\mathrm {add}}({\mathcal {N}}^*_{J^\kappa })={\mathrm {cof}}({\mathcal {N}}^*_{J^\kappa })= {\mathrm {cof}}({\mathcal {N}}_{J^\kappa }) ={\mathfrak {d}}_{J^\kappa }({{\overline {\Omega }}})=\kappa $
.
${\mathfrak {b}}_{J^\kappa }({{\overline {\Omega }}})={\mathrm {add}}({\mathcal {N}}_{J^\kappa })={\mathrm {add}}({\mathcal {N}}^*_{J^\kappa })={\mathrm {cof}}({\mathcal {N}}^*_{J^\kappa })= {\mathrm {cof}}({\mathcal {N}}_{J^\kappa }) ={\mathfrak {d}}_{J^\kappa }({{\overline {\Omega }}})=\kappa $
.
Proof Let
![]() $\kappa $
be a regular cardinal between
$\kappa $
be a regular cardinal between
![]() $\aleph _1$
and
$\aleph _1$
and
![]() $\lambda $
. Recall that
$\lambda $
. Recall that
![]() ${\mathbb {C}}_\lambda $
is forcing equivalent with
${\mathbb {C}}_\lambda $
is forcing equivalent with
![]() ${\mathbb {C}}_{\lambda +\kappa }$
, so we show that the latter adds the required
${\mathbb {C}}_{\lambda +\kappa }$
, so we show that the latter adds the required
![]() $J^\kappa $
. In fact,
$J^\kappa $
. In fact,
![]() ${\mathbb {C}}_{\lambda +\kappa }$
can be seen as the FS iteration of
${\mathbb {C}}_{\lambda +\kappa }$
can be seen as the FS iteration of
![]() ${\mathbb {C}}$
of length
${\mathbb {C}}$
of length
![]() $\lambda +\kappa $
. Since
$\lambda +\kappa $
. Since
![]() ${\mathrm {cf}}(\lambda +\kappa )=\kappa $
, by Theorem 6.2 we get that
${\mathrm {cf}}(\lambda +\kappa )=\kappa $
, by Theorem 6.2 we get that
![]() ${\mathbb {C}}_{\lambda +\kappa }$
adds the required
${\mathbb {C}}_{\lambda +\kappa }$
adds the required
![]() $J^\kappa $
. Note that any (maximal) ideal extending
$J^\kappa $
. Note that any (maximal) ideal extending
![]() $J^\kappa $
also satisfies the conclusion (by Theorem 5.11).
$J^\kappa $
also satisfies the conclusion (by Theorem 5.11).
Using sums of ideals, we can obtain from the previous theorem that, after adding many Cohen reals, there are non-meager ideals K satisfying
![]() ${\mathrm {non}}({\mathcal {N}}^*_K)<{\mathrm {non}}({\mathcal {N}}_K)$
and
${\mathrm {non}}({\mathcal {N}}^*_K)<{\mathrm {non}}({\mathcal {N}}_K)$
and
![]() ${\mathrm {cov}}({\mathcal {N}}_K)<{\mathrm {cov}}({\mathcal {N}}^*_K)$
(Corollary 6.5). Before proving this, we calculate the cardinal characteristics associated with some operations of ideals.
${\mathrm {cov}}({\mathcal {N}}_K)<{\mathrm {cov}}({\mathcal {N}}^*_K)$
(Corollary 6.5). Before proving this, we calculate the cardinal characteristics associated with some operations of ideals.
Lemma 6.4. Let
![]() ${\mathcal {I}}$
and
${\mathcal {I}}$
and
![]() ${\mathcal {J}}$
be ideals on an infinite set X. Then:
${\mathcal {J}}$
be ideals on an infinite set X. Then:
-
(a)
 $\min \{{\mathrm {add}}({\mathcal {I}}),{\mathrm {add}}({\mathcal {J}})\} \leq {\mathrm {add}}({\mathcal {I}}\cap {\mathcal {J}})$
and
$\min \{{\mathrm {add}}({\mathcal {I}}),{\mathrm {add}}({\mathcal {J}})\} \leq {\mathrm {add}}({\mathcal {I}}\cap {\mathcal {J}})$
and
 ${\mathrm {cof}}({\mathcal {I}}\cap {\mathcal {J}}) \leq \max \{{\mathrm {cof}}({\mathcal {I}}), {\mathrm {cof}}({\mathcal {J}})\}$
.
${\mathrm {cof}}({\mathcal {I}}\cap {\mathcal {J}}) \leq \max \{{\mathrm {cof}}({\mathcal {I}}), {\mathrm {cof}}({\mathcal {J}})\}$
. -
(b)
 ${\mathrm {non}}({\mathcal {I}}\cap {\mathcal {J}})=\min \{{\mathrm {non}}({\mathcal {I}}), {\mathrm {non}}({\mathcal {J}})\}$
and
${\mathrm {non}}({\mathcal {I}}\cap {\mathcal {J}})=\min \{{\mathrm {non}}({\mathcal {I}}), {\mathrm {non}}({\mathcal {J}})\}$
and
 ${\mathrm {cov}}({\mathcal {I}}\cap {\mathcal {J}}) = \max \{{\mathrm {cov}}({\mathcal {I}}), {\mathrm {cov}}({\mathcal {J}})\}$
.
${\mathrm {cov}}({\mathcal {I}}\cap {\mathcal {J}}) = \max \{{\mathrm {cov}}({\mathcal {I}}), {\mathrm {cov}}({\mathcal {J}})\}$
.
For the following items, assume that
![]() ${\mathcal {I}}\cup {\mathcal {J}}$
generates an ideal
${\mathcal {I}}\cup {\mathcal {J}}$
generates an ideal
![]() ${\mathcal {K}}$
.
${\mathcal {K}}$
.
-
(c)
 $\min \{{\mathrm {add}}({\mathcal {I}}),{\mathrm {add}}({\mathcal {J}})\} \leq {\mathrm {add}}({\mathcal {K}})$
and
$\min \{{\mathrm {add}}({\mathcal {I}}),{\mathrm {add}}({\mathcal {J}})\} \leq {\mathrm {add}}({\mathcal {K}})$
and
 ${\mathrm {cof}}({\mathcal {K}}) \leq \max \{{\mathrm {cof}}({\mathcal {I}}),{\mathrm {cof}}({\mathcal {J}})\}$
.
${\mathrm {cof}}({\mathcal {K}}) \leq \max \{{\mathrm {cof}}({\mathcal {I}}),{\mathrm {cof}}({\mathcal {J}})\}$
. -
(d)
 $\max \{{\mathrm {non}}({\mathcal {I}}),{\mathrm {non}}({\mathcal {J}})\} \leq {\mathrm {non}}({\mathcal {K}})$
and
$\max \{{\mathrm {non}}({\mathcal {I}}),{\mathrm {non}}({\mathcal {J}})\} \leq {\mathrm {non}}({\mathcal {K}})$
and
 ${\mathrm {cov}}({\mathcal {K}}) \leq \min \{{\mathrm {cov}}({\mathcal {I}}),{\mathrm {cov}}({\mathcal {J}})\}$
.
${\mathrm {cov}}({\mathcal {K}}) \leq \min \{{\mathrm {cov}}({\mathcal {I}}),{\mathrm {cov}}({\mathcal {J}})\}$
.
Proof We use the product of relational systems to shorten this proof. If
![]() ${\mathbf {R}}=\langle X,Y,R\rangle $
and
${\mathbf {R}}=\langle X,Y,R\rangle $
and
![]() ${\mathbf {R}}'=\langle X',Y',R'\rangle $
are relational systems, we define
${\mathbf {R}}'=\langle X',Y',R'\rangle $
are relational systems, we define
![]() ${\mathbf {R}}\times {\mathbf {R}}':=\langle X\times X', Y\times Y', R^\times \rangle $
with the relation
${\mathbf {R}}\times {\mathbf {R}}':=\langle X\times X', Y\times Y', R^\times \rangle $
with the relation
![]() $(x,x')\, R^\times \, (y,y')$
iff
$(x,x')\, R^\times \, (y,y')$
iff
![]() $x\, R\, y$
and
$x\, R\, y$
and
![]() $x'\, R'\, y'$
. Recall that
$x'\, R'\, y'$
. Recall that
![]() ${\mathfrak {b}}({\mathbf {R}}\times {\mathbf {R}}')=\min \{{\mathfrak {b}}({\mathbf {R}}),{\mathfrak {b}}({\mathbf {R}}')\}$
and
${\mathfrak {b}}({\mathbf {R}}\times {\mathbf {R}}')=\min \{{\mathfrak {b}}({\mathbf {R}}),{\mathfrak {b}}({\mathbf {R}}')\}$
and
![]() $\max \{{\mathfrak {d}}({\mathbf {R}}),{\mathfrak {d}}({\mathbf {R}}')\}\leq {\mathfrak {d}}({\mathbf {R}}\times {\mathbf {R}}')\leq {\mathfrak {d}}({\mathbf {R}})\cdot {\mathfrak {d}}({\mathbf {R}}')$
(so equality holds when some
$\max \{{\mathfrak {d}}({\mathbf {R}}),{\mathfrak {d}}({\mathbf {R}}')\}\leq {\mathfrak {d}}({\mathbf {R}}\times {\mathbf {R}}')\leq {\mathfrak {d}}({\mathbf {R}})\cdot {\mathfrak {d}}({\mathbf {R}}')$
(so equality holds when some
![]() ${\mathfrak {d}}$
-number is infinite), see, e.g., [Reference Blass9, Section 4].
${\mathfrak {d}}$
-number is infinite), see, e.g., [Reference Blass9, Section 4].
As relational systems, it is easy to show that
![]() ${\mathcal {I}}\cap {\mathcal {J}} {\mathrel {\preceq _{\mathrm {T}}}} {\mathcal {I}}\times {\mathcal {J}}$
and
${\mathcal {I}}\cap {\mathcal {J}} {\mathrel {\preceq _{\mathrm {T}}}} {\mathcal {I}}\times {\mathcal {J}}$
and
![]() ${\mathbf {C}}_{{\mathcal {I}}\cap {\mathcal {J}}}{\mathrel {\preceq _{\mathrm {T}}}} {\mathbf {C}}_{\mathcal {I}}\times {\mathbf {C}}_{\mathcal {J}}$
, which implies (a),
${\mathbf {C}}_{{\mathcal {I}}\cap {\mathcal {J}}}{\mathrel {\preceq _{\mathrm {T}}}} {\mathbf {C}}_{\mathcal {I}}\times {\mathbf {C}}_{\mathcal {J}}$
, which implies (a),
![]() $\min \{{\mathrm {non}}({\mathcal {I}}), {\mathrm {non}}({\mathcal {J}})\}\leq {\mathrm {non}}({\mathcal {I}}\cap {\mathcal {J}})$
and
$\min \{{\mathrm {non}}({\mathcal {I}}), {\mathrm {non}}({\mathcal {J}})\}\leq {\mathrm {non}}({\mathcal {I}}\cap {\mathcal {J}})$
and
![]() ${\mathrm {cov}}({\mathcal {I}}\cap {\mathcal {J}}) \leq \max \{{\mathrm {cov}}({\mathcal {I}}),{\mathrm {cov}}({\mathcal {J}})\}$
. The converse inequality for the uniformity and the covering follows by Corollary 5.3, as well as (d).
${\mathrm {cov}}({\mathcal {I}}\cap {\mathcal {J}}) \leq \max \{{\mathrm {cov}}({\mathcal {I}}),{\mathrm {cov}}({\mathcal {J}})\}$
. The converse inequality for the uniformity and the covering follows by Corollary 5.3, as well as (d).
We can also show that
![]() ${\mathcal {K}}{\mathrel {\preceq _{\mathrm {T}}}} {\mathcal {I}}\times {\mathcal {J}}$
, which implies (c).
${\mathcal {K}}{\mathrel {\preceq _{\mathrm {T}}}} {\mathcal {I}}\times {\mathcal {J}}$
, which implies (c).
Corollary 6.5 (of Theorem 6.3).
The poset
![]() ${\mathbb {C}}_\lambda $
forces that, for any regular
${\mathbb {C}}_\lambda $
forces that, for any regular
![]() ${{\aleph _1\leq \kappa _1\leq \kappa _2\leq \lambda }}$
, there is some non-meager ideal K such that
${{\aleph _1\leq \kappa _1\leq \kappa _2\leq \lambda }}$
, there is some non-meager ideal K such that
 $$ \begin{align*} {\mathrm{add}}({\mathcal{N}}^*_K)= {\mathrm{add}}({\mathcal{N}}_K) = {\mathrm{non}}({\mathcal{N}}^*_K) = {\mathrm{cov}}({\mathcal{N}}_K) & = \kappa_1,\\ {\mathrm{cof}}({\mathcal{N}}^*_K)= {\mathrm{cof}}({\mathcal{N}}_K) = {\mathrm{cov}}({\mathcal{N}}^*_K) = {\mathrm{non}}({\mathcal{N}}_K) & = \kappa_2. \end{align*} $$
$$ \begin{align*} {\mathrm{add}}({\mathcal{N}}^*_K)= {\mathrm{add}}({\mathcal{N}}_K) = {\mathrm{non}}({\mathcal{N}}^*_K) = {\mathrm{cov}}({\mathcal{N}}_K) & = \kappa_1,\\ {\mathrm{cof}}({\mathcal{N}}^*_K)= {\mathrm{cof}}({\mathcal{N}}_K) = {\mathrm{cov}}({\mathcal{N}}^*_K) = {\mathrm{non}}({\mathcal{N}}_K) & = \kappa_2. \end{align*} $$
Proof In the
![]() ${\mathbb {C}}_\lambda $
-generic extension, let
${\mathbb {C}}_\lambda $
-generic extension, let
![]() $J^\kappa $
be a maximal ideal as in Theorem 6.3. We show that
$J^\kappa $
be a maximal ideal as in Theorem 6.3. We show that
![]() $K:= J^{\kappa _1}\oplus J^{\kappa _2}$
is the required ideal. By Example 2.13,
$K:= J^{\kappa _1}\oplus J^{\kappa _2}$
is the required ideal. By Example 2.13,
![]() ${{\mathcal {N}}^*_K={\mathcal {N}}^*_{J^{\kappa _1}}\cap {\mathcal {N}}^*_{J^{\kappa _2}}}$
and
${{\mathcal {N}}^*_K={\mathcal {N}}^*_{J^{\kappa _1}}\cap {\mathcal {N}}^*_{J^{\kappa _2}}}$
and
![]() ${\mathcal {N}}_K$
is the ideal generated by
${\mathcal {N}}_K$
is the ideal generated by
![]() ${\mathcal {N}}^*_{J^{\kappa _1}}\cup {\mathcal {N}}^*_{J^{\kappa _2}}$
, so by Lemma 6.4 we can perform the following calculations:
${\mathcal {N}}^*_{J^{\kappa _1}}\cup {\mathcal {N}}^*_{J^{\kappa _2}}$
, so by Lemma 6.4 we can perform the following calculations:
 $$ \begin{align*} \kappa_1 & =\min\{{\mathrm{add}}({\mathcal{N}}^*_{J^{\kappa_1}}),{\mathrm{add}}({\mathcal{N}}^*_{J^{\kappa_2}})\} \leq {\mathrm{add}}({\mathcal{N}}^*_K)\\ & \leq {\mathrm{non}}({\mathcal{N}}^*_K)=\min\{{\mathrm{non}}({\mathcal{N}}^*_{J^{\kappa_1}}),{\mathrm{non}}({\mathcal{N}}^*_{J^{\kappa_2}})\}=\kappa_1;\\ \kappa_1 & =\min\{{\mathrm{add}}({\mathcal{N}}_{J^{\kappa_1}}),{\mathrm{add}}({\mathcal{N}}_{J^{\kappa_2}})\} \leq {\mathrm{add}}({\mathcal{N}}_K)\\ &\leq {\mathrm{cov}}({\mathcal{N}}_K) \leq \min\{{\mathrm{cov}}({\mathcal{N}}_{J^{\kappa_1}}),{\mathrm{cov}}({\mathcal{N}}_{J^{\kappa_2}})\}=\kappa_1;\\ \kappa_2 & =\max\{{\mathrm{cov}}({\mathcal{N}}^*_{J^{\kappa_1}}),{\mathrm{cov}}({\mathcal{N}}^*_{J^{\kappa_2}})\} = {\mathrm{cov}}({\mathcal{N}}^*_K)\\ & \leq {\mathrm{cof}}({\mathcal{N}}^*_K) \leq \max\{{\mathrm{cof}}({\mathcal{N}}^*_{J^{\kappa_1}}),{\mathrm{cof}}({\mathcal{N}}^*_{J^{\kappa_2}})\}=\kappa_2;\\ \kappa_2 & =\max\{{\mathrm{non}}({\mathcal{N}}_{J^{\kappa_1}}),{\mathrm{non}}({\mathcal{N}}_{J^{\kappa_2}})\} \leq {\mathrm{non}}({\mathcal{N}}_K)\\ & \leq {\mathrm{cof}}({\mathcal{N}}_K) \leq \max\{{\mathrm{cof}}({\mathcal{N}}_{J^{\kappa_1}}),{\mathrm{cof}}({\mathcal{N}}_{J^{\kappa_2}})\}=\kappa_2.\\[-35pt]\end{align*} $$
$$ \begin{align*} \kappa_1 & =\min\{{\mathrm{add}}({\mathcal{N}}^*_{J^{\kappa_1}}),{\mathrm{add}}({\mathcal{N}}^*_{J^{\kappa_2}})\} \leq {\mathrm{add}}({\mathcal{N}}^*_K)\\ & \leq {\mathrm{non}}({\mathcal{N}}^*_K)=\min\{{\mathrm{non}}({\mathcal{N}}^*_{J^{\kappa_1}}),{\mathrm{non}}({\mathcal{N}}^*_{J^{\kappa_2}})\}=\kappa_1;\\ \kappa_1 & =\min\{{\mathrm{add}}({\mathcal{N}}_{J^{\kappa_1}}),{\mathrm{add}}({\mathcal{N}}_{J^{\kappa_2}})\} \leq {\mathrm{add}}({\mathcal{N}}_K)\\ &\leq {\mathrm{cov}}({\mathcal{N}}_K) \leq \min\{{\mathrm{cov}}({\mathcal{N}}_{J^{\kappa_1}}),{\mathrm{cov}}({\mathcal{N}}_{J^{\kappa_2}})\}=\kappa_1;\\ \kappa_2 & =\max\{{\mathrm{cov}}({\mathcal{N}}^*_{J^{\kappa_1}}),{\mathrm{cov}}({\mathcal{N}}^*_{J^{\kappa_2}})\} = {\mathrm{cov}}({\mathcal{N}}^*_K)\\ & \leq {\mathrm{cof}}({\mathcal{N}}^*_K) \leq \max\{{\mathrm{cof}}({\mathcal{N}}^*_{J^{\kappa_1}}),{\mathrm{cof}}({\mathcal{N}}^*_{J^{\kappa_2}})\}=\kappa_2;\\ \kappa_2 & =\max\{{\mathrm{non}}({\mathcal{N}}_{J^{\kappa_1}}),{\mathrm{non}}({\mathcal{N}}_{J^{\kappa_2}})\} \leq {\mathrm{non}}({\mathcal{N}}_K)\\ & \leq {\mathrm{cof}}({\mathcal{N}}_K) \leq \max\{{\mathrm{cof}}({\mathcal{N}}_{J^{\kappa_1}}),{\mathrm{cof}}({\mathcal{N}}_{J^{\kappa_2}})\}=\kappa_2.\\[-35pt]\end{align*} $$
We do not know how to force that there is some non-meager ideal K such that
![]() ${\mathrm {add}}({\mathcal {N}}^*_K)\neq {\mathrm {add}}({\mathcal {N}}_K)$
, likewise for the cofinality.
${\mathrm {add}}({\mathcal {N}}^*_K)\neq {\mathrm {add}}({\mathcal {N}}_K)$
, likewise for the cofinality.
Using Theorem 6.3 and well-known forcing models, we can show that ZFC cannot prove more inequalities of the cardinal characteristics associated with our new ideals with the classical cardinal characteristics of the continuum of Figure 6, but leaving some few open questions. We skip most of the details in the following items, but the reader can refer to the definition of the cardinal characteristics and their inequalities in [Reference Balcar, Hernández-Hernández and Hrušák1, Reference Bartoszyński and Judah4, Reference Blass9], and learn the forcing techniques from, e.g., [Reference Bartoszyński and Judah4, Reference Blass9, Reference Brendle14, Reference Mejía32, Reference Mejía33].

Figure 6 Cichoń’s diagram and the Blass diagram combined, also including the coverings and uniformities of our new ideals. An arrow
![]() $\mathfrak x\rightarrow \mathfrak y$
means that ZFC proves
$\mathfrak x\rightarrow \mathfrak y$
means that ZFC proves
![]() $\mathfrak x\le \mathfrak y$
.
$\mathfrak x\le \mathfrak y$
.
-
(M1) Using
 $\lambda>\aleph _2$
,
$\lambda>\aleph _2$
,
 ${\mathbb {C}}_\lambda $
forces that there is some (maximal) ideal J on
${\mathbb {C}}_\lambda $
forces that there is some (maximal) ideal J on
 $\omega $
such that
$\omega $
such that
 ${\mathrm {non}}({\mathcal {M}})={\mathfrak {g}} ={\mathfrak {a}}=\aleph _1< {\mathrm {add}}({\mathcal {N}}_J)={\mathrm {cof}}({\mathcal {N}}_J) ={\mathrm {add}}({\mathcal {N}}^*_J) ={\mathrm {cof}}({\mathcal {N}}^*_J)<{\mathrm {cov}}({\mathcal {M}})$
(see Theorem 6.3).
${\mathrm {non}}({\mathcal {M}})={\mathfrak {g}} ={\mathfrak {a}}=\aleph _1< {\mathrm {add}}({\mathcal {N}}_J)={\mathrm {cof}}({\mathcal {N}}_J) ={\mathrm {add}}({\mathcal {N}}^*_J) ={\mathrm {cof}}({\mathcal {N}}^*_J)<{\mathrm {cov}}({\mathcal {M}})$
(see Theorem 6.3). -
(M2) We can iterate the Hechler poset, followed by a large random algebra, to force
 ${\mathrm {non}}({\mathcal {N}})=\aleph _1<{\mathfrak {b}}={\mathfrak {d}}={\mathfrak {a}}<{\mathrm {cov}}({\mathcal {N}})={\mathfrak {c}}$
. In this generic extension, we obtain
${\mathrm {non}}({\mathcal {N}})=\aleph _1<{\mathfrak {b}}={\mathfrak {d}}={\mathfrak {a}}<{\mathrm {cov}}({\mathcal {N}})={\mathfrak {c}}$
. In this generic extension, we obtain
 ${\mathrm {add}}({\mathcal {N}}_J)= {\mathrm {add}}({\mathcal {N}}^*_J) = {\mathrm {non}}({\mathcal {N}}_J)= {\mathrm {non}}({\mathcal {N}}^*_J)={\mathfrak {g}} =\aleph _1<{\mathfrak {b}}={\mathfrak {d}}={\mathfrak {a}}<{\mathrm {cov}}({\mathcal {N}}_J)= {\mathrm {cov}}({\mathcal {N}}^*_J) = {\mathrm {cof}}({\mathcal {N}}_J)= {\mathrm {cof}}({\mathcal {N}}^*_J)={\mathfrak {c}}$
for any ideal J on
${\mathrm {add}}({\mathcal {N}}_J)= {\mathrm {add}}({\mathcal {N}}^*_J) = {\mathrm {non}}({\mathcal {N}}_J)= {\mathrm {non}}({\mathcal {N}}^*_J)={\mathfrak {g}} =\aleph _1<{\mathfrak {b}}={\mathfrak {d}}={\mathfrak {a}}<{\mathrm {cov}}({\mathcal {N}}_J)= {\mathrm {cov}}({\mathcal {N}}^*_J) = {\mathrm {cof}}({\mathcal {N}}_J)= {\mathrm {cof}}({\mathcal {N}}^*_J)={\mathfrak {c}}$
for any ideal J on
 $\omega $
. This idea to force with a random algebra after some other FS iteration of ccc posets is original from Brendle, but some details can be found in [Reference Goldstern, Kellner, Mejía and Shelah22, Section 5].
$\omega $
. This idea to force with a random algebra after some other FS iteration of ccc posets is original from Brendle, but some details can be found in [Reference Goldstern, Kellner, Mejía and Shelah22, Section 5]. -
(M3) In the Miller model,
 ${\mathrm {non}}({\mathcal {M}})={\mathrm {non}}({\mathcal {N}})={\mathfrak {u}}={\mathfrak {a}}=\aleph _1<{\mathfrak {g}}={\mathfrak {c}}=\aleph _2$
, so NCF follows. Hence
${\mathrm {non}}({\mathcal {M}})={\mathrm {non}}({\mathcal {N}})={\mathfrak {u}}={\mathfrak {a}}=\aleph _1<{\mathfrak {g}}={\mathfrak {c}}=\aleph _2$
, so NCF follows. Hence
 ${\mathrm {add}}({\mathcal {N}}_J)= {\mathrm {add}}({\mathcal {N}}^*_J) = {\mathrm {non}}({\mathcal {N}}_J)= {\mathrm {non}}({\mathcal {N}}^*_J)= {\mathrm {cov}}({\mathcal {N}}_J) = {\mathrm {cov}}({\mathcal {N}}^*_J)=\aleph _1 < {\mathfrak {g}}={\mathfrak {c}}=\aleph _2$
for any ideal J on
${\mathrm {add}}({\mathcal {N}}_J)= {\mathrm {add}}({\mathcal {N}}^*_J) = {\mathrm {non}}({\mathcal {N}}_J)= {\mathrm {non}}({\mathcal {N}}^*_J)= {\mathrm {cov}}({\mathcal {N}}_J) = {\mathrm {cov}}({\mathcal {N}}^*_J)=\aleph _1 < {\mathfrak {g}}={\mathfrak {c}}=\aleph _2$
for any ideal J on
 $\omega $
, e.g., since ZFC proves
$\omega $
, e.g., since ZFC proves
 ${\mathrm {cov}}({\mathcal {E}})\leq {\mathfrak {r}}\leq {\mathfrak {u}}$
,
${\mathrm {cov}}({\mathcal {E}})\leq {\mathfrak {r}}\leq {\mathfrak {u}}$
,
 ${\mathrm {cov}}({\mathcal {E}})=\aleph _1$
in the Miller model. Although
${\mathrm {cov}}({\mathcal {E}})=\aleph _1$
in the Miller model. Although
 ${\mathrm {cof}}({\mathcal {N}}_J)$
and
${\mathrm {cof}}({\mathcal {N}}_J)$
and
 ${\mathrm {cof}}({\mathcal {N}}^*_J)$
are
${\mathrm {cof}}({\mathcal {N}}^*_J)$
are
 $\aleph _2$
when J has the Baire property, we do not know what happens when J does not have the Baire property (or just in the case of maximal ideals).
$\aleph _2$
when J has the Baire property, we do not know what happens when J does not have the Baire property (or just in the case of maximal ideals). -
(M4) In the Mathias model,
 ${\mathrm {cov}}({\mathcal {E}})=\aleph _1<{\mathfrak {h}}={\mathfrak {c}}=\aleph _2$
(the first equality due to the Laver property). Hence
${\mathrm {cov}}({\mathcal {E}})=\aleph _1<{\mathfrak {h}}={\mathfrak {c}}=\aleph _2$
(the first equality due to the Laver property). Hence
 ${\mathrm {add}}({\mathcal {N}}_J)= {\mathrm {add}}({\mathcal {N}}^*_J)= {\mathrm {cov}}({\mathcal {N}}_J) = {\mathrm {cov}}({\mathcal {N}}^*_J)=\aleph _1 < {\mathrm {non}}({\mathcal {N}}_J)= {\mathrm {non}}({\mathcal {N}}^*_J)= {\mathrm {cof}}({\mathcal {N}}_J) = {\mathrm {cof}}({\mathcal {N}}^*_J)= \aleph _2$
(notice that
${\mathrm {add}}({\mathcal {N}}_J)= {\mathrm {add}}({\mathcal {N}}^*_J)= {\mathrm {cov}}({\mathcal {N}}_J) = {\mathrm {cov}}({\mathcal {N}}^*_J)=\aleph _1 < {\mathrm {non}}({\mathcal {N}}_J)= {\mathrm {non}}({\mathcal {N}}^*_J)= {\mathrm {cof}}({\mathcal {N}}_J) = {\mathrm {cof}}({\mathcal {N}}^*_J)= \aleph _2$
(notice that
 ${\mathfrak {h}}\leq {\mathfrak {s}}\leq {\mathrm {non}}({\mathcal {E}})$
).
${\mathfrak {h}}\leq {\mathfrak {s}}\leq {\mathrm {non}}({\mathcal {E}})$
). -
(M5) Assume
 $\kappa $
and
$\kappa $
and
 $\lambda $
cardinals such that
$\lambda $
cardinals such that
 $\aleph _1\leq \kappa \leq \lambda =\lambda ^{\aleph _0}$
. The FS iteration of Hechler forcing of length
$\aleph _1\leq \kappa \leq \lambda =\lambda ^{\aleph _0}$
. The FS iteration of Hechler forcing of length
 $\lambda \kappa $
(ordinal product) forces
$\lambda \kappa $
(ordinal product) forces
 ${\mathfrak {e}}= {\mathfrak {g}}={\mathfrak {s}} =\aleph _1$
,
${\mathfrak {e}}= {\mathfrak {g}}={\mathfrak {s}} =\aleph _1$
,
 ${\mathrm {add}}({\mathcal {M}})={\mathrm {cof}}({\mathcal {M}})=\kappa $
and
${\mathrm {add}}({\mathcal {M}})={\mathrm {cof}}({\mathcal {M}})=\kappa $
and
 ${\mathrm {non}}({\mathcal {N}})={\mathfrak {r}}={\mathfrak {c}}=\lambda $
. Thanks to Theorem 6.2, there is a (maximal) ideal
${\mathrm {non}}({\mathcal {N}})={\mathfrak {r}}={\mathfrak {c}}=\lambda $
. Thanks to Theorem 6.2, there is a (maximal) ideal
 $J^\kappa $
on
$J^\kappa $
on
 $\omega $
such that
$\omega $
such that
 ${\mathrm {add}}({\mathcal {N}}_{J^\kappa })={\mathrm {add}}({\mathcal {N}}^*_{J^\kappa })={\mathrm {cof}}({\mathcal {N}}^*_{J^\kappa })= {\mathrm {cof}}({\mathcal {N}}_{J^\kappa })=\kappa $
. In general, we can just say that the additivities and coverings of
${\mathrm {add}}({\mathcal {N}}_{J^\kappa })={\mathrm {add}}({\mathcal {N}}^*_{J^\kappa })={\mathrm {cof}}({\mathcal {N}}^*_{J^\kappa })= {\mathrm {cof}}({\mathcal {N}}_{J^\kappa })=\kappa $
. In general, we can just say that the additivities and coverings of
 ${\mathcal {N}}_J$
and
${\mathcal {N}}_J$
and
 ${\mathcal {N}}^*_J$
are below
${\mathcal {N}}^*_J$
are below
 $\kappa $
, and that their uniformities and cofinalities are above
$\kappa $
, and that their uniformities and cofinalities are above
 $\kappa $
for any ideal J on
$\kappa $
for any ideal J on
 $\omega $
.
$\omega $
.Since the Hechler poset makes the set of reals from the ground model meager, we have that any ideal
 $J_0$
on
$J_0$
on
 $\omega $
with a set of generators in the ground model (or in any intermediate extension) is meager in the final extension, so
$\omega $
with a set of generators in the ground model (or in any intermediate extension) is meager in the final extension, so
 ${\mathrm {cov}}({\mathcal {N}}_{J_0})=\aleph _1$
and
${\mathrm {cov}}({\mathcal {N}}_{J_0})=\aleph _1$
and
 ${\mathrm {non}}({\mathcal {N}}_{J_0})={\mathfrak {c}}=\lambda $
. We still do not know how to obtain a maximal (or just non-meager) ideal
${\mathrm {non}}({\mathcal {N}}_{J_0})={\mathfrak {c}}=\lambda $
. We still do not know how to obtain a maximal (or just non-meager) ideal
 $J'$
in the final extension such that
$J'$
in the final extension such that
 ${\mathrm {cov}}({\mathcal {N}}_{J'})=\aleph _1$
and
${\mathrm {cov}}({\mathcal {N}}_{J'})=\aleph _1$
and
 ${\mathrm {non}}({\mathcal {N}}_{J'})=\lambda $
.
${\mathrm {non}}({\mathcal {N}}_{J'})=\lambda $
. -
(M6) With
 $\kappa $
and
$\kappa $
and
 $\lambda $
as in (M5), there is a FS iteration of length
$\lambda $
as in (M5), there is a FS iteration of length
 $\lambda \kappa $
of
$\lambda \kappa $
of
 $\sigma $
-centered posets forcing
$\sigma $
-centered posets forcing
 ${\mathrm {cov}}({\mathcal {N}})=\aleph _1$
,
${\mathrm {cov}}({\mathcal {N}})=\aleph _1$
,
 ${\mathfrak {p}}={\mathfrak {u}}={\mathfrak {a}}={\mathfrak {i}}=\kappa $
and
${\mathfrak {p}}={\mathfrak {u}}={\mathfrak {a}}={\mathfrak {i}}=\kappa $
and
 ${\mathrm {non}}({\mathcal {N}})={\mathfrak {c}}=\lambda $
. For example, by counting arguments, we make sure to force with all
${\mathrm {non}}({\mathcal {N}})={\mathfrak {c}}=\lambda $
. For example, by counting arguments, we make sure to force with all
 $\sigma $
-centered posets of size
$\sigma $
-centered posets of size
 ${<}\kappa $
, while adding witnesses of
${<}\kappa $
, while adding witnesses of
 ${\mathfrak {u}}$
,
${\mathfrak {u}}$
,
 ${\mathfrak {a}}$
and
${\mathfrak {a}}$
and
 ${\mathfrak {i}}$
of size
${\mathfrak {i}}$
of size
 $\kappa $
using a cofinal subset of
$\kappa $
using a cofinal subset of
 $\lambda \kappa $
of size
$\lambda \kappa $
of size
 $\kappa $
(for
$\kappa $
(for
 ${\mathfrak {u}}$
, use Mathias–Prikry forcing with ultrafilters, and for
${\mathfrak {u}}$
, use Mathias–Prikry forcing with ultrafilters, and for
 ${\mathfrak {a}}$
and
${\mathfrak {a}}$
and
 ${\mathfrak {i}}$
use Hechler-type posets as in [Reference Hechler24], all of which are
${\mathfrak {i}}$
use Hechler-type posets as in [Reference Hechler24], all of which are
 $\sigma $
-centered). We have exactly the same situation of the previous model for the cardinal characteristics associated with
$\sigma $
-centered). We have exactly the same situation of the previous model for the cardinal characteristics associated with
 ${\mathcal {N}}_J$
and
${\mathcal {N}}_J$
and
 ${\mathcal {N}}^*_J$
.
${\mathcal {N}}^*_J$
. -
(M7) Over a model of CH, the countable support iteration of length
 $\omega _2$
of the tree forcing from [Reference Brendle15, Lemma 2] forces
$\omega _2$
of the tree forcing from [Reference Brendle15, Lemma 2] forces
 ${\mathfrak {d}}= {\mathrm {cov}}({\mathcal {E}})=\aleph _1<{\mathrm {non}}({\mathcal {E}})=\aleph _2$
. Concretely, this forcing is proper,
${\mathfrak {d}}= {\mathrm {cov}}({\mathcal {E}})=\aleph _1<{\mathrm {non}}({\mathcal {E}})=\aleph _2$
. Concretely, this forcing is proper,
 ${{}^\omega \omega }$
-bounding, and does not add random reals (see also [Reference Bartoszyński and Judah4, Section 7.3B]), hence
${{}^\omega \omega }$
-bounding, and does not add random reals (see also [Reference Bartoszyński and Judah4, Section 7.3B]), hence
 ${\mathrm {cov}}({\mathcal {E}})\leq \max \{{\mathfrak {d}},{\mathrm {cov}}({\mathcal {N}})\}=\aleph _1$
(see Theorem 5.4). In this generic extension, all additivities and coverings of
${\mathrm {cov}}({\mathcal {E}})\leq \max \{{\mathfrak {d}},{\mathrm {cov}}({\mathcal {N}})\}=\aleph _1$
(see Theorem 5.4). In this generic extension, all additivities and coverings of
 ${\mathcal {N}}_J$
and
${\mathcal {N}}_J$
and
 ${\mathcal {N}}^*_J$
are
${\mathcal {N}}^*_J$
are
 $\aleph _1$
, while the uniformities and cofinalities are
$\aleph _1$
, while the uniformities and cofinalities are
 $\aleph _2$
.
$\aleph _2$
. -
(M8) Brendle’s model [Reference Brendle16] of
 ${\mathrm {cof}}({\mathcal {N}})<{\mathfrak {a}}$
clearly satisfies that the cardinal characteristics associated with
${\mathrm {cof}}({\mathcal {N}})<{\mathfrak {a}}$
clearly satisfies that the cardinal characteristics associated with
 ${\mathcal {N}}_J$
and
${\mathcal {N}}_J$
and
 ${\mathcal {N}}^*_J$
are strictly smaller than
${\mathcal {N}}^*_J$
are strictly smaller than
 ${\mathfrak {a}}$
for every ideal J on
${\mathfrak {a}}$
for every ideal J on
 $\omega $
.
$\omega $
.
It is not clear from the above whether
![]() ${\mathfrak {g}} \leq {\mathrm {cof}}({\mathcal {N}}_J)$
in ZFC for all J, and whether we can force
${\mathfrak {g}} \leq {\mathrm {cof}}({\mathcal {N}}_J)$
in ZFC for all J, and whether we can force
![]() ${\mathrm {cov}}({\mathcal {N}}_J)<{\mathfrak {p}}$
and
${\mathrm {cov}}({\mathcal {N}}_J)<{\mathfrak {p}}$
and
![]() ${\mathrm {non}}({\mathcal {N}}_J)>\max \{{\mathfrak {u}},{\mathfrak {i}}\}$
for some non-meager J.
${\mathrm {non}}({\mathcal {N}}_J)>\max \{{\mathfrak {u}},{\mathfrak {i}}\}$
for some non-meager J.
7 Discussions and open questions
We developed our work in the Cantor space, but we could as well work in other Polish spaces with a measure (on the Borel
![]() $\sigma $
-algebra), like
$\sigma $
-algebra), like
![]() ${\mathbb {R}}$
, the unit interval, and any product
${\mathbb {R}}$
, the unit interval, and any product
![]() $\prod _{n<\omega } b(n)$
of discrete finite spaces such that
$\prod _{n<\omega } b(n)$
of discrete finite spaces such that
![]() $|b(n)|\geq 2$
for infinitely many n (note that the Cantor space is a particular case). In the case of
$|b(n)|\geq 2$
for infinitely many n (note that the Cantor space is a particular case). In the case of
![]() ${\mathbb {R}}$
, for a fixed countable base B, we can replace
${\mathbb {R}}$
, for a fixed countable base B, we can replace
![]() $\Omega $
by the collection of open sets that can be written as a finite union of sets from B. For
$\Omega $
by the collection of open sets that can be written as a finite union of sets from B. For
![]() $\prod _{n<\omega } b(n)$
, we can look at clopen subsets and the product measure of the uniform measures. We can define
$\prod _{n<\omega } b(n)$
, we can look at clopen subsets and the product measure of the uniform measures. We can define
![]() ${\mathcal {N}}_J$
and
${\mathcal {N}}_J$
and
![]() ${\mathcal {N}}^*_J$
for these spaces, and prove the same results similarly. Alternatively, we can use the natural “almost homeomorphisms” between
${\mathcal {N}}^*_J$
for these spaces, and prove the same results similarly. Alternatively, we can use the natural “almost homeomorphisms” between
![]() $\prod _{n<\omega } b(n)$
and the unit interval to transfer results from one space to the other. For example, the cardinal characteristics associated with
$\prod _{n<\omega } b(n)$
and the unit interval to transfer results from one space to the other. For example, the cardinal characteristics associated with
![]() ${\mathcal {N}}_J$
and
${\mathcal {N}}_J$
and
![]() ${\mathcal {N}}^*_J$
are the same because the relational systems for
${\mathcal {N}}^*_J$
are the same because the relational systems for
![]() ${\mathcal {N}}_J$
are Tukey equivalent for two different spaces, and the same applies to
${\mathcal {N}}_J$
are Tukey equivalent for two different spaces, and the same applies to
![]() ${\mathbf {C}}_{{\mathcal {N}}_J}$
,
${\mathbf {C}}_{{\mathcal {N}}_J}$
,
![]() ${\mathcal {N}}^*_J$
and
${\mathcal {N}}^*_J$
and
![]() ${\mathbf {C}}_{{\mathcal {N}}^*_J}$
.
${\mathbf {C}}_{{\mathcal {N}}^*_J}$
.
In a preliminary version of this work [Reference Šottová40], we considered a weaker notion of
![]() ${\mathcal {N}}_J$
and
${\mathcal {N}}_J$
and
![]() ${\mathcal {N}}^*_J$
by using, instead of
${\mathcal {N}}^*_J$
by using, instead of
![]() ${{\overline {\Omega }}}$
,
${{\overline {\Omega }}}$
,
 $$ \begin{align*}{{\ell^1({\Omega})}}:={\left\{ {\bar c\in {}^\omega \Omega} :\, {\sum_{n<\omega}\mu(c_n) < \infty} \right\}}.\end{align*} $$
$$ \begin{align*}{{\ell^1({\Omega})}}:={\left\{ {\bar c\in {}^\omega \Omega} :\, {\sum_{n<\omega}\mu(c_n) < \infty} \right\}}.\end{align*} $$
Although we do not know whether we have the same ideals in this way, many results of this paper can be repeated for this weaker notion.
More details about the discussion in the previous paragraphs can be found in the arXiv version of this paper.Footnote 8
We now address several open questions of this work.
Question 7.1. Does some converse of the statements in Theorem 2.15 hold in ZFC?
Concerning nearly coherence, we ask the following.
Question 7.2. Does NCF imply that there is only one
![]() ${\mathcal {N}}_J$
for non-meager J?
${\mathcal {N}}_J$
for non-meager J?
We may also ask whether (under NCF)
![]() ${\mathcal {N}}^*_J={\mathcal {N}}_J$
for any non-meager J. In contrast, we ask the following.
${\mathcal {N}}^*_J={\mathcal {N}}_J$
for any non-meager J. In contrast, we ask the following.
Question 7.3. Can we prove in
![]() $\mathrm {ZFC}$
that there is a non-meager ideal J on
$\mathrm {ZFC}$
that there is a non-meager ideal J on
![]() $\omega $
such that
$\omega $
such that
![]() ${\mathcal {N}}^*_J\neq {\mathcal {N}}_J$
?
${\mathcal {N}}^*_J\neq {\mathcal {N}}_J$
?
Recall that we produced such an example in Lemma 4.11 under the assumption that there is a pair of non-nearly coherent ideals on
![]() $\omega $
. The answer to the previous questions would expand our knowledge about the difference between
$\omega $
. The answer to the previous questions would expand our knowledge about the difference between
![]() ${\mathcal {N}}_J$
and
${\mathcal {N}}_J$
and
![]() ${\mathcal {N}}_K$
for different J and K.
${\mathcal {N}}_K$
for different J and K.
Concerning the cardinal characteristics, we showed that it is possible to have
![]() ${\mathrm {non}}({\mathcal {N}}^*_K)<{\mathrm {non}}({\mathcal {N}}_K)$
and
${\mathrm {non}}({\mathcal {N}}^*_K)<{\mathrm {non}}({\mathcal {N}}_K)$
and
![]() ${\mathrm {cov}}({\mathcal {N}}_K)<{\mathrm {cov}}({\mathcal {N}}^*_K)$
for some non-meager ideal K (in Cohen model, see Corollary 6.5). However, we do not know what happens to the additivities and the cofinalities.
${\mathrm {cov}}({\mathcal {N}}_K)<{\mathrm {cov}}({\mathcal {N}}^*_K)$
for some non-meager ideal K (in Cohen model, see Corollary 6.5). However, we do not know what happens to the additivities and the cofinalities.
Question 7.4. Is it consistent that
![]() ${\mathrm {add}}({\mathcal {N}}_J)$
and
${\mathrm {add}}({\mathcal {N}}_J)$
and
![]() ${\mathrm {add}}({\mathcal {N}}^*_J)$
are different for some non-meager ideal J on
${\mathrm {add}}({\mathcal {N}}^*_J)$
are different for some non-meager ideal J on
![]() $\omega $
? The same is asked for the cofinalities.
$\omega $
? The same is asked for the cofinalities.
Question 7.5. Does
![]() $\mathrm {ZFC}$
prove some inequality between
$\mathrm {ZFC}$
prove some inequality between
![]() ${\mathrm {add}}({\mathcal {N}}_J)$
and
${\mathrm {add}}({\mathcal {N}}_J)$
and
![]() ${\mathrm {add}}({\mathcal {N}}^*_J)$
? The same is asked for the cofinalities.
${\mathrm {add}}({\mathcal {N}}^*_J)$
? The same is asked for the cofinalities.
The second author [Reference Mejía32] has constructed a forcing model where the four cardinal characteristics associated with
![]() ${\mathcal {N}}$
are pairwise different. Cardona [Reference Cardona19] has produced a similar model for
${\mathcal {N}}$
are pairwise different. Cardona [Reference Cardona19] has produced a similar model for
![]() ${\mathcal {E}}$
. In this context, we ask the following.
${\mathcal {E}}$
. In this context, we ask the following.
Question 7.6. Is it consistent with
![]() $\mathrm {ZFC}$
that, for some non-meager (or maximal) ideal J on
$\mathrm {ZFC}$
that, for some non-meager (or maximal) ideal J on
![]() $\omega $
, the four cardinal characteristics associated with
$\omega $
, the four cardinal characteristics associated with
![]() ${\mathcal {N}}_J$
are pairwise different?
${\mathcal {N}}_J$
are pairwise different?
In relation with the cardinal characteristics in Figure 6, to have a complete answer that no other inequality can be proved for the cardinal characteristics associated with our ideals, it remains to solve the following problems.
Question 7.7. Does
![]() $\mathrm {ZFC}$
prove
$\mathrm {ZFC}$
prove
![]() ${\mathfrak {g}}\leq {\mathrm {cof}}({\mathcal {N}}_J)$
for any ideal J on
${\mathfrak {g}}\leq {\mathrm {cof}}({\mathcal {N}}_J)$
for any ideal J on
![]() $\omega $
?
$\omega $
?
Question 7.8. Is it consistent that
![]() ${\mathrm {cov}}({\mathcal {N}}_J)<{\mathfrak {p}}$
for some maximal ideal J?
${\mathrm {cov}}({\mathcal {N}}_J)<{\mathfrak {p}}$
for some maximal ideal J?
Question 7.9. Is it consistent that
![]() $\max \{{\mathfrak {u}},{\mathfrak {i}}\}<{\mathrm {non}}({\mathcal {N}}_J)$
for some maximal ideal J?
$\max \{{\mathfrak {u}},{\mathfrak {i}}\}<{\mathrm {non}}({\mathcal {N}}_J)$
for some maximal ideal J?
Concerning the structure of our ideals, we ask the following.
Question 7.10. What is the intersection of all
![]() ${\mathcal {N}}_J$
? What is the union of all
${\mathcal {N}}_J$
? What is the union of all
![]() ${\mathcal {N}}^*_J$
?
${\mathcal {N}}^*_J$
?
Note that such intersection is
![]() ${\mathcal {N}}_{\min }$
and the union is
${\mathcal {N}}_{\min }$
and the union is
![]() ${\mathcal {N}}^*_{\max }$
, where
${\mathcal {N}}^*_{\max }$
, where
 $$ \begin{align*} {\mathcal{N}}_{\min} & :=\bigcap{\left\{ {{\mathcal{N}}_J} :\, {J \mbox{ maximal ideal}} \right\}},\\ {\mathcal{N}}^*_{\max} & :=\bigcup{\left\{ {{\mathcal{N}}_J} :\, {J \mbox{ maximal ideal}} \right\}}. \end{align*} $$
$$ \begin{align*} {\mathcal{N}}_{\min} & :=\bigcap{\left\{ {{\mathcal{N}}_J} :\, {J \mbox{ maximal ideal}} \right\}},\\ {\mathcal{N}}^*_{\max} & :=\bigcup{\left\{ {{\mathcal{N}}_J} :\, {J \mbox{ maximal ideal}} \right\}}. \end{align*} $$
According to Corollary 4.4, under NCF,
![]() ${\mathcal {N}}_{\min }={\mathcal {N}}^*_{\max }$
. It is curious what would these families be when allowing non-nearly coherent ideals.
${\mathcal {N}}_{\min }={\mathcal {N}}^*_{\max }$
. It is curious what would these families be when allowing non-nearly coherent ideals.
We finish this paper with a brief discussion about strong measure zero sets. Denote by
![]() ${\mathcal {SN}}$
the ideal of strong measure zero subsets of
${\mathcal {SN}}$
the ideal of strong measure zero subsets of
![]() ${{}^\omega 2}$
. We know that
${{}^\omega 2}$
. We know that
![]() ${\mathcal {SN}}\subseteq {\mathcal {N}}$
and
${\mathcal {SN}}\subseteq {\mathcal {N}}$
and
![]() ${\mathcal {E}}\nsubseteq {\mathcal {SN}}$
(because perfect subsets of
${\mathcal {E}}\nsubseteq {\mathcal {SN}}$
(because perfect subsets of
![]() ${{}^\omega 2}$
cannot be in
${{}^\omega 2}$
cannot be in
![]() ${\mathcal {SN}}$
). Under Borel’s conjecture, we have
${\mathcal {SN}}$
). Under Borel’s conjecture, we have
![]() ${\mathcal {SN}}\subseteq {\mathcal {E}}$
, however,
${\mathcal {SN}}\subseteq {\mathcal {E}}$
, however,
![]() ${\mathrm {cov}}({\mathcal {SN}})<{\mathrm {cov}}({\mathcal {E}})$
holds in Cohen’s model [Reference Pawlikowski35] (see also [Reference Bartoszyński and Judah4, Section 8.4A]), which implies
${\mathrm {cov}}({\mathcal {SN}})<{\mathrm {cov}}({\mathcal {E}})$
holds in Cohen’s model [Reference Pawlikowski35] (see also [Reference Bartoszyński and Judah4, Section 8.4A]), which implies
![]() ${\mathcal {SN}}\nsubseteq {\mathcal {E}}$
. This motivates to ask the following.
${\mathcal {SN}}\nsubseteq {\mathcal {E}}$
. This motivates to ask the following.
Question 7.11. Does ZFC prove that there is some non-meager ideal J such that
![]() ${\mathcal {SN}}\subseteq {\mathcal {N}}_J$
, or even
${\mathcal {SN}}\subseteq {\mathcal {N}}_J$
, or even
![]() ${\mathcal {SN}}\subseteq {\mathcal {N}}^*_J$
?
${\mathcal {SN}}\subseteq {\mathcal {N}}^*_J$
?
In the model from Theorem 6.3 this can not happen for some maximal ideals because ZFC proves
![]() ${\mathrm {cov}}({\mathcal {M}}) \leq {\mathrm {non}}({\mathcal {SN}})$
(Miller [Reference Miller34]).
${\mathrm {cov}}({\mathcal {M}}) \leq {\mathrm {non}}({\mathcal {SN}})$
(Miller [Reference Miller34]).
Acknowledgments
The authors thank the participants of Košice set-theoretical seminar, especially Jaroslav Šupina and Miguel Cardona, for very fruitful discussions about this work, and the anonymous referee for the constructive comments.
Funding
The first author was supported by APVV-20-0045 of the Slovak Research and Development Agency, and the second author was supported by the Grant-in-Aid for Early Career Scientists 18K13448 and the Grant-in-Aid for Scientific Research (C) 23K03198, Japan Society for the Promotion of Science.