Article contents
The cofinality of cardinal invariants related to measure and category
Published online by Cambridge University Press: 12 March 2014
Abstract
We prove that the following are consistent with ZFC:
1. 2ω = ℵω1 + #x039A;c = ℵω1 + ΚΒ = ΚU = ω2 (for measure and category simultaneously).
2. 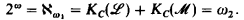 .
.
This concludes the discussion about the cofinality of Κc.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1989
References
REFERENCES
- 5
- Cited by


