Research Article
An independence result in quadratic form theory: Infinitary combinatorics applied to ε-Hermitian spaces
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 689-699
-
- Article
- Export citation
Errata
Errata
-
- Published online by Cambridge University Press:
- 12 March 2014, p. viii
-
- Article
-
- You have access
- Export citation
Research Article
On the strength of the interpretation method
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 305-323
-
- Article
- Export citation
Ultrafilters of character ω1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1-15
-
- Article
- Export citation
A Survey/expository paper
The roots of contemporary Platonism
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1121-1144
-
- Article
- Export citation
Research Article
A jump class of noncappable degrees
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 324-353
-
- Article
- Export citation
On generic elementary embeddings
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 700-707
-
- Article
- Export citation
Abstract hierarchies and degrees
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 16-25
-
- Article
- Export citation
Coding over a measurable cardinal
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1145-1159
-
- Article
- Export citation
Patching ideal families and enforcing reflection
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 26-37
-
- Article
- Export citation
Saturating ultrafilters on N
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 708-718
-
- Article
- Export citation
Equational logic of partial functions under Kleene equality: a complete and an incomplete set of rules
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 354-362
-
- Article
- Export citation
Finite injury and Σ1-induction
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 38-49
-
- Article
- Export citation
On hyper-torre isols
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1160-1166
-
- Article
- Export citation
The structure of algebraically and existentially closed Stone and double Stone algebras
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 363-375
-
- Article
- Export citation
The cofinality of cardinal invariants related to measure and category
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 719-726
-
- Article
- Export citation
A limit on relative genericity in the recursively enumerable sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 376-395
-
- Article
- Export citation
The Σ21 theory of axioms of symmetry
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 727-734
-
- Article
- Export citation
Consistency results about filters and the number of inequivalent growth types
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 50-56
-
- Article
- Export citation
Descriptive set theory over hyperfinite sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1167-1180
-
- Article
- Export citation



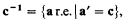
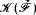 can be obtained as the restriction of a generic embedding of a precipitous ideal. Notice that there are obvious limitations. Thus the ultrapower of
can be obtained as the restriction of a generic embedding of a precipitous ideal. Notice that there are obvious limitations. Thus the ultrapower of 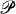 for producing a real R such that
for producing a real R such that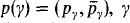 belonging to an initial segment of the cardinals, where
belonging to an initial segment of the cardinals, where 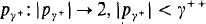 into a subset of
into a subset of 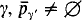 for only a
for only a 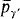 and the need to code extensions of
and the need to code extensions of 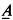 has a model companion. Weispfenning [24], [25] discovered that this model companion is always ℵ
has a model companion. Weispfenning [24], [25] discovered that this model companion is always ℵ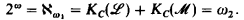 .
.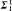 ). In §3 we show
). In §3 we show 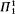 ),
), 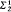 ) and
) and