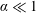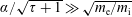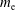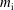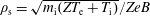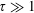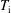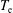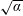Sherwood Fusion Theory Conferences
This JPP Special Issue includes contributions from Sherwood Fusion Theory Conferences from 2019 onwards.
Research Article
An adjoint method for neoclassical stellarator optimization
- Part of:
-
- Journal:
- Journal of Plasma Physics / Volume 85 / Issue 5 / 2019
- Published online by Cambridge University Press:
- 06 September 2019, 795850501
Dependence on ion temperature of shallow-angle magnetic presheaths with adiabatic electrons
- Part of:
-
- Journal:
- Journal of Plasma Physics / Volume 85 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 08 November 2019, 795850601
-
- Article
-
- You have access
- HTML
- Export citation
- NASA ADS Abstract Service
Anomalous losses of energetic particles in the presence of an oscillating radial electric field in fusion plasmas
- Part of:
-
- Journal:
- Journal of Plasma Physics / Volume 86 / Issue 2 / 2020
- Published online by Cambridge University Press:
- 27 April 2020, 795860201
-
- Article
-
- You have access
- HTML
- Export citation
- NASA ADS Abstract Service