1 Introduction
Across a wide variety of accreting astrophysical systems, the inflow of matter is thought to rely on turbulent angular-momentum transport driven by the magnetorotational instability (MRI; Balbus & Hawley Reference Balbus and Hawley1991, Reference Balbus and Hawley1998). The majority of works studying the MRI, in particular its saturation into turbulence (e.g. Hawley, Gammie & Balbus Reference Hawley, Gammie and Balbus1995; Hawley, Balbus & Stone Reference Hawley, Balbus and Stone2001; Ryan et al.
Reference Ryan, Gammie, Fromang and Kestener2017), have been based on magnetohydrodynamics (MHD). They thus implicitly assume that the collisional mean free path of gas particles is small in comparison to the scales of all fluid motions. However, this assumption can be far from valid in many accreting systems. For instance, in radiatively inefficient accretion flows onto supermassive black holes (RIAFs; see Narayan, Mahadevan & Quataert Reference Narayan, Mahadevan, Quataert, Abramowicz, Björnsson and Pringle1998; Hawley & Balbus Reference Hawley and Balbus2002; Quataert Reference Quataert2003; Yuan & Narayan Reference Yuan and Narayan2014), a large portion of the gravitational potential energy of the infalling gas is converted directly into thermal energy, suggesting ion temperatures
![]() $T_{i}\sim 10^{12}~\text{K}$
with corresponding ion collisional mean free paths that are orders of magnitude larger than the system size.
$T_{i}\sim 10^{12}~\text{K}$
with corresponding ion collisional mean free paths that are orders of magnitude larger than the system size.
As shown by Quataert, Dorland & Hammett (Reference Quataert, Dorland and Hammett2002) (hereafter Reference Quataert, Dorland and HammettQ02), Sharma, Hammett & Quataert (Reference Sharma, Hammett and Quataert2003) and Balbus (Reference Balbus2004), the linear magnetorotational instability still exists in collisionless and weakly collisional plasmas. This kinetic MRI (KMRI) has seen subsequent theoretical attention. As well as extensions to the original linear analyses using either fully kinetic treatments (Sharma et al. Reference Sharma, Hammett and Quataert2003; Heinemann & Quataert Reference Heinemann and Quataert2014; Quataert, Heinemann & Spitkovsky Reference Quataert, Heinemann and Spitkovsky2015) or fluid models (Ferraro Reference Ferraro2007; Rosin & Mestel Reference Rosin and Mestel2012), various works have explored turbulent transport in the fully nonlinear regime, generally finding behaviour that bears a strong similarity to that seen in standard resistive MHD. Sharma et al. (Reference Sharma, Hammett, Quataert and Stone2006) (hereafter Reference Sharma, Hammett, Quataert and StoneS06) was the first to study MRI turbulence in this regime using a kinetically motivated fluid closure, an approach that has been followed in a variety of works since (e.g. Sharma et al. Reference Sharma, Quataert, Hammett and Stone2007; Chandra et al. Reference Chandra, Gammie, Foucart and Quataert2015; Foucart et al. Reference Foucart, Chandra, Gammie and Quataert2015). Recently, it has become possible to study the MRI using truly kinetic particle-in-cell (PIC) methods, both in two dimensions (Riquelme et al. Reference Riquelme, Quataert, Sharma and Spitkovsky2012; Hoshino Reference Hoshino2013; Kunz, Stone & Bai Reference Kunz, Stone and Bai2014b ) and three dimensions (Hoshino Reference Hoshino2015; Kunz, Stone & Quataert Reference Kunz, Stone and Quataert2016). Most notably, in Kunz et al. (Reference Kunz, Stone and Quataert2016), a fully collisionless plasma was seen to develop into MRI turbulence with strong similarities to that seen in comparable MHD calculations (or, even more so, similarities to the model of Reference Sharma, Hammett, Quataert and StoneS06), providing a fascinating example of a fully collisionless plasma behaving as a collisional fluid.
In this paper, we explore the regime between fully nonlinear turbulence and the linear KMRI. Our purpose is to move towards understanding the nonlinear saturation of the KMRI, in particular the similarities with, and differences to, the standard MRI. Our philosophy is to examine the simplest (and, hopefully, the most significant) modifications to MHD. With this in mind, we consider both the kinetically motivated Landau-fluid (LF) model used by Reference Sharma, Hammett, Quataert and StoneS06 and ‘Braginskii’ MHD (Braginskii Reference Braginskii1965), which is valid in the weakly collisional regime. We study two interlinked effects, each of which could have a strong influence on how the KMRI saturates into turbulence. The first effect is the pressure anisotropy (
![]() $\unicode[STIX]{x0394}p$
) driven by growing KMRI modes. This can nonlinearly affect the modes’ evolution (even in one dimension) at amplitudes far smaller – by a factor
$\unicode[STIX]{x0394}p$
) driven by growing KMRI modes. This can nonlinearly affect the modes’ evolution (even in one dimension) at amplitudes far smaller – by a factor
![]() ${\sim}\unicode[STIX]{x1D6FD}$
, the ratio of thermal to magnetic pressure – than occurs in a standard compressible gas with isotropic pressure. It is important to understand the effect of this nonlinearity, because it is these anisotropy-modified KMRI modes that will be disrupted at large amplitudes and excite turbulence. The second effect that we study is the nonlinear disruption of KMRI modes by parasitic modes, which are thought to govern the transition into strong turbulence (Goodman & Xu Reference Goodman and Xu1994; Latter, Lesaffre & Balbus Reference Latter, Lesaffre and Balbus2009; Pessah & Goodman Reference Pessah and Goodman2009; Latter, Fromang & Gressel Reference Latter, Fromang and Gressel2010; Longaretti & Lesur Reference Longaretti and Lesur2010). MHD parasitic modes are Kelvin–Helmholtz and tearing modes that feed off strong gradients in the large-amplitude MRI ‘channel’ mode.Footnote
1
A significant difference in parasitic-mode growth rates in a collisionless plasma (compared to MHD) would suggest that the saturation of the KMRI into turbulence would also be significantly modified, perhaps with important implications for KMRI-driven turbulence.
${\sim}\unicode[STIX]{x1D6FD}$
, the ratio of thermal to magnetic pressure – than occurs in a standard compressible gas with isotropic pressure. It is important to understand the effect of this nonlinearity, because it is these anisotropy-modified KMRI modes that will be disrupted at large amplitudes and excite turbulence. The second effect that we study is the nonlinear disruption of KMRI modes by parasitic modes, which are thought to govern the transition into strong turbulence (Goodman & Xu Reference Goodman and Xu1994; Latter, Lesaffre & Balbus Reference Latter, Lesaffre and Balbus2009; Pessah & Goodman Reference Pessah and Goodman2009; Latter, Fromang & Gressel Reference Latter, Fromang and Gressel2010; Longaretti & Lesur Reference Longaretti and Lesur2010). MHD parasitic modes are Kelvin–Helmholtz and tearing modes that feed off strong gradients in the large-amplitude MRI ‘channel’ mode.Footnote
1
A significant difference in parasitic-mode growth rates in a collisionless plasma (compared to MHD) would suggest that the saturation of the KMRI into turbulence would also be significantly modified, perhaps with important implications for KMRI-driven turbulence.
Our main results are twofold. First, once the KMRI channel mode amplitude
![]() $\unicode[STIX]{x1D6FF}B$
surpasses the strength of the background field
$\unicode[STIX]{x1D6FF}B$
surpasses the strength of the background field
![]() $B_{0}$
, its evolution always reverts to MHD-like behaviour. In particular, because of the pressure-anisotropy-limiting effects of kinetic microinstabilities (Schekochihin et al.
Reference Schekochihin, Cowley, Kulsrud, Rosin and Heinemann2008; Kunz et al.
Reference Kunz, Schekochihin, Chen, Abel and Cowley2015) and the specific form of MRI modes, the pressure anisotropy has very little effect on mode evolution once
$B_{0}$
, its evolution always reverts to MHD-like behaviour. In particular, because of the pressure-anisotropy-limiting effects of kinetic microinstabilities (Schekochihin et al.
Reference Schekochihin, Cowley, Kulsrud, Rosin and Heinemann2008; Kunz et al.
Reference Kunz, Schekochihin, Chen, Abel and Cowley2015) and the specific form of MRI modes, the pressure anisotropy has very little effect on mode evolution once
![]() $\unicode[STIX]{x1D6FF}B\gtrsim B_{0}$
. The MRI modes are then approximate nonlinear solutions of the Landau-fluid or Braginskii models until they reach very large amplitudes. However, at moderate mode amplitudes
$\unicode[STIX]{x1D6FF}B\gtrsim B_{0}$
. The MRI modes are then approximate nonlinear solutions of the Landau-fluid or Braginskii models until they reach very large amplitudes. However, at moderate mode amplitudes
![]() $\unicode[STIX]{x1D6FF}B\lesssim B_{0}$
, the effect of pressure anisotropy can be significant; for example, it causes strong modifications to the KMRI in the presence of a background azimuthal fieldFootnote
2
at amplitudes well below where it would saturate into turbulence. Our second result is that there is not a strong difference in parasitic-mode growth rates between the kinetic and MHD models, which indicates that modes can grow to similar amplitudes before being disrupted in collisionless and collisional systems. Together these conclusions suggest that the saturation of MRI modes into turbulence in high-
$\unicode[STIX]{x1D6FF}B\lesssim B_{0}$
, the effect of pressure anisotropy can be significant; for example, it causes strong modifications to the KMRI in the presence of a background azimuthal fieldFootnote
2
at amplitudes well below where it would saturate into turbulence. Our second result is that there is not a strong difference in parasitic-mode growth rates between the kinetic and MHD models, which indicates that modes can grow to similar amplitudes before being disrupted in collisionless and collisional systems. Together these conclusions suggest that the saturation of MRI modes into turbulence in high-
![]() $\unicode[STIX]{x1D6FD}$
collisionless and weakly collisional regimes will be similar to what occurs in a collisional (MHD) plasma. This appears to be the case in the simulations that have been run up to now, including those that do not rely on fluid closure schemes (Riquelme et al.
Reference Riquelme, Quataert, Sharma and Spitkovsky2012; Hoshino Reference Hoshino2013, Reference Hoshino2015; Kunz et al.
Reference Kunz, Stone and Quataert2016).
$\unicode[STIX]{x1D6FD}$
collisionless and weakly collisional regimes will be similar to what occurs in a collisional (MHD) plasma. This appears to be the case in the simulations that have been run up to now, including those that do not rely on fluid closure schemes (Riquelme et al.
Reference Riquelme, Quataert, Sharma and Spitkovsky2012; Hoshino Reference Hoshino2013, Reference Hoshino2015; Kunz et al.
Reference Kunz, Stone and Quataert2016).
In some ways, the results of this work will primarily be of interest for understanding and designing future three-dimensional (3-D) fully kinetic simulations of MRI turbulence. Such simulations are the only clear method available to explore the collisionless accretion flows without ad hoc assumptions, but are very demanding computationally. The primary difficulty arises from the enormous scale separation in RIAFs between the ion gyrofrequency
![]() $\unicode[STIX]{x1D6FA}_{i}$
(which must be resolved in a kinetic code) and the disk rotation frequency
$\unicode[STIX]{x1D6FA}_{i}$
(which must be resolved in a kinetic code) and the disk rotation frequency
![]() $\unicode[STIX]{x1D6FA}$
. Simulations are necessarily limited to modest values of
$\unicode[STIX]{x1D6FA}$
. Simulations are necessarily limited to modest values of
![]() $\unicode[STIX]{x1D6FA}_{i}/\unicode[STIX]{x1D6FA}$
, and it is thus crucial to understand some of the basic differences between the MRI and KMRI in designing and analysing simulations, so as to ensure that observed effects are not an artefact of limited scale separation. To add to these difficulties, our understanding of the processes governing even the simplest MHD MRI turbulence remains somewhat limited (e.g. see Fromang et al.
Reference Fromang, Papaloizou, Lesur and Heinemann2007; Lesur & Longaretti Reference Lesur and Longaretti2007; Fromang & Stone Reference Fromang and Stone2009; Blackman Reference Blackman2012; Simon, Beckwith & Armitage Reference Simon, Beckwith and Armitage2012; Meheut et al.
Reference Meheut, Fromang, Lesur, Joos and Longaretti2015; Squire & Bhattacharjee Reference Squire and Bhattacharjee2016).
$\unicode[STIX]{x1D6FA}_{i}/\unicode[STIX]{x1D6FA}$
, and it is thus crucial to understand some of the basic differences between the MRI and KMRI in designing and analysing simulations, so as to ensure that observed effects are not an artefact of limited scale separation. To add to these difficulties, our understanding of the processes governing even the simplest MHD MRI turbulence remains somewhat limited (e.g. see Fromang et al.
Reference Fromang, Papaloizou, Lesur and Heinemann2007; Lesur & Longaretti Reference Lesur and Longaretti2007; Fromang & Stone Reference Fromang and Stone2009; Blackman Reference Blackman2012; Simon, Beckwith & Armitage Reference Simon, Beckwith and Armitage2012; Meheut et al.
Reference Meheut, Fromang, Lesur, Joos and Longaretti2015; Squire & Bhattacharjee Reference Squire and Bhattacharjee2016).
The remainder of the paper is organized as follows. In § 2 we introduce the models used throughout our work and the numerical methods used to solve them (§ 2.2). Because the effects that arise due to pressure anisotropy may be unfamiliar to many readers, we provide a brief account in § 2.3 of the primary differences between each model and MHD. One-dimensional nonlinearities arising due to self-generated pressure anisotropies are then treated in § 3, starting with an overview of the linear physics, and then treating the pure-vertical-field KMRI (§ 3.2) and azimuthal-field KMRI (§ 3.3) separately. An overview of these results is given in § 3.4. We then consider the evolution of parasitic modes in § 4, starting with linear calculations on sinusoidal background profiles (§ 4.1) and then showing fully nonlinear calculations using the Zeus code used by Reference Sharma, Hammett, Quataert and StoneS06 (§ 4.2). This section is deliberately kept brief, due to the null result that nonlinear saturation is not strongly affected by the pressure anisotropy. A discussion of kinetic effects neglected in our model is given in § 5. We then combine our results with those from previous kinetics simulations of mirror and magnetorotational instabilities to provide guidance for the design of future simulations of KMRI turbulence (§ 6). Finally, we conclude with a summary in § 7.
2 Governing equations: the effects of pressure anisotropy
Our philosophy throughout this work is to consider the simplest and most general modifications to MRI evolution on the largest (MHD) scales due to kinetic physics. We anticipate (but cannot prove) that these are the most important kinetic modifications to the MRI. We thus focus on the development of a gyrotropic pressure anisotropy – i.e. a pressure tensor that differs in the directions parallel (
![]() $p_{\Vert }$
) and perpendicular (
$p_{\Vert }$
) and perpendicular (
![]() $p_{\bot }$
) to the magnetic-field lines, but that is unchanged by rotations about the field line. This pressure anisotropy,
$p_{\bot }$
) to the magnetic-field lines, but that is unchanged by rotations about the field line. This pressure anisotropy,
![]() $\unicode[STIX]{x0394}p\equiv p_{\bot }-p_{\Vert }$
, causes an additional stress in the momentum equation, which can nonlinearly affect the MRI modes at much lower amplitudes than occurs in standard MHD. The gyrotropic approximation is generally valid when the magnetic field varies on spatial and temporal scales much larger than the ion gyroradius and inverse gyrofrequency.
$\unicode[STIX]{x0394}p\equiv p_{\bot }-p_{\Vert }$
, causes an additional stress in the momentum equation, which can nonlinearly affect the MRI modes at much lower amplitudes than occurs in standard MHD. The gyrotropic approximation is generally valid when the magnetic field varies on spatial and temporal scales much larger than the ion gyroradius and inverse gyrofrequency.
2.1 Basic equations and closure models
Our equations are obtained as follows. A small patch of an accretion disc, co-orbiting with a fiducial point
![]() $R_{0}$
in the mid-plane of the unperturbed disc at an angular velocity
$R_{0}$
in the mid-plane of the unperturbed disc at an angular velocity
![]() $\unicode[STIX]{x1D734}=\unicode[STIX]{x1D6FA}\hat{\boldsymbol{z}}$
, is represented in Cartesian coordinates with the
$\unicode[STIX]{x1D734}=\unicode[STIX]{x1D6FA}\hat{\boldsymbol{z}}$
, is represented in Cartesian coordinates with the
![]() $x$
and
$x$
and
![]() $y$
directions corresponding to the radial and azimuthal directions, respectively. Differential rotation is accounted for by including the Coriolis force and by imposing a background linear shear flow,
$y$
directions corresponding to the radial and azimuthal directions, respectively. Differential rotation is accounted for by including the Coriolis force and by imposing a background linear shear flow,
![]() $\boldsymbol{U}_{0}=-Sx\hat{\boldsymbol{y}}$
, where
$\boldsymbol{U}_{0}=-Sx\hat{\boldsymbol{y}}$
, where
![]() $S\equiv -\text{d}\unicode[STIX]{x1D6FA}/\text{d}\ln R_{0}>0$
is the shear frequency; Keplerian rotation yields
$S\equiv -\text{d}\unicode[STIX]{x1D6FA}/\text{d}\ln R_{0}>0$
is the shear frequency; Keplerian rotation yields
![]() $S=(3/2)\unicode[STIX]{x1D6FA}$
. The evolutionary equations for the first three moments of the plasma distribution function are then (Chew, Goldberger & Low Reference Chew, Goldberger and Low1956; Kulsrud Reference Kulsrud, Rosenbluth and Sagdeev1983; Schekochihin et al.
Reference Schekochihin, Cowley, Rincon and Rosin2010),
$S=(3/2)\unicode[STIX]{x1D6FA}$
. The evolutionary equations for the first three moments of the plasma distribution function are then (Chew, Goldberger & Low Reference Chew, Goldberger and Low1956; Kulsrud Reference Kulsrud, Rosenbluth and Sagdeev1983; Schekochihin et al.
Reference Schekochihin, Cowley, Rincon and Rosin2010),
where
![]() $\text{d}/\text{d}t\equiv \unicode[STIX]{x2202}/\unicode[STIX]{x2202}t+\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}$
is the convective derivative. The velocity
$\text{d}/\text{d}t\equiv \unicode[STIX]{x2202}/\unicode[STIX]{x2202}t+\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}$
is the convective derivative. The velocity
![]() $\boldsymbol{u}$
in (2.1)–(2.5) includes both the background shear flow
$\boldsymbol{u}$
in (2.1)–(2.5) includes both the background shear flow
![]() $\boldsymbol{U}_{0}$
and perturbations on top of this
$\boldsymbol{U}_{0}$
and perturbations on top of this
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{u}$
(e.g. the MRI). The other symbols have their usual meanings:
$\unicode[STIX]{x1D6FF}\boldsymbol{u}$
(e.g. the MRI). The other symbols have their usual meanings:
![]() $\unicode[STIX]{x1D70C}$
is the mass density,
$\unicode[STIX]{x1D70C}$
is the mass density,
![]() $\boldsymbol{B}$
is the magnetic field,
$\boldsymbol{B}$
is the magnetic field,
![]() $\unicode[STIX]{x1D708}_{c}$
is the particle collision frequency, while
$\unicode[STIX]{x1D708}_{c}$
is the particle collision frequency, while
![]() $B\equiv |\boldsymbol{B}|$
and
$B\equiv |\boldsymbol{B}|$
and
![]() $\hat{\boldsymbol{b}}\equiv \boldsymbol{B}/B$
denote the magnetic-field strength and direction (note that
$\hat{\boldsymbol{b}}\equiv \boldsymbol{B}/B$
denote the magnetic-field strength and direction (note that
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\hat{\boldsymbol{b}}\hat{\boldsymbol{b}}B^{2})$
is simply
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\hat{\boldsymbol{b}}\hat{\boldsymbol{b}}B^{2})$
is simply
![]() $\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{B}$
). The pressures perpendicular and parallel to
$\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{B}$
). The pressures perpendicular and parallel to
![]() $\hat{\boldsymbol{b}}$
are
$\hat{\boldsymbol{b}}$
are
![]() $p_{\bot }$
and
$p_{\bot }$
and
![]() $p_{\Vert }$
respectively, while
$p_{\Vert }$
respectively, while
![]() $q_{\bot }$
and
$q_{\bot }$
and
![]() $q_{\Vert }$
denote the fluxes of perpendicular and parallel heat in the direction parallel to
$q_{\Vert }$
denote the fluxes of perpendicular and parallel heat in the direction parallel to
![]() $\hat{\boldsymbol{b}}$
. Note that
$\hat{\boldsymbol{b}}$
. Note that
![]() $p_{\bot }$
and
$p_{\bot }$
and
![]() $p_{\Vert }$
in (2.2) should in principle be summed over both particle species (with separate pressures for each species), while
$p_{\Vert }$
in (2.2) should in principle be summed over both particle species (with separate pressures for each species), while
![]() $\unicode[STIX]{x1D70C}$
and
$\unicode[STIX]{x1D70C}$
and
![]() $\boldsymbol{u}$
in (2.1)–(2.3) are the ion density and flow velocity. For simplicity, in this work we solve only the ion pressure equations (i.e.
$\boldsymbol{u}$
in (2.1)–(2.3) are the ion density and flow velocity. For simplicity, in this work we solve only the ion pressure equations (i.e.
![]() $p_{\bot }=p_{\bot ,i}$
,
$p_{\bot }=p_{\bot ,i}$
,
![]() $p_{\Vert }=p_{\Vert ,i}$
), which is justified in the limit of cold electrons (as expected in RIAFs, e.g. Sharma et al.
Reference Sharma, Quataert, Hammett and Stone2007). We have also neglected non-ideal corrections to the induction equation (2.3) (e.g. the Hall term), which is appropriate given our neglect of finite Larmor radius (FLR) effects in (2.2) (we will, however, include a hyper-resistivity term in equation (2.3) for numerical reasons; see § 2.2). For convenience, we define the dimensionless anisotropy
$p_{\Vert }=p_{\Vert ,i}$
), which is justified in the limit of cold electrons (as expected in RIAFs, e.g. Sharma et al.
Reference Sharma, Quataert, Hammett and Stone2007). We have also neglected non-ideal corrections to the induction equation (2.3) (e.g. the Hall term), which is appropriate given our neglect of finite Larmor radius (FLR) effects in (2.2) (we will, however, include a hyper-resistivity term in equation (2.3) for numerical reasons; see § 2.2). For convenience, we define the dimensionless anisotropy
![]() $\unicode[STIX]{x1D6E5}\equiv \unicode[STIX]{x0394}p/p_{0}$
, where
$\unicode[STIX]{x1D6E5}\equiv \unicode[STIX]{x0394}p/p_{0}$
, where
![]() $p_{0}=(p_{\bot }+2p_{\Vert })/3$
is the total thermal pressure, as well as the ratio of thermal to magnetic pressure
$p_{0}=(p_{\bot }+2p_{\Vert })/3$
is the total thermal pressure, as well as the ratio of thermal to magnetic pressure
![]() $\unicode[STIX]{x1D6FD}\equiv 8\unicode[STIX]{x03C0}p_{0}/B^{2}$
, the Alfvén speed
$\unicode[STIX]{x1D6FD}\equiv 8\unicode[STIX]{x03C0}p_{0}/B^{2}$
, the Alfvén speed
![]() $v_{A}=B/\sqrt{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}}$
and its
$v_{A}=B/\sqrt{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}}$
and its
![]() $\hat{\boldsymbol{z}}$
component
$\hat{\boldsymbol{z}}$
component
![]() $v_{Az}=B_{z}/\sqrt{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}}$
, the sound speed
$v_{Az}=B_{z}/\sqrt{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}}$
, the sound speed
![]() $c_{s}=\sqrt{p_{0}/\unicode[STIX]{x1D70C}}$
and the parallel sound speed
$c_{s}=\sqrt{p_{0}/\unicode[STIX]{x1D70C}}$
and the parallel sound speed
![]() $c_{s\Vert }=\sqrt{p_{\Vert }/\unicode[STIX]{x1D70C}}$
. The double-dot notation used in (2.4)–(2.5) and throughout this work is
$c_{s\Vert }=\sqrt{p_{\Vert }/\unicode[STIX]{x1D70C}}$
. The double-dot notation used in (2.4)–(2.5) and throughout this work is
![]() $\hat{\boldsymbol{b}}\hat{\boldsymbol{b}}\,\boldsymbol{ : }\,\unicode[STIX]{x1D735}\boldsymbol{u}\equiv \sum _{i,j}b_{i}b_{j}\unicode[STIX]{x2202}_{i}u_{j}$
.
$\hat{\boldsymbol{b}}\hat{\boldsymbol{b}}\,\boldsymbol{ : }\,\unicode[STIX]{x1D735}\boldsymbol{u}\equiv \sum _{i,j}b_{i}b_{j}\unicode[STIX]{x2202}_{i}u_{j}$
.
In their present form, equations (2.1)–(2.5) are not closed, due to the presence of the unspecified heat fluxes,
![]() $q_{\bot }$
and
$q_{\bot }$
and
![]() $q_{\Vert }$
. These must be either specified using a closure scheme, neglected or solved for using the full kinetic equations. In this work we consider three closures for
$q_{\Vert }$
. These must be either specified using a closure scheme, neglected or solved for using the full kinetic equations. In this work we consider three closures for
![]() $q_{\bot }$
and
$q_{\bot }$
and
![]() $q_{\Vert }$
(or equivalently, three approximations to (2.4)–(2.5)). These will be seen to lead to quite different behaviour in solutions of (2.1)–(2.5). They are:
$q_{\Vert }$
(or equivalently, three approximations to (2.4)–(2.5)). These will be seen to lead to quite different behaviour in solutions of (2.1)–(2.5). They are:
Collisionless Landau-fluid closure. Landau-fluid (LF) closures have been used extensively in the fusion community (Hammett & Perkins Reference Hammett and Perkins1990; Hammett, Dorland & Perkins Reference Hammett, Dorland and Perkins1992; Snyder, Hammett & Dorland Reference Snyder, Hammett and Dorland1997) and, to a lesser degree, for astrophysical applications (Reference Sharma, Hammett, Quataert and StoneS06; Sharma et al.
Reference Sharma, Quataert, Hammett and Stone2007). They are particularly well suited for modelling collisionless (
![]() $\unicode[STIX]{x1D708}_{c}=0$
) plasmas. In the LF closure, the heat fluxes,
$\unicode[STIX]{x1D708}_{c}=0$
) plasmas. In the LF closure, the heat fluxes,
are constructed to replicate the effects of linear Landau damping. Here
![]() $\unicode[STIX]{x1D735}_{\Vert }\equiv \hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}$
denotes the gradient parallel to the field and
$\unicode[STIX]{x1D735}_{\Vert }\equiv \hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}$
denotes the gradient parallel to the field and
![]() $|k_{\Vert }|$
denotes the wavenumber parallel to the field, which must be considered as an operator because it appears in the denominator of (2.6)–(2.7). The forms of the heat fluxes in (2.6)–(2.7) accurately reproduce the true kinetic growth rates and frequencies for a variety of large-scale (MHD) modes, including the MRI (Reference Quataert, Dorland and HammettQ02; Sharma et al.
Reference Sharma, Hammett and Quataert2003). We refer the reader to Snyder et al. (Reference Snyder, Hammett and Dorland1997) and Reference Sharma, Hammett, Quataert and StoneS06 for more information.
$|k_{\Vert }|$
denotes the wavenumber parallel to the field, which must be considered as an operator because it appears in the denominator of (2.6)–(2.7). The forms of the heat fluxes in (2.6)–(2.7) accurately reproduce the true kinetic growth rates and frequencies for a variety of large-scale (MHD) modes, including the MRI (Reference Quataert, Dorland and HammettQ02; Sharma et al.
Reference Sharma, Hammett and Quataert2003). We refer the reader to Snyder et al. (Reference Snyder, Hammett and Dorland1997) and Reference Sharma, Hammett, Quataert and StoneS06 for more information.
Weakly collisional ‘Braginskii’ closure. In the Braginskii regime,
![]() $|\unicode[STIX]{x1D735}\boldsymbol{u}|\ll \unicode[STIX]{x1D708}_{c}$
(Braginskii Reference Braginskii1965), the pressure anisotropy is strongly influenced by collisional relaxation. We thus neglect
$|\unicode[STIX]{x1D735}\boldsymbol{u}|\ll \unicode[STIX]{x1D708}_{c}$
(Braginskii Reference Braginskii1965), the pressure anisotropy is strongly influenced by collisional relaxation. We thus neglect
![]() $\text{d}_{t}p_{\bot }$
and
$\text{d}_{t}p_{\bot }$
and
![]() $\text{d}_{t}p_{\Vert }$
in (2.4)–(2.5) and balance the double-adiabatic production of pressure anisotropy (the
$\text{d}_{t}p_{\Vert }$
in (2.4)–(2.5) and balance the double-adiabatic production of pressure anisotropy (the
![]() $\hat{\boldsymbol{b}}\hat{\boldsymbol{b}}\,\boldsymbol{ : }\,\unicode[STIX]{x1D735}\boldsymbol{u}$
and
$\hat{\boldsymbol{b}}\hat{\boldsymbol{b}}\,\boldsymbol{ : }\,\unicode[STIX]{x1D735}\boldsymbol{u}$
and
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}$
terms) against its collisional relaxation (the
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}$
terms) against its collisional relaxation (the
![]() $\unicode[STIX]{x1D708}_{c}\unicode[STIX]{x0394}p$
terms) to find
$\unicode[STIX]{x1D708}_{c}\unicode[STIX]{x0394}p$
terms) to find
where we have also used the fact that
![]() $\unicode[STIX]{x1D708}_{c}/|\unicode[STIX]{x1D735}\boldsymbol{u}|\gg 1$
implies
$\unicode[STIX]{x1D708}_{c}/|\unicode[STIX]{x1D735}\boldsymbol{u}|\gg 1$
implies
![]() $\unicode[STIX]{x0394}p\ll p_{0}$
. (For
$\unicode[STIX]{x0394}p\ll p_{0}$
. (For
![]() $\unicode[STIX]{x1D6FD}\gg 1$
, the
$\unicode[STIX]{x1D6FD}\gg 1$
, the
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}$
term can also be neglected.) When inserted into the momentum equation (2.2), equation (2.8) has the form of an anisotropic viscous stress, and is thus referred to as ‘Braginskii viscosity’ (or Braginskii MHD for the full set of equations). Note that we have neglected heat fluxes in arriving at (2.8), a simplification that is rigorously obtained if
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}$
term can also be neglected.) When inserted into the momentum equation (2.2), equation (2.8) has the form of an anisotropic viscous stress, and is thus referred to as ‘Braginskii viscosity’ (or Braginskii MHD for the full set of equations). Note that we have neglected heat fluxes in arriving at (2.8), a simplification that is rigorously obtained if
![]() $\unicode[STIX]{x1D708}_{c}/|\unicode[STIX]{x1D735}\boldsymbol{u}|\gg \unicode[STIX]{x1D6FD}^{1/2}$
(the ‘high-collisionality’ regime). On the other hand, if
$\unicode[STIX]{x1D708}_{c}/|\unicode[STIX]{x1D735}\boldsymbol{u}|\gg \unicode[STIX]{x1D6FD}^{1/2}$
(the ‘high-collisionality’ regime). On the other hand, if
![]() $\unicode[STIX]{x1D708}_{c}/|\unicode[STIX]{x1D735}\boldsymbol{u}|\ll \unicode[STIX]{x1D6FD}^{1/2}$
(the ‘moderate-collisionality’ regime), the heat fluxes are strong over the time scales of the motion (Mikhailovskii & Tsypin Reference Mikhailovskii and Tsypin1971), and their contribution to the (ion) pressure anisotropy must be retained. (See § B.4 for further discussion.) In this case, there is no simple closure that can be devised (e.g. see appendix B of Squire, Schekochihin & Quataert Reference Squire, Schekochihin and Quataert2017) and it is usually easier to consider the full LF system.
$\unicode[STIX]{x1D708}_{c}/|\unicode[STIX]{x1D735}\boldsymbol{u}|\ll \unicode[STIX]{x1D6FD}^{1/2}$
(the ‘moderate-collisionality’ regime), the heat fluxes are strong over the time scales of the motion (Mikhailovskii & Tsypin Reference Mikhailovskii and Tsypin1971), and their contribution to the (ion) pressure anisotropy must be retained. (See § B.4 for further discussion.) In this case, there is no simple closure that can be devised (e.g. see appendix B of Squire, Schekochihin & Quataert Reference Squire, Schekochihin and Quataert2017) and it is usually easier to consider the full LF system.
Double-adiabatic closure. The double-adiabatic, or Chew–Goldberger–Low (CGL), closure (Chew et al.
Reference Chew, Goldberger and Low1956) simply involves setting
![]() $q_{\bot }=q_{\Vert }=0$
. This approximation is far from justified for subsonic motions in the high-
$q_{\bot }=q_{\Vert }=0$
. This approximation is far from justified for subsonic motions in the high-
![]() $\unicode[STIX]{x1D6FD}$
plasmas considered here; however, the closure is useful for comparison with the LF closure by virtue of its relative simplicity. It has also been employed in a variety of previous computational studies (e.g. Reference Sharma, Hammett, Quataert and StoneS06; Kowal, Falceta-Gonçalves & Lazarian Reference Kowal, Falceta-Gonçalves and Lazarian2011, Santos-Lima et al.
Reference Santos-Lima, de Gouveia Dal Pino, Kowal, Falceta-Gonçalves, Lazarian and Nakwacki2014), and so it is worthwhile to diagnose the model’s successes and limitations.
$\unicode[STIX]{x1D6FD}$
plasmas considered here; however, the closure is useful for comparison with the LF closure by virtue of its relative simplicity. It has also been employed in a variety of previous computational studies (e.g. Reference Sharma, Hammett, Quataert and StoneS06; Kowal, Falceta-Gonçalves & Lazarian Reference Kowal, Falceta-Gonçalves and Lazarian2011, Santos-Lima et al.
Reference Santos-Lima, de Gouveia Dal Pino, Kowal, Falceta-Gonçalves, Lazarian and Nakwacki2014), and so it is worthwhile to diagnose the model’s successes and limitations.
An important caveat for each of these approximations to (2.4)–(2.5) relates to plasma microinstabilities. For our purposes, given the focus of this work on the high-
![]() $\unicode[STIX]{x1D6FD}$
regime, the most significant of these are the firehose instability (Rosenbluth Reference Rosenbluth1956; Chandrasekhar, Kaufman & Watson Reference Chandrasekhar, Kaufman and Watson1958; Parker Reference Parker1958; Yoon, Wu & de Assis Reference Yoon, Wu and de Assis1993), which is excited if
$\unicode[STIX]{x1D6FD}$
regime, the most significant of these are the firehose instability (Rosenbluth Reference Rosenbluth1956; Chandrasekhar, Kaufman & Watson Reference Chandrasekhar, Kaufman and Watson1958; Parker Reference Parker1958; Yoon, Wu & de Assis Reference Yoon, Wu and de Assis1993), which is excited if
and the mirror instability (Hasegawa Reference Hasegawa1969; Southwood & Kivelson Reference Southwood and Kivelson1993; Hellinger Reference Hellinger2007), which is excited if
(There are corrections to these
![]() $\unicode[STIX]{x1D6FD}$
-dependent thresholds that arise from particle resonances and depend on the specific form of the distribution function; see, e.g. Klein & Howes Reference Klein and Howes2015.) Important aspects of these instabilities (e.g. their regularization at small scales or particle scattering in their nonlinear evolution) are not captured by the closures we employ here, and kinetic calculations are needed to correctly understand their saturation. There have been a variety of recent works in this vein (Hellinger & Trávníček Reference Hellinger and Trávníček2008; Schekochihin et al.
Reference Schekochihin, Cowley, Kulsrud, Rosin and Heinemann2008; Rosin et al.
Reference Rosin, Schekochihin, Rincon and Cowley2011; Kunz, Schekochihin & Stone Reference Kunz, Schekochihin and Stone2014a
; Hellinger et al.
Reference Hellinger, Matteini, Landi, Verdini, Franci and Trávníček2015; Rincon, Schekochihin & Cowley Reference Rincon, Schekochihin and Cowley2015; Riquelme, Quataert & Verscharen Reference Riquelme, Quataert and Verscharen2015; Sironi & Narayan Reference Sironi and Narayan2015; Melville, Schekochihin & Kunz Reference Melville, Schekochihin and Kunz2016; Riquelme, Quataert & Verscharen Reference Riquelme, Quataert and Verscharen2016), which have shown that these microinstabilities generally act to pin the pressure anisotropy at the marginal stability limits. Interestingly, when
$\unicode[STIX]{x1D6FD}$
-dependent thresholds that arise from particle resonances and depend on the specific form of the distribution function; see, e.g. Klein & Howes Reference Klein and Howes2015.) Important aspects of these instabilities (e.g. their regularization at small scales or particle scattering in their nonlinear evolution) are not captured by the closures we employ here, and kinetic calculations are needed to correctly understand their saturation. There have been a variety of recent works in this vein (Hellinger & Trávníček Reference Hellinger and Trávníček2008; Schekochihin et al.
Reference Schekochihin, Cowley, Kulsrud, Rosin and Heinemann2008; Rosin et al.
Reference Rosin, Schekochihin, Rincon and Cowley2011; Kunz, Schekochihin & Stone Reference Kunz, Schekochihin and Stone2014a
; Hellinger et al.
Reference Hellinger, Matteini, Landi, Verdini, Franci and Trávníček2015; Rincon, Schekochihin & Cowley Reference Rincon, Schekochihin and Cowley2015; Riquelme, Quataert & Verscharen Reference Riquelme, Quataert and Verscharen2015; Sironi & Narayan Reference Sironi and Narayan2015; Melville, Schekochihin & Kunz Reference Melville, Schekochihin and Kunz2016; Riquelme, Quataert & Verscharen Reference Riquelme, Quataert and Verscharen2016), which have shown that these microinstabilities generally act to pin the pressure anisotropy at the marginal stability limits. Interestingly, when
![]() $\unicode[STIX]{x1D6E5}$
is driven beyond the stability boundaries, the microinstabilities achieve this in two stages: first, while the microscale fluctuations are growing secularly, by increasing (if
$\unicode[STIX]{x1D6E5}$
is driven beyond the stability boundaries, the microinstabilities achieve this in two stages: first, while the microscale fluctuations are growing secularly, by increasing (if
![]() $\text{d}_{t}B<0$
) or decreasing (if
$\text{d}_{t}B<0$
) or decreasing (if
![]() $\text{d}_{t}B>0$
) the magnetic-field strength
$\text{d}_{t}B>0$
) the magnetic-field strength
![]() $B$
(in other words, the small-scale fluctuations contribute to
$B$
(in other words, the small-scale fluctuations contribute to
![]() $B$
); second, as the instabilities saturate, by enhancing the scattering of particles and thus increasing
$B$
); second, as the instabilities saturate, by enhancing the scattering of particles and thus increasing
![]() $\unicode[STIX]{x1D708}_{c}$
in (2.4)–(2.5). While the time for the firehose instability at moderate
$\unicode[STIX]{x1D708}_{c}$
in (2.4)–(2.5). While the time for the firehose instability at moderate
![]() $\unicode[STIX]{x1D6FD}$
to saturate is essentially set by gyro-scale physics, and so might be considered as instantaneous in a fluid model, the mirror instability saturates on a time scales comparable to the turnover time of the large-scale motions driving the anisotropy (see § 6.3 and Kunz et al.
Reference Kunz, Schekochihin and Stone2014a
, Rincon et al.
Reference Rincon, Schekochihin and Cowley2015, Riquelme et al.
Reference Riquelme, Quataert and Verscharen2015, Melville et al.
Reference Melville, Schekochihin and Kunz2016). We also note that there are also various other kinetic instabilities that could be important, for instance, the ion-cyclotron instability, or electron instabilities. We do not consider these in detail because the mirror and firehose instabilities are thought to be the most relevant to the high-
$\unicode[STIX]{x1D6FD}$
to saturate is essentially set by gyro-scale physics, and so might be considered as instantaneous in a fluid model, the mirror instability saturates on a time scales comparable to the turnover time of the large-scale motions driving the anisotropy (see § 6.3 and Kunz et al.
Reference Kunz, Schekochihin and Stone2014a
, Rincon et al.
Reference Rincon, Schekochihin and Cowley2015, Riquelme et al.
Reference Riquelme, Quataert and Verscharen2015, Melville et al.
Reference Melville, Schekochihin and Kunz2016). We also note that there are also various other kinetic instabilities that could be important, for instance, the ion-cyclotron instability, or electron instabilities. We do not consider these in detail because the mirror and firehose instabilities are thought to be the most relevant to the high-
![]() $\unicode[STIX]{x1D6FD}$
, ion-dominated regime that is the focus of this work (see § 5 for further discussion).
$\unicode[STIX]{x1D6FD}$
, ion-dominated regime that is the focus of this work (see § 5 for further discussion).
In practice, because the primary effect in both the secular and scattering regimes is to limit
![]() $\unicode[STIX]{x1D6E5}$
at the threshold boundaries, we model these effects as a ‘hard-wall’ limit on
$\unicode[STIX]{x1D6E5}$
at the threshold boundaries, we model these effects as a ‘hard-wall’ limit on
![]() $\unicode[STIX]{x1D6E5}$
, following prior work (Reference Sharma, Hammett, Quataert and StoneS06; Sharma et al.
Reference Sharma, Quataert, Hammett and Stone2007, Santos-Lima et al.
Reference Santos-Lima, de Gouveia Dal Pino, Kowal, Falceta-Gonçalves, Lazarian and Nakwacki2014, Chandra et al.
Reference Chandra, Gammie, Foucart and Quataert2015, Foucart et al.
Reference Foucart, Chandra, Gammie and Quataert2015). This simply limits
$\unicode[STIX]{x1D6E5}$
, following prior work (Reference Sharma, Hammett, Quataert and StoneS06; Sharma et al.
Reference Sharma, Quataert, Hammett and Stone2007, Santos-Lima et al.
Reference Santos-Lima, de Gouveia Dal Pino, Kowal, Falceta-Gonçalves, Lazarian and Nakwacki2014, Chandra et al.
Reference Chandra, Gammie, Foucart and Quataert2015, Foucart et al.
Reference Foucart, Chandra, Gammie and Quataert2015). This simply limits
![]() $\unicode[STIX]{x1D6E5}$
to
$\unicode[STIX]{x1D6E5}$
to
![]() $1/\unicode[STIX]{x1D6FD}$
or
$1/\unicode[STIX]{x1D6FD}$
or
![]() $-2/\unicode[STIX]{x1D6FD}$
if the dynamics drives
$-2/\unicode[STIX]{x1D6FD}$
if the dynamics drives
![]() $\unicode[STIX]{x1D6E5}$
across these boundaries.Footnote
3
One should, however, be careful with this simple ‘limiter’ method not to inadvertently remove interesting physics from the model. For instance, the parallel firehose instability is destabilized at the same point
$\unicode[STIX]{x1D6E5}$
across these boundaries.Footnote
3
One should, however, be careful with this simple ‘limiter’ method not to inadvertently remove interesting physics from the model. For instance, the parallel firehose instability is destabilized at the same point
![]() $\unicode[STIX]{x1D6E5}=-2/\unicode[STIX]{x1D6FD}$
as where the magnetic tension is nullified by
$\unicode[STIX]{x1D6E5}=-2/\unicode[STIX]{x1D6FD}$
as where the magnetic tension is nullified by
![]() $\unicode[STIX]{x0394}p$
(indeed, this is the cause of the instability), which can have a strong influence on the largest scales (Squire, Quataert & Schekochihin Reference Squire, Quataert and Schekochihin2016; Squire et al.
Reference Squire, Schekochihin and Quataert2017) and is captured in even our simplest 1-D models. For this reason, in considering azimuthal-field KMRI modes, we have run calculations both with and without a firehose limiter, seeing very similar dynamics in each case. Finally, we note that with finite scale separations between
$\unicode[STIX]{x0394}p$
(indeed, this is the cause of the instability), which can have a strong influence on the largest scales (Squire, Quataert & Schekochihin Reference Squire, Quataert and Schekochihin2016; Squire et al.
Reference Squire, Schekochihin and Quataert2017) and is captured in even our simplest 1-D models. For this reason, in considering azimuthal-field KMRI modes, we have run calculations both with and without a firehose limiter, seeing very similar dynamics in each case. Finally, we note that with finite scale separations between
![]() $\unicode[STIX]{x1D6FA}_{i}$
and
$\unicode[STIX]{x1D6FA}_{i}$
and
![]() $S$
, as is the case in numerical simulations (Riquelme et al.
Reference Riquelme, Quataert, Sharma and Spitkovsky2012; Hoshino Reference Hoshino2015; Kunz et al.
Reference Kunz, Stone and Quataert2016), there can be significant overshoot of the pressure anisotropy beyond the limits (2.9) and (2.10) (Kunz et al.
Reference Kunz, Schekochihin and Stone2014a
). This overshoot may be important for the large-scale evolution (see § 3) but is probably not representative of what happens in real systems, which usually have a very large dynamic range between
$S$
, as is the case in numerical simulations (Riquelme et al.
Reference Riquelme, Quataert, Sharma and Spitkovsky2012; Hoshino Reference Hoshino2015; Kunz et al.
Reference Kunz, Stone and Quataert2016), there can be significant overshoot of the pressure anisotropy beyond the limits (2.9) and (2.10) (Kunz et al.
Reference Kunz, Schekochihin and Stone2014a
). This overshoot may be important for the large-scale evolution (see § 3) but is probably not representative of what happens in real systems, which usually have a very large dynamic range between
![]() $\unicode[STIX]{x1D6FA}_{i}$
and
$\unicode[STIX]{x1D6FA}_{i}$
and
![]() $S$
. These effects are discussed in detail in § 6.
$S$
. These effects are discussed in detail in § 6.
2.2 Computational methods
A number of different numerical methods are used to solve (2.1)–(2.7). For investigating the 1-D evolution of a channel mode, we use a pseudo-spectral method, with standard dealiasing and hyper-diffusion operators used to remove the energy just above the grid scale. A very similar numerical method, albeit on a 3-D Fourier grid, is used for the studies of parasitic modes. For studies of the fully nonlinear 3-D evolution, we use a modified version of the finite-difference code Zeus, as described in Reference Sharma, Hammett, Quataert and StoneS06. For simulations in the weakly collisional regime, we solve the full LF system (2.1)–(2.7), so as to correctly capture the effects of the heat fluxes in the moderate- and high-collisionality regimes (see § B.4).
A few words are needed regarding the numerical treatment of heat fluxes in the LF model (2.6)–(2.7). In particular, the
![]() $1/|k_{\Vert }|$
operator is numerically awkward, because it is not diagonal in either Fourier space or real space. We thus use the prescription of Reference Sharma, Hammett, Quataert and StoneS06 and replace this by a pre-chosen
$1/|k_{\Vert }|$
operator is numerically awkward, because it is not diagonal in either Fourier space or real space. We thus use the prescription of Reference Sharma, Hammett, Quataert and StoneS06 and replace this by a pre-chosen
![]() $k_{L}$
for the Zeus implementation and the parasitic-mode studies, while for the 1-D collisionless calculations we use
$k_{L}$
for the Zeus implementation and the parasitic-mode studies, while for the 1-D collisionless calculations we use
![]() $1/|k_{\Vert }|=1/|k_{z}|$
(once the mode reaches larger amplitude this may somewhat underestimate the heat fluxes, since
$1/|k_{\Vert }|=1/|k_{z}|$
(once the mode reaches larger amplitude this may somewhat underestimate the heat fluxes, since
![]() $k_{\Vert }<k_{z}$
if the field lines are not straight). Following Reference Sharma, Hammett, Quataert and StoneS06, we have checked that varying the choice of
$k_{\Vert }<k_{z}$
if the field lines are not straight). Following Reference Sharma, Hammett, Quataert and StoneS06, we have checked that varying the choice of
![]() $k_{L}$
within a reasonable range, or using the choice
$k_{L}$
within a reasonable range, or using the choice
![]() $|k_{\Vert }|=|k_{z}|$
, does not significantly affect the dynamics.
$|k_{\Vert }|=|k_{z}|$
, does not significantly affect the dynamics.
We use the methods detailed in appendix A3 of Reference Sharma, Hammett, Quataert and StoneS06 to limit the pressure anisotropy:
![]() $\unicode[STIX]{x1D708}_{c}$
is instantaneously increased in (2.4)–(2.5) whenever
$\unicode[STIX]{x1D708}_{c}$
is instantaneously increased in (2.4)–(2.5) whenever
![]() $\unicode[STIX]{x1D6E5}$
passes the limits (2.9) or (2.10). We do not make any distinction between the ‘secular growth’ and ‘particle scattering’ phases of microinstability evolution with this method (see discussion above, around (2.10), and § 6.3), and more study is needed to better understand the successes and limitations of this simple limiter approach.
$\unicode[STIX]{x1D6E5}$
passes the limits (2.9) or (2.10). We do not make any distinction between the ‘secular growth’ and ‘particle scattering’ phases of microinstability evolution with this method (see discussion above, around (2.10), and § 6.3), and more study is needed to better understand the successes and limitations of this simple limiter approach.
2.3 General comparison of kinetic models
Before commencing with our analysis of the KMRI, we highlight in this section some of the key similarities and differences between the LF, Braginskii and CGL models, as well as that of standard MHD.
First, irrespective of the closure details, the general effect of pressure anisotropy is to modify the Lorentz force, either by enhancing (
![]() $\unicode[STIX]{x0394}p>0$
) or reducing (
$\unicode[STIX]{x0394}p>0$
) or reducing (
![]() $\unicode[STIX]{x0394}p<0$
) the effective magnetic tension (see (2.2)). The same relative pressure anisotropy
$\unicode[STIX]{x0394}p<0$
) the effective magnetic tension (see (2.2)). The same relative pressure anisotropy
![]() $\unicode[STIX]{x1D6E5}=\unicode[STIX]{x0394}p/p_{0}$
will thus have a greater dynamical effect as
$\unicode[STIX]{x1D6E5}=\unicode[STIX]{x0394}p/p_{0}$
will thus have a greater dynamical effect as
![]() $\unicode[STIX]{x1D6FD}$
increases, because
$\unicode[STIX]{x1D6FD}$
increases, because
![]() $p_{0}$
increases compared to
$p_{0}$
increases compared to
![]() $B$
. In contrast, the generation of
$B$
. In contrast, the generation of
![]() $\unicode[STIX]{x1D6E5}$
in a changing magnetic field,
$\unicode[STIX]{x1D6E5}$
in a changing magnetic field,
(or
![]() $\unicode[STIX]{x1D6E5}\sim \unicode[STIX]{x1D708}_{c}^{-1}\hat{\boldsymbol{b}}\hat{\boldsymbol{b}}\,\boldsymbol{ : }\,\unicode[STIX]{x1D735}\boldsymbol{u}$
for Braginskii), does not depend on
$\unicode[STIX]{x1D6E5}\sim \unicode[STIX]{x1D708}_{c}^{-1}\hat{\boldsymbol{b}}\hat{\boldsymbol{b}}\,\boldsymbol{ : }\,\unicode[STIX]{x1D735}\boldsymbol{u}$
for Braginskii), does not depend on
![]() $\unicode[STIX]{x1D6FD}$
. Thus, the dynamics of higher-
$\unicode[STIX]{x1D6FD}$
. Thus, the dynamics of higher-
![]() $\unicode[STIX]{x1D6FD}$
plasmas is in general more strongly influenced by self-generated pressure anisotropies than is the dynamics of lower-
$\unicode[STIX]{x1D6FD}$
plasmas is in general more strongly influenced by self-generated pressure anisotropies than is the dynamics of lower-
![]() $\unicode[STIX]{x1D6FD}$
plasmas.
$\unicode[STIX]{x1D6FD}$
plasmas.
Secondly, the spatial form of
![]() $\unicode[STIX]{x0394}p$
generated in a given time-dependent
$\unicode[STIX]{x0394}p$
generated in a given time-dependent
![]() $B$
differs significantly between the LF, CGL and Braginskii models. This
$B$
differs significantly between the LF, CGL and Braginskii models. This
![]() $\unicode[STIX]{x0394}p$
is important for the nonlinear behaviour of the collisionless MRI. The influence of a spatially constant
$\unicode[STIX]{x0394}p$
is important for the nonlinear behaviour of the collisionless MRI. The influence of a spatially constant
![]() $\unicode[STIX]{x1D6E5}$
can be considered from an essentially linear standpoint: it simply acts to enhance or reduce the Lorentz force by the factor
$\unicode[STIX]{x1D6E5}$
can be considered from an essentially linear standpoint: it simply acts to enhance or reduce the Lorentz force by the factor
![]() $(1+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}/2)$
. In contrast, when the spatial variation in
$(1+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}/2)$
. In contrast, when the spatial variation in
![]() $\unicode[STIX]{x1D6E5}$
is similar to its magnitude, its effect is inherently nonlinear. For the same reason, detailed conclusions about the expected change in the spatial shape of an MRI mode due to pressure anisotropy do depend on the regime of interest (and model) – for example, collisionless versus Braginskii (Squire et al.
Reference Squire, Quataert and Schekochihin2016), or low versus high
$\unicode[STIX]{x1D6E5}$
is similar to its magnitude, its effect is inherently nonlinear. For the same reason, detailed conclusions about the expected change in the spatial shape of an MRI mode due to pressure anisotropy do depend on the regime of interest (and model) – for example, collisionless versus Braginskii (Squire et al.
Reference Squire, Quataert and Schekochihin2016), or low versus high
![]() $\unicode[STIX]{x1D6FD}$
– rather than being generic consequences of any self-generated pressure anisotropy. For our purposes, one can consider high-collisionality Braginskii MHD (equation (2.8)) as the limiting model that develops large spatial variation in
$\unicode[STIX]{x1D6FD}$
– rather than being generic consequences of any self-generated pressure anisotropy. For our purposes, one can consider high-collisionality Braginskii MHD (equation (2.8)) as the limiting model that develops large spatial variation in
![]() $\unicode[STIX]{x1D6E5}$
(since
$\unicode[STIX]{x1D6E5}$
(since
![]() $\unicode[STIX]{x1D6E5}$
is tied directly to
$\unicode[STIX]{x1D6E5}$
is tied directly to
![]() $\text{d}_{t}B$
), while the high-
$\text{d}_{t}B$
), while the high-
![]() $\unicode[STIX]{x1D6FD}$
limit of the LF model is the opposite, developing large
$\unicode[STIX]{x1D6FD}$
limit of the LF model is the opposite, developing large
![]() $\unicode[STIX]{x1D6E5}$
with very little spatial variation.Footnote
4
This is because collisions generically act to reduce the magnitude of
$\unicode[STIX]{x1D6E5}$
with very little spatial variation.Footnote
4
This is because collisions generically act to reduce the magnitude of
![]() $\unicode[STIX]{x1D6E5}$
without affecting the spatial variation in
$\unicode[STIX]{x1D6E5}$
without affecting the spatial variation in
![]() $p_{\bot }$
and
$p_{\bot }$
and
![]() $p_{\Vert }$
, whereas heat fluxes act to reduce spatial variation in
$p_{\Vert }$
, whereas heat fluxes act to reduce spatial variation in
![]() $p_{\bot }$
and
$p_{\bot }$
and
![]() $p_{\Vert }$
without affecting the spatial average of
$p_{\Vert }$
without affecting the spatial average of
![]() $\unicode[STIX]{x1D6E5}$
.
$\unicode[STIX]{x1D6E5}$
.
This last statement warrants further explanation, given the complexity of (2.4)–(2.7). The effect of the LF heat fluxes (2.6)–(2.7) can be clarified if we assume
![]() $\unicode[STIX]{x1D708}_{c}=0$
and
$\unicode[STIX]{x1D708}_{c}=0$
and
![]() $\unicode[STIX]{x0394}p\ll p_{0}$
(the latter is always valid at high
$\unicode[STIX]{x0394}p\ll p_{0}$
(the latter is always valid at high
![]() $\unicode[STIX]{x1D6FD}$
), so that
$\unicode[STIX]{x1D6FD}$
), so that
Then, assuming
![]() $\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}q_{\bot ,\Vert }\gg q_{\bot ,\Vert }\unicode[STIX]{x1D735}\boldsymbol{\cdot }\hat{\boldsymbol{b}}$
, which is valid when the perturbation to the background field is small (i.e. when the field lines are nearly straight), the contribution to the
$\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}q_{\bot ,\Vert }\gg q_{\bot ,\Vert }\unicode[STIX]{x1D735}\boldsymbol{\cdot }\hat{\boldsymbol{b}}$
, which is valid when the perturbation to the background field is small (i.e. when the field lines are nearly straight), the contribution to the
![]() $p_{\bot }$
and
$p_{\bot }$
and
![]() $p_{\Vert }$
evolution equations has the form
$p_{\Vert }$
evolution equations has the form
![]() $\unicode[STIX]{x2202}_{t}p_{\bot }\sim -\unicode[STIX]{x1D70C}c_{s}|k_{\Vert }|(p_{\bot }/\unicode[STIX]{x1D70C})$
and
$\unicode[STIX]{x2202}_{t}p_{\bot }\sim -\unicode[STIX]{x1D70C}c_{s}|k_{\Vert }|(p_{\bot }/\unicode[STIX]{x1D70C})$
and
![]() $\unicode[STIX]{x2202}_{t}p_{\Vert }\sim -\unicode[STIX]{x1D70C}c_{s}|k_{\Vert }|(p_{\Vert }/\unicode[STIX]{x1D70C})$
, respectively. These terms, which model the effect of Landau damping (Snyder et al.
Reference Snyder, Hammett and Dorland1997), act as a ‘scale-independent’ diffusion of
$\unicode[STIX]{x2202}_{t}p_{\Vert }\sim -\unicode[STIX]{x1D70C}c_{s}|k_{\Vert }|(p_{\Vert }/\unicode[STIX]{x1D70C})$
, respectively. These terms, which model the effect of Landau damping (Snyder et al.
Reference Snyder, Hammett and Dorland1997), act as a ‘scale-independent’ diffusion of
![]() $p_{\bot }$
and
$p_{\bot }$
and
![]() $p_{\Vert }$
, damping inhomogeneitiesFootnote
5
over the sound-wave time scale
$p_{\Vert }$
, damping inhomogeneitiesFootnote
5
over the sound-wave time scale
![]() $|k_{\Vert }|c_{s}$
. This is important because
$|k_{\Vert }|c_{s}$
. This is important because
![]() $|k_{\Vert }|c_{s}\sim \unicode[STIX]{x1D6FD}^{1/2}\unicode[STIX]{x1D6FE}_{\text{MRI}}$
(where
$|k_{\Vert }|c_{s}\sim \unicode[STIX]{x1D6FD}^{1/2}\unicode[STIX]{x1D6FE}_{\text{MRI}}$
(where
![]() $\unicode[STIX]{x1D6FE}_{\text{MRI}}$
is the MRI growth rate), showing that for
$\unicode[STIX]{x1D6FE}_{\text{MRI}}$
is the MRI growth rate), showing that for
![]() $\unicode[STIX]{x1D6FD}\gg 1$
, the heat fluxes will rapidly erase spatial variation in
$\unicode[STIX]{x1D6FD}\gg 1$
, the heat fluxes will rapidly erase spatial variation in
![]() $\unicode[STIX]{x0394}p$
on the time scale that the MRI grows. As a result, the spatial variation in
$\unicode[STIX]{x0394}p$
on the time scale that the MRI grows. As a result, the spatial variation in
![]() $\unicode[STIX]{x0394}p$
will be dwarfed by its mean; i.e.
$\unicode[STIX]{x0394}p$
will be dwarfed by its mean; i.e.
![]() $\unicode[STIX]{x0394}p$
will be nearly spatially constant. A more thorough discussion of these ideas is given in appendix B, where we solve explicitly for the
$\unicode[STIX]{x0394}p$
will be nearly spatially constant. A more thorough discussion of these ideas is given in appendix B, where we solve explicitly for the
![]() $\unicode[STIX]{x0394}p$
that arises in an exponentially growing, spatially varying magnetic perturbation. This shows that the double-adiabatic model for
$\unicode[STIX]{x0394}p$
that arises in an exponentially growing, spatially varying magnetic perturbation. This shows that the double-adiabatic model for
![]() $p_{\bot ,\Vert }$
generates a
$p_{\bot ,\Vert }$
generates a
![]() $\unicode[STIX]{x0394}p$
with spatial variation of the order of its mean, while the addition of LF heat fluxes decreases the spatial variation of
$\unicode[STIX]{x0394}p$
with spatial variation of the order of its mean, while the addition of LF heat fluxes decreases the spatial variation of
![]() $\unicode[STIX]{x0394}p$
by a factor
$\unicode[STIX]{x0394}p$
by a factor
![]() $\unicode[STIX]{x1D6FD}^{1/2}$
while leaving the mean
$\unicode[STIX]{x1D6FD}^{1/2}$
while leaving the mean
![]() $\unicode[STIX]{x0394}p$
unchanged.
$\unicode[STIX]{x0394}p$
unchanged.
3 One-dimensional evolution
In this section, we discuss various nonlinear effects that occur due to the pressure anisotropy that develops in a growing KMRI mode. These effects are one-dimensional (i.e. unrelated to ‘parasitic’ modes and turbulence, which is discussed in § 4) and occur at very low mode amplitudes: when
![]() $\unicode[STIX]{x1D6FF}B\sim \unicode[STIX]{x1D6FD}^{-1/2}B_{0}$
in a purely vertical field, or when
$\unicode[STIX]{x1D6FF}B\sim \unicode[STIX]{x1D6FD}^{-1/2}B_{0}$
in a purely vertical field, or when
![]() $\unicode[STIX]{x1D6FF}B_{y}\sim \unicode[STIX]{x1D6FD}^{-2/3}B_{0}$
and
$\unicode[STIX]{x1D6FF}B_{y}\sim \unicode[STIX]{x1D6FD}^{-2/3}B_{0}$
and
![]() $\unicode[STIX]{x1D6FF}B_{x}\sim \unicode[STIX]{x1D6FD}^{-1/3}B_{0}$
with an azimuthal field (where
$\unicode[STIX]{x1D6FF}B_{x}\sim \unicode[STIX]{x1D6FD}^{-1/3}B_{0}$
with an azimuthal field (where
![]() $\unicode[STIX]{x1D6FF}B$
denotes the mode amplitude). This provides an interesting counterpoint to MHD MRI channel modes, which are nonlinear solutions of the incompressible MHD equations (Goodman & Xu Reference Goodman and Xu1994), and only exhibit notable nonlinear modifications as the mode amplitude approaches the sound speed,
$\unicode[STIX]{x1D6FF}B$
denotes the mode amplitude). This provides an interesting counterpoint to MHD MRI channel modes, which are nonlinear solutions of the incompressible MHD equations (Goodman & Xu Reference Goodman and Xu1994), and only exhibit notable nonlinear modifications as the mode amplitude approaches the sound speed,
![]() $\unicode[STIX]{x1D6FF}B\sim \unicode[STIX]{x1D6FD}^{1/2}B_{0}$
. However, we will also see that despite this early (low-amplitude) nonlinear modification, once a KMRI mode’s amplitude starts to dominate over the background field (
$\unicode[STIX]{x1D6FF}B\sim \unicode[STIX]{x1D6FD}^{1/2}B_{0}$
. However, we will also see that despite this early (low-amplitude) nonlinear modification, once a KMRI mode’s amplitude starts to dominate over the background field (
![]() $\unicode[STIX]{x1D6FF}B\gtrsim B_{0}$
), it reverts to being an approximate nonlinear solution, because of the pressure-anisotropy-limiting behaviour of the mirror instability. Thus a KMRI mode behaves very similarly to an MHD channel mode as
$\unicode[STIX]{x1D6FF}B\gtrsim B_{0}$
), it reverts to being an approximate nonlinear solution, because of the pressure-anisotropy-limiting behaviour of the mirror instability. Thus a KMRI mode behaves very similarly to an MHD channel mode as
![]() $\unicode[STIX]{x1D6FF}B$
approaches
$\unicode[STIX]{x1D6FF}B$
approaches
![]() $\unicode[STIX]{x1D6FD}^{1/2}B_{0}$
.
$\unicode[STIX]{x1D6FD}^{1/2}B_{0}$
.
We begin by outlining the basic linear physics of the KMRI (§ 3.1), which will be relevant to its nonlinear evolution. We then examine various stages in the evolution of a 1-D collisionless KMRI mode in vertical (§ 3.2) or mixed-azimuthal–vertical (§ 3.3) background magnetic fields, before the mode saturates into turbulence. We also discuss how these stages are modified in the weakly collisional (Braginskii) regime (§§ 3.2.2, 3.3.2). Throughout this section we denote the MRI perturbation velocity and magnetic field as
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{u}$
and
$\unicode[STIX]{x1D6FF}\boldsymbol{u}$
and
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{B}$
respectively (their magnitudes are
$\unicode[STIX]{x1D6FF}\boldsymbol{B}$
respectively (their magnitudes are
![]() $\unicode[STIX]{x1D6FF}u$
and
$\unicode[STIX]{x1D6FF}u$
and
![]() $\unicode[STIX]{x1D6FF}B$
), the background magnetic field as
$\unicode[STIX]{x1D6FF}B$
), the background magnetic field as
![]() $\boldsymbol{B}_{0}=B_{0y}\hat{\boldsymbol{y}}+B_{0z}\hat{\boldsymbol{z}}$
, and
$\boldsymbol{B}_{0}=B_{0y}\hat{\boldsymbol{y}}+B_{0z}\hat{\boldsymbol{z}}$
, and
![]() $\unicode[STIX]{x1D6FD}_{0}=8\unicode[STIX]{x03C0}p_{0}/B_{0}^{2}$
is defined with respect to the background field (we also use
$\unicode[STIX]{x1D6FD}_{0}=8\unicode[STIX]{x03C0}p_{0}/B_{0}^{2}$
is defined with respect to the background field (we also use
![]() $\unicode[STIX]{x1D6FD}_{0z}=8\unicode[STIX]{x03C0}p_{0}/B_{0z}^{2}$
). For the reader interested in a general overview of results, the summary in § 3.4 should be understandable without a careful reading of §§ 3.1–3.3.
$\unicode[STIX]{x1D6FD}_{0z}=8\unicode[STIX]{x03C0}p_{0}/B_{0z}^{2}$
). For the reader interested in a general overview of results, the summary in § 3.4 should be understandable without a careful reading of §§ 3.1–3.3.
3.1 Linear KMRI
Before discussing any nonlinear effects, it is helpful to first review aspects of the linear KMRI. We consider only the simplest case of purely vertical wavenumbers
![]() $k_{z}\neq 0$
,
$k_{z}\neq 0$
,
![]() $k_{x}=k_{y}=0$
; i.e.
$k_{x}=k_{y}=0$
; i.e.
![]() $(\boldsymbol{k}\Vert \boldsymbol{B}\Vert \unicode[STIX]{x1D734})$
. This choice is motivated by the stabilizing influence of a non-zero radial wavenumber
$(\boldsymbol{k}\Vert \boldsymbol{B}\Vert \unicode[STIX]{x1D734})$
. This choice is motivated by the stabilizing influence of a non-zero radial wavenumber
![]() $k_{x}$
(see discussion in § 4 of Reference Quataert, Dorland and HammettQ02), meaning that
$k_{x}$
(see discussion in § 4 of Reference Quataert, Dorland and HammettQ02), meaning that
![]() $k_{x}=0$
modes should dominate if growing from small amplitudes, while treating
$k_{x}=0$
modes should dominate if growing from small amplitudes, while treating
![]() $k_{y}\neq 0$
modes requires a global and/or time-dependent method (Balbus & Hawley Reference Balbus and Hawley1992; Johnson Reference Johnson2007; Squire & Bhattacharjee Reference Squire and Bhattacharjee2014a
). We also neglect the possibility of a radial background magnetic field since this leads to a time-dependent background azimuthal field. More thorough discussion and detailed derivations can be found in Reference Quataert, Dorland and HammettQ02; Sharma et al. (Reference Sharma, Hammett and Quataert2003), Balbus (Reference Balbus2004), Rosin & Mestel (Reference Rosin and Mestel2012), Heinemann & Quataert (Reference Heinemann and Quataert2014), Quataert et al. (Reference Quataert, Heinemann and Spitkovsky2015), as well in appendix A, where we derive properties of the KMRI in a mixed-vertical–azimuthal field.
$k_{y}\neq 0$
modes requires a global and/or time-dependent method (Balbus & Hawley Reference Balbus and Hawley1992; Johnson Reference Johnson2007; Squire & Bhattacharjee Reference Squire and Bhattacharjee2014a
). We also neglect the possibility of a radial background magnetic field since this leads to a time-dependent background azimuthal field. More thorough discussion and detailed derivations can be found in Reference Quataert, Dorland and HammettQ02; Sharma et al. (Reference Sharma, Hammett and Quataert2003), Balbus (Reference Balbus2004), Rosin & Mestel (Reference Rosin and Mestel2012), Heinemann & Quataert (Reference Heinemann and Quataert2014), Quataert et al. (Reference Quataert, Heinemann and Spitkovsky2015), as well in appendix A, where we derive properties of the KMRI in a mixed-vertical–azimuthal field.
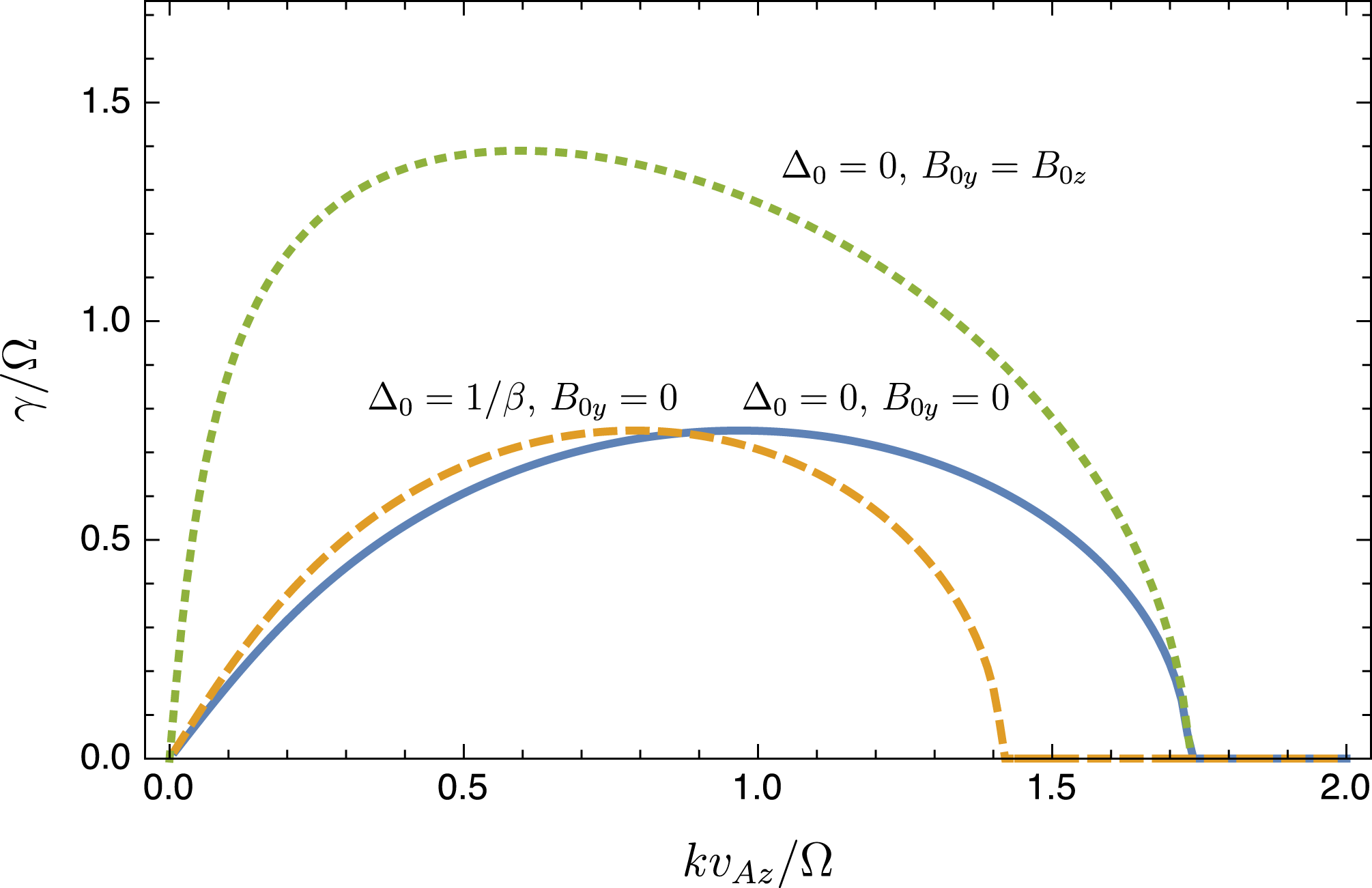
Figure 1. Dimensionless linear growth rate
![]() $\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D6FA}$
of the KMRI at
$\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D6FA}$
of the KMRI at
![]() $\unicode[STIX]{x1D6FD}_{0z}=8\unicode[STIX]{x03C0}p_{0}/B_{0z}^{2}=400$
and
$\unicode[STIX]{x1D6FD}_{0z}=8\unicode[STIX]{x03C0}p_{0}/B_{0z}^{2}=400$
and
![]() $S/\unicode[STIX]{x1D6FA}=3/2$
, plotted as a function of dimensionless vertical wavenumber
$S/\unicode[STIX]{x1D6FA}=3/2$
, plotted as a function of dimensionless vertical wavenumber
![]() $k_{z}v_{Az}/\unicode[STIX]{x1D6FA}$
(with
$k_{z}v_{Az}/\unicode[STIX]{x1D6FA}$
(with
![]() $k_{x}=k_{y}=0$
). The solid blue curve shows the case with a purely vertical
$k_{x}=k_{y}=0$
). The solid blue curve shows the case with a purely vertical
![]() $\boldsymbol{B}_{0}$
and no background pressure anisotropy
$\boldsymbol{B}_{0}$
and no background pressure anisotropy
![]() $\unicode[STIX]{x1D6E5}_{0}$
, for which the dispersion relation is identical to the standard MRI. The orange dashed line shows the case with
$\unicode[STIX]{x1D6E5}_{0}$
, for which the dispersion relation is identical to the standard MRI. The orange dashed line shows the case with
![]() $B_{0y}=0$
and
$B_{0y}=0$
and
![]() $\unicode[STIX]{x1D6E5}_{0}=1/\unicode[STIX]{x1D6FD}_{0}$
, which is approximately the anisotropy at which the mirror limit is first reached in the growing mode. Finally, the green dotted line shows the growth rate in the case with an azimuthal field
$\unicode[STIX]{x1D6E5}_{0}=1/\unicode[STIX]{x1D6FD}_{0}$
, which is approximately the anisotropy at which the mirror limit is first reached in the growing mode. Finally, the green dotted line shows the growth rate in the case with an azimuthal field
![]() $B_{0y}=B_{0z}$
(with
$B_{0y}=B_{0z}$
(with
![]() $\unicode[STIX]{x1D6FD}_{0z}=400$
,
$\unicode[STIX]{x1D6FD}_{0z}=400$
,
![]() $\unicode[STIX]{x1D6FD}_{0}=200$
), where the growth rate is strongly enhanced compared to the MHD MRI (which is unaffected by the azimuthal field for
$\unicode[STIX]{x1D6FD}_{0}=200$
), where the growth rate is strongly enhanced compared to the MHD MRI (which is unaffected by the azimuthal field for
![]() $k_{x}=k_{y}=0$
).
$k_{x}=k_{y}=0$
).
We linearize (2.1)–(2.7) with
![]() $\unicode[STIX]{x1D708}_{c}=0$
and
$\unicode[STIX]{x1D708}_{c}=0$
and
![]() $S/\unicode[STIX]{x1D6FA}=3/2$
, then insert the Fourier ansatz
$S/\unicode[STIX]{x1D6FA}=3/2$
, then insert the Fourier ansatz
![]() $\unicode[STIX]{x1D6FF}f(z,t)=\unicode[STIX]{x1D6FF}f\text{e}^{\text{i}kz-\text{i}\unicode[STIX]{x1D714}t}$
for each variable (
$\unicode[STIX]{x1D6FF}f(z,t)=\unicode[STIX]{x1D6FF}f\text{e}^{\text{i}kz-\text{i}\unicode[STIX]{x1D714}t}$
for each variable (
![]() $f=\unicode[STIX]{x1D70C}$
,
$f=\unicode[STIX]{x1D70C}$
,
![]() $\boldsymbol{u}$
,
$\boldsymbol{u}$
,
![]() $\boldsymbol{B}$
etc.). Solution of the resulting polynomial equation for
$\boldsymbol{B}$
etc.). Solution of the resulting polynomial equation for
![]() $\unicode[STIX]{x1D714}$
yields the linear KMRI growth rates,
$\unicode[STIX]{x1D714}$
yields the linear KMRI growth rates,
![]() $\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D6FA}=\text{Im}(\unicode[STIX]{x1D714})/\unicode[STIX]{x1D6FA}$
, as shown in figure 1 for several relevant cases. For the case of purely vertical field and no background pressure anisotropy (solid line), the KMRI dispersion relation is identical to the collisional MRI. This occurs because when
$\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D6FA}=\text{Im}(\unicode[STIX]{x1D714})/\unicode[STIX]{x1D6FA}$
, as shown in figure 1 for several relevant cases. For the case of purely vertical field and no background pressure anisotropy (solid line), the KMRI dispersion relation is identical to the collisional MRI. This occurs because when
![]() $\boldsymbol{B}_{0}=B_{0}\hat{\boldsymbol{z}}$
the MRI does not linearly perturb the pressure (because
$\boldsymbol{B}_{0}=B_{0}\hat{\boldsymbol{z}}$
the MRI does not linearly perturb the pressure (because
![]() $\unicode[STIX]{x2202}_{z}(\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D6FF}\boldsymbol{B})=0$
), and thus is ignorant of the equation of state. With a non-zero radial wavenumber
$\unicode[STIX]{x2202}_{z}(\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D6FF}\boldsymbol{B})=0$
), and thus is ignorant of the equation of state. With a non-zero radial wavenumber
![]() $k_{x}\neq 0$
, this is no longer the case (since then
$k_{x}\neq 0$
, this is no longer the case (since then
![]() $\unicode[STIX]{x1D6FF}B_{z}\neq 0$
), and the growth rate is lower than for the standard MRI.
$\unicode[STIX]{x1D6FF}B_{z}\neq 0$
), and the growth rate is lower than for the standard MRI.
The addition of a background positive pressure anisotropy,
![]() $\unicode[STIX]{x1D6E5}_{0}>0$
, shifts the MRI to larger wavelengths (smaller
$\unicode[STIX]{x1D6E5}_{0}>0$
, shifts the MRI to larger wavelengths (smaller
![]() $k$
; dashed curve in figure 1). This is because the anisotropic-pressure stress in the momentum equation has a form identical to that of the Lorentz force (see (2.2)). Thus the only difference in comparison to the standard MRI dispersion relation is the replacement of
$k$
; dashed curve in figure 1). This is because the anisotropic-pressure stress in the momentum equation has a form identical to that of the Lorentz force (see (2.2)). Thus the only difference in comparison to the standard MRI dispersion relation is the replacement of
![]() $kv_{A}$
with
$kv_{A}$
with
![]() $kv_{A}(1+\unicode[STIX]{x1D6FD}_{0}\unicode[STIX]{x1D6E5}_{0}/2)^{1/2}$
, which decreases the wavenumber that maximizes
$kv_{A}(1+\unicode[STIX]{x1D6FD}_{0}\unicode[STIX]{x1D6E5}_{0}/2)^{1/2}$
, which decreases the wavenumber that maximizes
![]() $\unicode[STIX]{x1D6FE}$
from
$\unicode[STIX]{x1D6FE}$
from
![]() ${\sim}\!\unicode[STIX]{x1D6FA}v_{A}^{-1}$
to
${\sim}\!\unicode[STIX]{x1D6FA}v_{A}^{-1}$
to
![]() ${\sim}\!\unicode[STIX]{x1D6FA}v_{A}^{-1}(1+\unicode[STIX]{x1D6FD}_{0}\unicode[STIX]{x1D6E5}_{0}/2)^{-1/2}$
, while keeping the maximum itself constant. This is relevant to the nonlinear behaviour of the KMRI, since the mode generates a pressure anisotropy as it evolves.
${\sim}\!\unicode[STIX]{x1D6FA}v_{A}^{-1}(1+\unicode[STIX]{x1D6FD}_{0}\unicode[STIX]{x1D6E5}_{0}/2)^{-1/2}$
, while keeping the maximum itself constant. This is relevant to the nonlinear behaviour of the KMRI, since the mode generates a pressure anisotropy as it evolves.
Finally, the addition of a background azimuthal field causes the KMRI dispersion relation to differ significantly from that of the standard MRI (Reference Quataert, Dorland and HammettQ02; Balbus Reference Balbus2004; dotted curve in figure 1), increasing the growth rate and moving the instability to larger wavelengths. This differs from the standard (MHD) MRI, which is unaffected by
![]() $B_{0y}\neq 0$
when
$B_{0y}\neq 0$
when
![]() $k_{y}=0$
. Due to the different physical processes that lead to the large growth rates at low
$k_{y}=0$
. Due to the different physical processes that lead to the large growth rates at low
![]() $k$
, this instability is also known as the magnetoviscous instability (MVI; Balbus Reference Balbus2004). Unlike the standard MRI, the growth mechanism relies on the azimuthal pressure force
$k$
, this instability is also known as the magnetoviscous instability (MVI; Balbus Reference Balbus2004). Unlike the standard MRI, the growth mechanism relies on the azimuthal pressure force
![]() $\hat{\boldsymbol{b}}_{0}\hat{\boldsymbol{b}}_{0}\unicode[STIX]{x1D6FF}\unicode[STIX]{x0394}p$
, which is destabilizing and dominates over the magnetic tension by a factor of
$\hat{\boldsymbol{b}}_{0}\hat{\boldsymbol{b}}_{0}\unicode[STIX]{x1D6FF}\unicode[STIX]{x0394}p$
, which is destabilizing and dominates over the magnetic tension by a factor of
![]() $\unicode[STIX]{x1D6FD}_{0}^{1/2}$
(see Reference Quataert, Dorland and HammettQ02). As shown in appendix A, for
$\unicode[STIX]{x1D6FD}_{0}^{1/2}$
(see Reference Quataert, Dorland and HammettQ02). As shown in appendix A, for
![]() $\unicode[STIX]{x1D6FD}_{0}\gg 1$
the KMRI growth rate approaches
$\unicode[STIX]{x1D6FD}_{0}\gg 1$
the KMRI growth rate approaches
![]() $\unicode[STIX]{x1D6FE}=(2S\unicode[STIX]{x1D6FA})^{1/2}$
, with a maximum growth rate at wavenumber
$\unicode[STIX]{x1D6FE}=(2S\unicode[STIX]{x1D6FA})^{1/2}$
, with a maximum growth rate at wavenumber
![]() $k_{\text{max}}v_{Az}/\unicode[STIX]{x1D6FA}\approx 1.8\,\unicode[STIX]{x1D6FD}_{0z}^{-1/6}$
when
$k_{\text{max}}v_{Az}/\unicode[STIX]{x1D6FA}\approx 1.8\,\unicode[STIX]{x1D6FD}_{0z}^{-1/6}$
when
![]() $B_{0y}\approx B_{0z}$
and
$B_{0y}\approx B_{0z}$
and
![]() $S/\unicode[STIX]{x1D6FA}=3/2$
(see (A 2)). In this fastest-growing mode, the relative amplitudes of the various components are
$S/\unicode[STIX]{x1D6FA}=3/2$
(see (A 2)). In this fastest-growing mode, the relative amplitudes of the various components are
![]() $\unicode[STIX]{x1D6FD}_{0}^{-2/3}\unicode[STIX]{x1D6FF}B_{x}/B_{0}\sim \unicode[STIX]{x1D6FD}_{0}^{-1/3}\unicode[STIX]{x1D6FF}B_{y}/B_{0}\sim \unicode[STIX]{x1D6FD}_{0}^{-5/6}\unicode[STIX]{x1D6FF}u_{x}/v_{A}\sim \unicode[STIX]{x1D6FD}_{0}^{-5/6}\unicode[STIX]{x1D6FF}u_{y}/v_{A}\sim \unicode[STIX]{x1D6FF}p_{\bot ,\Vert }/p_{0}$
(unlike the standard MRI, where
$\unicode[STIX]{x1D6FD}_{0}^{-2/3}\unicode[STIX]{x1D6FF}B_{x}/B_{0}\sim \unicode[STIX]{x1D6FD}_{0}^{-1/3}\unicode[STIX]{x1D6FF}B_{y}/B_{0}\sim \unicode[STIX]{x1D6FD}_{0}^{-5/6}\unicode[STIX]{x1D6FF}u_{x}/v_{A}\sim \unicode[STIX]{x1D6FD}_{0}^{-5/6}\unicode[STIX]{x1D6FF}u_{y}/v_{A}\sim \unicode[STIX]{x1D6FF}p_{\bot ,\Vert }/p_{0}$
(unlike the standard MRI, where
![]() $\unicode[STIX]{x1D6FF}B_{x}/B_{0}\sim \unicode[STIX]{x1D6FF}B_{y}/B_{0}\sim \unicode[STIX]{x1D6FF}u_{x}/v_{A}\sim \unicode[STIX]{x1D6FF}u_{y}/v_{A}$
). While we shall use these scalings below in our discussion of the nonlinear behaviour of MRI modes, we caution that they only apply at rather high
$\unicode[STIX]{x1D6FF}B_{x}/B_{0}\sim \unicode[STIX]{x1D6FF}B_{y}/B_{0}\sim \unicode[STIX]{x1D6FF}u_{x}/v_{A}\sim \unicode[STIX]{x1D6FF}u_{y}/v_{A}$
). While we shall use these scalings below in our discussion of the nonlinear behaviour of MRI modes, we caution that they only apply at rather high
![]() $\unicode[STIX]{x1D6FD}_{0}$
, a problem that is exacerbated if
$\unicode[STIX]{x1D6FD}_{0}$
, a problem that is exacerbated if
![]() $B_{0y}/B_{0z}\neq 1$
. At more moderate
$B_{0y}/B_{0z}\neq 1$
. At more moderate
![]() $\unicode[STIX]{x1D6FD}_{0}$
, as feasible for simulations,
$\unicode[STIX]{x1D6FD}_{0}$
, as feasible for simulations,
![]() $k_{\text{max}}$
tends towards its value for the standard MRI,
$k_{\text{max}}$
tends towards its value for the standard MRI,
![]() $k_{\text{max}}v_{Az}/\unicode[STIX]{x1D6FA}\approx 1$
(see figure 7). It is also worth noting that the dispersion relation,
$k_{\text{max}}v_{Az}/\unicode[STIX]{x1D6FA}\approx 1$
(see figure 7). It is also worth noting that the dispersion relation,
![]() $\unicode[STIX]{x1D6FE}(k)$
, varies only slowly around
$\unicode[STIX]{x1D6FE}(k)$
, varies only slowly around
![]() $k=k_{\text{max}}$
(see e.g. dotted curve in figure 1). This implies that, if starting from random initial conditions, a long time would be required before the fastest-growing mode dominates, suggesting that when nonlinear effects become important there will likely still be several modes of similar amplitudes. With these caveats duly noted, in our discussion of nonlinear effects below (§ 3.3), we will consider only the fastest-growing KMRI mode (i.e. set
$k=k_{\text{max}}$
(see e.g. dotted curve in figure 1). This implies that, if starting from random initial conditions, a long time would be required before the fastest-growing mode dominates, suggesting that when nonlinear effects become important there will likely still be several modes of similar amplitudes. With these caveats duly noted, in our discussion of nonlinear effects below (§ 3.3), we will consider only the fastest-growing KMRI mode (i.e. set
![]() $k=k_{\text{max}}$
) and use the above scalings, rather than keep
$k=k_{\text{max}}$
) and use the above scalings, rather than keep
![]() $k$
arbitrary.
$k$
arbitrary.
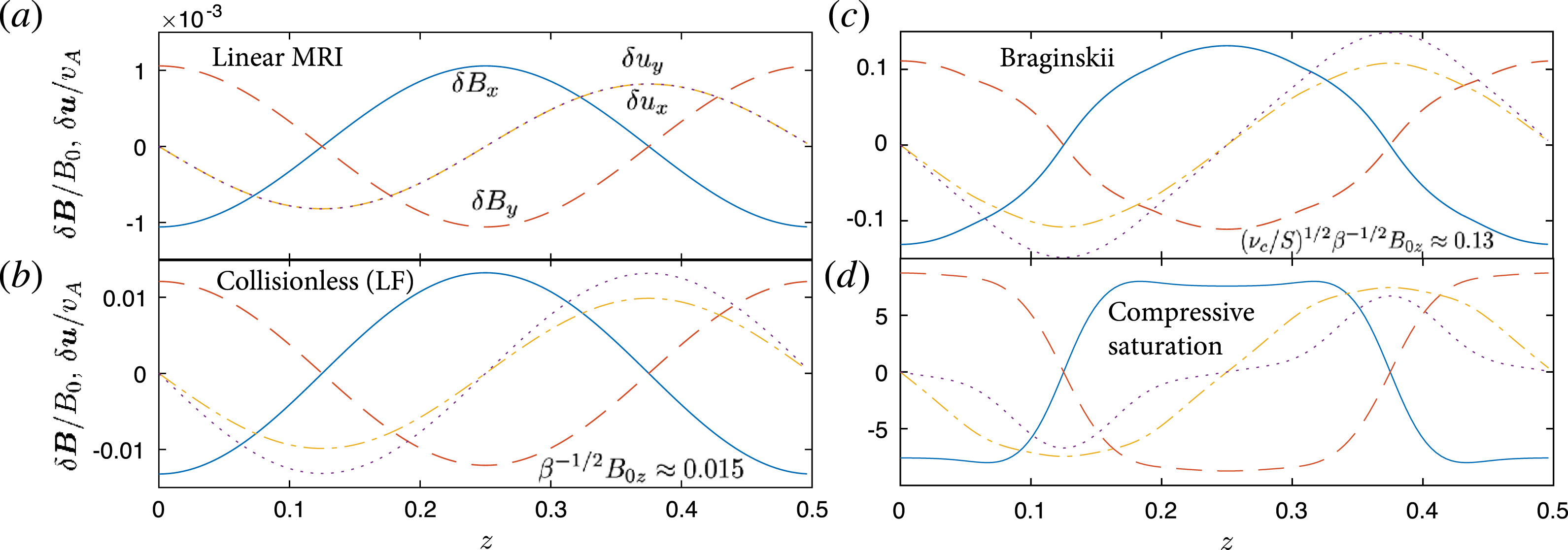
Figure 2. The structure of a kinetic MRI mode evolving in a vertical background field
![]() $B_{0z}$
in various regimes, as computed from the 1-D LF model (with
$B_{0z}$
in various regimes, as computed from the 1-D LF model (with
![]() $\unicode[STIX]{x1D708}_{c}\neq 0$
in panel c). We take
$\unicode[STIX]{x1D708}_{c}\neq 0$
in panel c). We take
![]() $\unicode[STIX]{x1D6FD}_{0}=337$
in a domain with
$\unicode[STIX]{x1D6FD}_{0}=337$
in a domain with
![]() $\unicode[STIX]{x1D6FA}L_{z}/c_{s}=1$
, such that the peak of the MRI dispersion relation (i.e. the maximum
$\unicode[STIX]{x1D6FA}L_{z}/c_{s}=1$
, such that the peak of the MRI dispersion relation (i.e. the maximum
![]() $\unicode[STIX]{x1D6FE}$
) is at
$\unicode[STIX]{x1D6FE}$
) is at
![]() $k=2\times 2\unicode[STIX]{x03C0}/L_{z}$
(each panel shows only half of a scale height). Each plot illustrates
$k=2\times 2\unicode[STIX]{x03C0}/L_{z}$
(each panel shows only half of a scale height). Each plot illustrates
![]() $\unicode[STIX]{x1D6FF}B_{x}$
(blue solid line),
$\unicode[STIX]{x1D6FF}B_{x}$
(blue solid line),
![]() $\unicode[STIX]{x1D6FF}B_{y}$
(red dashed line),
$\unicode[STIX]{x1D6FF}B_{y}$
(red dashed line),
![]() $\unicode[STIX]{x1D6FF}u_{x}$
(yellow dot-dashed line) and
$\unicode[STIX]{x1D6FF}u_{x}$
(yellow dot-dashed line) and
![]() $\unicode[STIX]{x1D6FF}u_{y}$
(purple dotted line). The various panels show: (a) the linear KMRI mode (this is the initial conditions for each simulation), which is identical in structure to an MHD MRI mode at these parameters; (b) the collisionless MRI mode when
$\unicode[STIX]{x1D6FF}u_{y}$
(purple dotted line). The various panels show: (a) the linear KMRI mode (this is the initial conditions for each simulation), which is identical in structure to an MHD MRI mode at these parameters; (b) the collisionless MRI mode when
![]() $\unicode[STIX]{x0394}p$
reaches the mirror limit (
$\unicode[STIX]{x0394}p$
reaches the mirror limit (
![]() $\unicode[STIX]{x1D6FF}B\sim \unicode[STIX]{x1D6FD}^{-1/2}B_{0z}\approx 0.015$
), which remains very nearly sinusoidal because the heat fluxes make
$\unicode[STIX]{x1D6FF}B\sim \unicode[STIX]{x1D6FD}^{-1/2}B_{0z}\approx 0.015$
), which remains very nearly sinusoidal because the heat fluxes make
![]() $\unicode[STIX]{x0394}p$
spatially uniform; (c) a mode in the high-collisionality Braginskii regime (with
$\unicode[STIX]{x0394}p$
spatially uniform; (c) a mode in the high-collisionality Braginskii regime (with
![]() $\unicode[STIX]{x1D708}_{c}/S=\unicode[STIX]{x1D6FD}_{0}^{3/4}$
) when
$\unicode[STIX]{x1D708}_{c}/S=\unicode[STIX]{x1D6FD}_{0}^{3/4}$
) when
![]() $\unicode[STIX]{x0394}p$
reaches the mirror limit (at
$\unicode[STIX]{x0394}p$
reaches the mirror limit (at
![]() $\unicode[STIX]{x1D6FF}B\sim (\unicode[STIX]{x1D708}_{c}/S)^{1/2}\unicode[STIX]{x1D6FD}^{-1/2}B_{0z}\approx 0.13$
), which is non-sinusoidal because of the
$\unicode[STIX]{x1D6FF}B\sim (\unicode[STIX]{x1D708}_{c}/S)^{1/2}\unicode[STIX]{x1D6FD}^{-1/2}B_{0z}\approx 0.13$
), which is non-sinusoidal because of the
![]() $O(1)$
spatial variation in
$O(1)$
spatial variation in
![]() $\unicode[STIX]{x0394}p$
; (d) the MRI mode at very large amplitudes, when compressibility becomes important. The structure of this final compressible stage of evolution is the same across all models, including standard (collisional) MHD.
$\unicode[STIX]{x0394}p$
; (d) the MRI mode at very large amplitudes, when compressibility becomes important. The structure of this final compressible stage of evolution is the same across all models, including standard (collisional) MHD.
3.2 Nonlinear KMRI: vertical magnetic field
In this section, we consider the nonlinear evolution of the MRI in a vertical background field. In this case the linear dispersion relation is identical to that obtained in ideal MHD. However, we shall show that the modes are (modestly) nonlinearly modified by the pressure anisotropy at low amplitudes
![]() $\unicode[STIX]{x1D6FF}B\sim \unicode[STIX]{x1D6FD}^{-1/2}B_{0}$
. To do so, we first describe the evolution of a truly collisionless mode using the LF closure with
$\unicode[STIX]{x1D6FF}B\sim \unicode[STIX]{x1D6FD}^{-1/2}B_{0}$
. To do so, we first describe the evolution of a truly collisionless mode using the LF closure with
![]() $\unicode[STIX]{x1D708}_{c}=0$
(§ 3.2.1), and then examine the weakly collisional Braginskii case in § 3.2.2.
$\unicode[STIX]{x1D708}_{c}=0$
(§ 3.2.1), and then examine the weakly collisional Braginskii case in § 3.2.2.
3.2.1 Collisionless (LF) regime
A maximally unstable MRI mode satisfies
The mirror threshold is reached at
![]() $\unicode[STIX]{x1D6E5}=1/\unicode[STIX]{x1D6FD}$
, when
$\unicode[STIX]{x1D6E5}=1/\unicode[STIX]{x1D6FD}$
, when
![]() $\unicode[STIX]{x1D6FF}B/B_{0z}\sim \unicode[STIX]{x1D6FD}_{0}^{-1/2}$
. As discussed in § 3.1, a positive pressure anisotropy modifies the MRI mode by effectively increasing the magnetic tension, and the mode will be stabilized if
$\unicode[STIX]{x1D6FF}B/B_{0z}\sim \unicode[STIX]{x1D6FD}_{0}^{-1/2}$
. As discussed in § 3.1, a positive pressure anisotropy modifies the MRI mode by effectively increasing the magnetic tension, and the mode will be stabilized if
![]() $kv_{A}\sqrt{1+\unicode[STIX]{x0394}(t)\unicode[STIX]{x1D6FD}_{0}/2}\geqslant \sqrt{2S\unicode[STIX]{x1D6FA}}$
. Fortunately, for a mode near the peak growth rate,
$kv_{A}\sqrt{1+\unicode[STIX]{x0394}(t)\unicode[STIX]{x1D6FD}_{0}/2}\geqslant \sqrt{2S\unicode[STIX]{x1D6FA}}$
. Fortunately, for a mode near the peak growth rate,
![]() $kv_{A}=\sqrt{S(\unicode[STIX]{x1D6FA}-S/4)}$
, this stabilization does not occur, because the fast-growing mirror fluctuations limit
$kv_{A}=\sqrt{S(\unicode[STIX]{x1D6FA}-S/4)}$
, this stabilization does not occur, because the fast-growing mirror fluctuations limit
![]() $\sqrt{1+\unicode[STIX]{x0394}(t)\unicode[STIX]{x1D6FD}_{0}/2}$
to values at or below
$\sqrt{1+\unicode[STIX]{x0394}(t)\unicode[STIX]{x1D6FD}_{0}/2}$
to values at or below
![]() $\sqrt{3/2}$
. As shown in figure 2(b), this pressure anisotropy causes a rather minor modification to the shape of the MRI mode because
$\sqrt{3/2}$
. As shown in figure 2(b), this pressure anisotropy causes a rather minor modification to the shape of the MRI mode because
![]() $\unicode[STIX]{x0394}p$
is almost spatially constant, decreasing
$\unicode[STIX]{x0394}p$
is almost spatially constant, decreasing
![]() $u_{x}$
and
$u_{x}$
and
![]() $B_{y}$
relative to
$B_{y}$
relative to
![]() $u_{y}$
and
$u_{y}$
and
![]() $B_{x}$
in the same way as for an MHD MRI mode that is not at the fastest-growing wavelength.Footnote
6
$B_{x}$
in the same way as for an MHD MRI mode that is not at the fastest-growing wavelength.Footnote
6
As the mode continues to evolve to larger amplitudes
![]() $\unicode[STIX]{x1D6FF}B/B_{0z}\gtrsim \unicode[STIX]{x1D6FD}_{0}^{-1/2}$
, the pressure anisotropy remains limited by mirror fluctuations. Leaving aside, for the moment, questions related to how the mode disrupts and becomes turbulent, there are two other amplitudes of interest: (i) when the mode amplitude surpasses the background field at
$\unicode[STIX]{x1D6FF}B/B_{0z}\gtrsim \unicode[STIX]{x1D6FD}_{0}^{-1/2}$
, the pressure anisotropy remains limited by mirror fluctuations. Leaving aside, for the moment, questions related to how the mode disrupts and becomes turbulent, there are two other amplitudes of interest: (i) when the mode amplitude surpasses the background field at
![]() $\unicode[STIX]{x1D6FF}B/B_{0z}\sim 1$
, and (ii) when compressibility becomes important at
$\unicode[STIX]{x1D6FF}B/B_{0z}\sim 1$
, and (ii) when compressibility becomes important at
![]() $\unicode[STIX]{x1D6FF}B/B_{0z}\sim \unicode[STIX]{x1D6FD}_{0}^{1/2}$
(
$\unicode[STIX]{x1D6FF}B/B_{0z}\sim \unicode[STIX]{x1D6FD}_{0}^{1/2}$
(
![]() $\unicode[STIX]{x1D6FF}u\sim c_{s}$
). Interestingly, if the pressure anisotropy is efficiently limited by mirror fluctuations,
$\unicode[STIX]{x1D6FF}u\sim c_{s}$
). Interestingly, if the pressure anisotropy is efficiently limited by mirror fluctuations,
![]() $\unicode[STIX]{x0394}p=B^{2}/8\unicode[STIX]{x03C0}$
, then the pressure anisotropy nonlinearity has little effect:
$\unicode[STIX]{x0394}p=B^{2}/8\unicode[STIX]{x03C0}$
, then the pressure anisotropy nonlinearity has little effect:
since
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FF}\boldsymbol{B}\approx 0$
for an MRI channel mode (Goodman & Xu Reference Goodman and Xu1994). Thus, once
$\unicode[STIX]{x1D6FF}\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FF}\boldsymbol{B}\approx 0$
for an MRI channel mode (Goodman & Xu Reference Goodman and Xu1994). Thus, once
![]() $\unicode[STIX]{x1D6FF}B_{x}\sim \unicode[STIX]{x1D6FF}B_{y}\gtrsim B_{0}$
, the effect of the pressure-anisotropy nonlinearity on the mode remains identical to when
$\unicode[STIX]{x1D6FF}B_{x}\sim \unicode[STIX]{x1D6FF}B_{y}\gtrsim B_{0}$
, the effect of the pressure-anisotropy nonlinearity on the mode remains identical to when
![]() $\unicode[STIX]{x1D6FF}B_{x}\sim \unicode[STIX]{x1D6FF}B_{y}\lesssim B_{0}$
, even though the pressure anisotropy has a large (
$\unicode[STIX]{x1D6FF}B_{x}\sim \unicode[STIX]{x1D6FF}B_{y}\lesssim B_{0}$
, even though the pressure anisotropy has a large (
![]() $\unicode[STIX]{x0394}p\sim \unicode[STIX]{x1D6FF}B^{2}$
) variation in space (i.e. the change is simply a modified magnetic tension, as shown in figure 2
b). In other words, because
$\unicode[STIX]{x0394}p\sim \unicode[STIX]{x1D6FF}B^{2}$
) variation in space (i.e. the change is simply a modified magnetic tension, as shown in figure 2
b). In other words, because
![]() $\unicode[STIX]{x0394}p\propto B^{2}$
, there is no significant change to the mode as the mode amplitude surpasses the background field strength.
$\unicode[STIX]{x0394}p\propto B^{2}$
, there is no significant change to the mode as the mode amplitude surpasses the background field strength.
The final phase of evolution, once
![]() $\unicode[STIX]{x1D6FF}B\sim \unicode[STIX]{x1D6FD}^{1/2}B_{0}$
(i.e.
$\unicode[STIX]{x1D6FF}B\sim \unicode[STIX]{x1D6FD}^{1/2}B_{0}$
(i.e.
![]() $\unicode[STIX]{x1D6FF}u\sim c_{s}$
), is then very similar to standard MHD, and the mode develops a rather distinctive shape, which we illustrate in figure 2(d). Because the nonlinearity is dominated at this point in the evolution by inhomogeneities in the density, this mode shape appears generically in all of the models studied here (including compressible MHD) across a wide range of parameters (cf. Latter et al.
Reference Latter, Lesaffre and Balbus2009).
$\unicode[STIX]{x1D6FF}u\sim c_{s}$
), is then very similar to standard MHD, and the mode develops a rather distinctive shape, which we illustrate in figure 2(d). Because the nonlinearity is dominated at this point in the evolution by inhomogeneities in the density, this mode shape appears generically in all of the models studied here (including compressible MHD) across a wide range of parameters (cf. Latter et al.
Reference Latter, Lesaffre and Balbus2009).
3.2.2 Weakly collisional (Braginskii) regime
In the Braginskii regime, which is valid for
![]() $\overline{\unicode[STIX]{x1D708}}_{c}\equiv \unicode[STIX]{x1D708}_{c}/S\sim \unicode[STIX]{x1D708}_{c}/\unicode[STIX]{x1D6FE}\gg 1$
and is relevant (i.e. represents a potentially significant correction to standard MHD) when
$\overline{\unicode[STIX]{x1D708}}_{c}\equiv \unicode[STIX]{x1D708}_{c}/S\sim \unicode[STIX]{x1D708}_{c}/\unicode[STIX]{x1D6FE}\gg 1$
and is relevant (i.e. represents a potentially significant correction to standard MHD) when
![]() $\overline{\unicode[STIX]{x1D708}}_{c}\ll \unicode[STIX]{x1D6FD}_{0}$
, there are two subregimes. In the moderate-collisionality regime,
$\overline{\unicode[STIX]{x1D708}}_{c}\ll \unicode[STIX]{x1D6FD}_{0}$
, there are two subregimes. In the moderate-collisionality regime,
![]() $\overline{\unicode[STIX]{x1D708}}_{c}\ll \unicode[STIX]{x1D6FD}_{0}^{1/2}$
, the heat fluxes play a very significant role and smooth the pressure anisotropy spatially, as occurs in the collisionless case described in § 3.2.1. In the high-collisionality regime,
$\overline{\unicode[STIX]{x1D708}}_{c}\ll \unicode[STIX]{x1D6FD}_{0}^{1/2}$
, the heat fluxes play a very significant role and smooth the pressure anisotropy spatially, as occurs in the collisionless case described in § 3.2.1. In the high-collisionality regime,
![]() $\overline{\unicode[STIX]{x1D708}}_{c}\gg \unicode[STIX]{x1D6FD}_{0}^{1/2}$
, the heat fluxes are sub-dominant and do not play a significant dynamical role, leading to
$\overline{\unicode[STIX]{x1D708}}_{c}\gg \unicode[STIX]{x1D6FD}_{0}^{1/2}$
, the heat fluxes are sub-dominant and do not play a significant dynamical role, leading to
![]() $\unicode[STIX]{x0394}p$
profiles that vary significantly in space. For more information, see § B.4 and appendix B of Squire et al. (Reference Squire, Schekochihin and Quataert2017).
$\unicode[STIX]{x0394}p$
profiles that vary significantly in space. For more information, see § B.4 and appendix B of Squire et al. (Reference Squire, Schekochihin and Quataert2017).
In the moderate-collisionality regime, up to
![]() $\overline{\unicode[STIX]{x1D708}}_{c}\lesssim \unicode[STIX]{x1D6FD}_{0}^{1/2}$
, the behaviour of the mode at amplitudes
$\overline{\unicode[STIX]{x1D708}}_{c}\lesssim \unicode[STIX]{x1D6FD}_{0}^{1/2}$
, the behaviour of the mode at amplitudes
![]() $\unicode[STIX]{x1D6FF}B\lesssim (\unicode[STIX]{x1D6FD}_{0}/\overline{\unicode[STIX]{x1D708}}_{c})^{1/2}B_{0}$
(see below) is effectively identical to the collisionless regime discussed in § 3.2.1. In particular, the pressure anisotropy that develops from the growing mode with
$\unicode[STIX]{x1D6FF}B\lesssim (\unicode[STIX]{x1D6FD}_{0}/\overline{\unicode[STIX]{x1D708}}_{c})^{1/2}B_{0}$
(see below) is effectively identical to the collisionless regime discussed in § 3.2.1. In particular, the pressure anisotropy that develops from the growing mode with
![]() $\unicode[STIX]{x1D6FF}B\ll B_{0}$
is
$\unicode[STIX]{x1D6FF}B\ll B_{0}$
is
because the heat fluxes are smoothing
![]() $\unicode[STIX]{x0394}p$
faster than it is being created (by some factor between
$\unicode[STIX]{x0394}p$
faster than it is being created (by some factor between
![]() $\unicode[STIX]{x1D6FD}_{0}^{1/2}$
and
$\unicode[STIX]{x1D6FD}_{0}^{1/2}$
and
![]() $1$
, depending on
$1$
, depending on
![]() $\overline{\unicode[STIX]{x1D708}}_{c}\,\unicode[STIX]{x1D6FD}_{0}^{-1/2}$
; see Squire et al.
Reference Squire, Schekochihin and Quataert2017). Thus, by the time that
$\overline{\unicode[STIX]{x1D708}}_{c}\,\unicode[STIX]{x1D6FD}_{0}^{-1/2}$
; see Squire et al.
Reference Squire, Schekochihin and Quataert2017). Thus, by the time that
![]() $\unicode[STIX]{x0394}p$
reaches the mirror limit (i.e. when
$\unicode[STIX]{x0394}p$
reaches the mirror limit (i.e. when
![]() $\unicode[STIX]{x1D6FF}B\sim (\overline{\unicode[STIX]{x1D708}}_{c}/\unicode[STIX]{x1D6FD}_{0})^{1/2}B_{0}$
), it is nearly smooth in space, implying that the same conclusions reached in the collisionless limit also apply here. The same is then true as the mode continues growing to
$\unicode[STIX]{x1D6FF}B\sim (\overline{\unicode[STIX]{x1D708}}_{c}/\unicode[STIX]{x1D6FD}_{0})^{1/2}B_{0}$
), it is nearly smooth in space, implying that the same conclusions reached in the collisionless limit also apply here. The same is then true as the mode continues growing to
![]() $\unicode[STIX]{x1D6FF}B\gtrsim B_{0}$
(but
$\unicode[STIX]{x1D6FF}B\gtrsim B_{0}$
(but
![]() $\unicode[STIX]{x1D6FF}B\lesssim (\unicode[STIX]{x1D6FD}_{0}/\overline{\unicode[STIX]{x1D708}}_{c})^{1/2}B_{0}$
); it forces
$\unicode[STIX]{x1D6FF}B\lesssim (\unicode[STIX]{x1D6FD}_{0}/\overline{\unicode[STIX]{x1D708}}_{c})^{1/2}B_{0}$
); it forces
![]() $\unicode[STIX]{x0394}p$
to the mirror limit everywhere in space, implying the mode is not strongly affected by the pressure-anisotropy nonlinearity (see (3.3)).
$\unicode[STIX]{x0394}p$
to the mirror limit everywhere in space, implying the mode is not strongly affected by the pressure-anisotropy nonlinearity (see (3.3)).
In the high-collisionality regime,
![]() $\overline{\unicode[STIX]{x1D708}}_{c}\gg \unicode[STIX]{x1D6FD}_{0}^{1/2}$
, the heat fluxes do not significantly smooth spatial variation in
$\overline{\unicode[STIX]{x1D708}}_{c}\gg \unicode[STIX]{x1D6FD}_{0}^{1/2}$
, the heat fluxes do not significantly smooth spatial variation in
![]() $\unicode[STIX]{x0394}p$
and we must modify various aspects of the conclusions from the previous section. The pressure anisotropy that develops from the growing mode (for
$\unicode[STIX]{x0394}p$
and we must modify various aspects of the conclusions from the previous section. The pressure anisotropy that develops from the growing mode (for
![]() $\unicode[STIX]{x1D6FF}B\ll B_{0}$
) is now spatially inhomogeneous:
$\unicode[STIX]{x1D6FF}B\ll B_{0}$
) is now spatially inhomogeneous:
This implies that, as the pressure anisotropy first reaches the mirror limit in some regions of space (near the antinodes of the mode, where
![]() $\text{d}_{t}\text{ln}~B$
is largest), it also changes the shape of the mode, viz., it couples different Fourier components of
$\text{d}_{t}\text{ln}~B$
is largest), it also changes the shape of the mode, viz., it couples different Fourier components of
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{B}$
and
$\unicode[STIX]{x1D6FF}\boldsymbol{B}$
and
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{u}$
. This causes minor modifications to the shape of the mode, which are shown in figure 2(c) for
$\unicode[STIX]{x1D6FF}\boldsymbol{u}$
. This causes minor modifications to the shape of the mode, which are shown in figure 2(c) for
![]() $\overline{\unicode[STIX]{x1D708}}_{c}=\unicode[STIX]{x1D6FD}_{0}^{3/4}$
(i.e. in the middle of the high-collisionality regime; the shape changes at other
$\overline{\unicode[STIX]{x1D708}}_{c}=\unicode[STIX]{x1D6FD}_{0}^{3/4}$
(i.e. in the middle of the high-collisionality regime; the shape changes at other
![]() $\overline{\unicode[STIX]{x1D708}}_{c}$
and
$\overline{\unicode[STIX]{x1D708}}_{c}$
and
![]() $\unicode[STIX]{x1D6FD}_{0}$
are generally similar to this). As the mode grows further,
$\unicode[STIX]{x1D6FD}_{0}$
are generally similar to this). As the mode grows further,
![]() $\unicode[STIX]{x0394}p$
becomes limited by the mirror instability (
$\unicode[STIX]{x0394}p$
becomes limited by the mirror instability (
![]() $\unicode[STIX]{x0394}p\propto B_{0}^{2}+\unicode[STIX]{x1D6FF}B^{2}$
) across a larger region of space, implying (by the arguments above) that the mode regains its sinusoidal shape (albeit briefly, see next paragraph).
$\unicode[STIX]{x0394}p\propto B_{0}^{2}+\unicode[STIX]{x1D6FF}B^{2}$
) across a larger region of space, implying (by the arguments above) that the mode regains its sinusoidal shape (albeit briefly, see next paragraph).
There is one final effect, not included in the collisionless discussion, which occurs in both the moderate-collisionality and high-collisionality Braginskii regimes at large mode amplitudes,
![]() $\unicode[STIX]{x1D6FF}B\gtrsim (\unicode[STIX]{x1D6FD}_{0}/\overline{\unicode[STIX]{x1D708}}_{c})^{1/2}B_{0}$
. The difference compared to the collisionless case arises because, in the Braginskii regime,
$\unicode[STIX]{x1D6FF}B\gtrsim (\unicode[STIX]{x1D6FD}_{0}/\overline{\unicode[STIX]{x1D708}}_{c})^{1/2}B_{0}$
. The difference compared to the collisionless case arises because, in the Braginskii regime,
![]() $\unicode[STIX]{x0394}p$
is proportional to the current value of
$\unicode[STIX]{x0394}p$
is proportional to the current value of
![]() $\hat{\boldsymbol{b}}\hat{\boldsymbol{b}}\,\boldsymbol{ : }\,\unicode[STIX]{x1D735}\boldsymbol{u}$
rather than to its time history. Once
$\hat{\boldsymbol{b}}\hat{\boldsymbol{b}}\,\boldsymbol{ : }\,\unicode[STIX]{x1D735}\boldsymbol{u}$
rather than to its time history. Once
![]() $\unicode[STIX]{x1D6FF}B\gtrsim B_{0}$
, this value
$\unicode[STIX]{x1D6FF}B\gtrsim B_{0}$
, this value
![]() $\hat{\boldsymbol{b}}\hat{\boldsymbol{b}}\,\boldsymbol{ : }\,\unicode[STIX]{x1D735}\boldsymbol{u}\approx -S\unicode[STIX]{x1D6FF}B_{x}\unicode[STIX]{x1D6FF}B_{y}/\unicode[STIX]{x1D6FF}B^{2}$
becomes constant in time, despite the fact that
$\hat{\boldsymbol{b}}\hat{\boldsymbol{b}}\,\boldsymbol{ : }\,\unicode[STIX]{x1D735}\boldsymbol{u}\approx -S\unicode[STIX]{x1D6FF}B_{x}\unicode[STIX]{x1D6FF}B_{y}/\unicode[STIX]{x1D6FF}B^{2}$
becomes constant in time, despite the fact that
![]() $B^{2}\approx \unicode[STIX]{x1D6FF}B^{2}$
is growing. Thus,
$B^{2}\approx \unicode[STIX]{x1D6FF}B^{2}$
is growing. Thus,
![]() $\unicode[STIX]{x0394}p$
moves back below the mirror limit when
$\unicode[STIX]{x0394}p$
moves back below the mirror limit when
![]() $\unicode[STIX]{x1D6FF}B^{2}\gtrsim p_{0}/\overline{\unicode[STIX]{x1D708}}_{c}$
, viz., when
$\unicode[STIX]{x1D6FF}B^{2}\gtrsim p_{0}/\overline{\unicode[STIX]{x1D708}}_{c}$
, viz., when
![]() $\unicode[STIX]{x1D6FF}B\gtrsim (\unicode[STIX]{x1D6FD}_{0}/\overline{\unicode[STIX]{x1D708}}_{c})^{1/2}B_{0}$
. This occurs before compressibility affects the mode (at
$\unicode[STIX]{x1D6FF}B\gtrsim (\unicode[STIX]{x1D6FD}_{0}/\overline{\unicode[STIX]{x1D708}}_{c})^{1/2}B_{0}$
. This occurs before compressibility affects the mode (at
![]() $\unicode[STIX]{x1D6FF}B\sim \unicode[STIX]{x1D6FD}_{0}^{1/2}B_{0}$
), and causes the pressure anisotropy to vary in space, which in turn modifies the shape of the mode. These modifications are very minor, even at very high
$\unicode[STIX]{x1D6FF}B\sim \unicode[STIX]{x1D6FD}_{0}^{1/2}B_{0}$
), and causes the pressure anisotropy to vary in space, which in turn modifies the shape of the mode. These modifications are very minor, even at very high
![]() $\unicode[STIX]{x1D6FD}_{0}\sim 10^{5}$
and high
$\unicode[STIX]{x1D6FD}_{0}\sim 10^{5}$
and high
![]() $\overline{\unicode[STIX]{x1D708}}_{c}$
(not shown), and so it seems unlikely that they should modify mode saturation in three dimensions in any significant way. As the amplitude approaches
$\overline{\unicode[STIX]{x1D708}}_{c}$
(not shown), and so it seems unlikely that they should modify mode saturation in three dimensions in any significant way. As the amplitude approaches
![]() $\unicode[STIX]{x1D6FF}B\sim \unicode[STIX]{x1D6FD}_{0}^{1/2}B_{0}$
, the mode is affected by compressibility in exactly the same way as is the collisionless (or MHD) MRI (see figure 2
d).
$\unicode[STIX]{x1D6FF}B\sim \unicode[STIX]{x1D6FD}_{0}^{1/2}B_{0}$
, the mode is affected by compressibility in exactly the same way as is the collisionless (or MHD) MRI (see figure 2
d).

Figure 3. (a) Energy evolution of each component of the growing KMRI mode in a mixed-azimuthal–vertical field with
![]() $B_{0y}=B_{0z}$
, at
$B_{0y}=B_{0z}$
, at
![]() $\unicode[STIX]{x1D6FD}_{0}=5000$
(
$\unicode[STIX]{x1D6FD}_{0}=5000$
(
![]() $\unicode[STIX]{x1D6FD}_{0z}=10\,000$
) in a domain such that
$\unicode[STIX]{x1D6FD}_{0z}=10\,000$
) in a domain such that
![]() $\unicode[STIX]{x1D6FA}L_{z}/c_{s}=1$
. We show
$\unicode[STIX]{x1D6FA}L_{z}/c_{s}=1$
. We show
![]() $\unicode[STIX]{x1D6FF}B_{x}$
(solid purple line;
$\unicode[STIX]{x1D6FF}B_{x}$
(solid purple line;
![]() $E_{\text{MRI}}=\int \text{d}z\,\unicode[STIX]{x1D6FF}B_{x}^{2}/8\unicode[STIX]{x03C0}$
),
$E_{\text{MRI}}=\int \text{d}z\,\unicode[STIX]{x1D6FF}B_{x}^{2}/8\unicode[STIX]{x03C0}$
),
![]() $\unicode[STIX]{x1D6FF}B_{y}$
(solid green line;
$\unicode[STIX]{x1D6FF}B_{y}$
(solid green line;
![]() $E_{\text{MRI}}=\int \text{d}z\,\unicode[STIX]{x1D6FF}B_{y}^{2}/8\unicode[STIX]{x03C0}$
),
$E_{\text{MRI}}=\int \text{d}z\,\unicode[STIX]{x1D6FF}B_{y}^{2}/8\unicode[STIX]{x03C0}$
),
![]() $\unicode[STIX]{x1D6FF}u_{x}$
(dashed blue line;
$\unicode[STIX]{x1D6FF}u_{x}$
(dashed blue line;
![]() $E_{\text{MRI}}=\int \text{d}z\,\unicode[STIX]{x1D70C}\unicode[STIX]{x1D6FF}u_{x}^{2}/2$
), and
$E_{\text{MRI}}=\int \text{d}z\,\unicode[STIX]{x1D70C}\unicode[STIX]{x1D6FF}u_{x}^{2}/2$
), and
![]() $\unicode[STIX]{x1D6FF}u_{y}$
(dashed red line;
$\unicode[STIX]{x1D6FF}u_{y}$
(dashed red line;
![]() $E_{\text{MRI}}=\int \text{d}z\,\unicode[STIX]{x1D70C}\unicode[STIX]{x1D6FF}u_{y}^{2}/2$
). The calculation, which uses the 1-D LF model (2.1)–(2.7) with
$E_{\text{MRI}}=\int \text{d}z\,\unicode[STIX]{x1D70C}\unicode[STIX]{x1D6FF}u_{y}^{2}/2$
). The calculation, which uses the 1-D LF model (2.1)–(2.7) with
![]() $\unicode[STIX]{x1D708}_{c}=0$
, is initialized with random Fourier amplitudes, scaled by
$\unicode[STIX]{x1D708}_{c}=0$
, is initialized with random Fourier amplitudes, scaled by
![]() $k^{-2}$
(initial phase of evolution not shown for clarity). For comparison, we also show the thermal energy (yellow dot-dashed line) and the energy of the background magnetic field (grey dot-dashed line). Following the linear phase with large growth rate (Region 1), the linearly perturbed pressure anisotropy reaches the mirror and firehose limits when
$k^{-2}$
(initial phase of evolution not shown for clarity). For comparison, we also show the thermal energy (yellow dot-dashed line) and the energy of the background magnetic field (grey dot-dashed line). Following the linear phase with large growth rate (Region 1), the linearly perturbed pressure anisotropy reaches the mirror and firehose limits when
![]() $\unicode[STIX]{x1D6FF}B_{y}\sim \unicode[STIX]{x1D6FD}_{0}^{-2/3}B_{0y}$
,
$\unicode[STIX]{x1D6FF}B_{y}\sim \unicode[STIX]{x1D6FD}_{0}^{-2/3}B_{0y}$
,
![]() $\unicode[STIX]{x1D6FF}B_{x}\sim \unicode[STIX]{x1D6FD}_{0}^{-1/3}B_{0y}$
. There follows a transition phase (Region 2) in which the perturbed pressure anisotropy can no longer contribute to the instability and the mode moves to the much shorter wavelengths characteristic of the standard MRI. Then, once
$\unicode[STIX]{x1D6FF}B_{x}\sim \unicode[STIX]{x1D6FD}_{0}^{-1/3}B_{0y}$
. There follows a transition phase (Region 2) in which the perturbed pressure anisotropy can no longer contribute to the instability and the mode moves to the much shorter wavelengths characteristic of the standard MRI. Then, once
![]() $\unicode[STIX]{x1D6FF}B_{y}>B_{0y}$
, the mode grows similarly to the vertical-field KMRI (Region 3) with
$\unicode[STIX]{x1D6FF}B_{y}>B_{0y}$
, the mode grows similarly to the vertical-field KMRI (Region 3) with
![]() $\unicode[STIX]{x1D6E5}$
at the mirror limit, until finally it is affected by compressibility in the same way as illustrated in figure 2(d) (Region 4). (b) Spatial structure of the azimuthal-field KMRI mode at a variety of times corresponding to ‘
$\unicode[STIX]{x1D6E5}$
at the mirror limit, until finally it is affected by compressibility in the same way as illustrated in figure 2(d) (Region 4). (b) Spatial structure of the azimuthal-field KMRI mode at a variety of times corresponding to ‘
![]() $\times$
’ markers in panel (a), which are chosen to illustrate the different phases of evolution. At each time, offset on the vertical axis for clarity with times listed in units of
$\times$
’ markers in panel (a), which are chosen to illustrate the different phases of evolution. At each time, offset on the vertical axis for clarity with times listed in units of
![]() $\unicode[STIX]{x03A9}^{-1}$
, we show
$\unicode[STIX]{x03A9}^{-1}$
, we show
![]() $\unicode[STIX]{x1D6FF}B_{x}/\max (\unicode[STIX]{x1D6FF}B)$
with solid lines,
$\unicode[STIX]{x1D6FF}B_{x}/\max (\unicode[STIX]{x1D6FF}B)$
with solid lines,
![]() $\unicode[STIX]{x1D6FF}B_{y}/\max (\unicode[STIX]{x1D6FF}B)$
with dashed lines, and
$\unicode[STIX]{x1D6FF}B_{y}/\max (\unicode[STIX]{x1D6FF}B)$
with dashed lines, and
![]() $\unicode[STIX]{x0394}p/\max (|\unicode[STIX]{x0394}p|)$
with dotted lines (the grey lines show
$\unicode[STIX]{x0394}p/\max (|\unicode[STIX]{x0394}p|)$
with dotted lines (the grey lines show
![]() $0$
to more clearly separate each curve). The mode transitions (around
$0$
to more clearly separate each curve). The mode transitions (around
![]() $t\approx 16~\unicode[STIX]{x03A9}^{-1}$
) from structures characteristic of the azimuthal-field KMRI with
$t\approx 16~\unicode[STIX]{x03A9}^{-1}$
) from structures characteristic of the azimuthal-field KMRI with
![]() $\unicode[STIX]{x0394}p$
both positive and negative, to those characteristic of the MHD-like vertical-field MRI, with the pressure anisotropy everywhere positive and at the mirror limit. Although less clean than the single-mode case studied in figure 2, the structures at very late times (
$\unicode[STIX]{x0394}p$
both positive and negative, to those characteristic of the MHD-like vertical-field MRI, with the pressure anisotropy everywhere positive and at the mirror limit. Although less clean than the single-mode case studied in figure 2, the structures at very late times (
![]() $t=24$
) are again affected by compressibility in the same way (cf.,
$t=24$
) are again affected by compressibility in the same way (cf.,
![]() $\unicode[STIX]{x1D6FF}B_{x}$
and
$\unicode[STIX]{x1D6FF}B_{x}$
and
![]() $\unicode[STIX]{x1D6FF}B_{y}$
with those shown in figure 2
d).
$\unicode[STIX]{x1D6FF}B_{y}$
with those shown in figure 2
d).
3.3 Nonlinear KMRI: azimuthal–vertical magnetic field
In this section, we consider the effect of an additional background azimuthal magnetic field. We focus mainly on the collisionless KMRI (LF model; § 3.3.1), briefly mentioning the Braginskii version (for which the conclusions are similar) in § 3.3.2. As shown in figure 1, the MRI (or MVI) under such conditions is significantly different from the vertical background field case, growing fastest at long wavelengths
![]() $k_{\text{max}}v_{Az}/\unicode[STIX]{x1D6FA}\ll 1$
with growth rates exceeding
$k_{\text{max}}v_{Az}/\unicode[STIX]{x1D6FA}\ll 1$
with growth rates exceeding
![]() $S/2$
. This situation is arguably more relevant astrophysically than is the pure vertical-field case: at high
$S/2$
. This situation is arguably more relevant astrophysically than is the pure vertical-field case: at high
![]() $\unicode[STIX]{x1D6FD}_{0}$
, even small azimuthal fields significantly modify the dispersion relation (see appendix A).
$\unicode[STIX]{x1D6FD}_{0}$
, even small azimuthal fields significantly modify the dispersion relation (see appendix A).
3.3.1 Collisionless (LF) regime
As with the vertical-field KMRI, nonlinear effects become important in the collisionless case at very low amplitudes, specifically when
![]() $\unicode[STIX]{x1D6FF}B_{y}\sim \unicode[STIX]{x1D6FD}_{0}^{-2/3}B_{0}$
(or when
$\unicode[STIX]{x1D6FF}B_{y}\sim \unicode[STIX]{x1D6FD}_{0}^{-2/3}B_{0}$
(or when
![]() $\unicode[STIX]{x1D6FF}B_{x}\sim \unicode[STIX]{x1D6FD}_{0}^{-1/3}B_{0}$
, see (A 4)–(A 7)). Once the perturbed field becomes larger than the background field, the magnetic field is dominated by the mode itself and the instability again becomes similar to the MHD MRI (or, equivalently, the vertical-field KMRI at large amplitudes).
$\unicode[STIX]{x1D6FF}B_{x}\sim \unicode[STIX]{x1D6FD}_{0}^{-1/3}B_{0}$
, see (A 4)–(A 7)). Once the perturbed field becomes larger than the background field, the magnetic field is dominated by the mode itself and the instability again becomes similar to the MHD MRI (or, equivalently, the vertical-field KMRI at large amplitudes).
We now describe how such a mode transitions through four distinct stages in its nonlinear evolution, which is illustrated schematically in figure 3. Let us consider each stage of evolution separately, assuming
![]() $B_{0y}\approx B_{0z}=B_{0}/\sqrt{2}$
for the sake of simplicity:
$B_{0y}\approx B_{0z}=B_{0}/\sqrt{2}$
for the sake of simplicity:
(1) Linear evolution. Unlike in the vertical-field case, the KMRI mode linearly produces a pressure anisotropy,
because
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{B}_{0}=\unicode[STIX]{x1D6FF}B_{y}B_{0y}\neq 0$
(here we have set
$\unicode[STIX]{x1D6FF}\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{B}_{0}=\unicode[STIX]{x1D6FF}B_{y}B_{0y}\neq 0$
(here we have set
![]() $B_{0y}\approx B_{0z}$
; see Reference Quataert, Dorland and HammettQ02 and appendix A). This implies that, as the mode evolves, it pushes the plasma towards both the mirror limit, in regions where
$B_{0y}\approx B_{0z}$
; see Reference Quataert, Dorland and HammettQ02 and appendix A). This implies that, as the mode evolves, it pushes the plasma towards both the mirror limit, in regions where
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{B}_{0}>0$
(i.e.
$\unicode[STIX]{x1D6FF}\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{B}_{0}>0$
(i.e.
![]() $\unicode[STIX]{x1D6FF}B_{y}B_{0y}>0$
), and the firehose limit, in regions where
$\unicode[STIX]{x1D6FF}B_{y}B_{0y}>0$
), and the firehose limit, in regions where
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{B}_{0}<0$
(
$\unicode[STIX]{x1D6FF}\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{B}_{0}<0$
(
![]() $\unicode[STIX]{x1D6FF}B_{y}B_{0y}<0$
). Note that the factor
$\unicode[STIX]{x1D6FF}B_{y}B_{0y}<0$
). Note that the factor
![]() $\unicode[STIX]{x1D6FE}/(c_{s}k)^{-1}\sim \unicode[STIX]{x1D6FD}_{0}^{-1/2}(v_{A}k/\unicode[STIX]{x1D6FE})^{-1}$
in (3.6) arises due to the smoothing effect of the heat fluxes and reduces
$\unicode[STIX]{x1D6FE}/(c_{s}k)^{-1}\sim \unicode[STIX]{x1D6FD}_{0}^{-1/2}(v_{A}k/\unicode[STIX]{x1D6FE})^{-1}$
in (3.6) arises due to the smoothing effect of the heat fluxes and reduces
![]() $\unicode[STIX]{x1D6E5}$
significantly (for example, in the CGL model where
$\unicode[STIX]{x1D6E5}$
significantly (for example, in the CGL model where
![]() $q_{\bot }=q_{\Vert }=0$
,
$q_{\bot }=q_{\Vert }=0$
,
![]() $\unicode[STIX]{x1D6E5}\approx 3\unicode[STIX]{x1D6FF}B_{y}/B_{0}$
is much larger than (3.6)). The linear phase ends as
$\unicode[STIX]{x1D6E5}\approx 3\unicode[STIX]{x1D6FF}B_{y}/B_{0}$
is much larger than (3.6)). The linear phase ends as
![]() $\unicode[STIX]{x1D6E5}$
approaches the microinstability limits
$\unicode[STIX]{x1D6E5}$
approaches the microinstability limits
![]() $|\unicode[STIX]{x1D6E5}|\sim \unicode[STIX]{x1D6FD}^{-1}$
and becomes flattened by growing mirror and firehose fluctuations. Assuming the mode grows at the scale that maximizes the growth rate,
$|\unicode[STIX]{x1D6E5}|\sim \unicode[STIX]{x1D6FD}^{-1}$
and becomes flattened by growing mirror and firehose fluctuations. Assuming the mode grows at the scale that maximizes the growth rate,
![]() $k_{\text{max}}v_{A}/\unicode[STIX]{x1D6FA}\sim \unicode[STIX]{x1D6FD}_{0}^{-1/6}$
(see (A 2) and figure 7), these limits are reached when
$k_{\text{max}}v_{A}/\unicode[STIX]{x1D6FA}\sim \unicode[STIX]{x1D6FD}_{0}^{-1/6}$
(see (A 2) and figure 7), these limits are reached when
![]() $\unicode[STIX]{x1D6FF}B_{y}\sim \unicode[STIX]{x1D6FD}^{-2/3}B_{0}$
, or when
$\unicode[STIX]{x1D6FF}B_{y}\sim \unicode[STIX]{x1D6FD}^{-2/3}B_{0}$
, or when
![]() $\unicode[STIX]{x1D6FF}B_{x}\sim \unicode[STIX]{x1D6FD}^{-1/3}B_{0}$
(since
$\unicode[STIX]{x1D6FF}B_{x}\sim \unicode[STIX]{x1D6FD}^{-1/3}B_{0}$
(since
![]() $\unicode[STIX]{x1D6FF}B_{x}\sim \unicode[STIX]{x1D6FD}_{0}^{1/3}\unicode[STIX]{x1D6FF}B_{y}$
for these fastest-growing modes; see (A 4)–(A 7)). At this point, the perturbation of
$\unicode[STIX]{x1D6FF}B_{x}\sim \unicode[STIX]{x1D6FD}_{0}^{1/3}\unicode[STIX]{x1D6FF}B_{y}$
for these fastest-growing modes; see (A 4)–(A 7)). At this point, the perturbation of
![]() $B$
due to
$B$
due to
![]() $\unicode[STIX]{x1D6FF}B_{x}$
is similar to that due to
$\unicode[STIX]{x1D6FF}B_{x}$
is similar to that due to
![]() $\unicode[STIX]{x1D6FF}B_{y}$
, meaning that both components contribute to the pressure anisotropy.Footnote
7
$\unicode[STIX]{x1D6FF}B_{y}$
, meaning that both components contribute to the pressure anisotropy.Footnote
7
(2) Pressure anisotropy limited, with
![]() $\unicode[STIX]{x1D6FF}B_{y}<B_{0y}$
. In the limit that the mirror and firehose fluctuations efficiently constrain the growing
$\unicode[STIX]{x1D6FF}B_{y}<B_{0y}$
. In the limit that the mirror and firehose fluctuations efficiently constrain the growing
![]() $|\unicode[STIX]{x1D6E5}|$
, the pressure profile will develop a step function profile in space between the mirror limit,
$|\unicode[STIX]{x1D6E5}|$
, the pressure profile will develop a step function profile in space between the mirror limit,
![]() $\unicode[STIX]{x1D6E5}\approx 1/\unicode[STIX]{x1D6FD}$
, and the firehose limit
$\unicode[STIX]{x1D6E5}\approx 1/\unicode[STIX]{x1D6FD}$
, and the firehose limit
![]() $\unicode[STIX]{x1D6E5}\approx -2/\unicode[STIX]{x1D6FD}$
(see figure 3
b at
$\unicode[STIX]{x1D6E5}\approx -2/\unicode[STIX]{x1D6FD}$
(see figure 3
b at
![]() $t=12.5~\unicode[STIX]{x03A9}^{-1}$
). A key effect of these limits is that they suppress the influence of the
$t=12.5~\unicode[STIX]{x03A9}^{-1}$
). A key effect of these limits is that they suppress the influence of the
![]() $\unicode[STIX]{x1D6FF}p_{\bot }$
and
$\unicode[STIX]{x1D6FF}p_{\bot }$
and
![]() $\unicode[STIX]{x1D6FF}p_{\Vert }$
perturbations on the mode evolution. Without such pressure perturbations, the MRI reverts back to standard, MHD-like behaviour characteristic of the vertical-field MRI (this can be seen, for example, by artificially suppressing
$\unicode[STIX]{x1D6FF}p_{\Vert }$
perturbations on the mode evolution. Without such pressure perturbations, the MRI reverts back to standard, MHD-like behaviour characteristic of the vertical-field MRI (this can be seen, for example, by artificially suppressing
![]() $\unicode[STIX]{x1D6FF}p_{\bot ,\Vert }$
perturbations in a calculation of the
$\unicode[STIX]{x1D6FF}p_{\bot ,\Vert }$
perturbations in a calculation of the
![]() $B_{0y}\neq 0$
KMRI dispersion relation). Specifically, the growth rate approaches zero for
$B_{0y}\neq 0$
KMRI dispersion relation). Specifically, the growth rate approaches zero for
![]() $kv_{A}\lesssim \unicode[STIX]{x1D6FA}$
and peaks at smaller scales
$kv_{A}\lesssim \unicode[STIX]{x1D6FA}$
and peaks at smaller scales
![]() $kv_{A}\sim \unicode[STIX]{x1D6FA}$
. Thus, the long-wavelength linear modes are significantly stabilized (i.e.
$kv_{A}\sim \unicode[STIX]{x1D6FA}$
. Thus, the long-wavelength linear modes are significantly stabilized (i.e.
![]() $\unicode[STIX]{x1D6FE}$
at low
$\unicode[STIX]{x1D6FE}$
at low
![]() $k$
is small) and the mode moves to shorter wavelengths. Such behaviour is expected intuitively because the azimuthal pressure force, which is the cause of the enhanced low-
$k$
is small) and the mode moves to shorter wavelengths. Such behaviour is expected intuitively because the azimuthal pressure force, which is the cause of the enhanced low-
![]() $k$
linear growth rate (Reference Quataert, Dorland and HammettQ02; Balbus Reference Balbus2004), is limited by the mirror and firehose fluctuations. Because the standard MRI grows with the perturbed energies in approximate equipartition,
$k$
linear growth rate (Reference Quataert, Dorland and HammettQ02; Balbus Reference Balbus2004), is limited by the mirror and firehose fluctuations. Because the standard MRI grows with the perturbed energies in approximate equipartition,
![]() $\unicode[STIX]{x1D6FF}B_{y}$
must ‘catch up’ to
$\unicode[STIX]{x1D6FF}B_{y}$
must ‘catch up’ to
![]() $\unicode[STIX]{x1D6FF}B_{x}$
, and both of these must catch up to the velocity perturbations (which grow linearly with
$\unicode[STIX]{x1D6FF}B_{x}$
, and both of these must catch up to the velocity perturbations (which grow linearly with
![]() $\unicode[STIX]{x1D6FF}u_{x}\sim \unicode[STIX]{x1D6FF}u_{y}\sim \unicode[STIX]{x1D6FD}_{0}^{1/2}\unicode[STIX]{x1D6FF}B_{y}$
) during this phase of evolution (in other words,
$\unicode[STIX]{x1D6FF}u_{x}\sim \unicode[STIX]{x1D6FF}u_{y}\sim \unicode[STIX]{x1D6FD}_{0}^{1/2}\unicode[STIX]{x1D6FF}B_{y}$
) during this phase of evolution (in other words,
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{u}$
grows more slowly than
$\unicode[STIX]{x1D6FF}\boldsymbol{u}$
grows more slowly than
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{B}$
). This picture is confirmed by 1-D numerical calculations, with the growth of
$\unicode[STIX]{x1D6FF}\boldsymbol{B}$
). This picture is confirmed by 1-D numerical calculations, with the growth of
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{u}$
decreasing significantly as shorter wavelengths take over; see figure 3(a), Region 2. We also see smaller-scale perturbations growing on top of the longer-wavelength mode in figure 3(b) at
$\unicode[STIX]{x1D6FF}\boldsymbol{u}$
decreasing significantly as shorter wavelengths take over; see figure 3(a), Region 2. We also see smaller-scale perturbations growing on top of the longer-wavelength mode in figure 3(b) at
![]() $t\unicode[STIX]{x1D6FA}=12.5$
(e.g. around
$t\unicode[STIX]{x1D6FA}=12.5$
(e.g. around
![]() $z=0.2$
and
$z=0.2$
and
![]() $z=0.85$
), particularly in those regions at the firehose limit where the MRI preferentially grows at smaller scales because
$z=0.85$
), particularly in those regions at the firehose limit where the MRI preferentially grows at smaller scales because
![]() $\unicode[STIX]{x0394}p<0$
. Note that the mode cannot be stabilized completely during this phase because the MRI growth rate on a background
$\unicode[STIX]{x0394}p<0$
. Note that the mode cannot be stabilized completely during this phase because the MRI growth rate on a background
![]() $\unicode[STIX]{x0394}p$
, though small, is non-zero as
$\unicode[STIX]{x0394}p$
, though small, is non-zero as
![]() $k\rightarrow 0$
.
$k\rightarrow 0$
.
3.
![]() $\unicode[STIX]{x1D6FF}B_{y}>B_{0y}$
. As the amplitude of
$\unicode[STIX]{x1D6FF}B_{y}>B_{0y}$
. As the amplitude of
![]() $\unicode[STIX]{x1D6FF}B$
grows larger than the background
$\unicode[STIX]{x1D6FF}B$
grows larger than the background
![]() $B_{0y}$
field, the mode enters a second phase of nonlinear evolution. With the field-line direction dominated by the perturbation, the presence of a background
$B_{0y}$
field, the mode enters a second phase of nonlinear evolution. With the field-line direction dominated by the perturbation, the presence of a background
![]() $B_{0y}$
loses its dynamical importance and the mode behaves similarly to the vertical-field case, growing at
$B_{0y}$
loses its dynamical importance and the mode behaves similarly to the vertical-field case, growing at
![]() $kv_{A}\sim \unicode[STIX]{x1D6FA}$
. In addition, because the magnitude of the magnetic field is now growing everywhere in space,
$kv_{A}\sim \unicode[STIX]{x1D6FA}$
. In addition, because the magnitude of the magnetic field is now growing everywhere in space,
![]() $\unicode[STIX]{x1D6E5}$
becomes everywhere positive and will be limited only by the mirror instability; see figure 3(b) at
$\unicode[STIX]{x1D6E5}$
becomes everywhere positive and will be limited only by the mirror instability; see figure 3(b) at
![]() $t=21~\unicode[STIX]{x03A9}^{-1}$
. As with the vertical-field MRI, when the perturbation amplitude dominates the total
$t=21~\unicode[STIX]{x03A9}^{-1}$
. As with the vertical-field MRI, when the perturbation amplitude dominates the total
![]() $B$
, the pressure anisotropy
$B$
, the pressure anisotropy
![]() $\unicode[STIX]{x0394}p\approx (\unicode[STIX]{x1D6FF}B_{x}^{2}+\unicode[STIX]{x1D6FF}B_{y}^{2})/8\unicode[STIX]{x03C0}$
does not cause significant nonlinear modifications, because
$\unicode[STIX]{x0394}p\approx (\unicode[STIX]{x1D6FF}B_{x}^{2}+\unicode[STIX]{x1D6FF}B_{y}^{2})/8\unicode[STIX]{x03C0}$
does not cause significant nonlinear modifications, because
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FF}\boldsymbol{B}=0$
for an MRI channel mode.
$\unicode[STIX]{x1D6FF}\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FF}\boldsymbol{B}=0$
for an MRI channel mode.
4. Compressibility effects. There is no 1-D mechanism to halt the growth of the mode until
![]() $\unicode[STIX]{x1D6FF}u$
approaches the sound speed (
$\unicode[STIX]{x1D6FF}u$
approaches the sound speed (
![]() $\unicode[STIX]{x1D6FF}B_{x}\sim \unicode[STIX]{x1D6FF}B_{y}\sim \unicode[STIX]{x1D6FD}^{1/2}B_{0}$
). Thus, the mode behaves similarly to the vertical-field MRI, with large variations in
$\unicode[STIX]{x1D6FF}B_{x}\sim \unicode[STIX]{x1D6FF}B_{y}\sim \unicode[STIX]{x1D6FD}^{1/2}B_{0}$
). Thus, the mode behaves similarly to the vertical-field MRI, with large variations in
![]() $\unicode[STIX]{x1D70C}$
. The profiles that develop have the same characteristic shape as those seen in figure 2(d) (cf., figure 3
b at
$\unicode[STIX]{x1D70C}$
. The profiles that develop have the same characteristic shape as those seen in figure 2(d) (cf., figure 3
b at
![]() $t\unicode[STIX]{x1D6FA}=24$
).
$t\unicode[STIX]{x1D6FA}=24$
).
Each of the four stages discussed above can be seen in the mode energy evolution, shown in figure 3(a). In contrast to the calculation of the vertical-field MRI evolution (figure 2), we begin from random large-scale initial conditions at much higher
![]() $\unicode[STIX]{x1D6FD}_{0}=5000$
(with
$\unicode[STIX]{x1D6FD}_{0}=5000$
(with
![]() $B_{0y}=B_{0z}$
), so as to clearly distinguish between the different regions of evolution and allow the smaller scale modes to grow after
$B_{0y}=B_{0z}$
), so as to clearly distinguish between the different regions of evolution and allow the smaller scale modes to grow after
![]() $\unicode[STIX]{x1D6E5}$
reaches the microinstability limits. While the details of the process described above will be modified depending on a variety of factors – e.g. the mode wavelength in comparison to the domain, the spectrum of the initial conditions, and the value of
$\unicode[STIX]{x1D6E5}$
reaches the microinstability limits. While the details of the process described above will be modified depending on a variety of factors – e.g. the mode wavelength in comparison to the domain, the spectrum of the initial conditions, and the value of
![]() $B_{0y}/B_{0z}$
– the basic concepts and phases of evolution should be generally applicable. It is also worth noting that, at the large values of
$B_{0y}/B_{0z}$
– the basic concepts and phases of evolution should be generally applicable. It is also worth noting that, at the large values of
![]() $\unicode[STIX]{x1D6FD}$
for which our arguments are most applicable, the mode will likely collapse into turbulence before the final nonlinear stage where compressibility is important (see § 4).
$\unicode[STIX]{x1D6FD}$
for which our arguments are most applicable, the mode will likely collapse into turbulence before the final nonlinear stage where compressibility is important (see § 4).
3.3.2 Weakly collisional (Braginskii) regime
As with the vertical-field MRI in the Braginskii regime (§ 3.2.2), there are two different Braginskii sub-regimes: (i) if
![]() $\overline{\unicode[STIX]{x1D708}}_{c}\equiv \unicode[STIX]{x1D708}_{c}/S\ll \unicode[STIX]{x1D6FD}^{1/2}$
, the instability grows at a similar rate to the collisionless instability (and the heat fluxes play an important dynamical role), or (ii) if
$\overline{\unicode[STIX]{x1D708}}_{c}\equiv \unicode[STIX]{x1D708}_{c}/S\ll \unicode[STIX]{x1D6FD}^{1/2}$
, the instability grows at a similar rate to the collisionless instability (and the heat fluxes play an important dynamical role), or (ii) if
![]() $\overline{\unicode[STIX]{x1D708}}_{c}~\gg \unicode[STIX]{x1D6FD}^{1/2}$
, the growth rate of the MVI is reduced, reaching the collisional (standard MHD) regime when
$\overline{\unicode[STIX]{x1D708}}_{c}~\gg \unicode[STIX]{x1D6FD}^{1/2}$
, the growth rate of the MVI is reduced, reaching the collisional (standard MHD) regime when
![]() $\overline{\unicode[STIX]{x1D708}}_{c}\sim \unicode[STIX]{x1D6FD}$
(see figures 1–3 of Sharma et al.
Reference Sharma, Hammett and Quataert2003). To understand this latter point – that the Braginskii MRI becomes MHD-like when
$\overline{\unicode[STIX]{x1D708}}_{c}\sim \unicode[STIX]{x1D6FD}$
(see figures 1–3 of Sharma et al.
Reference Sharma, Hammett and Quataert2003). To understand this latter point – that the Braginskii MRI becomes MHD-like when
![]() $\overline{\unicode[STIX]{x1D708}}_{c}\gtrsim \unicode[STIX]{x1D6FD}$
– we compare the Lorentz force,
$\overline{\unicode[STIX]{x1D708}}_{c}\gtrsim \unicode[STIX]{x1D6FD}$
– we compare the Lorentz force,
![]() $\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FF}\boldsymbol{B}=\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\boldsymbol{B}_{0}\unicode[STIX]{x1D6FF}\boldsymbol{B})$
, to the pressure-anisotropy force
$\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FF}\boldsymbol{B}=\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\boldsymbol{B}_{0}\unicode[STIX]{x1D6FF}\boldsymbol{B})$
, to the pressure-anisotropy force
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\hat{\boldsymbol{b}}\hat{\boldsymbol{b}}\unicode[STIX]{x0394}p)$
that arises from the (linear)
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\hat{\boldsymbol{b}}\hat{\boldsymbol{b}}\unicode[STIX]{x0394}p)$
that arises from the (linear)
![]() $\unicode[STIX]{x0394}p$
induced by the KMRI mode,
$\unicode[STIX]{x0394}p$
induced by the KMRI mode,
where
![]() $B_{0}^{2}=B_{0y}^{2}+B_{0z}^{2}$
and we have assumed
$B_{0}^{2}=B_{0y}^{2}+B_{0z}^{2}$
and we have assumed
![]() $B_{0y}\sim B_{0z}$
. Note that we have neglected the heat fluxes in (3.7), which act to reduce
$B_{0y}\sim B_{0z}$
. Note that we have neglected the heat fluxes in (3.7), which act to reduce
![]() $\unicode[STIX]{x0394}p$
(see (3.6)), as is appropriate for the high-collisionality regime (see § B.4). We see from (3.7) that the pressure-anisotropy stress is larger than the Lorentz force (and thus important for the mode’s evolution) only if
$\unicode[STIX]{x0394}p$
(see (3.6)), as is appropriate for the high-collisionality regime (see § B.4). We see from (3.7) that the pressure-anisotropy stress is larger than the Lorentz force (and thus important for the mode’s evolution) only if
![]() $\overline{\unicode[STIX]{x1D708}}_{c}\lesssim \unicode[STIX]{x1D6FD}$
, as expected (Sharma et al.
Reference Sharma, Hammett and Quataert2003).
$\overline{\unicode[STIX]{x1D708}}_{c}\lesssim \unicode[STIX]{x1D6FD}$
, as expected (Sharma et al.
Reference Sharma, Hammett and Quataert2003).
Numerical experiments (not shown) have revealed that, in the moderate-collisionality regime
![]() $\overline{\unicode[STIX]{x1D708}}_{c}\equiv \unicode[STIX]{x1D708}_{c}/S\ll \unicode[STIX]{x1D6FD}^{1/2}$
, the Braginskii KMRI behaves similarly to a truly collisionless mode (this should be expected based on the arguments above and in § 3.2.2). As described in § 3.2.2, at very large amplitudes,
$\overline{\unicode[STIX]{x1D708}}_{c}\equiv \unicode[STIX]{x1D708}_{c}/S\ll \unicode[STIX]{x1D6FD}^{1/2}$
, the Braginskii KMRI behaves similarly to a truly collisionless mode (this should be expected based on the arguments above and in § 3.2.2). As described in § 3.2.2, at very large amplitudes,
![]() $\unicode[STIX]{x1D6FF}B>B_{0}$
(Region 3), the evolution differs from a collisionless mode once
$\unicode[STIX]{x1D6FF}B>B_{0}$
(Region 3), the evolution differs from a collisionless mode once
![]() $\unicode[STIX]{x1D6FF}B\gtrsim (\unicode[STIX]{x1D6FD}_{0}/\overline{\unicode[STIX]{x1D708}}_{c})^{1/2}B_{0}$
(the growing mode can no longer sustain
$\unicode[STIX]{x1D6FF}B\gtrsim (\unicode[STIX]{x1D6FD}_{0}/\overline{\unicode[STIX]{x1D708}}_{c})^{1/2}B_{0}$
(the growing mode can no longer sustain
![]() $\unicode[STIX]{x0394}p$
at the mirror limit). In the high-collisionality regime,
$\unicode[STIX]{x0394}p$
at the mirror limit). In the high-collisionality regime,
![]() $\overline{\unicode[STIX]{x1D708}}_{c}\gtrsim \unicode[STIX]{x1D6FD}^{1/2}$
, the linear mode itself transitions back to the standard MHD MRI, and much of the discussion above loses its relevance. In particular, the most-unstable mode moves to larger scales as
$\overline{\unicode[STIX]{x1D708}}_{c}\gtrsim \unicode[STIX]{x1D6FD}^{1/2}$
, the linear mode itself transitions back to the standard MHD MRI, and much of the discussion above loses its relevance. In particular, the most-unstable mode moves to larger scales as
![]() $\overline{\unicode[STIX]{x1D708}}_{c}$
increases (see figure 2b of Sharma et al.
Reference Sharma, Hammett and Quataert2003). This implies that the sudden reduction in the scale of the mode when
$\overline{\unicode[STIX]{x1D708}}_{c}$
increases (see figure 2b of Sharma et al.
Reference Sharma, Hammett and Quataert2003). This implies that the sudden reduction in the scale of the mode when
![]() $\unicode[STIX]{x0394}p\sim B^{2}$
(see figure 3
b between
$\unicode[STIX]{x0394}p\sim B^{2}$
(see figure 3
b between
![]() $t\approx 12.5$
and
$t\approx 12.5$
and
![]() $t\approx 21$
) is much less relevant. The mode causes
$t\approx 21$
) is much less relevant. The mode causes
![]() $\unicode[STIX]{x0394}p$
to reach the mirror and firehose limit at some amplitude
$\unicode[STIX]{x0394}p$
to reach the mirror and firehose limit at some amplitude
![]() $\unicode[STIX]{x1D6FF}B\lesssim B_{0}$
(with the exact point depending on
$\unicode[STIX]{x1D6FF}B\lesssim B_{0}$
(with the exact point depending on
![]() $\overline{\unicode[STIX]{x1D708}}_{c}/\unicode[STIX]{x1D6FD}$
) and then transition to the behaviour discussed in § 3.2.2 once
$\overline{\unicode[STIX]{x1D708}}_{c}/\unicode[STIX]{x1D6FD}$
) and then transition to the behaviour discussed in § 3.2.2 once
![]() $\unicode[STIX]{x1D6FF}B\gtrsim B_{0}$
.
$\unicode[STIX]{x1D6FF}B\gtrsim B_{0}$
.
3.4 General discussion of 1-D nonlinearities
With the diverse assortment of nonlinear effects outlined in the previous sections, it seems prudent to conclude with a discussion of some overarching ideas. As is generally the case in high-
![]() $\unicode[STIX]{x1D6FD}$
collisionless plasma dynamics (e.g. Schekochihin & Cowley Reference Schekochihin and Cowley2006; Squire et al.
Reference Squire, Quataert and Schekochihin2016), nonlinearity can be important for perturbation amplitudes far below what one might naively expect. For the MRI in the collisionless regime, this occurs a factor of
$\unicode[STIX]{x1D6FD}$
collisionless plasma dynamics (e.g. Schekochihin & Cowley Reference Schekochihin and Cowley2006; Squire et al.
Reference Squire, Quataert and Schekochihin2016), nonlinearity can be important for perturbation amplitudes far below what one might naively expect. For the MRI in the collisionless regime, this occurs a factor of
![]() ${\sim}\unicode[STIX]{x1D6FD}_{0}$
(or
${\sim}\unicode[STIX]{x1D6FD}_{0}$
(or
![]() ${\sim}\unicode[STIX]{x1D6FD}_{0}^{7/6}$
for
${\sim}\unicode[STIX]{x1D6FD}_{0}^{7/6}$
for
![]() $\unicode[STIX]{x1D6FF}B_{y}$
with
$\unicode[STIX]{x1D6FF}B_{y}$
with
![]() $B_{0y}\neq 0$
) below where nonlinear effects become important in standard MHD. However, we have also seen that, in all cases considered, the KMRI (or MVI) always reverts to MHD-like evolution at large amplitudes due to the anisotropy-limiting response of the mirror and firehose instabilities (e.g. Kunz et al.
Reference Kunz, Schekochihin and Stone2014a
). This behaviour has also been seen in fully kinetic 2-D simulations (Riquelme et al.
Reference Riquelme, Quataert, Sharma and Spitkovsky2012). More specifically, this arises because of the form of the pressure anisotropy, viz.
$B_{0y}\neq 0$
) below where nonlinear effects become important in standard MHD. However, we have also seen that, in all cases considered, the KMRI (or MVI) always reverts to MHD-like evolution at large amplitudes due to the anisotropy-limiting response of the mirror and firehose instabilities (e.g. Kunz et al.
Reference Kunz, Schekochihin and Stone2014a
). This behaviour has also been seen in fully kinetic 2-D simulations (Riquelme et al.
Reference Riquelme, Quataert, Sharma and Spitkovsky2012). More specifically, this arises because of the form of the pressure anisotropy, viz.
![]() $\unicode[STIX]{x0394}p=B^{2}/8\unicode[STIX]{x03C0}$
, when it is limited at the mirror threshold. If
$\unicode[STIX]{x0394}p=B^{2}/8\unicode[STIX]{x03C0}$
, when it is limited at the mirror threshold. If
![]() $B$
is dominated by the mode itself (
$B$
is dominated by the mode itself (
![]() $B^{2}\approx \unicode[STIX]{x1D6FF}B^{2}$
), then the anisotropic stress in the momentum equation (2.2),
$B^{2}\approx \unicode[STIX]{x1D6FF}B^{2}$
), then the anisotropic stress in the momentum equation (2.2),
acts like an additional Lorentz force, which is zero for the MRI channel mode (Goodman & Xu Reference Goodman and Xu1994). This implies that the pressure-anisotropy effects that are critical to the difference between the KMRI and the MRI in linear theory become unimportant once
![]() $\unicode[STIX]{x1D6FF}B\gtrsim B_{0}$
. Due to this, a large-amplitude collisionless KMRI channel mode is an approximate nonlinear solution (of the LF equations), as in MHD, until its amplitude approaches the sound speed (there is a minor complication in the Braginskii regime; see § 3.2.2). Thus, the effect of compressibility on the large-amplitude mode structure – if this occurs before breakdown into turbulence – looks nearly identical in the MHD and kinetic models, with either a Braginskii or LF closure, and with or without azimuthal fields (this structure is shown in figure 2
d). Very similar structures are also seen at large amplitudes in fully kinetic simulations (Kunz et al.
Reference Kunz, Stone and Bai2014b
).
$\unicode[STIX]{x1D6FF}B\gtrsim B_{0}$
. Due to this, a large-amplitude collisionless KMRI channel mode is an approximate nonlinear solution (of the LF equations), as in MHD, until its amplitude approaches the sound speed (there is a minor complication in the Braginskii regime; see § 3.2.2). Thus, the effect of compressibility on the large-amplitude mode structure – if this occurs before breakdown into turbulence – looks nearly identical in the MHD and kinetic models, with either a Braginskii or LF closure, and with or without azimuthal fields (this structure is shown in figure 2
d). Very similar structures are also seen at large amplitudes in fully kinetic simulations (Kunz et al.
Reference Kunz, Stone and Bai2014b
).
In contrast, the effect of the nonlinearity at intermediate amplitudes
![]() $\unicode[STIX]{x1D6FF}B\lesssim B_{0}$
differs between plasma regimes (collisionless and Braginskii) and background field configurations. For modes growing in a purely vertical background field, the nonlinear modification of the mode is modest, so long as the mirror fluctuations limit
$\unicode[STIX]{x1D6FF}B\lesssim B_{0}$
differs between plasma regimes (collisionless and Braginskii) and background field configurations. For modes growing in a purely vertical background field, the nonlinear modification of the mode is modest, so long as the mirror fluctuations limit
![]() $\unicode[STIX]{x1D6E5}$
to be close to
$\unicode[STIX]{x1D6E5}$
to be close to
![]() $1/\unicode[STIX]{x1D6FD}$
. However, even moderate overshoot past the mirror limit – for example, as might occur in numerical simulations due to insufficient scale separation between
$1/\unicode[STIX]{x1D6FD}$
. However, even moderate overshoot past the mirror limit – for example, as might occur in numerical simulations due to insufficient scale separation between
![]() $\unicode[STIX]{x1D6FA}_{i}$
and
$\unicode[STIX]{x1D6FA}_{i}$
and
![]() $\unicode[STIX]{x1D6FA}$
, see § 6 – can cause quite strong modifications and/or cause the mode to move to longer wavelengths. Modes evolving in a mixed-vertical–azimuthal background field behave very differently, because the pressure perturbation participates directly in the linear instability (Reference Quataert, Dorland and HammettQ02). Upon reaching the mirror and firehose microinstability limits, the pressure perturbation can no longer contribute to the linear growth and the mode moves towards the smaller scales characteristic of the standard MRI once
$\unicode[STIX]{x1D6FA}$
, see § 6 – can cause quite strong modifications and/or cause the mode to move to longer wavelengths. Modes evolving in a mixed-vertical–azimuthal background field behave very differently, because the pressure perturbation participates directly in the linear instability (Reference Quataert, Dorland and HammettQ02). Upon reaching the mirror and firehose microinstability limits, the pressure perturbation can no longer contribute to the linear growth and the mode moves towards the smaller scales characteristic of the standard MRI once
![]() $\unicode[STIX]{x1D6FF}B_{y}\gtrsim \unicode[STIX]{x1D6FD}^{-2/3}B_{0}$
(or
$\unicode[STIX]{x1D6FF}B_{y}\gtrsim \unicode[STIX]{x1D6FD}^{-2/3}B_{0}$
(or
![]() $\unicode[STIX]{x1D6FF}B_{x}\gtrsim \unicode[STIX]{x1D6FD}^{-1/3}B_{0}$
). This transition is illustrated graphically in figure 3.
$\unicode[STIX]{x1D6FF}B_{x}\gtrsim \unicode[STIX]{x1D6FD}^{-1/3}B_{0}$
). This transition is illustrated graphically in figure 3.
4 Saturation into turbulence
In the previous section we have argued that kinetic physics does not offer alternate routes for the saturation of MRI modes in one dimension. In particular, in all cases considered – purely vertical or mixed-vertical–azimuthal field, in both the Braginskii and collisionless limits – the final stages of mode evolution are similar to those seen in standard MHD, with the growing mode becoming close to a nonlinear solution (aside from the effects of compressibility). We must therefore consider alternate means for the saturation of the MRI, in particular 3-D turbulence. This conclusion is supported by the fully kinetic simulations of Riquelme et al. (Reference Riquelme, Quataert, Sharma and Spitkovsky2012) and Kunz et al. (Reference Kunz, Stone and Bai2014b ), in which the 2-D KMRI was seen to grow to very large amplitudes.
In this section, we are concerned with how a growing mode breaks up at large amplitudes into 3-D turbulence. This problem is somewhat separate from the study of the turbulent state itself (which we do not consider here), and has been studied by a variety of authors in terms of ‘parasitic modes’ (e.g. Goodman & Xu Reference Goodman and Xu1994, Latter et al. Reference Latter, Lesaffre and Balbus2009, Pessah & Goodman Reference Pessah and Goodman2009). These are 3-D secondary instabilities that feed off the large gradients in the growing MRI channel mode, acting to disrupt the mode and seed its transition into turbulence. While the relevance of parasitic modes to transport in the turbulent saturated state has been controversial (e.g. Bodo et al. Reference Bodo, Mignone, Cattaneo, Rossi and Ferrari2008, Latter et al. Reference Latter, Lesaffre and Balbus2009, Pessah & Goodman Reference Pessah and Goodman2009, Longaretti & Lesur Reference Longaretti and Lesur2010), they are nevertheless a helpful theoretical tool for understanding the initial saturation phase.
The question we address here is whether one should expect any striking differences (compared to MHD) in this initial saturation phase of the KMRI because of differences in the behaviour of parasitic modes brought about by pressure anisotropy. Our conclusion – within the limitations of the LF model (§ 2) – is that there are not significant differences. We also argue that the observations of larger transient channel amplitudes in Reference Sharma, Hammett, Quataert and StoneS06 are explained through the modes’ increase in wavelength at large amplitudes due to 1-D pressure-anisotropy nonlinearities (see § 3.2).
Because of this null result, and given the simplifications inherent to our fluid-based model, we keep our discussion brief. We do, however, reach these conclusions through two separate methods: (i) a study of the effect of a mean
![]() $\unicode[STIX]{x0394}p$
on linear parasitic-mode growth rates in a sinusoidal channel mode, and (ii) 3-D nonlinear simulations using the modified version of the Zeus code from Reference Sharma, Hammett, Quataert and StoneS06. We thus feel that the general conclusions reached here are relatively robust. That being said, due to the variety of other effects that may be present in a true collisionless kinetic plasma, as well as the strong dependence of MHD MRI turbulence on microphysics (e.g. magnetic Prandtl number; Fromang et al.
Reference Fromang, Papaloizou, Lesur and Heinemann2007, Meheut et al.
Reference Meheut, Fromang, Lesur, Joos and Longaretti2015), we do not necessarily claim that the initial stages of 3-D KMRI saturation should be similar to its MHD counterpart. Rather, our conclusion is more modest: there are no significant differences due to pressure anisotropy and heat fluxes (i.e. those kinetic effects contained within the LF model).
$\unicode[STIX]{x0394}p$
on linear parasitic-mode growth rates in a sinusoidal channel mode, and (ii) 3-D nonlinear simulations using the modified version of the Zeus code from Reference Sharma, Hammett, Quataert and StoneS06. We thus feel that the general conclusions reached here are relatively robust. That being said, due to the variety of other effects that may be present in a true collisionless kinetic plasma, as well as the strong dependence of MHD MRI turbulence on microphysics (e.g. magnetic Prandtl number; Fromang et al.
Reference Fromang, Papaloizou, Lesur and Heinemann2007, Meheut et al.
Reference Meheut, Fromang, Lesur, Joos and Longaretti2015), we do not necessarily claim that the initial stages of 3-D KMRI saturation should be similar to its MHD counterpart. Rather, our conclusion is more modest: there are no significant differences due to pressure anisotropy and heat fluxes (i.e. those kinetic effects contained within the LF model).
4.1 Linear parasitic-mode growth rates
In this section we directly calculate parasitic-mode growth rates for MRI and KMRI channel modes in a vertical background magnetic field. We do not consider a mixed-azimuthal–vertical background field configuration here primarily because the 1-D results of § 3.3 suggested that such modes are always relatively disordered when they reach large amplitudes anyway, due to their strong nonlinear disruption (from long wavelengths to short wavelengths) when
![]() $\unicode[STIX]{x1D6FF}B_{y}\sim B_{y}$
(see, e.g. figure 3
b). Thus the very idealized linear problem, based on purely sinusoidal background profiles, is presumably much less relevant for this case (we rectify this omission in the 3-D simulations below; see figure 6
b).
$\unicode[STIX]{x1D6FF}B_{y}\sim B_{y}$
(see, e.g. figure 3
b). Thus the very idealized linear problem, based on purely sinusoidal background profiles, is presumably much less relevant for this case (we rectify this omission in the 3-D simulations below; see figure 6
b).
Motivated by previous MHD studies (Goodman & Xu Reference Goodman and Xu1994; Latter et al.
Reference Latter, Lesaffre and Balbus2009, Reference Latter, Fromang and Gressel2010; Pessah & Goodman Reference Pessah and Goodman2009), we consider 3-D linear perturbations,
![]() $f(\boldsymbol{x})=f_{k_{x}k_{y}}(z)\exp (\text{i}k_{x}x+\text{i}k_{y}y)$
for
$f(\boldsymbol{x})=f_{k_{x}k_{y}}(z)\exp (\text{i}k_{x}x+\text{i}k_{y}y)$
for
![]() $f=\{\boldsymbol{u}^{\prime },\,\boldsymbol{B}^{\prime },\,\unicode[STIX]{x1D70C}^{\prime },\,p_{\bot ,\Vert }^{\prime }\}$
, evolving on top of a channel-mode background (
$f=\{\boldsymbol{u}^{\prime },\,\boldsymbol{B}^{\prime },\,\unicode[STIX]{x1D70C}^{\prime },\,p_{\bot ,\Vert }^{\prime }\}$
, evolving on top of a channel-mode background (
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{u}$
and
$\unicode[STIX]{x1D6FF}\boldsymbol{u}$
and
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{B}$
from (3.1), with
$\unicode[STIX]{x1D6FF}\boldsymbol{B}$
from (3.1), with
![]() $\unicode[STIX]{x1D6FF}B_{0}$
a free parameter). That is, we decompose the fields as
$\unicode[STIX]{x1D6FF}B_{0}$
a free parameter). That is, we decompose the fields as
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\boldsymbol{u}=-Sx\hat{\boldsymbol{y}}-\sqrt{{\displaystyle \frac{3}{5}}}{\displaystyle \frac{\unicode[STIX]{x1D6FF}B_{0}}{\sqrt{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}}}}\sin (kz)(\hat{\boldsymbol{x}}+\hat{\boldsymbol{y}})+\boldsymbol{u}^{\prime },\\ \boldsymbol{B}=B_{0}\hat{\boldsymbol{z}}-\unicode[STIX]{x1D6FF}B_{0}\cos (kz)(\hat{\boldsymbol{x}}-\hat{\boldsymbol{y}})+\boldsymbol{B}^{\prime },\\ \unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{0}+0+\unicode[STIX]{x1D70C}^{\prime },\\ p_{\bot }=p_{0}+\unicode[STIX]{x1D6FF}p_{\bot 0}+p_{\bot }^{\prime },\\ p_{\Vert }=p_{0}+\unicode[STIX]{x1D6FF}p_{\Vert 0}+p_{\Vert }^{\prime },\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\boldsymbol{u}=-Sx\hat{\boldsymbol{y}}-\sqrt{{\displaystyle \frac{3}{5}}}{\displaystyle \frac{\unicode[STIX]{x1D6FF}B_{0}}{\sqrt{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}}}}\sin (kz)(\hat{\boldsymbol{x}}+\hat{\boldsymbol{y}})+\boldsymbol{u}^{\prime },\\ \boldsymbol{B}=B_{0}\hat{\boldsymbol{z}}-\unicode[STIX]{x1D6FF}B_{0}\cos (kz)(\hat{\boldsymbol{x}}-\hat{\boldsymbol{y}})+\boldsymbol{B}^{\prime },\\ \unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{0}+0+\unicode[STIX]{x1D70C}^{\prime },\\ p_{\bot }=p_{0}+\unicode[STIX]{x1D6FF}p_{\bot 0}+p_{\bot }^{\prime },\\ p_{\Vert }=p_{0}+\unicode[STIX]{x1D6FF}p_{\Vert 0}+p_{\Vert }^{\prime },\end{array}\right\}\end{eqnarray}$$
with
![]() $k=2\unicode[STIX]{x03C0}/L_{z}$
, and linearize (2.1)–(2.7) in
$k=2\unicode[STIX]{x03C0}/L_{z}$
, and linearize (2.1)–(2.7) in
![]() $\boldsymbol{u}^{\prime }$
,
$\boldsymbol{u}^{\prime }$
,
![]() $\boldsymbol{B}^{\prime }$
,
$\boldsymbol{B}^{\prime }$
,
![]() $\unicode[STIX]{x1D70C}^{\prime }$
and
$\unicode[STIX]{x1D70C}^{\prime }$
and
![]() $p_{\bot ,\Vert }^{\prime }$
. (For simplicity, we ignore spatial variation in
$p_{\bot ,\Vert }^{\prime }$
. (For simplicity, we ignore spatial variation in
![]() $\unicode[STIX]{x1D6FF}p_{\bot ,\Vert 0}$
; see discussion below.) The resulting equations are solved numerically in a box with dimensionsFootnote
8
$\unicode[STIX]{x1D6FF}p_{\bot ,\Vert 0}$
; see discussion below.) The resulting equations are solved numerically in a box with dimensionsFootnote
8
![]() $(L_{x},L_{y},L_{z})=(4,4,1)$
, on a
$(L_{x},L_{y},L_{z})=(4,4,1)$
, on a
![]() $16\times 16$
grid of Fourier modes in the homogeneous
$16\times 16$
grid of Fourier modes in the homogeneous
![]() $x$
and
$x$
and
![]() $y$
directions, and with a pseudospectral method and
$y$
directions, and with a pseudospectral method and
![]() $64$
modes in the inhomogeneous
$64$
modes in the inhomogeneous
![]() $z$
direction. Hyperviscous damping is used to remove energy just above the grid scale. We initialize with random noise in all variables, and evolve in time until
$z$
direction. Hyperviscous damping is used to remove energy just above the grid scale. We initialize with random noise in all variables, and evolve in time until
![]() $t=10\unicode[STIX]{x03A9}^{-1}$
(by which time the most-unstable parasitic eigenmode mostly dominates). Fitting an exponential to the energy evolution at later times yields the growth rate
$t=10\unicode[STIX]{x03A9}^{-1}$
(by which time the most-unstable parasitic eigenmode mostly dominates). Fitting an exponential to the energy evolution at later times yields the growth rate
![]() $\unicode[STIX]{x1D6FE}$
of the least-stable parasitic mode. Intuitively, a large parasitic-mode growth rate should be associated with rapid collapse of the channel mode into MRI turbulence, because the parasitic modes will quickly ‘overtake’ the mode itself, with their 3-D structure acting as a seed for the turbulence. Further, as the MRI mode grows (i.e. as
$\unicode[STIX]{x1D6FE}$
of the least-stable parasitic mode. Intuitively, a large parasitic-mode growth rate should be associated with rapid collapse of the channel mode into MRI turbulence, because the parasitic modes will quickly ‘overtake’ the mode itself, with their 3-D structure acting as a seed for the turbulence. Further, as the MRI mode grows (i.e. as
![]() $\unicode[STIX]{x1D6FF}B_{0}$
increases) the parasitic growth rates should increase, since there are stronger gradients of
$\unicode[STIX]{x1D6FF}B_{0}$
increases) the parasitic growth rates should increase, since there are stronger gradients of
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{u}$
and
$\unicode[STIX]{x1D6FF}\boldsymbol{u}$
and
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{B}$
to feed the instabilities.
$\unicode[STIX]{x1D6FF}\boldsymbol{B}$
to feed the instabilities.
To assess the impact of the pressure anisotropy, we apply a spatially constant background pressure anisotropy
![]() $\unicode[STIX]{x0394}p_{0}=\unicode[STIX]{x1D6FF}p_{\bot 0}-\unicode[STIX]{x1D6FF}p_{\Vert 0}$
in the KMHD models and calculate the resulting change in the maximum parasitic growth rate with
$\unicode[STIX]{x0394}p_{0}=\unicode[STIX]{x1D6FF}p_{\bot 0}-\unicode[STIX]{x1D6FF}p_{\Vert 0}$
in the KMHD models and calculate the resulting change in the maximum parasitic growth rate with
![]() $\unicode[STIX]{x0394}p_{0}$
. A strong variation in growth rate with
$\unicode[STIX]{x0394}p_{0}$
. A strong variation in growth rate with
![]() $\unicode[STIX]{x0394}p_{0}$
would indicate that the saturation into turbulence is likely to depend sensitively on the self-generated pressure anisotropy, and thus differ strongly between collisional and collisionless plasmas. Of course, as discussed in § 3, there will be spatial variation in
$\unicode[STIX]{x0394}p_{0}$
would indicate that the saturation into turbulence is likely to depend sensitively on the self-generated pressure anisotropy, and thus differ strongly between collisional and collisionless plasmas. Of course, as discussed in § 3, there will be spatial variation in
![]() $\unicode[STIX]{x0394}p$
at large
$\unicode[STIX]{x0394}p$
at large
![]() $\unicode[STIX]{x1D6FF}B_{0}$
, so the study here should be considered an approximation to the full problem, considering only the simplest effects. Similarly, we neglect the influence of the background shear on the parasitic modes (this is common in previous MHD analyses), because without this simplification the resulting time dependence of
$\unicode[STIX]{x1D6FF}B_{0}$
, so the study here should be considered an approximation to the full problem, considering only the simplest effects. Similarly, we neglect the influence of the background shear on the parasitic modes (this is common in previous MHD analyses), because without this simplification the resulting time dependence of
![]() $k_{y}$
implies that an analysis in terms of eigenmodes is incorrect (one should consider transient, or non-modal, growth; Schmid Reference Schmid2007, Squire & Bhattacharjee Reference Squire and Bhattacharjee2014a
,Reference Squire and Bhattacharjee
b
). This assumption is not truly valid except at very large mode amplitudes when
$k_{y}$
implies that an analysis in terms of eigenmodes is incorrect (one should consider transient, or non-modal, growth; Schmid Reference Schmid2007, Squire & Bhattacharjee Reference Squire and Bhattacharjee2014a
,Reference Squire and Bhattacharjee
b
). This assumption is not truly valid except at very large mode amplitudes when
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{u}$
dominates strongly over the mean shear, although we expect to capture the correct qualitative trends when the parasitic growth rate is larger than the shearing rate. As mentioned above, given that the pressure anisotropy appears to cause little change to growth rates, we deliberately keep this section brief, postponing to possible future work the detailed study of the mode structure and morphology (e.g. Kelvin–Helmholtz versus tearing-mode instability) or the variation of growth rates with
$\unicode[STIX]{x1D6FF}\boldsymbol{u}$
dominates strongly over the mean shear, although we expect to capture the correct qualitative trends when the parasitic growth rate is larger than the shearing rate. As mentioned above, given that the pressure anisotropy appears to cause little change to growth rates, we deliberately keep this section brief, postponing to possible future work the detailed study of the mode structure and morphology (e.g. Kelvin–Helmholtz versus tearing-mode instability) or the variation of growth rates with
![]() $k_{x}$
and
$k_{x}$
and
![]() $k_{y}$
(Goodman & Xu Reference Goodman and Xu1994; Latter et al.
Reference Latter, Lesaffre and Balbus2009; Prajapati & Chhajlani Reference Prajapati and Chhajlani2010).
$k_{y}$
(Goodman & Xu Reference Goodman and Xu1994; Latter et al.
Reference Latter, Lesaffre and Balbus2009; Prajapati & Chhajlani Reference Prajapati and Chhajlani2010).
Figure 4. Maximum parasitic growth rates
![]() $\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D6FA}$
as a function of
$\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D6FA}$
as a function of
![]() $\unicode[STIX]{x1D6E5}=(\unicode[STIX]{x1D6FF}p_{\bot 0}-\unicode[STIX]{x1D6FF}p_{\Vert 0})/p_{0}$
for
$\unicode[STIX]{x1D6E5}=(\unicode[STIX]{x1D6FF}p_{\bot 0}-\unicode[STIX]{x1D6FF}p_{\Vert 0})/p_{0}$
for
![]() $\unicode[STIX]{x1D6FD}_{0}\approx 90$
(
$\unicode[STIX]{x1D6FD}_{0}\approx 90$
(
![]() $B_{0z}/\sqrt{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}=0.15c_{s}$
) for (a)
$B_{0z}/\sqrt{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}=0.15c_{s}$
) for (a)
![]() $\unicode[STIX]{x1D6FF}B_{0}/\sqrt{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}=0.5c_{s}\approx 3.3B_{0z}$
, (b)
$\unicode[STIX]{x1D6FF}B_{0}/\sqrt{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}=0.5c_{s}\approx 3.3B_{0z}$
, (b)
![]() $\unicode[STIX]{x1D6FF}B_{0}/\sqrt{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}=c_{s}\approx 6.7B_{0z}$
, (c)
$\unicode[STIX]{x1D6FF}B_{0}/\sqrt{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}=c_{s}\approx 6.7B_{0z}$
, (c)
![]() $\unicode[STIX]{x1D6FF}B_{0}/\sqrt{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}=2c_{s}\approx 13.3B_{0z}$
. Note that
$\unicode[STIX]{x1D6FF}B_{0}/\sqrt{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}=2c_{s}\approx 13.3B_{0z}$
. Note that
![]() $\unicode[STIX]{x1D6E5}=0.1$
would correspond to a plasma fixed at the mirror limit in a constant background field
$\unicode[STIX]{x1D6E5}=0.1$
would correspond to a plasma fixed at the mirror limit in a constant background field
![]() $B_{0}\approx \sqrt{8\unicode[STIX]{x03C0}\unicode[STIX]{x0394}p_{0}}\approx 0.45c_{s}\sqrt{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}$
(but note that the channel-mode field varies sinusoidally). In each figure the yellow stars illustrate the growth rate in KMHD without heat fluxes (i.e. CGL,
$B_{0}\approx \sqrt{8\unicode[STIX]{x03C0}\unicode[STIX]{x0394}p_{0}}\approx 0.45c_{s}\sqrt{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}$
(but note that the channel-mode field varies sinusoidally). In each figure the yellow stars illustrate the growth rate in KMHD without heat fluxes (i.e. CGL,
![]() $q_{\bot }=q_{\Vert }=0$
), while purple crosses illustrate KMHD growth rates including the simple model (2.12) for the heat fluxes. For comparison, the dashed blue line shows the incompressible MHD result and the dash-dotted red line shows the isothermal compressible MHD result (each at
$q_{\bot }=q_{\Vert }=0$
), while purple crosses illustrate KMHD growth rates including the simple model (2.12) for the heat fluxes. For comparison, the dashed blue line shows the incompressible MHD result and the dash-dotted red line shows the isothermal compressible MHD result (each at
![]() $\unicode[STIX]{x1D6E5}=0$
). The dotted black line is the MRI channel-mode growth rate
$\unicode[STIX]{x1D6E5}=0$
). The dotted black line is the MRI channel-mode growth rate
![]() $\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D6FA}=3/4$
. Evidently, the variation of
$\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D6FA}=3/4$
. Evidently, the variation of
![]() $\unicode[STIX]{x1D6FE}$
with
$\unicode[STIX]{x1D6FE}$
with
![]() $\unicode[STIX]{x1D6E5}$
is modest, and is probably too small to be of much consequence to MRI saturation.
$\unicode[STIX]{x1D6E5}$
is modest, and is probably too small to be of much consequence to MRI saturation.
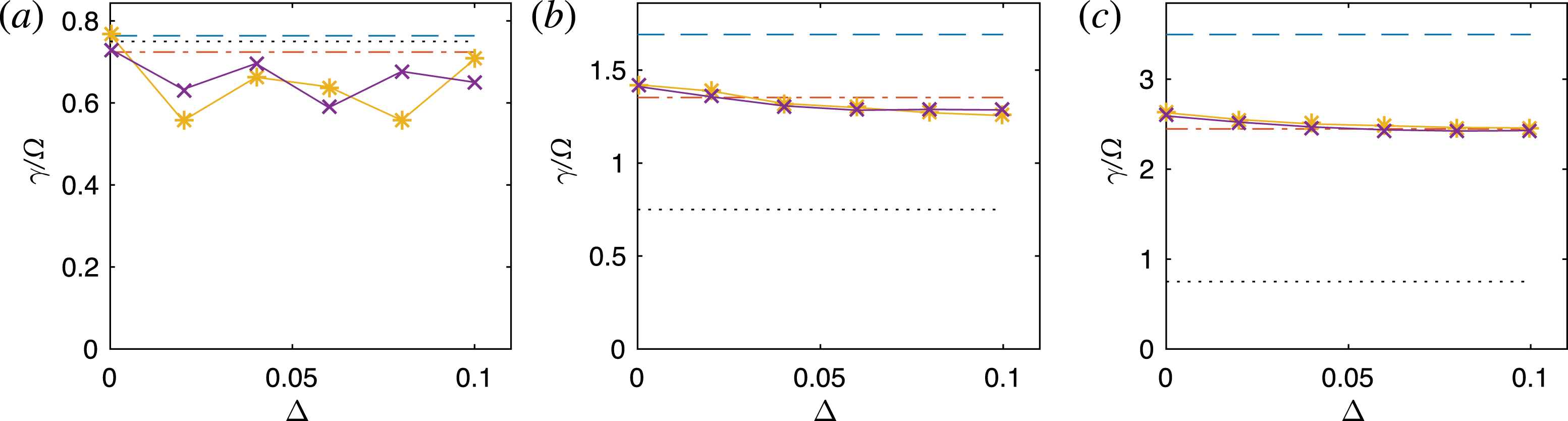
Figure 5. As in figure 4 but with a background field
![]() $\unicode[STIX]{x1D6FD}_{0}\approx 800$
(
$\unicode[STIX]{x1D6FD}_{0}\approx 800$
(
![]() $B_{0z}/\sqrt{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}=0.05c_{s}$
). Although a growing MRI mode would have a shorter wavelength at this
$B_{0z}/\sqrt{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}=0.05c_{s}$
). Although a growing MRI mode would have a shorter wavelength at this
![]() $B_{0z}$
, which will make the parasitic modes more unstable at a given amplitude due to the larger gradients, we choose to keep the same
$B_{0z}$
, which will make the parasitic modes more unstable at a given amplitude due to the larger gradients, we choose to keep the same
![]() $k=2\unicode[STIX]{x03C0}/L_{z}$
as figure 4 to provide a direct comparison (recall also from § 3 that the mode wavelength can increase during evolution).
$k=2\unicode[STIX]{x03C0}/L_{z}$
as figure 4 to provide a direct comparison (recall also from § 3 that the mode wavelength can increase during evolution).
Figures 4 and 5 illustrate representative examples of
![]() $\unicode[STIX]{x1D6FE}$
as a function of
$\unicode[STIX]{x1D6FE}$
as a function of
![]() $\unicode[STIX]{x1D6E5}=(\unicode[STIX]{x1D6FF}p_{\bot 0}-\unicode[STIX]{x1D6FF}p_{\Vert 0})/p_{0}$
and
$\unicode[STIX]{x1D6E5}=(\unicode[STIX]{x1D6FF}p_{\bot 0}-\unicode[STIX]{x1D6FF}p_{\Vert 0})/p_{0}$
and
![]() $\unicode[STIX]{x1D6FF}B_{0}$
. In each case the chosen mode energy is of order the thermal energy
$\unicode[STIX]{x1D6FF}B_{0}$
. In each case the chosen mode energy is of order the thermal energy
![]() $\unicode[STIX]{x1D6FF}B_{0}/\sqrt{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}\sim c_{s}$
and is larger than the background
$\unicode[STIX]{x1D6FF}B_{0}/\sqrt{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}\sim c_{s}$
and is larger than the background
![]() $B_{0z}$
field. Because of this large
$B_{0z}$
field. Because of this large
![]() $\unicode[STIX]{x1D6FF}B_{0}$
, the parasitic growth rates are mostly larger than the MRI-mode growth rate (dotted line), as required for a parasite to cause the channel mode to break up into turbulence. The maximum of
$\unicode[STIX]{x1D6FF}B_{0}$
, the parasitic growth rates are mostly larger than the MRI-mode growth rate (dotted line), as required for a parasite to cause the channel mode to break up into turbulence. The maximum of
![]() $\unicode[STIX]{x1D6E5}$
plotted (
$\unicode[STIX]{x1D6E5}$
plotted (
![]() $\unicode[STIX]{x1D6E5}=0.1$
) corresponds to a plasma that is everywhere at the mirror limit in a constant field of
$\unicode[STIX]{x1D6E5}=0.1$
) corresponds to a plasma that is everywhere at the mirror limit in a constant field of
![]() $B_{0}\approx \sqrt{8\unicode[STIX]{x03C0}\unicode[STIX]{x0394}p_{0}}\approx 0.45c_{s}\sqrt{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}$
, which is larger than the background
$B_{0}\approx \sqrt{8\unicode[STIX]{x03C0}\unicode[STIX]{x0394}p_{0}}\approx 0.45c_{s}\sqrt{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}$
, which is larger than the background
![]() $B_{0z}$
in each case (but smaller than the maximum
$B_{0z}$
in each case (but smaller than the maximum
![]() $\unicode[STIX]{x1D6FF}B_{0}$
studied). The first feature that is evident in figures 4 and 5 is the suppression in parasitic-mode growth rates in the kinetic models (solid lines) and compressible fluids (red dash-dotted line), in comparison to incompressible fluids (blue dashed line). This property was also noted for compressible MHD in Latter et al. (Reference Latter, Lesaffre and Balbus2009).Footnote
9
Aside from this, we see that the differences between the kinetic models (both with and without heat fluxes) and MHD are relatively modest.Footnote
10
While there is there is a slight tendency for
$\unicode[STIX]{x1D6FF}B_{0}$
studied). The first feature that is evident in figures 4 and 5 is the suppression in parasitic-mode growth rates in the kinetic models (solid lines) and compressible fluids (red dash-dotted line), in comparison to incompressible fluids (blue dashed line). This property was also noted for compressible MHD in Latter et al. (Reference Latter, Lesaffre and Balbus2009).Footnote
9
Aside from this, we see that the differences between the kinetic models (both with and without heat fluxes) and MHD are relatively modest.Footnote
10
While there is there is a slight tendency for
![]() $\unicode[STIX]{x1D6FE}$
to decrease with
$\unicode[STIX]{x1D6FE}$
to decrease with
![]() $\unicode[STIX]{x0394}p$
at large mode amplitudes, changes in
$\unicode[STIX]{x0394}p$
at large mode amplitudes, changes in
![]() $\unicode[STIX]{x1D6FE}$
of this magnitude are unlikely to make any notable differences in a nonlinear simulation. Furthermore, there does not appear to be any significant change in behaviour at even higher
$\unicode[STIX]{x1D6FE}$
of this magnitude are unlikely to make any notable differences in a nonlinear simulation. Furthermore, there does not appear to be any significant change in behaviour at even higher
![]() $\unicode[STIX]{x1D6FF}B_{0}$
(not shown), which leads us to conclude that parasitic modes are broadly unaffected by the kinetic effects contained within the CGL and LF models.
$\unicode[STIX]{x1D6FF}B_{0}$
(not shown), which leads us to conclude that parasitic modes are broadly unaffected by the kinetic effects contained within the CGL and LF models.
Obviously, the results shown in figures 4 and 5 cover only a small portion of parameter space in a rather idealized setting. In addition to the results shown, we have calculated growth rates across a much wider parameter space in
![]() $B_{0z}$
,
$B_{0z}$
,
![]() $p_{0}$
,
$p_{0}$
,
![]() $\unicode[STIX]{x1D6FF}B_{0}$
,
$\unicode[STIX]{x1D6FF}B_{0}$
,
![]() $\unicode[STIX]{x1D6E5}$
,
$\unicode[STIX]{x1D6E5}$
,
![]() $k$
(the channel mode wavelength), small-scale dissipation coefficients (hyper-viscosity, hyper-resistivity and their ratio) and box dimensions. In addition, we have varied the ratio of
$k$
(the channel mode wavelength), small-scale dissipation coefficients (hyper-viscosity, hyper-resistivity and their ratio) and box dimensions. In addition, we have varied the ratio of
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{u}$
and
$\unicode[STIX]{x1D6FF}\boldsymbol{u}$
and
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{B}$
away from that of the fastest-growing channel mode (i.e. differently from (3.1)), as might be caused, for example, by the effects of the self-generated pressure anisotropy on the mode. Finally, we have also considered parasitic-mode evolution on more angular compressible profiles, similar to those shown in figure 2(d) (Latter et al.
Reference Latter, Lesaffre and Balbus2009). In all cases, we have failed to find any significant difference between standard compressible MHD and the CGL or LF models, and so we refrain from presenting these results in any detail here. Of course, these studies have all assumed a spatially constant
$\unicode[STIX]{x1D6FF}\boldsymbol{B}$
away from that of the fastest-growing channel mode (i.e. differently from (3.1)), as might be caused, for example, by the effects of the self-generated pressure anisotropy on the mode. Finally, we have also considered parasitic-mode evolution on more angular compressible profiles, similar to those shown in figure 2(d) (Latter et al.
Reference Latter, Lesaffre and Balbus2009). In all cases, we have failed to find any significant difference between standard compressible MHD and the CGL or LF models, and so we refrain from presenting these results in any detail here. Of course, these studies have all assumed a spatially constant
![]() $\unicode[STIX]{x1D6E5}$
and
$\unicode[STIX]{x1D6E5}$
and
![]() $\unicode[STIX]{x1D70C}_{0}$
profile, which will certainly change results quantitatively in some regimes. It is also possible that there are modes in other regimes (e.g. much longer or shorter wavelength than the KMRI mode), that have not been captured by these studies. Nevertheless, we feel that the general conclusion that the parasitic modes are mostly insensitive to background pressure anisotropy should be robust, given the wide range of parameter space for which this conclusion appears to hold.
$\unicode[STIX]{x1D70C}_{0}$
profile, which will certainly change results quantitatively in some regimes. It is also possible that there are modes in other regimes (e.g. much longer or shorter wavelength than the KMRI mode), that have not been captured by these studies. Nevertheless, we feel that the general conclusion that the parasitic modes are mostly insensitive to background pressure anisotropy should be robust, given the wide range of parameter space for which this conclusion appears to hold.
4.2 Nonlinear simulation
Our second method for probing parasitic-mode behaviour is to simply observe the evolution of a nonlinear KMRI channel mode in three dimensions. The maximum amplitude that such a mode reaches before breaking up into turbulence should give a simple indication of the effectiveness of the parasitic modes. We use the modified version of the Zeus code described in Reference Sharma, Hammett, Quataert and StoneS06, which solves (2.1)–(2.5) with the LF closure (2.6)–(2.7) and pressure-anisotropy limiters.
This method is complementary to that described in the previous section: although it cannot provide detailed information on individual modes or variation with parameters, it is free from some of the caveats of the linear parasitic-mode study (for example, the assumption of spatially homogeneous background density profiles). It also allows us to consider the mixed-azimuthal–vertical field KMRI in a moderately realistic settling (as mentioned above, the stronger effects of 1-D nonlinearities in this case suggest that an idealized parasitic-mode study is not very worthwhile for the azimuthal-field KMRI). Most importantly, 3-D simulations directly address the issue we most care about: is the nonlinear saturation significantly different between the kinetic and MHD models? In Reference Sharma, Hammett, Quataert and StoneS06 the authors noted that there was a significant difference, with MRI modes in kinetic models growing to significantly larger amplitudes before being disrupted, even though the turbulence itself maintained a similar level of angular-momentum transport. While this may appear to be at odds with our findings from the previous section, here we argue that this difference is primarily a consequence of the 1-D effects described in § 3. Specifically, the positive pressure anisotropy can increase the wavelength of the mode well before it reaches saturation amplitudes. This effect was caused by the choice of
![]() $\unicode[STIX]{x1D6E5}\approx 7/\unicode[STIX]{x1D6FD}$
for the mirror instability limit in Reference Sharma, Hammett, Quataert and StoneS06, which allows the anisotropies to have a strong dynamical effect before the mirror limit is enforced. For a given mode amplitude, these longer-wavelength modes are attacked more slowly by the parasites, due to the smaller gradients of
$\unicode[STIX]{x1D6E5}\approx 7/\unicode[STIX]{x1D6FD}$
for the mirror instability limit in Reference Sharma, Hammett, Quataert and StoneS06, which allows the anisotropies to have a strong dynamical effect before the mirror limit is enforced. For a given mode amplitude, these longer-wavelength modes are attacked more slowly by the parasites, due to the smaller gradients of
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{u}$
and
$\unicode[STIX]{x1D6FF}\boldsymbol{u}$
and
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{B}$
(Goodman & Xu Reference Goodman and Xu1994), thus leading to a larger transient amplitude before the transition into turbulence.
$\unicode[STIX]{x1D6FF}\boldsymbol{B}$
(Goodman & Xu Reference Goodman and Xu1994), thus leading to a larger transient amplitude before the transition into turbulence.
Our studies have deliberately used a set-up that is similar to Reference Sharma, Hammett, Quataert and StoneS06. We initialize with random noise in all variables and a background magnetic field with
![]() $\unicode[STIX]{x1D6FD}_{0}=400$
in a box of dimension
$\unicode[STIX]{x1D6FD}_{0}=400$
in a box of dimension
![]() $(L_{x},L_{y},L_{z})=(1,2\unicode[STIX]{x03C0},1)$
. We take
$(L_{x},L_{y},L_{z})=(1,2\unicode[STIX]{x03C0},1)$
. We take
![]() $k_{L}\approx 14$
, which corresponds to capturing Landau damping correctly (
$k_{L}\approx 14$
, which corresponds to capturing Landau damping correctly (
![]() $k_{\Vert }\approx k_{L}$
) for low-amplitude modes with a wavelength of approximately half of the size of the box, and limit the positive pressure anisotropy at
$k_{\Vert }\approx k_{L}$
) for low-amplitude modes with a wavelength of approximately half of the size of the box, and limit the positive pressure anisotropy at
![]() $p_{\bot }/p_{\Vert }-1<\unicode[STIX]{x1D709}_{\text{Mir}}/\unicode[STIX]{x1D6FD}_{\bot }$
(this is
$p_{\bot }/p_{\Vert }-1<\unicode[STIX]{x1D709}_{\text{Mir}}/\unicode[STIX]{x1D6FD}_{\bot }$
(this is
![]() $\unicode[STIX]{x1D6E5}<\unicode[STIX]{x1D709}_{\text{Mir}}/\unicode[STIX]{x1D6FD}$
for
$\unicode[STIX]{x1D6E5}<\unicode[STIX]{x1D709}_{\text{Mir}}/\unicode[STIX]{x1D6FD}$
for
![]() $\unicode[STIX]{x0394}p\ll p_{0}$
). With either a purely vertical background field, or a mixed-azimuthal–vertical background field (
$\unicode[STIX]{x0394}p\ll p_{0}$
). With either a purely vertical background field, or a mixed-azimuthal–vertical background field (
![]() $B_{0y}=B_{0z}$
), we compare the mode saturation between MHD, the LF model with
$B_{0y}=B_{0z}$
), we compare the mode saturation between MHD, the LF model with
![]() $\unicode[STIX]{x1D709}_{\text{Mir}}=7$
, and the LF model with
$\unicode[STIX]{x1D709}_{\text{Mir}}=7$
, and the LF model with
![]() $\unicode[STIX]{x1D709}_{\text{Mir}}=1$
. The vertical-field LF model runs are identical to runs Zl4 and Zl5 of Reference Sharma, Hammett, Quataert and StoneS06.
$\unicode[STIX]{x1D709}_{\text{Mir}}=1$
. The vertical-field LF model runs are identical to runs Zl4 and Zl5 of Reference Sharma, Hammett, Quataert and StoneS06.
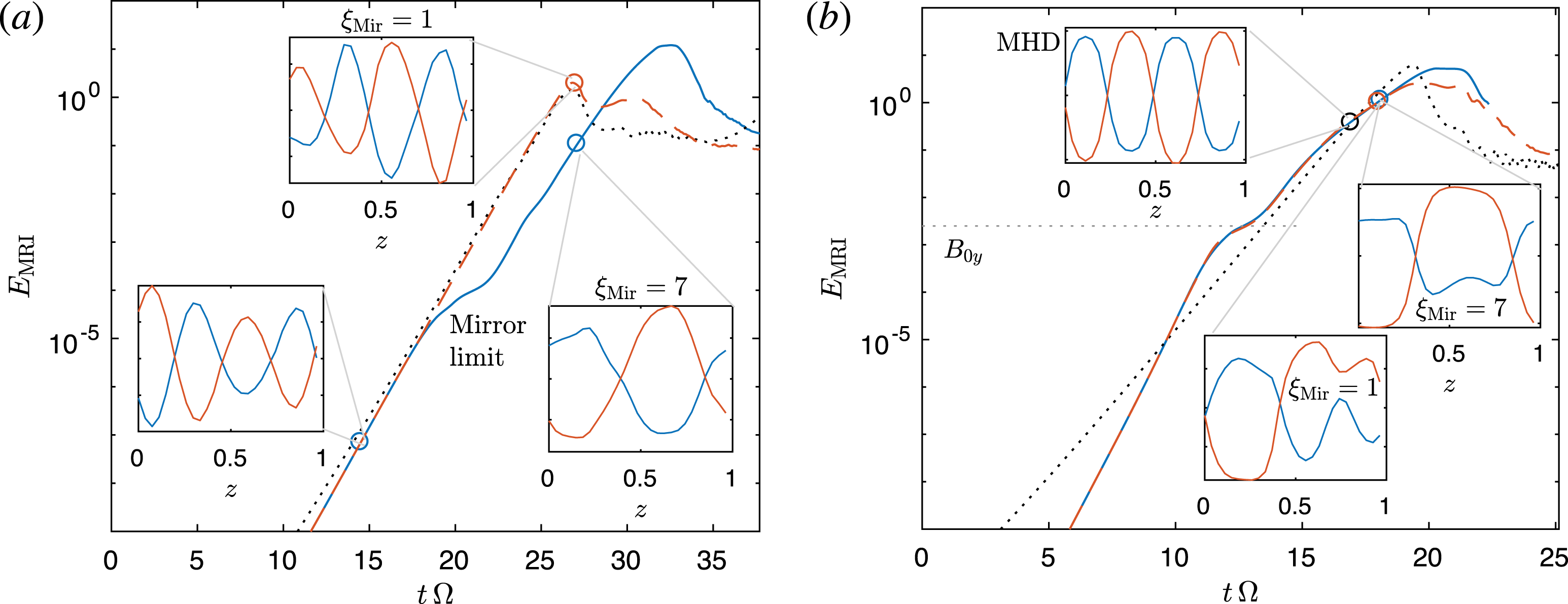
Figure 6. Energy of the MRI perturbation,
![]() $E_{\text{MRI}}=\int \text{d}z\,(\unicode[STIX]{x1D70C}\,\unicode[STIX]{x1D6FF}u^{2}/2+\unicode[STIX]{x1D6FF}B^{2}/8\unicode[STIX]{x03C0})$
, as a function of time for a set of 3-D Zeus simulations at
$E_{\text{MRI}}=\int \text{d}z\,(\unicode[STIX]{x1D70C}\,\unicode[STIX]{x1D6FF}u^{2}/2+\unicode[STIX]{x1D6FF}B^{2}/8\unicode[STIX]{x03C0})$
, as a function of time for a set of 3-D Zeus simulations at
![]() $\unicode[STIX]{x1D6FD}_{0}=400$
. We compare the evolution of the LF model (2.1)–(2.7) with mirror limiter
$\unicode[STIX]{x1D6FD}_{0}=400$
. We compare the evolution of the LF model (2.1)–(2.7) with mirror limiter
![]() $\unicode[STIX]{x1D6E5}=7/\unicode[STIX]{x1D6FD}$
as used in Reference Sharma, Hammett, Quataert and StoneS06 (blue solid lines), the LF model with mirror limiter
$\unicode[STIX]{x1D6E5}=7/\unicode[STIX]{x1D6FD}$
as used in Reference Sharma, Hammett, Quataert and StoneS06 (blue solid lines), the LF model with mirror limiter
![]() $\unicode[STIX]{x1D6E5}=1/\unicode[STIX]{x1D6FD}$
(red dashed lines) and standard MHD (black dotted lines). The insets show the vertical mode structure (
$\unicode[STIX]{x1D6E5}=1/\unicode[STIX]{x1D6FD}$
(red dashed lines) and standard MHD (black dotted lines). The insets show the vertical mode structure (
![]() $\unicode[STIX]{x1D6FF}B_{x}$
, blue;
$\unicode[STIX]{x1D6FF}B_{x}$
, blue;
![]() $\unicode[STIX]{x1D6FF}B_{y}$
, red) at the times indicated by the circles. Panel (a) shows the case with a purely vertical background magnetic field (
$\unicode[STIX]{x1D6FF}B_{y}$
, red) at the times indicated by the circles. Panel (a) shows the case with a purely vertical background magnetic field (
![]() $B_{0y}=0$
). This illustrates how an artificially high mirror limit (
$B_{0y}=0$
). This illustrates how an artificially high mirror limit (
![]() $\unicode[STIX]{x1D6E5}=7/\unicode[STIX]{x1D6FD}$
; blue solid line) causes the mode to move to longer wavelengths after it reaches the mirror limit at
$\unicode[STIX]{x1D6E5}=7/\unicode[STIX]{x1D6FD}$
; blue solid line) causes the mode to move to longer wavelengths after it reaches the mirror limit at
![]() $t\approx 17$
, which subsequently causes the mode to reach a very large amplitude before saturation. Panel (b) shows simulations with an azimuthal background magnetic field (
$t\approx 17$
, which subsequently causes the mode to reach a very large amplitude before saturation. Panel (b) shows simulations with an azimuthal background magnetic field (
![]() $B_{0y}=B_{0z}$
; the dotted line shows the energy of
$B_{0y}=B_{0z}$
; the dotted line shows the energy of
![]() $B_{0y}$
); in this case, all three modes saturate into turbulence at similar amplitudes. Given the relatively disordered mode structure in the kinetic runs (the insets compare the late-time structures of all three cases, as labelled), this behaviour is consistent with the idea that there are not major differences between the parasitic modes’ properties in the kinetic (LF) model and MHD (see text for further discussion). Note that the time scale of the MHD case in panel (b) has been shifted to the left, so that all three modes reach saturation amplitudes at a similar time (the linear growth of the KMRI mode is faster, see figure 1).
$B_{0y}$
); in this case, all three modes saturate into turbulence at similar amplitudes. Given the relatively disordered mode structure in the kinetic runs (the insets compare the late-time structures of all three cases, as labelled), this behaviour is consistent with the idea that there are not major differences between the parasitic modes’ properties in the kinetic (LF) model and MHD (see text for further discussion). Note that the time scale of the MHD case in panel (b) has been shifted to the left, so that all three modes reach saturation amplitudes at a similar time (the linear growth of the KMRI mode is faster, see figure 1).
Our findings are illustrated in figure 6, which plots the modes’ energy evolution in both LF cases and standard MHD, with a purely vertical field (left-hand panel a) and with a mixed-azimuthal–vertical field (right-hand panel b). The key result of this figure is the larger (
![]() ${\sim}$
factor
${\sim}$
factor
![]() $10$
) overshoot of the vertical-field KMRI mode (panel a) with
$10$
) overshoot of the vertical-field KMRI mode (panel a) with
![]() $\unicode[STIX]{x1D709}_{\text{Mir}}=7$
(compared to MHD), which disappears at
$\unicode[STIX]{x1D709}_{\text{Mir}}=7$
(compared to MHD), which disappears at
![]() $\unicode[STIX]{x1D709}_{\text{Mir}}=1$
(i.e. there is effectively no difference between MHD and the LF model with the
$\unicode[STIX]{x1D709}_{\text{Mir}}=1$
(i.e. there is effectively no difference between MHD and the LF model with the
![]() $\unicode[STIX]{x1D709}_{\text{Mir}}=1$
mirror limiter). As mentioned above, this leads us to attribute the differences between MHD and the LF model saturation to the difference in the large-amplitude wavelength of the MRI modes. Specifically, the strength of the vertical magnetic field for
$\unicode[STIX]{x1D709}_{\text{Mir}}=1$
mirror limiter). As mentioned above, this leads us to attribute the differences between MHD and the LF model saturation to the difference in the large-amplitude wavelength of the MRI modes. Specifically, the strength of the vertical magnetic field for
![]() $\unicode[STIX]{x1D6FD}_{0}=400$
is such that modes with
$\unicode[STIX]{x1D6FD}_{0}=400$
is such that modes with
![]() $k_{z}=4\unicode[STIX]{x03C0}/L_{z}$
dominate during the linear phase, but, with the artificially high mirror boundary
$k_{z}=4\unicode[STIX]{x03C0}/L_{z}$
dominate during the linear phase, but, with the artificially high mirror boundary
![]() $\unicode[STIX]{x1D709}_{\text{Mir}}=7$
,
$\unicode[STIX]{x1D709}_{\text{Mir}}=7$
,
![]() $\unicode[STIX]{x1D6E5}$
becomes large enough to cause the KMRI mode to increase in scale to the largest in the box by later times (see insets). This does not occur with the standard mirror limit
$\unicode[STIX]{x1D6E5}$
becomes large enough to cause the KMRI mode to increase in scale to the largest in the box by later times (see insets). This does not occur with the standard mirror limit
![]() $\unicode[STIX]{x1D709}_{\text{Mir}}=1$
. While not unexpected, these results do show that there are not inherent differences in the parasitic modes’ properties between the kinetic (LF) model and MHD for the vertical-field MRI. Examination of mode evolution at a variety of other values for
$\unicode[STIX]{x1D709}_{\text{Mir}}=1$
. While not unexpected, these results do show that there are not inherent differences in the parasitic modes’ properties between the kinetic (LF) model and MHD for the vertical-field MRI. Examination of mode evolution at a variety of other values for
![]() $\unicode[STIX]{x1D6FD}_{0}$
and
$\unicode[STIX]{x1D6FD}_{0}$
and
![]() $\unicode[STIX]{x1D709}_{\text{Mir}}$
(not shown) has produced results that are generally consistent with this idea.
$\unicode[STIX]{x1D709}_{\text{Mir}}$
(not shown) has produced results that are generally consistent with this idea.
In figure 6(b), showing a mixed-azimuthal–vertical background field configuration, we see that the saturation amplitudes of all three cases (the MHD model, and the
![]() $\unicode[STIX]{x1D709}_{\text{Mir}}=1$
and
$\unicode[STIX]{x1D709}_{\text{Mir}}=1$
and
![]() $\unicode[STIX]{x1D709}_{\text{Mir}}=7$
LF models) are similar. This seems to be because even at large amplitudes, the KMRI modes are relatively disordered and each have both
$\unicode[STIX]{x1D709}_{\text{Mir}}=7$
LF models) are similar. This seems to be because even at large amplitudes, the KMRI modes are relatively disordered and each have both
![]() $k=2\unicode[STIX]{x03C0}/L_{z}$
and
$k=2\unicode[STIX]{x03C0}/L_{z}$
and
![]() $k=4\unicode[STIX]{x03C0}/L_{z}$
components, while the MHD mode is nearly a pure
$k=4\unicode[STIX]{x03C0}/L_{z}$
components, while the MHD mode is nearly a pure
![]() $k=4\unicode[STIX]{x03C0}/L_{z}$
mode. This more disordered KMRI state is expected based on the 1-D analysis of § 3.3: the mode is strongly disrupted as
$k=4\unicode[STIX]{x03C0}/L_{z}$
mode. This more disordered KMRI state is expected based on the 1-D analysis of § 3.3: the mode is strongly disrupted as
![]() $\unicode[STIX]{x1D6FF}B_{y}$
surpasses
$\unicode[STIX]{x1D6FF}B_{y}$
surpasses
![]() $B_{0y}$
, and has not had time to ‘pick out’ the fastest-growing mode (see also figure 3
b). Thus although the MHD mode might be more easily attacked by the parasitic modes (given its smaller scale), the more disordered KMRI modes are further from being nonlinear solutions, and thus more easily evolve into turbulence. The net result is that they all saturate at approximately the same amplitude. As further evidence for this scenario, we see that the
$B_{0y}$
, and has not had time to ‘pick out’ the fastest-growing mode (see also figure 3
b). Thus although the MHD mode might be more easily attacked by the parasitic modes (given its smaller scale), the more disordered KMRI modes are further from being nonlinear solutions, and thus more easily evolve into turbulence. The net result is that they all saturate at approximately the same amplitude. As further evidence for this scenario, we see that the
![]() $k=2\unicode[STIX]{x03C0}/L_{z}$
component of the
$k=2\unicode[STIX]{x03C0}/L_{z}$
component of the
![]() $\unicode[STIX]{x1D709}_{\text{Mir}}=7$
mode is larger than that of the
$\unicode[STIX]{x1D709}_{\text{Mir}}=7$
mode is larger than that of the
![]() $\unicode[STIX]{x1D709}_{\text{Mir}}=1$
mode (as expected because
$\unicode[STIX]{x1D709}_{\text{Mir}}=1$
mode (as expected because
![]() $\unicode[STIX]{x0394}p$
is larger, increasing the effective magnetic tension), explaining its slightly higher saturation amplitude. Thus, these mixed-azimuthal–vertical field KMRI results also suggest that there is little difference between the parasitic-mode properties in the kinetic (LF) model and MHD. Again, we have examined mode evolution at various other values for
$\unicode[STIX]{x0394}p$
is larger, increasing the effective magnetic tension), explaining its slightly higher saturation amplitude. Thus, these mixed-azimuthal–vertical field KMRI results also suggest that there is little difference between the parasitic-mode properties in the kinetic (LF) model and MHD. Again, we have examined mode evolution at various other values for
![]() $\unicode[STIX]{x1D6FD}_{0}$
and
$\unicode[STIX]{x1D6FD}_{0}$
and
![]() $\unicode[STIX]{x1D709}_{\text{Mir}}$
(not shown) and seen similar results; however, to truly study this case in detail would require much higher resolution simulations (so as to allow higher
$\unicode[STIX]{x1D709}_{\text{Mir}}$
(not shown) and seen similar results; however, to truly study this case in detail would require much higher resolution simulations (so as to allow higher
![]() $\unicode[STIX]{x1D6FD}_{0}$
; see figure 3), which are beyond the scope of this work.
$\unicode[STIX]{x1D6FD}_{0}$
; see figure 3), which are beyond the scope of this work.
Overall, we see that all of our calculations – both of linear parasitic-mode growth rates in idealized settings and 3-D studies using the full nonlinear LF model – are consistent with the idea that parasitic modes are not strongly affected by the kinetic effects contained within the fluid models considered in this work. This seems to be the case for both the vertical-field KMRI and the mixed-azimuthal–vertical field KMRI (although we did not study the parasitic modes directly for the mixed-field case). An obvious caveat of this conclusion is that we have considered only the LF model in this work, and future studies with fully kinetic methods (in particular, those that can correctly capture plasma microinstability saturation) are needed to shed light on whether our conclusions also hold for truly collisionless plasmas.
5 Kinetic effects not included in our models
Our approach throughout this paper has been to consider only the simplest kinetic effects, in particular those arising from a self-generated gyrotropic
![]() $\unicode[STIX]{x0394}p$
. Further, the Landau-fluid models used for much of the kinetic modelling do not correctly capture the all-important firehose and mirror microinstabilities, and we have resorted to applying phenomenological hard-wall limits as commonly used in previous works (Reference Sharma, Hammett, Quataert and StoneS06; Sharma et al.
Reference Sharma, Quataert, Hammett and Stone2007, Santos-Lima et al.
Reference Santos-Lima, de Gouveia Dal Pino, Kowal, Falceta-Gonçalves, Lazarian and Nakwacki2014). In this section we briefly outline some physical effects that are not included in our model, most of which must be examined, in one way or another, through fully kinetic simulations (e.g. Kunz et al.
Reference Kunz, Stone and Quataert2016).
$\unicode[STIX]{x0394}p$
. Further, the Landau-fluid models used for much of the kinetic modelling do not correctly capture the all-important firehose and mirror microinstabilities, and we have resorted to applying phenomenological hard-wall limits as commonly used in previous works (Reference Sharma, Hammett, Quataert and StoneS06; Sharma et al.
Reference Sharma, Quataert, Hammett and Stone2007, Santos-Lima et al.
Reference Santos-Lima, de Gouveia Dal Pino, Kowal, Falceta-Gonçalves, Lazarian and Nakwacki2014). In this section we briefly outline some physical effects that are not included in our model, most of which must be examined, in one way or another, through fully kinetic simulations (e.g. Kunz et al.
Reference Kunz, Stone and Quataert2016).
Mirror and firehose evolution. Recent kinetic simulations and analytical calculations (Kunz et al.
Reference Kunz, Schekochihin and Stone2014a
; Hellinger et al.
Reference Hellinger, Matteini, Landi, Verdini, Franci and Trávníček2015; Rincon et al.
Reference Rincon, Schekochihin and Cowley2015; Melville et al.
Reference Melville, Schekochihin and Kunz2016) paint an interesting picture of how the firehose and mirror instabilities saturate, with each going through a regime where fluctuations grow secularly with little particle scattering, followed by a saturated regime in which the microinstabilities strongly scatter particles due to sharp small-scale irregularities in the magnetic field. The mirror instability is particularly interesting, both because it is more important than the firehose for MRI dynamics (since
![]() $\text{d}B/\text{d}t>0$
quite generally), and because it grows secularly over macroscopic time scales (i.e. for
$\text{d}B/\text{d}t>0$
quite generally), and because it grows secularly over macroscopic time scales (i.e. for
![]() $t\sim |\unicode[STIX]{x1D735}\boldsymbol{u}|^{-1}$
) before saturating and scattering particles (Kunz et al.
Reference Kunz, Schekochihin and Stone2014a
; Rincon et al.
Reference Rincon, Schekochihin and Cowley2015; Riquelme et al.
Reference Riquelme, Quataert and Verscharen2015; Melville et al.
Reference Melville, Schekochihin and Kunz2016). This may add another time scale and nonlinear feature into the 1-D MRI evolution described in § 3, whereby the effective collisionality is strongly enhanced some time
$t\sim |\unicode[STIX]{x1D735}\boldsymbol{u}|^{-1}$
) before saturating and scattering particles (Kunz et al.
Reference Kunz, Schekochihin and Stone2014a
; Rincon et al.
Reference Rincon, Schekochihin and Cowley2015; Riquelme et al.
Reference Riquelme, Quataert and Verscharen2015; Melville et al.
Reference Melville, Schekochihin and Kunz2016). This may add another time scale and nonlinear feature into the 1-D MRI evolution described in § 3, whereby the effective collisionality is strongly enhanced some time
![]() $t\sim \unicode[STIX]{x1D6FA}^{-1}$
after
$t\sim \unicode[STIX]{x1D6FA}^{-1}$
after
![]() $\unicode[STIX]{x0394}p$
initially reaches the mirror limit. It is unclear if there will be a significant change in macroscopic behaviour with the onset of particle scattering, and fully kinetic MRI simulations with large scale separations
$\unicode[STIX]{x0394}p$
initially reaches the mirror limit. It is unclear if there will be a significant change in macroscopic behaviour with the onset of particle scattering, and fully kinetic MRI simulations with large scale separations
![]() $\unicode[STIX]{x1D6FA}/\unicode[STIX]{x1D6FA}_{i}\gg 1$
are needed to address this issue (see § 6 for further discussion).
$\unicode[STIX]{x1D6FA}/\unicode[STIX]{x1D6FA}_{i}\gg 1$
are needed to address this issue (see § 6 for further discussion).
Other kinetic instabilities. There are a variety of other pressure-anisotropy-induced kinetic instabilities that we have ignored throughout this work. For the ion dynamics, the most important of these is likely the ion-cyclotron instability (see, e.g. Gary, McKean & Winske Reference Gary, McKean and Winske1993). While general theoretical analysis (Gary et al.
Reference Gary, Wang, Winske and Fuselier1997; Reference Sharma, Hammett, Quataert and StoneS06) and solar-wind observations/theory (Kasper, Lazarus & Gary Reference Kasper, Lazarus and Gary2002; Bale et al.
Reference Bale, Kasper, Howes, Quataert, Salem and Sundkvist2009; Verscharen et al.
Reference Verscharen, Chandran, Klein and Quataert2016) suggest that the ion-cyclotron instability is less important than the mirror instability when
![]() $T_{e}\sim T_{i}$
and
$T_{e}\sim T_{i}$
and
![]() $\unicode[STIX]{x1D6FD}_{0}\gtrsim 1$
, it may become more important at lower
$\unicode[STIX]{x1D6FD}_{0}\gtrsim 1$
, it may become more important at lower
![]() $T_{e}/T_{i}$
(as expected in low-luminosity accretion flows). In particular, the works of Sironi (Reference Sironi2015) and Sironi & Narayan (Reference Sironi and Narayan2015) suggest that there is a transition around
$T_{e}/T_{i}$
(as expected in low-luminosity accretion flows). In particular, the works of Sironi (Reference Sironi2015) and Sironi & Narayan (Reference Sironi and Narayan2015) suggest that there is a transition around
![]() $T_{e}/T_{i}\lesssim 0.2$
(or somewhat lower when
$T_{e}/T_{i}\lesssim 0.2$
(or somewhat lower when
![]() $\unicode[STIX]{x1D6FD}_{i}\gtrsim 30$
) below which the ion-cyclotron instability dominates over the mirror instability in regulating pressure anisotropy (this behaviour is at least partially accounted for by the linear effects of electron pressure anisotropy; see Pokhotelov et al.
Reference Pokhotelov, Balikhin, Alleyne and Onishchenko2000, Remya et al.
Reference Remya, Reddy, Tsurutani, Lakhina and Echer2013). At least for lower
$\unicode[STIX]{x1D6FD}_{i}\gtrsim 30$
) below which the ion-cyclotron instability dominates over the mirror instability in regulating pressure anisotropy (this behaviour is at least partially accounted for by the linear effects of electron pressure anisotropy; see Pokhotelov et al.
Reference Pokhotelov, Balikhin, Alleyne and Onishchenko2000, Remya et al.
Reference Remya, Reddy, Tsurutani, Lakhina and Echer2013). At least for lower
![]() $\unicode[STIX]{x1D6FD}_{i}$
plasmas, this will modify the threshold at which the pressure anisotropy is nonlinearly regulated (see §2.3 of Reference Sharma, Hammett, Quataert and StoneS06) and change the microphysical mechanism through which this regulation occurs (Sironi & Narayan Reference Sironi and Narayan2015).
$\unicode[STIX]{x1D6FD}_{i}$
plasmas, this will modify the threshold at which the pressure anisotropy is nonlinearly regulated (see §2.3 of Reference Sharma, Hammett, Quataert and StoneS06) and change the microphysical mechanism through which this regulation occurs (Sironi & Narayan Reference Sironi and Narayan2015).
Non-thermal distributions. Having focused on fluid models, we cannot address the many interesting questions surrounding non-thermal particle distributions that might develop. Strong non-thermal distributions have been seen in a variety of kinetic simulations (Riquelme et al. Reference Riquelme, Quataert, Sharma and Spitkovsky2012; Hoshino Reference Hoshino2015; Kunz et al. Reference Kunz, Stone and Quataert2016), perhaps due to magnetic reconnection.
Electrons. We have completely neglected any discussion of electron dynamics throughout this work. This can be loosely justified either when the electrons are (significantly) colder than ions, or in a weakly collisional regime, when ions dominate the anisotropic stress in the momentum equation due to the higher electron collisionality. However, even in such regimes, where the anisotropic stress due to elections is nominally subdominant to that of the ions, there may be additional subtleties induced by their thermodynamics. For example, the ion-cyclotron instability increases in importance compared to the mirror instability when
![]() $T_{e}\ll T_{i}$
(see above, Sironi & Narayan Reference Sironi and Narayan2015). Further, the induced electron-pressure-anisotropy stress will presumably not be efficiently regulated by ion-scale instabilities, potentially allowing the anisotropic electron stress to grow to dynamically important values even if
$T_{e}\ll T_{i}$
(see above, Sironi & Narayan Reference Sironi and Narayan2015). Further, the induced electron-pressure-anisotropy stress will presumably not be efficiently regulated by ion-scale instabilities, potentially allowing the anisotropic electron stress to grow to dynamically important values even if
![]() $T_{e}\ll T_{i}$
, and/or exciting electron instabilities (e.g. the electron whistler instability; Kim et al.
Reference Kim, Hwang, Seough and Yoon2017; Riquelme, Osorio & Quataert Reference Riquelme, Osorio and Quataert2017). In addition to the possible influence of electron-anisotropy instabilities and stresses, there are a variety of important questions to explore related to the proportion of viscous heating imparted to ions and electrons in RIAFs (e.g. see Sharma et al.
Reference Sharma, Quataert, Hammett and Stone2007, Ressler et al.
Reference Ressler, Tchekhovskoy, Quataert, Chandra and Gammie2015, Sironi Reference Sironi2015, Riquelme et al.
Reference Riquelme, Osorio and Quataert2017).
$T_{e}\ll T_{i}$
, and/or exciting electron instabilities (e.g. the electron whistler instability; Kim et al.
Reference Kim, Hwang, Seough and Yoon2017; Riquelme, Osorio & Quataert Reference Riquelme, Osorio and Quataert2017). In addition to the possible influence of electron-anisotropy instabilities and stresses, there are a variety of important questions to explore related to the proportion of viscous heating imparted to ions and electrons in RIAFs (e.g. see Sharma et al.
Reference Sharma, Quataert, Hammett and Stone2007, Ressler et al.
Reference Ressler, Tchekhovskoy, Quataert, Chandra and Gammie2015, Sironi Reference Sironi2015, Riquelme et al.
Reference Riquelme, Osorio and Quataert2017).
Non-gyrotropic effects. As the temporal and spatial scales of the MRI approach the gyro-scale, the approximation of gyrotropy – that the pressure tensor is symmetric about the magnetic-field lines – breaks down. In this case, either more complex fluid models (Passot, Sulem & Hunana Reference Passot, Sulem and Hunana2012) or fully kinetic treatments are needed to understand any key differences due to non-gyrotropic effects. While such effects are unlikely to be astrophysically important in current-epoch disks (where the separation between macroscopic scales and the gyro-scale is often
![]() ${\sim}10^{10}$
or more), they may be important for understanding the amplification of very weak (
${\sim}10^{10}$
or more), they may be important for understanding the amplification of very weak (
![]() $\unicode[STIX]{x1D6FD}\gtrsim \unicode[STIX]{x1D6FA}_{i}/\unicode[STIX]{x1D6FA}$
) fields in the high-redshift universe (Heinemann & Quataert Reference Heinemann and Quataert2014; Quataert et al.
Reference Quataert, Heinemann and Spitkovsky2015). In addition, numerical simulations will always have limited scale separations (in order to resolve both the macroscopic scales and the gyroradius), and knowledge of such effects could be important for the complex task of characterizing the limitations of kinetic simulations (see § 6.4).
$\unicode[STIX]{x1D6FD}\gtrsim \unicode[STIX]{x1D6FA}_{i}/\unicode[STIX]{x1D6FA}$
) fields in the high-redshift universe (Heinemann & Quataert Reference Heinemann and Quataert2014; Quataert et al.
Reference Quataert, Heinemann and Spitkovsky2015). In addition, numerical simulations will always have limited scale separations (in order to resolve both the macroscopic scales and the gyroradius), and knowledge of such effects could be important for the complex task of characterizing the limitations of kinetic simulations (see § 6.4).
6 Implications for the design of kinetic MRI turbulence simulations
In light of the above caveats concerning detailed kinetic effects absent in our models, it is clear that continued efforts to more rigorously simulate KMRI turbulence are needed. In this section, we leverage the results of this paper, as well as those from existing kinetic simulations of the KMRI and of Larmor-scale velocity-space instabilities, to provide some guidance for such efforts. Driving the discussion is a recognition that achieving a healthy scale separation in a kinetic simulation of magnetorotational turbulence is numerically expensive, perhaps prohibitively so. We thus focus primarily on non-asymptotic behaviour that might occur when
![]() $\unicode[STIX]{x1D6FA}/\unicode[STIX]{x1D6FA}_{i}$
is not sufficiently small, and provide some estimates for what
$\unicode[STIX]{x1D6FA}/\unicode[STIX]{x1D6FA}_{i}$
is not sufficiently small, and provide some estimates for what
![]() $\unicode[STIX]{x1D6FA}/\unicode[STIX]{x1D6FA}_{i}$
must be smaller than in order to capture the effects predicted in this paper. We stress that the asymptotic regime focused on in this paper is likely the most astrophysically relevant one, even if it is difficult to realize in fully kinetic simulations.
$\unicode[STIX]{x1D6FA}/\unicode[STIX]{x1D6FA}_{i}$
must be smaller than in order to capture the effects predicted in this paper. We stress that the asymptotic regime focused on in this paper is likely the most astrophysically relevant one, even if it is difficult to realize in fully kinetic simulations.
6.1 Pressure-anisotropy overshoot due to finite scale separation
First, in order for the mirror instability to effectively regulate the positive pressure anisotropy during the growth of KMRI, the growth of the mirrors must deplete the anisotropy faster than it is being adiabatically replenished by the KMRI. This requires
![]() $\unicode[STIX]{x1D6FE}_{m}/\unicode[STIX]{x1D6FE}_{\text{kmri}}>1$
, where
$\unicode[STIX]{x1D6FE}_{m}/\unicode[STIX]{x1D6FE}_{\text{kmri}}>1$
, where
![]() $\unicode[STIX]{x1D6FE}_{m}$
and
$\unicode[STIX]{x1D6FE}_{m}$
and
![]() $\unicode[STIX]{x1D6FE}_{\text{kmri}}$
are the growth rates of the mirror instability and KMRI, respectively. The maximum growth rate of the mirror instability is given by
$\unicode[STIX]{x1D6FE}_{\text{kmri}}$
are the growth rates of the mirror instability and KMRI, respectively. The maximum growth rate of the mirror instability is given by
![]() $\unicode[STIX]{x1D6FE}_{m}\sim \unicode[STIX]{x1D6FA}_{i}\unicode[STIX]{x1D6EC}_{m}^{2}$
, where
$\unicode[STIX]{x1D6FE}_{m}\sim \unicode[STIX]{x1D6FA}_{i}\unicode[STIX]{x1D6EC}_{m}^{2}$
, where
![]() $\unicode[STIX]{x1D6EC}_{m}\doteq \unicode[STIX]{x1D6E5}-1/\unicode[STIX]{x1D6FD}_{\bot }$
is positive when the plasma is mirror unstable (Hellinger Reference Hellinger2007). Thus, we require
$\unicode[STIX]{x1D6EC}_{m}\doteq \unicode[STIX]{x1D6E5}-1/\unicode[STIX]{x1D6FD}_{\bot }$
is positive when the plasma is mirror unstable (Hellinger Reference Hellinger2007). Thus, we require
![]() $\unicode[STIX]{x1D6EC}_{m}>(\unicode[STIX]{x1D6FE}_{\text{kmri}}/\unicode[STIX]{x1D6FA}_{i})^{1/2}$
for the mirror instability to outpace the KMRI-driven production of positive pressure anisotropy. For the vertical-field case,
$\unicode[STIX]{x1D6EC}_{m}>(\unicode[STIX]{x1D6FE}_{\text{kmri}}/\unicode[STIX]{x1D6FA}_{i})^{1/2}$
for the mirror instability to outpace the KMRI-driven production of positive pressure anisotropy. For the vertical-field case,
![]() $\unicode[STIX]{x1D6FE}_{\text{kmri}}=S/2$
at maximum growth, and so we require
$\unicode[STIX]{x1D6FE}_{\text{kmri}}=S/2$
at maximum growth, and so we require
![]() $\unicode[STIX]{x1D6EC}_{m}>(S/2\unicode[STIX]{x1D6FA}_{i})^{1/2}$
.Footnote
11
When there is an azimuthal magnetic field present,
$\unicode[STIX]{x1D6EC}_{m}>(S/2\unicode[STIX]{x1D6FA}_{i})^{1/2}$
.Footnote
11
When there is an azimuthal magnetic field present,
![]() $\unicode[STIX]{x1D6FE}_{\text{kmri}}\approx (2S\unicode[STIX]{x1D6FA})^{1/2}$
at maximum growth, and so we require
$\unicode[STIX]{x1D6FE}_{\text{kmri}}\approx (2S\unicode[STIX]{x1D6FA})^{1/2}$
at maximum growth, and so we require
![]() $\unicode[STIX]{x1D6EC}_{m}>(S/\unicode[STIX]{x1D6FA}_{i})^{1/2}\,(2\unicode[STIX]{x1D6FA}/S)^{1/4}\approx (S/\unicode[STIX]{x1D6FA}_{i})^{1/2}$
. Of course, in this case we must also contend with the firehose instability in regions where
$\unicode[STIX]{x1D6EC}_{m}>(S/\unicode[STIX]{x1D6FA}_{i})^{1/2}\,(2\unicode[STIX]{x1D6FA}/S)^{1/4}\approx (S/\unicode[STIX]{x1D6FA}_{i})^{1/2}$
. Of course, in this case we must also contend with the firehose instability in regions where
![]() $\unicode[STIX]{x1D6E5}\propto \unicode[STIX]{x1D6FF}B_{y}<0$
(see (3.6)), for which the instability criterion is
$\unicode[STIX]{x1D6E5}\propto \unicode[STIX]{x1D6FF}B_{y}<0$
(see (3.6)), for which the instability criterion is
![]() $\unicode[STIX]{x1D6EC}_{f}\doteq \unicode[STIX]{x1D6E5}+2/\unicode[STIX]{x1D6FD}_{\Vert }<0$
. With
$\unicode[STIX]{x1D6EC}_{f}\doteq \unicode[STIX]{x1D6E5}+2/\unicode[STIX]{x1D6FD}_{\Vert }<0$
. With
![]() $\unicode[STIX]{x1D6FE}_{f}\sim \unicode[STIX]{x1D6FA}_{i}|\unicode[STIX]{x1D6EC}_{f}|^{1/2}$
as the growth rate for the fastest-growing oblique firehose (Yoon et al.
Reference Yoon, Wu and de Assis1993; Hellinger & Matsumoto Reference Hellinger and Matsumoto2000), we require
$\unicode[STIX]{x1D6FE}_{f}\sim \unicode[STIX]{x1D6FA}_{i}|\unicode[STIX]{x1D6EC}_{f}|^{1/2}$
as the growth rate for the fastest-growing oblique firehose (Yoon et al.
Reference Yoon, Wu and de Assis1993; Hellinger & Matsumoto Reference Hellinger and Matsumoto2000), we require
![]() $|\unicode[STIX]{x1D6EC}_{f}|>(S/\unicode[STIX]{x1D6FA}_{i})^{2}\,(2\unicode[STIX]{x1D6FA}/S)\simeq (S/\unicode[STIX]{x1D6FA}_{i})^{2}$
for the firehose instability to outpace the KMRI-driven production of negative pressure anisotropy. The parallel-propagating firehose has
$|\unicode[STIX]{x1D6EC}_{f}|>(S/\unicode[STIX]{x1D6FA}_{i})^{2}\,(2\unicode[STIX]{x1D6FA}/S)\simeq (S/\unicode[STIX]{x1D6FA}_{i})^{2}$
for the firehose instability to outpace the KMRI-driven production of negative pressure anisotropy. The parallel-propagating firehose has
![]() $\unicode[STIX]{x1D6FE}_{f}=\unicode[STIX]{x1D6FA}_{i}|\unicode[STIX]{x1D6EC}_{f}|$
as its maximum growth rate (e.g. Davidson & Völk Reference Davidson and Völk1968; Rosin et al.
Reference Rosin, Schekochihin, Rincon and Cowley2011), and thus grows slower than its oblique counterpart for
$\unicode[STIX]{x1D6FE}_{f}=\unicode[STIX]{x1D6FA}_{i}|\unicode[STIX]{x1D6EC}_{f}|$
as its maximum growth rate (e.g. Davidson & Völk Reference Davidson and Völk1968; Rosin et al.
Reference Rosin, Schekochihin, Rincon and Cowley2011), and thus grows slower than its oblique counterpart for
![]() $|\unicode[STIX]{x1D6EC}_{f}|\lesssim 1$
.
$|\unicode[STIX]{x1D6EC}_{f}|\lesssim 1$
.
We now determine whether these criteria place prohibitive constraints on kinetic simulations. For the vertical-field KMRI,
![]() $\unicode[STIX]{x1D6E5}\sim (\unicode[STIX]{x1D6FF}B/B_{0})^{2}$
(see (3.2)), and so the mirror instability will grow fast enough to deplete the pressure anisotropy
$\unicode[STIX]{x1D6E5}\sim (\unicode[STIX]{x1D6FF}B/B_{0})^{2}$
(see (3.2)), and so the mirror instability will grow fast enough to deplete the pressure anisotropy
![]() $\unicode[STIX]{x1D6EC}_{m}\rightarrow 0^{+}$
when
$\unicode[STIX]{x1D6EC}_{m}\rightarrow 0^{+}$
when
beyond which the plasma is kept marginally mirror stable (and the results of this paper then follow). The asymptotic limit
![]() $(S/\unicode[STIX]{x1D6FA}_{i})\unicode[STIX]{x1D6FD}_{0}^{2}\rightarrow 0$
was taken throughout this paper to obtain
$(S/\unicode[STIX]{x1D6FA}_{i})\unicode[STIX]{x1D6FD}_{0}^{2}\rightarrow 0$
was taken throughout this paper to obtain
![]() $(\unicode[STIX]{x1D6FF}B/B_{0})^{2}\sim 1/\unicode[STIX]{x1D6FD}_{0}$
at the mirror instability threshold. The additional factor of
$(\unicode[STIX]{x1D6FF}B/B_{0})^{2}\sim 1/\unicode[STIX]{x1D6FD}_{0}$
at the mirror instability threshold. The additional factor of
![]() $(S/\unicode[STIX]{x1D6FA}_{i})^{1/2}$
due to overshoot beyond this threshold may be quite appreciable in a contemporary kinetic simulation of the MRI, perhaps
$(S/\unicode[STIX]{x1D6FA}_{i})^{1/2}$
due to overshoot beyond this threshold may be quite appreciable in a contemporary kinetic simulation of the MRI, perhaps
![]() ${\sim}0.1$
(e.g. Kunz et al.
Reference Kunz, Stone and Quataert2016) or even more (e.g. Riquelme et al.
Reference Riquelme, Quataert, Sharma and Spitkovsky2012; Hoshino Reference Hoshino2015), and thus might be comparable to, if not larger than,
${\sim}0.1$
(e.g. Kunz et al.
Reference Kunz, Stone and Quataert2016) or even more (e.g. Riquelme et al.
Reference Riquelme, Quataert, Sharma and Spitkovsky2012; Hoshino Reference Hoshino2015), and thus might be comparable to, if not larger than,
![]() $1/\unicode[STIX]{x1D6FD}_{0}$
. The situation will, of course, improve as the amplification of the magnetic-field strength by the KMRI increases
$1/\unicode[STIX]{x1D6FD}_{0}$
. The situation will, of course, improve as the amplification of the magnetic-field strength by the KMRI increases
![]() $\unicode[STIX]{x1D6FA}_{i}$
and decreases
$\unicode[STIX]{x1D6FA}_{i}$
and decreases
![]() $\unicode[STIX]{x1D6FD}$
. Thus, in the final, turbulent saturated state, the effect of finite scale separation will presumably be less severe than during the early, weakly nonlinear phases that have been the focus of this work; nonetheless, one should at least be aware of the impact of insufficient scale separation on the early phase of the KMRI.
$\unicode[STIX]{x1D6FD}$
. Thus, in the final, turbulent saturated state, the effect of finite scale separation will presumably be less severe than during the early, weakly nonlinear phases that have been the focus of this work; nonetheless, one should at least be aware of the impact of insufficient scale separation on the early phase of the KMRI.
In a mixed-azimuthal–vertical guide field, the KMRI-driven pressure anisotropy is linear in the mode amplitude (see (3.6)). Because, in this case, it is the pressure anisotropy which provides the azimuthal torque to transport angular momentum and drive the instability (rather than the magnetic tension), it matters all the more how efficiently the pressure anisotropy is regulated. If the lack of scale separation allows the pressure anisotropy to grow much beyond the mirror threshold, the instability’s behaviour once
![]() $\unicode[STIX]{x1D6FF}B_{y}\gtrsim \unicode[STIX]{x1D6FD}_{0}^{-2/3}B_{0y}$
may be completely different. Let us be quantitative, assuming
$\unicode[STIX]{x1D6FF}B_{y}\gtrsim \unicode[STIX]{x1D6FD}_{0}^{-2/3}B_{0y}$
may be completely different. Let us be quantitative, assuming
![]() $B_{0y}\approx B_{0z}$
and that
$B_{0y}\approx B_{0z}$
and that
![]() $\unicode[STIX]{x1D6FD}_{0}$
is sufficiently high (
$\unicode[STIX]{x1D6FD}_{0}$
is sufficiently high (
![]() $\unicode[STIX]{x1D6FD}_{0z}\gtrsim 10^{3}$
at least) that the scalings derived in appendix A hold. Then, the maximum growth rate of the azimuthal KMRI,
$\unicode[STIX]{x1D6FD}_{0z}\gtrsim 10^{3}$
at least) that the scalings derived in appendix A hold. Then, the maximum growth rate of the azimuthal KMRI,
![]() $\unicode[STIX]{x1D6FE}\approx (2S\unicode[STIX]{x03A9})^{1/2}$
, occurs at wavenumbers satisfying
$\unicode[STIX]{x1D6FE}\approx (2S\unicode[STIX]{x03A9})^{1/2}$
, occurs at wavenumbers satisfying
![]() $|k|v_{Az}/\unicode[STIX]{x1D6FA}\approx 2\unicode[STIX]{x1D6FD}_{0}^{-1/6}$
(see (A 2)), and the driven pressure anisotropy (3.6) is
$|k|v_{Az}/\unicode[STIX]{x1D6FA}\approx 2\unicode[STIX]{x1D6FD}_{0}^{-1/6}$
(see (A 2)), and the driven pressure anisotropy (3.6) is
where the final term in parentheses is order unity. Thus, the mirror instability will grow fast enough to deplete the excess positive pressure anisotropy when
which may be readily compared to (6.1). The asymptotic limit
![]() $(S/\unicode[STIX]{x1D6FA}_{i})\unicode[STIX]{x1D6FD}_{0}^{2}\rightarrow 0$
was taken throughout this paper to obtain
$(S/\unicode[STIX]{x1D6FA}_{i})\unicode[STIX]{x1D6FD}_{0}^{2}\rightarrow 0$
was taken throughout this paper to obtain
![]() $\unicode[STIX]{x1D6FF}B_{y}/B_{0}\sim \unicode[STIX]{x1D6FD}_{0}^{-2/3}$
at the mirror instability threshold. The additional factor of
$\unicode[STIX]{x1D6FF}B_{y}/B_{0}\sim \unicode[STIX]{x1D6FD}_{0}^{-2/3}$
at the mirror instability threshold. The additional factor of
![]() $(S/\unicode[STIX]{x1D6FA}_{i})^{1/2}\unicode[STIX]{x1D6FD}_{0}^{1/3}$
is due to the necessary overshoot beyond this threshold, which, again, may not be all that small in a contemporary kinetic simulation. For the firehose, the negative pressure anisotropy will be efficiently depleted when
$(S/\unicode[STIX]{x1D6FA}_{i})^{1/2}\unicode[STIX]{x1D6FD}_{0}^{1/3}$
is due to the necessary overshoot beyond this threshold, which, again, may not be all that small in a contemporary kinetic simulation. For the firehose, the negative pressure anisotropy will be efficiently depleted when
which will occur after the mirror criterion (6.3) is satisfied because of its more forgiving threshold (as long as
![]() $(S/\unicode[STIX]{x1D6FA}_{i})^{1/2}$
is small compared to
$(S/\unicode[STIX]{x1D6FA}_{i})^{1/2}$
is small compared to
![]() $1/\unicode[STIX]{x1D6FD}_{0}$
).
$1/\unicode[STIX]{x1D6FD}_{0}$
).
6.2 The impact of pressure-anisotropy overshoot on the KMRI
One notable impact of these pressure-anisotropy overshoots is on the fastest-growing KMRI-mode wavelength. For the vertical-field case, this wavelength will increase due to the nonlinear pressure anisotropy by an amount
![]() ${\approx}(3/2+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6EC}_{m}/2)^{1/2}$
. With
${\approx}(3/2+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6EC}_{m}/2)^{1/2}$
. With
![]() $\unicode[STIX]{x1D6EC}_{m}\gtrsim (S/\unicode[STIX]{x1D6FA}_{i})^{1/2}$
required for the mirrors to outpace the production of anisotropy, this could easily be a factor of several increase unless adequate scale separation is used. For example, having
$\unicode[STIX]{x1D6EC}_{m}\gtrsim (S/\unicode[STIX]{x1D6FA}_{i})^{1/2}$
required for the mirrors to outpace the production of anisotropy, this could easily be a factor of several increase unless adequate scale separation is used. For example, having
![]() $\unicode[STIX]{x1D6FD}=400$
and
$\unicode[STIX]{x1D6FD}=400$
and
![]() $S/\unicode[STIX]{x1D6FA}_{i}=0.01$
would result in a pressure-anisotropy-driven increase in the KMRI wavelength by a factor of
$S/\unicode[STIX]{x1D6FA}_{i}=0.01$
would result in a pressure-anisotropy-driven increase in the KMRI wavelength by a factor of
![]() ${\approx}5$
. In a computational box with vertical extent
${\approx}5$
. In a computational box with vertical extent
![]() $L_{z}\equiv c_{s}/\unicode[STIX]{x1D6FA}$
, this means that a maximally growing mode with
$L_{z}\equiv c_{s}/\unicode[STIX]{x1D6FA}$
, this means that a maximally growing mode with
![]() $kv_{A}\simeq \unicode[STIX]{x1D6FA}$
and
$kv_{A}\simeq \unicode[STIX]{x1D6FA}$
and
![]() $\unicode[STIX]{x1D6FE}\simeq S/2$
would shift from having
$\unicode[STIX]{x1D6FE}\simeq S/2$
would shift from having
![]() $\unicode[STIX]{x1D706}/L_{z}\approx 2\unicode[STIX]{x03C0}(2/\unicode[STIX]{x1D6FD})^{1/2}\approx 0.4$
to
$\unicode[STIX]{x1D706}/L_{z}\approx 2\unicode[STIX]{x03C0}(2/\unicode[STIX]{x1D6FD})^{1/2}\approx 0.4$
to
![]() $\unicode[STIX]{x1D706}/L_{z}\approx 2$
, bigger than the box. The mode’s wavelength would, of course, stop increasing once
$\unicode[STIX]{x1D706}/L_{z}\approx 2$
, bigger than the box. The mode’s wavelength would, of course, stop increasing once
![]() $\unicode[STIX]{x1D706}/L_{z}=1$
. But if, at that point,
$\unicode[STIX]{x1D706}/L_{z}=1$
. But if, at that point,
![]() $\unicode[STIX]{x1D6EC}_{m}\geqslant (S/\unicode[STIX]{x1D6FA})/2\unicode[STIX]{x03C0}^{2}-3/\unicode[STIX]{x1D6FD}$
, then all the KMRI modes in the box would be stabilized by the effectively increased magnetic tension. Since
$\unicode[STIX]{x1D6EC}_{m}\geqslant (S/\unicode[STIX]{x1D6FA})/2\unicode[STIX]{x03C0}^{2}-3/\unicode[STIX]{x1D6FD}$
, then all the KMRI modes in the box would be stabilized by the effectively increased magnetic tension. Since
![]() $\unicode[STIX]{x1D6EC}_{m}$
must grow to
$\unicode[STIX]{x1D6EC}_{m}$
must grow to
![]() ${\sim}(S/\unicode[STIX]{x1D6FA}_{i})^{1/2}$
before the mirrors can efficiently relax the pressure anisotropy and thereby remove some of this excess tension, we find that values of
${\sim}(S/\unicode[STIX]{x1D6FA}_{i})^{1/2}$
before the mirrors can efficiently relax the pressure anisotropy and thereby remove some of this excess tension, we find that values of
![]() $S/\unicode[STIX]{x1D6FA}_{i}\geqslant [(S/\unicode[STIX]{x1D6FA})/2\unicode[STIX]{x03C0}^{2}-3/\unicode[STIX]{x1D6FD}]^{2}$
will ultimately stabilize the KMRI.Footnote
12
It is, however, likely that this stabilization would be transient: even if the KMRI stops growing, the mirrors will continue relaxing
$S/\unicode[STIX]{x1D6FA}_{i}\geqslant [(S/\unicode[STIX]{x1D6FA})/2\unicode[STIX]{x03C0}^{2}-3/\unicode[STIX]{x1D6FD}]^{2}$
will ultimately stabilize the KMRI.Footnote
12
It is, however, likely that this stabilization would be transient: even if the KMRI stops growing, the mirrors will continue relaxing
![]() $\unicode[STIX]{x0394}p$
(albeit rather slowly), and at some point
$\unicode[STIX]{x0394}p$
(albeit rather slowly), and at some point
![]() $\unicode[STIX]{x0394}p$
would be sufficiently low so as to render the KMRI unstable again. Finally, we note that if the box does continue to support unstable KMRI modes on the largest scales
$\unicode[STIX]{x0394}p$
would be sufficiently low so as to render the KMRI unstable again. Finally, we note that if the box does continue to support unstable KMRI modes on the largest scales
![]() $\unicode[STIX]{x1D706}/L_{z}=1$
, one must ensure that the horizontal extent of the box is large enough to fit the parasitic modes (§ 4.1).
$\unicode[STIX]{x1D706}/L_{z}=1$
, one must ensure that the horizontal extent of the box is large enough to fit the parasitic modes (§ 4.1).
In the azimuthal–vertical-field case, the fastest-growing mode occurs on scales satisfying
![]() $kv_{Az}/\unicode[STIX]{x1D6FA}\sim \unicode[STIX]{x1D6FD}_{0}^{-1/6}$
, or
$kv_{Az}/\unicode[STIX]{x1D6FA}\sim \unicode[STIX]{x1D6FD}_{0}^{-1/6}$
, or
![]() $\unicode[STIX]{x1D706}/L_{z}\sim \unicode[STIX]{x1D6FD}_{0}^{-1/3}$
. These scales are larger than those of the standard MRI and the vertical-field KMRI. We have predicted that, as the mirror and firehose instabilities kick in and regulate the pressure anisotropy, the influence of the
$\unicode[STIX]{x1D706}/L_{z}\sim \unicode[STIX]{x1D6FD}_{0}^{-1/3}$
. These scales are larger than those of the standard MRI and the vertical-field KMRI. We have predicted that, as the mirror and firehose instabilities kick in and regulate the pressure anisotropy, the influence of the
![]() $\unicode[STIX]{x1D6FF}p_{\bot }$
and
$\unicode[STIX]{x1D6FF}p_{\bot }$
and
![]() $\unicode[STIX]{x1D6FF}p_{\Vert }$
perturbations on the mode evolution is suppressed and the KMRI reverts back to its standard, MHD-like behaviour. This involves a suppression of long-wavelength MRI modes (i.e.
$\unicode[STIX]{x1D6FF}p_{\Vert }$
perturbations on the mode evolution is suppressed and the KMRI reverts back to its standard, MHD-like behaviour. This involves a suppression of long-wavelength MRI modes (i.e.
![]() $\unicode[STIX]{x1D6FE}_{\text{kmri}}$
decreases for
$\unicode[STIX]{x1D6FE}_{\text{kmri}}$
decreases for
![]() $kv_{A}\lesssim 1$
) and a transition phase in the nonlinear evolution (‘Region 2’ in figure 3
a), in which the mode becomes more MHD-like at smaller scales with the kinetic and magnetic energies in approximate equipartition. If the mirror regularization is especially sluggish due to inadequate scale separation, this phase might be skipped altogether and a
$kv_{A}\lesssim 1$
) and a transition phase in the nonlinear evolution (‘Region 2’ in figure 3
a), in which the mode becomes more MHD-like at smaller scales with the kinetic and magnetic energies in approximate equipartition. If the mirror regularization is especially sluggish due to inadequate scale separation, this phase might be skipped altogether and a
![]() $\unicode[STIX]{x1D706}/L_{z}=1$
mode will take the place of what is instead seen in figure 3(b). It is also worth noting that the large value of
$\unicode[STIX]{x1D706}/L_{z}=1$
mode will take the place of what is instead seen in figure 3(b). It is also worth noting that the large value of
![]() $\unicode[STIX]{x1D6FD}_{0}=5000$
used in § 3.3 to accentuate the different regions of evolution would require an especially small value of
$\unicode[STIX]{x1D6FD}_{0}=5000$
used in § 3.3 to accentuate the different regions of evolution would require an especially small value of
![]() $S/\unicode[STIX]{x1D6FA}_{i}$
in a kinetic simulation.
$S/\unicode[STIX]{x1D6FA}_{i}$
in a kinetic simulation.
6.3 The microphysics of the firehose and mirror instabilities
A further constraint on the choice of
![]() $S/\unicode[STIX]{x1D6FA}_{i}$
concerns the means by which mirror/firehose instabilities regulate the pressure anisotropy. In order for these instabilities to efficiently keep the anisotropy near the instability thresholds via the anomalous pitch-angle scattering of particles, the scattering rate must be
$S/\unicode[STIX]{x1D6FA}_{i}$
concerns the means by which mirror/firehose instabilities regulate the pressure anisotropy. In order for these instabilities to efficiently keep the anisotropy near the instability thresholds via the anomalous pitch-angle scattering of particles, the scattering rate must be
![]() ${\sim}S\unicode[STIX]{x1D6FD}$
, and this number must be smaller than
${\sim}S\unicode[STIX]{x1D6FD}$
, and this number must be smaller than
![]() $\unicode[STIX]{x1D6FA}_{i}$
.
$\unicode[STIX]{x1D6FA}_{i}$
.
In the case of the firehose instability, when
![]() $S/\unicode[STIX]{x1D6FA}_{i}\ll 1/\unicode[STIX]{x1D6FD}$
the firehose fluctuations saturate at a mean level
$S/\unicode[STIX]{x1D6FA}_{i}\ll 1/\unicode[STIX]{x1D6FD}$
the firehose fluctuations saturate at a mean level
![]() $\langle |\unicode[STIX]{x1D6FF}\boldsymbol{B}/B|^{2}\rangle \sim (\unicode[STIX]{x1D6FD}S/\unicode[STIX]{x1D6FA}_{i})^{1/2}$
in a time
$\langle |\unicode[STIX]{x1D6FF}\boldsymbol{B}/B|^{2}\rangle \sim (\unicode[STIX]{x1D6FD}S/\unicode[STIX]{x1D6FA}_{i})^{1/2}$
in a time
![]() ${\sim}[\unicode[STIX]{x1D6FD}/(S\unicode[STIX]{x1D6FA}_{i})]^{1/2}\ll S^{-1}\sim \unicode[STIX]{x1D6FE}_{\text{kmri}}^{-1}$
(Kunz et al.
Reference Kunz, Schekochihin and Stone2014a
; Melville et al.
Reference Melville, Schekochihin and Kunz2016). This is achieved via pitch-angle scattering of the particles off Larmor-scale firehose fluctuations, which precludes the adiabatic production of pressure anisotropy. In this limit, since local shear in a macroscopic plasma flow will change in time at the rate comparable to the shear itself, one can safely consider the anomalous collisionality associated with the firehose fluctuations to turn on instantaneously, in line with the macroscopic modelling assumption used in this paper. At sufficiently high
${\sim}[\unicode[STIX]{x1D6FD}/(S\unicode[STIX]{x1D6FA}_{i})]^{1/2}\ll S^{-1}\sim \unicode[STIX]{x1D6FE}_{\text{kmri}}^{-1}$
(Kunz et al.
Reference Kunz, Schekochihin and Stone2014a
; Melville et al.
Reference Melville, Schekochihin and Kunz2016). This is achieved via pitch-angle scattering of the particles off Larmor-scale firehose fluctuations, which precludes the adiabatic production of pressure anisotropy. In this limit, since local shear in a macroscopic plasma flow will change in time at the rate comparable to the shear itself, one can safely consider the anomalous collisionality associated with the firehose fluctuations to turn on instantaneously, in line with the macroscopic modelling assumption used in this paper. At sufficiently high
![]() $\unicode[STIX]{x1D6FD}$
and/or
$\unicode[STIX]{x1D6FD}$
and/or
![]() $S$
such that
$S$
such that
![]() $\unicode[STIX]{x1D6FD}\gtrsim \unicode[STIX]{x1D6FA}_{i}/S$
, however, this is no longer true and the firehose fluctuations saturate at an order-unity level independent of either
$\unicode[STIX]{x1D6FD}\gtrsim \unicode[STIX]{x1D6FA}_{i}/S$
, however, this is no longer true and the firehose fluctuations saturate at an order-unity level independent of either
![]() $\unicode[STIX]{x1D6FD}$
or
$\unicode[STIX]{x1D6FD}$
or
![]() $S$
, after growing secularly without scattering particles for one shear time (Melville et al.
Reference Melville, Schekochihin and Kunz2016). Thus, for kinetic simulations of MRI turbulence to reliably demonstrate the anomalous-scattering model of pressure-anisotropy regulation used in this work and others (e.g. Sharma et al.
Reference Sharma, Hammett, Quataert and Stone2006; Mogavero & Schekochihin Reference Mogavero and Schekochihin2014; Santos-Lima et al.
Reference Santos-Lima, de Gouveia Dal Pino, Kowal, Falceta-Gonçalves, Lazarian and Nakwacki2014; Chandra et al.
Reference Chandra, Gammie, Foucart and Quataert2015; Foucart et al.
Reference Foucart, Chandra, Gammie and Quataert2015), parameters must be chosen such that
$S$
, after growing secularly without scattering particles for one shear time (Melville et al.
Reference Melville, Schekochihin and Kunz2016). Thus, for kinetic simulations of MRI turbulence to reliably demonstrate the anomalous-scattering model of pressure-anisotropy regulation used in this work and others (e.g. Sharma et al.
Reference Sharma, Hammett, Quataert and Stone2006; Mogavero & Schekochihin Reference Mogavero and Schekochihin2014; Santos-Lima et al.
Reference Santos-Lima, de Gouveia Dal Pino, Kowal, Falceta-Gonçalves, Lazarian and Nakwacki2014; Chandra et al.
Reference Chandra, Gammie, Foucart and Quataert2015; Foucart et al.
Reference Foucart, Chandra, Gammie and Quataert2015), parameters must be chosen such that
![]() $S/\unicode[STIX]{x1D6FA}_{i}<1/\unicode[STIX]{x1D6FD}$
, preferably by a decade or more. Again, satisfying this inequality becomes easier as the KMRI grows the magnetic-field strength. But, for the early phases of evolution, this cautions against setting
$S/\unicode[STIX]{x1D6FA}_{i}<1/\unicode[STIX]{x1D6FD}$
, preferably by a decade or more. Again, satisfying this inequality becomes easier as the KMRI grows the magnetic-field strength. But, for the early phases of evolution, this cautions against setting
![]() $\unicode[STIX]{x1D6FD}_{0}$
too high, because this will impose stiff constraints on an acceptable value of
$\unicode[STIX]{x1D6FD}_{0}$
too high, because this will impose stiff constraints on an acceptable value of
![]() $S/\unicode[STIX]{x1D6FA}_{i0}$
.
$S/\unicode[STIX]{x1D6FA}_{i0}$
.
In the arguably more relevant case of the mirror instability, when
![]() $S/\unicode[STIX]{x1D6FA}_{i}\ll 1/\unicode[STIX]{x1D6FD}$
the mirror fluctuations saturate at a mean level
$S/\unicode[STIX]{x1D6FA}_{i}\ll 1/\unicode[STIX]{x1D6FD}$
the mirror fluctuations saturate at a mean level
![]() $\langle (\unicode[STIX]{x1D6FF}B/B)^{2}\rangle \sim 1$
in a time
$\langle (\unicode[STIX]{x1D6FF}B/B)^{2}\rangle \sim 1$
in a time
![]() ${\sim}S^{-1}\sim \unicode[STIX]{x1D6FE}_{\text{kmri}}^{-1}$
(Kunz et al.
Reference Kunz, Schekochihin and Stone2014a
; Riquelme et al.
Reference Riquelme, Quataert and Verscharen2015; Melville et al.
Reference Melville, Schekochihin and Kunz2016). While marginal stability and mirror saturation is ultimately achieved via pitch-angle scattering of the particles off Larmor-scale bends at the ends of the magnetic mirrors, there is a long (
${\sim}S^{-1}\sim \unicode[STIX]{x1D6FE}_{\text{kmri}}^{-1}$
(Kunz et al.
Reference Kunz, Schekochihin and Stone2014a
; Riquelme et al.
Reference Riquelme, Quataert and Verscharen2015; Melville et al.
Reference Melville, Schekochihin and Kunz2016). While marginal stability and mirror saturation is ultimately achieved via pitch-angle scattering of the particles off Larmor-scale bends at the ends of the magnetic mirrors, there is a long (
![]() ${\sim}S^{-1}$
) phase in which the pressure anisotropy is held marginal without appreciable particle scattering. This is achieved by corralling an ever increasing number of particles into the deepening magnetic wells, in which these particles become trapped, approximately conserve their
${\sim}S^{-1}$
) phase in which the pressure anisotropy is held marginal without appreciable particle scattering. This is achieved by corralling an ever increasing number of particles into the deepening magnetic wells, in which these particles become trapped, approximately conserve their
![]() $\unicode[STIX]{x1D707}$
as they bounce to and fro, and perceive no average change in
$\unicode[STIX]{x1D707}$
as they bounce to and fro, and perceive no average change in
![]() $B$
(and thus no generation of net pressure anisotropy) along their bounce orbits. The increase in the large-scale
$B$
(and thus no generation of net pressure anisotropy) along their bounce orbits. The increase in the large-scale
![]() $B$
is offset by the decrease in the intra-mirror
$B$
is offset by the decrease in the intra-mirror
![]() $B$
. During this phase of evolution, the mirror fluctuations grow at the rate required to offset the production of pressure anisotropy by the KMRI-driven growth in the large-scale magnetic-field strength. A few things must be satisfied for kinetic simulations of KMRI growth to produce results similar to those predicted in this paper. First, the hard-wall limiter on the pressure anisotropy that we (and others) use must be an adequate (if not complete) representation of the otherwise more complicated mirror-driven regulation. This is particularly true during the
$B$
. During this phase of evolution, the mirror fluctuations grow at the rate required to offset the production of pressure anisotropy by the KMRI-driven growth in the large-scale magnetic-field strength. A few things must be satisfied for kinetic simulations of KMRI growth to produce results similar to those predicted in this paper. First, the hard-wall limiter on the pressure anisotropy that we (and others) use must be an adequate (if not complete) representation of the otherwise more complicated mirror-driven regulation. This is particularly true during the
![]() $\unicode[STIX]{x1D707}$
-conserving phase of the mirror instability: does it matter to the large (i.e. KMRI) scales that an ever-increasing population of trapped particles are ignorant of the KMRI-driven magnetic-field growth during this phase? If not, then fine; simply limit the pressure anisotropy at the mirror instability using an enhanced collisionality, nothing more sophisticated being necessary. But, if so, then an effort must be made in the kinetic simulation to ensure that its results, if different from those predicted in this paper, are truly asymptotic. Namely, since the
$\unicode[STIX]{x1D707}$
-conserving phase of the mirror instability: does it matter to the large (i.e. KMRI) scales that an ever-increasing population of trapped particles are ignorant of the KMRI-driven magnetic-field growth during this phase? If not, then fine; simply limit the pressure anisotropy at the mirror instability using an enhanced collisionality, nothing more sophisticated being necessary. But, if so, then an effort must be made in the kinetic simulation to ensure that its results, if different from those predicted in this paper, are truly asymptotic. Namely, since the
![]() $\unicode[STIX]{x1D707}$
-conserving phase of the mirror instability lasts just one shear time, whereas the KMRI growth phase typically lasts several shear times, there must be enough scale separation so that the mirrors can saturate before
$\unicode[STIX]{x1D707}$
-conserving phase of the mirror instability lasts just one shear time, whereas the KMRI growth phase typically lasts several shear times, there must be enough scale separation so that the mirrors can saturate before
![]() $\unicode[STIX]{x1D6FF}B/B_{0}$
of the KMRI enters into the nonlinear phases we predicted in § 3. Secondly, do the Larmor-scale mirror distortions in the magnetic-field direction greatly affect the efficacy of the heat flow? An answer in the affirmative is suggested by Komarov et al. (Reference Komarov, Churazov, Kunz and Schekochihin2016), Riquelme et al. (Reference Riquelme, Quataert and Verscharen2016), Riquelme et al. (Reference Riquelme, Quataert and Verscharen2017). But, if the effect of these distortions is simply a reduction in the magnitude of the heat flow, then the footnote in § 2.1 applies: our results are not strongly affected. The reason is that, by the time the mirror instability is triggered, the heat flows have already spatially smoothed the pressure anisotropy on the scale of the KMRI mode, fulfilling their main role in influencing the mode evolution.
$\unicode[STIX]{x1D6FF}B/B_{0}$
of the KMRI enters into the nonlinear phases we predicted in § 3. Secondly, do the Larmor-scale mirror distortions in the magnetic-field direction greatly affect the efficacy of the heat flow? An answer in the affirmative is suggested by Komarov et al. (Reference Komarov, Churazov, Kunz and Schekochihin2016), Riquelme et al. (Reference Riquelme, Quataert and Verscharen2016), Riquelme et al. (Reference Riquelme, Quataert and Verscharen2017). But, if the effect of these distortions is simply a reduction in the magnitude of the heat flow, then the footnote in § 2.1 applies: our results are not strongly affected. The reason is that, by the time the mirror instability is triggered, the heat flows have already spatially smoothed the pressure anisotropy on the scale of the KMRI mode, fulfilling their main role in influencing the mode evolution.
6.4 Finite-Larmor-radius effects
There is additional physics that enters when
![]() $S/\unicode[STIX]{x1D6FA}_{i}$
is not sufficiently small, which might complicate the evolution of the KMRI beyond that envisaged herein. First, gyroviscous effects become important when
$S/\unicode[STIX]{x1D6FA}_{i}$
is not sufficiently small, which might complicate the evolution of the KMRI beyond that envisaged herein. First, gyroviscous effects become important when
![]() $\unicode[STIX]{x1D6FD}\gtrsim 4\unicode[STIX]{x1D6FA}_{i}/\unicode[STIX]{x1D6FA}$
(Ferraro Reference Ferraro2007; Heinemann & Quataert Reference Heinemann and Quataert2014). For such
$\unicode[STIX]{x1D6FD}\gtrsim 4\unicode[STIX]{x1D6FA}_{i}/\unicode[STIX]{x1D6FA}$
(Ferraro Reference Ferraro2007; Heinemann & Quataert Reference Heinemann and Quataert2014). For such
![]() $\unicode[STIX]{x1D6FD}$
, the polarity of the mean magnetic field influences the stability and MRI growth rates. Without a good scale separation between
$\unicode[STIX]{x1D6FD}$
, the polarity of the mean magnetic field influences the stability and MRI growth rates. Without a good scale separation between
![]() $\unicode[STIX]{x1D6FA}$
and
$\unicode[STIX]{x1D6FA}$
and
![]() $\unicode[STIX]{x1D6FA}_{i}$
, finite-Larmor-radius effects might therefore artificially modify the KMRI, even at modest
$\unicode[STIX]{x1D6FA}_{i}$
, finite-Larmor-radius effects might therefore artificially modify the KMRI, even at modest
![]() $\unicode[STIX]{x1D6FD}$
. Secondly, note that an equilibrium particle distribution function in a strongly magnetized differentially rotating disc can be quite different than an equilibrium distribution function in an unmagnetized disc. In the latter, a tidal anisotropy of the in-plane thermal motions of the particles is enforced by epicyclic motion in the rotational supported plasma (see § 3.1 of Heinemann & Quataert Reference Heinemann and Quataert2014); this effect goes away in a strongly magnetized plasma, where gyrotropy of the distribution function about the magnetic field is enforced. This is important because, if the initial magnetic field is inclined with respect to the rotation axis (i.e.
$\unicode[STIX]{x1D6FD}$
. Secondly, note that an equilibrium particle distribution function in a strongly magnetized differentially rotating disc can be quite different than an equilibrium distribution function in an unmagnetized disc. In the latter, a tidal anisotropy of the in-plane thermal motions of the particles is enforced by epicyclic motion in the rotational supported plasma (see § 3.1 of Heinemann & Quataert Reference Heinemann and Quataert2014); this effect goes away in a strongly magnetized plasma, where gyrotropy of the distribution function about the magnetic field is enforced. This is important because, if the initial magnetic field is inclined with respect to the rotation axis (i.e.
![]() $b_{y}\neq 0$
,
$b_{y}\neq 0$
,
![]() $b_{z}\neq 1$
) and
$b_{z}\neq 1$
) and
![]() $S/\unicode[STIX]{x1D6FA}_{i}$
is not sufficiently small, this tidal anisotropy can function as a field-biased pressure anisotropy and potentially drive mirror fluctuations in the equilibrium state. To wit, the equilibrium field-biased pressure anisotropy is
$S/\unicode[STIX]{x1D6FA}_{i}$
is not sufficiently small, this tidal anisotropy can function as a field-biased pressure anisotropy and potentially drive mirror fluctuations in the equilibrium state. To wit, the equilibrium field-biased pressure anisotropy is
![]() $\unicode[STIX]{x1D6E5}\approx (3/2)(S/\unicode[STIX]{x1D6FA}_{i})(b_{y}^{2}-1/3)/b_{z}$
to leading order in
$\unicode[STIX]{x1D6E5}\approx (3/2)(S/\unicode[STIX]{x1D6FA}_{i})(b_{y}^{2}-1/3)/b_{z}$
to leading order in
![]() $S/\unicode[STIX]{x1D6FA}_{i}$
when
$S/\unicode[STIX]{x1D6FA}_{i}$
when
![]() $b_{z}\neq 0$
. A disc with
$b_{z}\neq 0$
. A disc with
![]() $b_{y}=b_{z}=1/\sqrt{2}$
would be mirror unstable from the tidal anisotropy alone if
$b_{y}=b_{z}=1/\sqrt{2}$
would be mirror unstable from the tidal anisotropy alone if
![]() $S/\unicode[STIX]{x1D6FA}_{i}\gtrsim 2\sqrt{2}\unicode[STIX]{x1D6FD}^{-1}$
. (A plasma with, say,
$S/\unicode[STIX]{x1D6FA}_{i}\gtrsim 2\sqrt{2}\unicode[STIX]{x1D6FD}^{-1}$
. (A plasma with, say,
![]() $\unicode[STIX]{x1D6FD}_{0}=400$
and
$\unicode[STIX]{x1D6FD}_{0}=400$
and
![]() $S/\unicode[STIX]{x1D6FA}_{i}=0.01$
would thus be mirror unstable, even without the KMRI-driven pressure anisotropy.) If the background field is exactly azimuthal, then the field-biased pressure anisotropy
$S/\unicode[STIX]{x1D6FA}_{i}=0.01$
would thus be mirror unstable, even without the KMRI-driven pressure anisotropy.) If the background field is exactly azimuthal, then the field-biased pressure anisotropy
![]() $\unicode[STIX]{x1D6E5}=S/(2\unicode[STIX]{x1D6FA})>0$
, and any large-
$\unicode[STIX]{x1D6E5}=S/(2\unicode[STIX]{x1D6FA})>0$
, and any large-
![]() $\unicode[STIX]{x1D6FD}$
plasma would be trivially mirror unstable, no matter how strongly the plasma is magnetized.
$\unicode[STIX]{x1D6FD}$
plasma would be trivially mirror unstable, no matter how strongly the plasma is magnetized.
6.5 The saturated state
Finally, one must be cognizant of the physical constraints and computational demands not only during the early stages of the KMRI, but also in the saturated state. In going, say, from
![]() $\unicode[STIX]{x1D6FD}_{0}\approx 10^{3}$
to
$\unicode[STIX]{x1D6FD}_{0}\approx 10^{3}$
to
![]() $\unicode[STIX]{x1D6FD}\approx 4$
, as often seen in a typical magnetorotationally turbulent saturated state (e.g. Pessah, Chan & Psaltis Reference Pessah, Chan and Psaltis2006), the ion Larmor radius might shrink by a factor between
$\unicode[STIX]{x1D6FD}\approx 4$
, as often seen in a typical magnetorotationally turbulent saturated state (e.g. Pessah, Chan & Psaltis Reference Pessah, Chan and Psaltis2006), the ion Larmor radius might shrink by a factor between
![]() ${\approx}4$
(if
${\approx}4$
(if
![]() $\unicode[STIX]{x1D707}$
is somehow conserved during this process) and
$\unicode[STIX]{x1D707}$
is somehow conserved during this process) and
![]() ${\approx}16$
(if
${\approx}16$
(if
![]() $\unicode[STIX]{x1D707}$
is not). Increased scale separation is, of course, a good thing, but only to a point. If
$\unicode[STIX]{x1D707}$
is not). Increased scale separation is, of course, a good thing, but only to a point. If
![]() $\unicode[STIX]{x1D70C}_{i}$
decreases so much that it falls under the numerical grid, then the anomalous particle scattering from ion-Larmor-scale magnetic structures that plays a regulatory role for the pressure anisotropy will be attenuated, fundamentally changing the physics of the mirror and firehose instabilities.
$\unicode[STIX]{x1D70C}_{i}$
decreases so much that it falls under the numerical grid, then the anomalous particle scattering from ion-Larmor-scale magnetic structures that plays a regulatory role for the pressure anisotropy will be attenuated, fundamentally changing the physics of the mirror and firehose instabilities.
7 Conclusions
A persistent feature of high-
![]() $\unicode[STIX]{x1D6FD}$
collisionless plasmas is the appearance of nonlinearity due to pressure anisotropy in regimes where similar dynamics in a collisional (MHD) plasma is linear (e.g. Schekochihin & Cowley Reference Schekochihin and Cowley2006, Mogavero & Schekochihin Reference Mogavero and Schekochihin2014, Squire et al.
Reference Squire, Quataert and Schekochihin2016). Such behaviour generically arises because, for similar values of the magnetic field, the mechanisms that generate a pressure anisotropy are proportional to the total pressure (e.g.
$\unicode[STIX]{x1D6FD}$
collisionless plasmas is the appearance of nonlinearity due to pressure anisotropy in regimes where similar dynamics in a collisional (MHD) plasma is linear (e.g. Schekochihin & Cowley Reference Schekochihin and Cowley2006, Mogavero & Schekochihin Reference Mogavero and Schekochihin2014, Squire et al.
Reference Squire, Quataert and Schekochihin2016). Such behaviour generically arises because, for similar values of the magnetic field, the mechanisms that generate a pressure anisotropy are proportional to the total pressure (e.g.
![]() $\text{d}\unicode[STIX]{x0394}p/\text{d}t\sim p_{0}\,\text{d}\ln B/\text{d}t$
in the collisionless case), while the momentum stresses induced by this anisotropy (i.e. its dynamical effects) depend on
$\text{d}\unicode[STIX]{x0394}p/\text{d}t\sim p_{0}\,\text{d}\ln B/\text{d}t$
in the collisionless case), while the momentum stresses induced by this anisotropy (i.e. its dynamical effects) depend on
![]() $\unicode[STIX]{x0394}p$
itself (i.e. not on
$\unicode[STIX]{x0394}p$
itself (i.e. not on
![]() $\unicode[STIX]{x0394}p/p_{0}$
). Thus a larger background pressure leads to larger anisotropic stresses, which dominate the Lorentz force by a factor
$\unicode[STIX]{x0394}p/p_{0}$
). Thus a larger background pressure leads to larger anisotropic stresses, which dominate the Lorentz force by a factor
![]() ${\sim}\unicode[STIX]{x1D6FD}$
. This implies that nonlinear effects can become important for very small changes in magnetic-field strength. However, as is well known, once the anisotropy grows beyond
${\sim}\unicode[STIX]{x1D6FD}$
. This implies that nonlinear effects can become important for very small changes in magnetic-field strength. However, as is well known, once the anisotropy grows beyond
![]() $\unicode[STIX]{x0394}p\sim \pm B^{2}$
, the firehose and mirror instabilities grow rapidly at ion gyro-scales and limit any further growth in
$\unicode[STIX]{x0394}p\sim \pm B^{2}$
, the firehose and mirror instabilities grow rapidly at ion gyro-scales and limit any further growth in
![]() $\unicode[STIX]{x0394}p$
. We are then left with the question of whether the resulting dynamics on large scales is effectively MHD-like (as occurs if the microinstability-limited
$\unicode[STIX]{x0394}p$
. We are then left with the question of whether the resulting dynamics on large scales is effectively MHD-like (as occurs if the microinstability-limited
![]() $\unicode[STIX]{x0394}p$
is dynamically unimportant), or whether there are strong differences compared to MHD. In either case, we can expect that linear instabilities will be nonlinearly modified for amplitudes well below where such modifications occur in MHD.
$\unicode[STIX]{x0394}p$
is dynamically unimportant), or whether there are strong differences compared to MHD. In either case, we can expect that linear instabilities will be nonlinearly modified for amplitudes well below where such modifications occur in MHD.
This work has considered the influence of this physics on the collisionless (kinetic) and weakly collisional (Braginskii) magnetorotational instability (KMRI), focusing on the characteristics of the instability at high
![]() $\unicode[STIX]{x1D6FD}$
before its saturation into turbulence. Our general motivations have been to:
$\unicode[STIX]{x1D6FD}$
before its saturation into turbulence. Our general motivations have been to:
-
(i) Understand if there are any alternate (pressure anisotropy related) means for the linear KMRI to saturate in various regimes. Such a mechanism could significantly alter expected angular-momentum transport properties of kinetic MRI turbulence.
-
(ii) Inform current and future kinetic numerical simulations of the KMRI – which are complex, computationally expensive and difficult to analyse – on some key differences and similarities as compared to well-known MHD results.
Our main finding is that the KMRI at large amplitudes behaves quite similarly to the standard (MHD) MRI. In fact, in some cases – in particular, the MRI in a mean azimuthal–vertical field (also known as the magnetoviscous instability) – the MRI transitions from kinetic to MHD-like behaviour as its amplitude increases. Furthermore, in all cases studied we have seen the channel mode (
![]() $k_{x}=k_{y}=0$
MRI mode) emerge as an approximate nonlinear solution of the kinetic equations at large amplitudes, in the same way as occurs in MHD (Goodman & Xu Reference Goodman and Xu1994). This is because the mirror-limited pressure anisotropy has the same form as the Lorentz force (since
$k_{x}=k_{y}=0$
MRI mode) emerge as an approximate nonlinear solution of the kinetic equations at large amplitudes, in the same way as occurs in MHD (Goodman & Xu Reference Goodman and Xu1994). This is because the mirror-limited pressure anisotropy has the same form as the Lorentz force (since
![]() $\unicode[STIX]{x0394}p\propto B^{2}$
), and this vanishes identically for an MRI channel mode. This points to an interesting robustness of the channel-mode solution in collisionless plasmas that had not been previously fully appreciated.
$\unicode[STIX]{x0394}p\propto B^{2}$
), and this vanishes identically for an MRI channel mode. This points to an interesting robustness of the channel-mode solution in collisionless plasmas that had not been previously fully appreciated.
The similarity between the nonlinear physics of the KMRI and the MHD MRI is certainly not a given; for example, the nonlinear dynamics of shear Alfvén waves, which is related to the MRI (Balbus & Hawley Reference Balbus and Hawley1998), differs very significantly between collisional and kinetic plasmas (Squire et al. Reference Squire, Quataert and Schekochihin2016, Reference Squire, Schekochihin and Quataert2017). Further, there remain a variety of 1-D nonlinear effects that cause modest differences when compared to standard MHD, and these could be important for the difficult task of designing and interpreting 3-D fully kinetic simulations. For example, depending on the level of overshoot of the pressure anisotropy above the mirror instability threshold (as would occur if there were insufficient scale separation between the large-scale dynamics and the gyro-scale; see § 6), the MRI mode may migrate to longer wavelengths at moderate amplitudes, or (in extreme cases) be completely stabilized. A more detailed overview of the most relevant 1-D results is given in § 3.4.
Motivated by the finding that there are no viable 1-D mechanisms for halting the growth of the kinetic MRI, as also found in previous numerical simulations (Reference Sharma, Hammett, Quataert and StoneS06; Sharma et al. Reference Sharma, Quataert, Hammett and Stone2007, Riquelme et al. Reference Riquelme, Quataert, Sharma and Spitkovsky2012, Kunz et al. Reference Kunz, Stone and Bai2014b , Hoshino Reference Hoshino2015), we are left with the conclusion that 3-D effects must govern the collapse of a KMRI channel mode into a turbulent-like state. Following previous MHD studies (Goodman & Xu Reference Goodman and Xu1994; Latter et al. Reference Latter, Lesaffre and Balbus2009; Pessah & Goodman Reference Pessah and Goodman2009), we have considered 3-D mechanisms for mode saturation in terms of parasitic modes, secondary instabilities that feed off the large field and flow gradients of the channel mode, acting to disrupt it and cause its collapse into turbulence. Using both linear studies of parasitic modes and 3-D nonlinear simulations (with the modified Zeus version of Reference Sharma, Hammett, Quataert and StoneS06), we have found very little difference between the behaviour of parasitic modes in kinetic and MHD models. We have further shown that the observations of Reference Sharma, Hammett, Quataert and StoneS06 of larger saturation amplitudes in kinetic models as compared to MHD may be straightforwardly explained by the migration of kinetic channel modes to longer wavelengths due to the mean pressure anisotropy (i.e. 1-D effects). This suggests that MHD results may be used to give simple, zeroth-order estimates of the expected amplitude at which a KMRI channel mode should saturate into turbulence. Similar conclusions have also been found in global Braginskii MHD simulations of accretion disks (Foucart et al. Reference Foucart, Chandra, Gammie, Quataert and Tchekhovskoy2017).
Although our results suggest that the breakdown into turbulence occurs in a similar way in kinetic theory and MHD, this does not necessarily imply that the saturated state of the turbulence is similar. Indeed, even following the pioneering 3-D nonlinear kinetic MRI simulations of Hoshino (Reference Hoshino2015) and Kunz et al. (Reference Kunz, Stone and Quataert2016), many properties of the saturated state of the KMRI – i.e. the turbulence – remain largely unknown. The zero-net-flux simulation of Kunz et al. (Reference Kunz, Stone and Quataert2016) found a level of turbulence that was comparable to high-Prandtl-number turbulence in MHD. However, there are some notable differences; for instance, a greater prevalence of coherent flows, and the fact that (in contrast to MHD) a large proportion of this transport arises from the pressure anisotropy directly. Some similar results were found in Reference Sharma, Hammett, Quataert and StoneS06, Sharma et al. (Reference Sharma, Quataert, Hammett and Stone2007) and Foucart et al. (Reference Foucart, Chandra, Gammie, Quataert and Tchekhovskoy2017) using fluid closures. However, these current results have explored only small regions of parameter space (e.g. the case of zero net flux), and it remains unknown how kinetic MRI turbulence relates (if at all) to MHD MRI turbulence. Both the strength of kinetic MRI turbulence and the different heating processes involved (in particular, the relative level of ion versus electron heating; Quataert Reference Quataert1998; Quataert & Gruzinov Reference Quataert and Gruzinov1999), remain crucial unknowns in constraining phenomenological disk models.
Acknowledgements
We would like to thank P. Sharma for kindly providing the modified version of the ZEUS code, which formed the basis for the nonlinear results of § 4.2. J.S. was funded in part by the Gordon and Betty Moore Foundation through grant GBMF5076 to L. Bildsten, E.Q. and E. S. Phinney. E.Q. was supported by Simons Investigator awards from the Simons Foundation and NSF grants AST 13-33612 and AST 17-15054. M.W.K. was supported in part by NASA grant NNX17AK63G and US DOE Contract DE-AC02-09-CH11466. This work used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1548562. Some numerical calculations were carried out on the Comet system at the San Diego supercomputing center, through allocation TG-AST160068.
Appendix A. Linear properties of the KMRI with a background azimuthal–vertical field
In this appendix, we derive various properties of the KMRI in the general case when the background field has a mixed-azimuthal–vertical configuration. We focus on modes with
![]() $k_{x}=k_{y}=0$
as in § 3.1.
$k_{x}=k_{y}=0$
as in § 3.1.
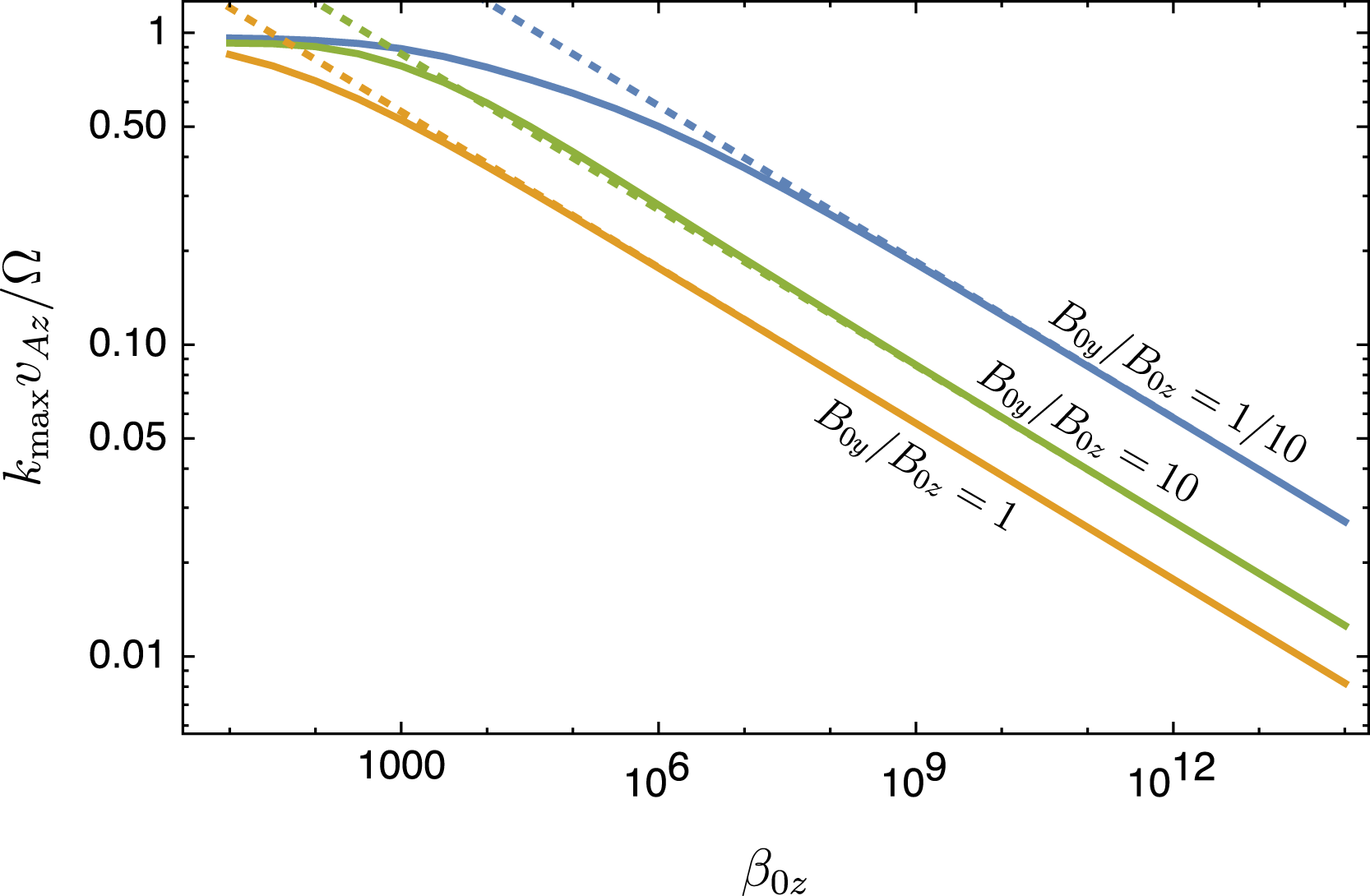
Figure 7. Scaling of
![]() $k_{\text{max}}$
, the wavenumber of the fastest-growing mode, as a function of
$k_{\text{max}}$
, the wavenumber of the fastest-growing mode, as a function of
![]() $\unicode[STIX]{x1D6FD}_{0z}=8\unicode[STIX]{x03C0}p_{0}/B_{0z}^{2}$
for different choices of
$\unicode[STIX]{x1D6FD}_{0z}=8\unicode[STIX]{x03C0}p_{0}/B_{0z}^{2}$
for different choices of
![]() $\unicode[STIX]{x1D6FC}\equiv B_{0y}/B_{0z}$
. Solid lines show results from the numerical solution of the LF dispersion relation; dashed lines show the asymptotic result
$\unicode[STIX]{x1D6FC}\equiv B_{0y}/B_{0z}$
. Solid lines show results from the numerical solution of the LF dispersion relation; dashed lines show the asymptotic result
![]() $k_{\text{max}}v_{A}/\unicode[STIX]{x1D6FA}\sim \unicode[STIX]{x1D6FD}^{-1/6}$
(see (A 2)).
$k_{\text{max}}v_{A}/\unicode[STIX]{x1D6FA}\sim \unicode[STIX]{x1D6FD}^{-1/6}$
(see (A 2)).
A.1 The fastest-growing wavenumber
An important input to the nonlinear arguments put forth in § 3.3 is the scaling of the fastest-growing wavenumber (and growth rate) with
![]() $\unicode[STIX]{x1D6FD}_{0}$
. Our starting point is the Landau-fluid dispersion relation, obtained through the characteristic polynomial of the matrix resulting from the linearization of (2.1)–(2.7) (with
$\unicode[STIX]{x1D6FD}_{0}$
. Our starting point is the Landau-fluid dispersion relation, obtained through the characteristic polynomial of the matrix resulting from the linearization of (2.1)–(2.7) (with
![]() $S/\unicode[STIX]{x1D6FA}=3/2$
and
$S/\unicode[STIX]{x1D6FA}=3/2$
and
![]() $\unicode[STIX]{x1D708}_{c}=0$
). We wish to find
$\unicode[STIX]{x1D708}_{c}=0$
). We wish to find
![]() $k_{\text{max}}$
, the wavenumber that maximizes the growth rate
$k_{\text{max}}$
, the wavenumber that maximizes the growth rate
![]() $\unicode[STIX]{x1D6FE}=\text{Im}(\unicode[STIX]{x1D714})$
, as a function of
$\unicode[STIX]{x1D6FE}=\text{Im}(\unicode[STIX]{x1D714})$
, as a function of
![]() $\unicode[STIX]{x1D6FD}_{0z}=8\unicode[STIX]{x03C0}p_{0}/B_{0z}^{2}$
and
$\unicode[STIX]{x1D6FD}_{0z}=8\unicode[STIX]{x03C0}p_{0}/B_{0z}^{2}$
and
![]() $\unicode[STIX]{x1D6FC}\equiv B_{0y}/B_{0z}$
, assuming
$\unicode[STIX]{x1D6FC}\equiv B_{0y}/B_{0z}$
, assuming
![]() $\unicode[STIX]{x1D6FD}_{0z}\gg 1$
(because we consider only vertical modes, it is most straightforward to work with
$\unicode[STIX]{x1D6FD}_{0z}\gg 1$
(because we consider only vertical modes, it is most straightforward to work with
![]() $\unicode[STIX]{x1D6FD}_{0z}$
and
$\unicode[STIX]{x1D6FD}_{0z}$
and
![]() $v_{Az}$
, as opposed to quantities defined with
$v_{Az}$
, as opposed to quantities defined with
![]() $B_{0}^{2}=B_{0y}^{2}+B_{0z}^{2}$
). Anticipating the scaling
$B_{0}^{2}=B_{0y}^{2}+B_{0z}^{2}$
). Anticipating the scaling
![]() $k_{\text{max}}v_{Az}/\unicode[STIX]{x1D6FA}\sim \unicode[STIX]{x1D6FD}_{0}^{-1/6}$
,
$k_{\text{max}}v_{Az}/\unicode[STIX]{x1D6FA}\sim \unicode[STIX]{x1D6FD}_{0}^{-1/6}$
,
![]() $\unicode[STIX]{x1D714}-\text{i}\sqrt{3}\sim -\unicode[STIX]{x1D6FD}_{0}^{-1/3}$
we insert the ansatz
$\unicode[STIX]{x1D714}-\text{i}\sqrt{3}\sim -\unicode[STIX]{x1D6FD}_{0}^{-1/3}$
we insert the ansatz
![]() $\unicode[STIX]{x1D6FD}_{0z}=\unicode[STIX]{x1D716}^{-6}\bar{\unicode[STIX]{x1D6FD}}_{0z}$
,
$\unicode[STIX]{x1D6FD}_{0z}=\unicode[STIX]{x1D716}^{-6}\bar{\unicode[STIX]{x1D6FD}}_{0z}$
,
![]() $k=\unicode[STIX]{x1D716}k_{0}\bar{\unicode[STIX]{x1D6FD}}_{0z}^{-1/6}$
,
$k=\unicode[STIX]{x1D716}k_{0}\bar{\unicode[STIX]{x1D6FD}}_{0z}^{-1/6}$
,
![]() $\unicode[STIX]{x1D714}=\text{i}\sqrt{3}+\text{i}\unicode[STIX]{x1D716}^{2}\unicode[STIX]{x1D6FE}^{(1)}$
and expand the resulting expression in
$\unicode[STIX]{x1D714}=\text{i}\sqrt{3}+\text{i}\unicode[STIX]{x1D716}^{2}\unicode[STIX]{x1D6FE}^{(1)}$
and expand the resulting expression in
![]() $\unicode[STIX]{x1D716}$
. This yields the solution
$\unicode[STIX]{x1D716}$
. This yields the solution
which is an approximate KMRI dispersion relation, valid at high
![]() $\unicode[STIX]{x1D6FD}$
near the peak growth rate. Maximizing (A 1) over
$\unicode[STIX]{x1D6FD}$
near the peak growth rate. Maximizing (A 1) over
![]() $k_{0}$
, we find,
$k_{0}$
, we find,
and
for the maximum growth rate,
![]() $\unicode[STIX]{x1D6FE}_{\text{max}}=\unicode[STIX]{x1D6FE}(k_{\text{max}})$
.
$\unicode[STIX]{x1D6FE}_{\text{max}}=\unicode[STIX]{x1D6FE}(k_{\text{max}})$
.
Unsurprisingly (given that we carried out an expansion in
![]() $\unicode[STIX]{x1D6FD}_{0}^{-1/6}$
) the expressions (A 2)–(A 3) are accurate only at very high
$\unicode[STIX]{x1D6FD}_{0}^{-1/6}$
) the expressions (A 2)–(A 3) are accurate only at very high
![]() $\unicode[STIX]{x1D6FD}_{0}$
, particularly when
$\unicode[STIX]{x1D6FD}_{0}$
, particularly when
![]() $\unicode[STIX]{x1D6FC}\neq 1$
. A comparison with the true
$\unicode[STIX]{x1D6FC}\neq 1$
. A comparison with the true
![]() $k_{\text{max}}$
, obtained by numerically maximizing the numerically computed dispersion relation, is illustrated in figure 7. We see that, very approximately, the asymptotic result (A 2) is valid when it predicts
$k_{\text{max}}$
, obtained by numerically maximizing the numerically computed dispersion relation, is illustrated in figure 7. We see that, very approximately, the asymptotic result (A 2) is valid when it predicts
![]() $k_{\text{max}}v_{Az}/\unicode[STIX]{x1D6FA}\lesssim 1$
(as should be expected, since
$k_{\text{max}}v_{Az}/\unicode[STIX]{x1D6FA}\lesssim 1$
(as should be expected, since
![]() $k_{\text{max}}v_{Az}/\unicode[STIX]{x1D6FA}\sim 1$
is the fastest-growing wavelength of the standard MRI). This suggests that the results (A 2) and (A 3) are applicable when
$k_{\text{max}}v_{Az}/\unicode[STIX]{x1D6FA}\sim 1$
is the fastest-growing wavelength of the standard MRI). This suggests that the results (A 2) and (A 3) are applicable when
![]() $\unicode[STIX]{x1D6FD}_{0z}\gg (12/\unicode[STIX]{x03C0})\unicode[STIX]{x1D6FC}^{-4}$
for
$\unicode[STIX]{x1D6FD}_{0z}\gg (12/\unicode[STIX]{x03C0})\unicode[STIX]{x1D6FC}^{-4}$
for
![]() $\unicode[STIX]{x1D6FC}\ll 1$
, or when
$\unicode[STIX]{x1D6FC}\ll 1$
, or when
![]() $\unicode[STIX]{x1D6FD}_{0z}\gg (12/\unicode[STIX]{x03C0})\unicode[STIX]{x1D6FC}^{2}$
for
$\unicode[STIX]{x1D6FD}_{0z}\gg (12/\unicode[STIX]{x03C0})\unicode[STIX]{x1D6FC}^{2}$
for
![]() $\unicode[STIX]{x1D6FC}\gg 1$
. For
$\unicode[STIX]{x1D6FC}\gg 1$
. For
![]() $\unicode[STIX]{x1D6FD}_{0z}$
lower than these estimates,
$\unicode[STIX]{x1D6FD}_{0z}$
lower than these estimates,
![]() $k_{\text{max}}$
is less than the prediction (A 2) (there are also minor deviations above the prediction (A 2) when
$k_{\text{max}}$
is less than the prediction (A 2) (there are also minor deviations above the prediction (A 2) when
![]() $\unicode[STIX]{x1D6FC}>1$
, see figure 7). It is also worth noting that the dispersion relation around
$\unicode[STIX]{x1D6FC}>1$
, see figure 7). It is also worth noting that the dispersion relation around
![]() $k\approx k_{\text{max}}$
is not very strongly peaked (see, e.g. figure 1 in the main text). This implies that the fastest-growing mode grows only slightly faster than those with a similar wavelength, and it is unlikely to completely dominate by the time it reaches nonlinear amplitudes (see §§ 3.3 and 4.2).
$k\approx k_{\text{max}}$
is not very strongly peaked (see, e.g. figure 1 in the main text). This implies that the fastest-growing mode grows only slightly faster than those with a similar wavelength, and it is unlikely to completely dominate by the time it reaches nonlinear amplitudes (see §§ 3.3 and 4.2).
A.2 The fastest-growing mode
The structure of the fastest-growing KMRI mode is also relevant to the nonlinear arguments of § 3.3. This can be found by inserting
![]() $k_{\text{max}}$
and
$k_{\text{max}}$
and
![]() $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D6FE}_{\text{max}}$
into the matrix resulting from the linearization of (2.1)–(2.7), and solving for the amplitudes of each component
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D6FE}_{\text{max}}$
into the matrix resulting from the linearization of (2.1)–(2.7), and solving for the amplitudes of each component
![]() $\unicode[STIX]{x1D6FF}u_{x}$
,
$\unicode[STIX]{x1D6FF}u_{x}$
,
![]() $\unicode[STIX]{x1D6FF}B_{x}$
, etc., in terms of
$\unicode[STIX]{x1D6FF}B_{x}$
, etc., in terms of
![]() $\unicode[STIX]{x1D6FF}p_{\bot }$
. To lowest order in
$\unicode[STIX]{x1D6FF}p_{\bot }$
. To lowest order in
![]() $\unicode[STIX]{x1D6FD}_{0z}^{-1}$
, this yields
$\unicode[STIX]{x1D6FD}_{0z}^{-1}$
, this yields
![]() $\unicode[STIX]{x1D6FF}p_{\Vert }\approx -\unicode[STIX]{x1D6FC}^{2}\unicode[STIX]{x1D6FF}p_{\bot }$
, as well as the following relations for the fastest-growing KMRI mode:
$\unicode[STIX]{x1D6FF}p_{\Vert }\approx -\unicode[STIX]{x1D6FC}^{2}\unicode[STIX]{x1D6FF}p_{\bot }$
, as well as the following relations for the fastest-growing KMRI mode:
We see that
![]() $\unicode[STIX]{x1D6FF}B_{x}/B_{0}\sim \unicode[STIX]{x1D6FD}_{0}^{1/3}\unicode[STIX]{x1D6FF}B_{y}/B_{0}$
, viz., the mode is dominated by the radial magnetic field.
$\unicode[STIX]{x1D6FF}B_{x}/B_{0}\sim \unicode[STIX]{x1D6FD}_{0}^{1/3}\unicode[STIX]{x1D6FF}B_{y}/B_{0}$
, viz., the mode is dominated by the radial magnetic field.
A more intuitive way of understanding the structure of the KMRI mode is through the relations
![]() $\unicode[STIX]{x1D6FF}p_{\bot }/p_{0}\approx \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70C}/\unicode[STIX]{x1D70C}_{0}-\text{i}\sqrt{\unicode[STIX]{x03C0}}\unicode[STIX]{x1D709}\unicode[STIX]{x1D6FF}B/B_{0}$
, and
$\unicode[STIX]{x1D6FF}p_{\bot }/p_{0}\approx \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70C}/\unicode[STIX]{x1D70C}_{0}-\text{i}\sqrt{\unicode[STIX]{x03C0}}\unicode[STIX]{x1D709}\unicode[STIX]{x1D6FF}B/B_{0}$
, and
![]() $\unicode[STIX]{x1D6FF}p_{\Vert }/p_{0}\approx \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70C}/\unicode[STIX]{x1D70C}_{0}+\text{i}\sqrt{\unicode[STIX]{x03C0}}\unicode[STIX]{x1D709}\unicode[STIX]{x1D6FF}B/B_{0}$
, where
$\unicode[STIX]{x1D6FF}p_{\Vert }/p_{0}\approx \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70C}/\unicode[STIX]{x1D70C}_{0}+\text{i}\sqrt{\unicode[STIX]{x03C0}}\unicode[STIX]{x1D709}\unicode[STIX]{x1D6FF}B/B_{0}$
, where
![]() $\unicode[STIX]{x1D709}=\unicode[STIX]{x1D714}/(\sqrt{2}\hat{\boldsymbol{b}}\cdot \boldsymbol{k}\,c_{s})$
and
$\unicode[STIX]{x1D709}=\unicode[STIX]{x1D714}/(\sqrt{2}\hat{\boldsymbol{b}}\cdot \boldsymbol{k}\,c_{s})$
and
![]() $\unicode[STIX]{x1D6FF}B/B_{0}=\unicode[STIX]{x1D6FF}B_{y}B_{0y}/B_{0}^{2}$
is the perturbation to the field strength. These relations are straightforwardly derived from the linear
$\unicode[STIX]{x1D6FF}B/B_{0}=\unicode[STIX]{x1D6FF}B_{y}B_{0y}/B_{0}^{2}$
is the perturbation to the field strength. These relations are straightforwardly derived from the linear
![]() $\unicode[STIX]{x1D6FF}p_{\bot }$
and
$\unicode[STIX]{x1D6FF}p_{\bot }$
and
![]() $\unicode[STIX]{x1D6FF}p_{\Vert }$
equations by balancing the production of pressure anisotropy against the smoothing action of the heat fluxes; see Reference Quataert, Dorland and HammettQ02. For
$\unicode[STIX]{x1D6FF}p_{\Vert }$
equations by balancing the production of pressure anisotropy against the smoothing action of the heat fluxes; see Reference Quataert, Dorland and HammettQ02. For
![]() $\unicode[STIX]{x1D6FC}=B_{0y}/B_{0z}\approx 1$
, these lead to (3.6), which is used in §§ 3.3 and 6 to estimate the amplitude at which the KMRI mode reaches the firehose and mirror limits (inserting
$\unicode[STIX]{x1D6FC}=B_{0y}/B_{0z}\approx 1$
, these lead to (3.6), which is used in §§ 3.3 and 6 to estimate the amplitude at which the KMRI mode reaches the firehose and mirror limits (inserting
![]() $k_{\text{max}}$
, one can also obtain (A 5)).
$k_{\text{max}}$
, one can also obtain (A 5)).
Appendix B. The form of the nonlinearity in growing KMRI modes
In this appendix, we derive, using asymptotic expansions, the form of the nonlinearity in growing KMRI modes. The method used is almost identical to that in the appendices of Squire et al. (Reference Squire, Schekochihin and Quataert2017), and the results are very similar, yielding few surprises. However, the results do serve to more formally justify some of the claims made in the main text, in particular those relating to the smoothing effects of the heat fluxes in §§ 2.3 and 3.2. They also allow one to explicitly calculate the form of the nonlinearity that causes the changes to KMRI-mode shape illustrated in figure 2.
We consider three cases – a double-adiabatic model, a collisionless LF model and a Braginskii MHD model – each with a purely vertical field (see §§ 3.2–3.2.2 and figure 2). While the double-adiabatic model is not considered in the main text (neglect of the heat fluxes is never a good approximation at high
![]() $\unicode[STIX]{x1D6FD}$
), it provides a nice illustration of the importance of heat fluxes for high-
$\unicode[STIX]{x1D6FD}$
), it provides a nice illustration of the importance of heat fluxes for high-
![]() $\unicode[STIX]{x1D6FD}$
KMRI dynamics. We treat only the early nonlinear behaviour, that is, when pressure anisotropy first becomes important at low mode amplitudes. We also do not treat the
$\unicode[STIX]{x1D6FD}$
KMRI dynamics. We treat only the early nonlinear behaviour, that is, when pressure anisotropy first becomes important at low mode amplitudes. We also do not treat the
![]() $B_{0y}\neq 0$
KMRI (§ 3.3), since such modes stay close to linear until
$B_{0y}\neq 0$
KMRI (§ 3.3), since such modes stay close to linear until
![]() $\unicode[STIX]{x0394}p$
reaches the firehose and mirror limits, at which point there are strong nonlinear modifications that cannot be captured with this type of asymptotic method (see figure 3).
$\unicode[STIX]{x0394}p$
reaches the firehose and mirror limits, at which point there are strong nonlinear modifications that cannot be captured with this type of asymptotic method (see figure 3).
B.1 Equations and method
Our method here is nearly identical to that used in Squire et al. (Reference Squire, Schekochihin and Quataert2017) to study shear-Alfvén waves, with only minor modifications to the equations to account for the rotation and shear flow. We consider a mode of wavelength
![]() $2\unicode[STIX]{x03C0}/k_{\Vert }$
in a background plasma with density
$2\unicode[STIX]{x03C0}/k_{\Vert }$
in a background plasma with density
![]() $\unicode[STIX]{x1D70C}_{0}$
, thermal pressure
$\unicode[STIX]{x1D70C}_{0}$
, thermal pressure
![]() $p_{0}$
, and vertical magnetic field
$p_{0}$
, and vertical magnetic field
![]() $\boldsymbol{B}_{0}=B_{0}\hat{\boldsymbol{z}}$
. For simplicity, we normalize length scales to
$\boldsymbol{B}_{0}=B_{0}\hat{\boldsymbol{z}}$
. For simplicity, we normalize length scales to
![]() $k_{\Vert }^{-1}$
, velocities to
$k_{\Vert }^{-1}$
, velocities to
![]() $v_{A0}\equiv B_{0}/\sqrt{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}$
, time scales to
$v_{A0}\equiv B_{0}/\sqrt{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}$
, time scales to
![]() $\unicode[STIX]{x1D714}_{A}^{-1}\equiv (k_{\Vert }v_{A0})^{-1}$
, densities to
$\unicode[STIX]{x1D714}_{A}^{-1}\equiv (k_{\Vert }v_{A0})^{-1}$
, densities to
![]() $\unicode[STIX]{x1D70C}_{0}$
, pressures to
$\unicode[STIX]{x1D70C}_{0}$
, pressures to
![]() $p_{0}$
and magnetic fields to
$p_{0}$
and magnetic fields to
![]() $B_{0}$
. Splitting the velocity
$B_{0}$
. Splitting the velocity
![]() $\boldsymbol{u}$
into its equilibrium (
$\boldsymbol{u}$
into its equilibrium (
![]() $\boldsymbol{U}_{0}=-Sx\hat{\boldsymbol{y}}$
) and fluctuating (
$\boldsymbol{U}_{0}=-Sx\hat{\boldsymbol{y}}$
) and fluctuating (
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{u}$
) parts, equations (2.1)–(2.7) become, respectively,
$\unicode[STIX]{x1D6FF}\boldsymbol{u}$
) parts, equations (2.1)–(2.7) become, respectively,
where
![]() $\overline{\unicode[STIX]{x1D708}}_{c}\equiv \unicode[STIX]{x1D708}_{c}/\unicode[STIX]{x1D714}_{A}$
and
$\overline{\unicode[STIX]{x1D708}}_{c}\equiv \unicode[STIX]{x1D708}_{c}/\unicode[STIX]{x1D714}_{A}$
and
![]() $\overline{\unicode[STIX]{x1D6FA}}\equiv \unicode[STIX]{x1D6FA}/\unicode[STIX]{x1D714}_{A}$
. The heat fluxes
$\overline{\unicode[STIX]{x1D6FA}}\equiv \unicode[STIX]{x1D6FA}/\unicode[STIX]{x1D714}_{A}$
. The heat fluxes
![]() $q_{\bot ,\Vert }$
are normalized using the sound speed
$q_{\bot ,\Vert }$
are normalized using the sound speed
![]() $c_{s}\equiv \unicode[STIX]{x1D6FD}_{0}^{1/2}v_{A0}=\sqrt{2p_{0}/\unicode[STIX]{x1D70C}_{0}}$
(note that we have changed the definition of
$c_{s}\equiv \unicode[STIX]{x1D6FD}_{0}^{1/2}v_{A0}=\sqrt{2p_{0}/\unicode[STIX]{x1D70C}_{0}}$
(note that we have changed the definition of
![]() $c_{s}$
from the main text here, so as to remove various inconvenient factors of
$c_{s}$
from the main text here, so as to remove various inconvenient factors of
![]() $2$
from (B 1)–(B 7)). As in the main text,
$2$
from (B 1)–(B 7)). As in the main text,
![]() $\unicode[STIX]{x1D6E5}\equiv p_{\bot }-p_{\Vert }$
denotes the dimensionless pressure anisotropy,
$\unicode[STIX]{x1D6E5}\equiv p_{\bot }-p_{\Vert }$
denotes the dimensionless pressure anisotropy,
![]() $\unicode[STIX]{x1D6FD}_{0}\equiv 8\unicode[STIX]{x03C0}p_{0}/B_{0}^{2}$
, and
$\unicode[STIX]{x1D6FD}_{0}\equiv 8\unicode[STIX]{x03C0}p_{0}/B_{0}^{2}$
, and
is the convective derivative.
Following § 3.2, we focus on the nonlinear evolution of a 1-D (in
![]() $z$
) channel mode. This involves an asymptotic expansion of (B 1)–(B 7), which is constructed as follows. Figure 1 shows that the
$z$
) channel mode. This involves an asymptotic expansion of (B 1)–(B 7), which is constructed as follows. Figure 1 shows that the
![]() $k_{\Vert }=k_{z}$
KMRI mode grows fastest for
$k_{\Vert }=k_{z}$
KMRI mode grows fastest for
![]() $k_{\Vert }v_{A}/\unicode[STIX]{x1D6FA}\sim 1$
, and so we order
$k_{\Vert }v_{A}/\unicode[STIX]{x1D6FA}\sim 1$
, and so we order
![]() $\overline{\unicode[STIX]{x1D6FA}}\sim 1$
. Following Squire et al. (Reference Squire, Schekochihin and Quataert2017), we order the (dimensionless) MRI-mode amplitude
$\overline{\unicode[STIX]{x1D6FA}}\sim 1$
. Following Squire et al. (Reference Squire, Schekochihin and Quataert2017), we order the (dimensionless) MRI-mode amplitude
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{B}_{\bot }\sim \unicode[STIX]{x1D6FF}\boldsymbol{u}_{\bot }\sim \unicode[STIX]{x1D716}\ll 1$
and the equilibrium plasma beta parameter
$\unicode[STIX]{x1D6FF}\boldsymbol{B}_{\bot }\sim \unicode[STIX]{x1D6FF}\boldsymbol{u}_{\bot }\sim \unicode[STIX]{x1D716}\ll 1$
and the equilibrium plasma beta parameter
![]() $\unicode[STIX]{x1D6FD}_{0}$
such that the effect of the pressure anisotropy
$\unicode[STIX]{x1D6FD}_{0}$
such that the effect of the pressure anisotropy
![]() $\unicode[STIX]{x1D6E5}$
is as important as that of the linear terms, viz.,
$\unicode[STIX]{x1D6E5}$
is as important as that of the linear terms, viz.,
![]() $\unicode[STIX]{x1D6FD}_{0}\unicode[STIX]{x1D6E5}\sim 1$
. Because the growth rate of the fastest-growing MRI mode is
$\unicode[STIX]{x1D6FD}_{0}\unicode[STIX]{x1D6E5}\sim 1$
. Because the growth rate of the fastest-growing MRI mode is
![]() $\unicode[STIX]{x1D6FE}\sim \unicode[STIX]{x1D6FA}\sim \unicode[STIX]{x1D714}_{A}$
, we order the (dimensionless) spatial and temporal derivatives to be
$\unicode[STIX]{x1D6FE}\sim \unicode[STIX]{x1D6FA}\sim \unicode[STIX]{x1D714}_{A}$
, we order the (dimensionless) spatial and temporal derivatives to be
![]() ${\sim}O(1)$
. This ordering captures nonlinear effects on the MRI mode just before it drives the pressure anisotropy to the mirror limit
${\sim}O(1)$
. This ordering captures nonlinear effects on the MRI mode just before it drives the pressure anisotropy to the mirror limit
![]() $\unicode[STIX]{x1D6FD}_{0}\unicode[STIX]{x1D6E5}\approx 1$
, in both the collisionless and weakly collisional (Braginskii) cases.
$\unicode[STIX]{x1D6FD}_{0}\unicode[STIX]{x1D6E5}\approx 1$
, in both the collisionless and weakly collisional (Braginskii) cases.
In what follows, we use
![]() $\langle f\rangle$
to denote a spatial (
$\langle f\rangle$
to denote a spatial (
![]() $z$
) average of some function
$z$
) average of some function
![]() $f$
and
$f$
and
![]() $\widetilde{f}\equiv f-\langle f\rangle$
to denote the spatially varying part of
$\widetilde{f}\equiv f-\langle f\rangle$
to denote the spatially varying part of
![]() $f$
.
$f$
.
B.2 Collisionless limit: double-adiabatic closure
Because the pressure anisotropy is generated proportional to the change in
![]() $B$
, in the double-adiabatic case
$B$
, in the double-adiabatic case
![]() $\unicode[STIX]{x1D6E5}$
scales as
$\unicode[STIX]{x1D6E5}$
scales as
![]() ${\sim}\unicode[STIX]{x1D6FF}B_{\bot }^{2}$
. Thus we order
${\sim}\unicode[STIX]{x1D6FF}B_{\bot }^{2}$
. Thus we order
![]() $\unicode[STIX]{x1D6FD}_{0}\sim \unicode[STIX]{x1D716}^{-2}$
. The ordering of all variables is then as follows (cf. Squire et al.
Reference Squire, Schekochihin and Quataert2017):
$\unicode[STIX]{x1D6FD}_{0}\sim \unicode[STIX]{x1D716}^{-2}$
. The ordering of all variables is then as follows (cf. Squire et al.
Reference Squire, Schekochihin and Quataert2017):
Order
![]() $\unicode[STIX]{x1D716}^{0}$
. Only the
$\unicode[STIX]{x1D716}^{0}$
. Only the
![]() $z$
component of (B 2) contributes at this order, giving
$z$
component of (B 2) contributes at this order, giving
![]() $\unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D6FF}p_{\Vert 2}=0$
or
$\unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D6FF}p_{\Vert 2}=0$
or
![]() $\widetilde{\unicode[STIX]{x1D6FF}p_{\Vert 2}}=0$
. This condition expresses parallel pressure balance.
$\widetilde{\unicode[STIX]{x1D6FF}p_{\Vert 2}}=0$
. This condition expresses parallel pressure balance.
Order
![]() $\unicode[STIX]{x1D716}^{1}$
. The parallel component of the momentum equation (B 2) gives
$\unicode[STIX]{x1D716}^{1}$
. The parallel component of the momentum equation (B 2) gives
![]() $\widetilde{\unicode[STIX]{x1D6FF}p_{\Vert 3}}=0$
. The perpendicular components of the momentum and induction equations (B 2)–(B 3) provide evolution equations for the linear MRI:
$\widetilde{\unicode[STIX]{x1D6FF}p_{\Vert 3}}=0$
. The perpendicular components of the momentum and induction equations (B 2)–(B 3) provide evolution equations for the linear MRI:
To close this system, we require
![]() $\unicode[STIX]{x1D6E5}_{2}=\unicode[STIX]{x1D6FF}p_{\bot 2}-\unicode[STIX]{x1D6FF}p_{\Vert 2}$
as a function of
$\unicode[STIX]{x1D6E5}_{2}=\unicode[STIX]{x1D6FF}p_{\bot 2}-\unicode[STIX]{x1D6FF}p_{\Vert 2}$
as a function of
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{u}_{\bot 2}$
and
$\unicode[STIX]{x1D6FF}\boldsymbol{u}_{\bot 2}$
and
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{B}_{\bot 2}$
, which is obtained at next order.
$\unicode[STIX]{x1D6FF}\boldsymbol{B}_{\bot 2}$
, which is obtained at next order.
Order
![]() $\unicode[STIX]{x1D716}^{2}$
. At this order, we require only the pressure equations (B 4)–(B 5) to obtain
$\unicode[STIX]{x1D716}^{2}$
. At this order, we require only the pressure equations (B 4)–(B 5) to obtain
![]() $\unicode[STIX]{x1D6E5}_{2}$
for use in (B 10). Expanding
$\unicode[STIX]{x1D6E5}_{2}$
for use in (B 10). Expanding
![]() $\hat{\boldsymbol{b}}\hat{\boldsymbol{b}}\,\boldsymbol{ : }\,\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FF}\boldsymbol{u}=\hat{b}_{z}^{2}\unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D6FF}u_{z}+\hat{\boldsymbol{b}}\hat{\boldsymbol{b}}\,\boldsymbol{ : }\,\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FF}\boldsymbol{u}_{\bot }$
, equations (B 4)–(B 5) become
$\hat{\boldsymbol{b}}\hat{\boldsymbol{b}}\,\boldsymbol{ : }\,\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FF}\boldsymbol{u}=\hat{b}_{z}^{2}\unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D6FF}u_{z}+\hat{\boldsymbol{b}}\hat{\boldsymbol{b}}\,\boldsymbol{ : }\,\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FF}\boldsymbol{u}_{\bot }$
, equations (B 4)–(B 5) become
where
![]() $\unicode[STIX]{x1D6FF}B_{\bot 1}^{2}\equiv \unicode[STIX]{x1D6FF}B_{x1}^{2}+\unicode[STIX]{x1D6FF}B_{y1}^{2}$
; the final equalities in these equations follow from (B 11). We can then solve for
$\unicode[STIX]{x1D6FF}B_{\bot 1}^{2}\equiv \unicode[STIX]{x1D6FF}B_{x1}^{2}+\unicode[STIX]{x1D6FF}B_{y1}^{2}$
; the final equalities in these equations follow from (B 11). We can then solve for
![]() $\unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D6FF}u_{z2}=\widetilde{\unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D6FF}u_{z2}}$
using (B 13) and insert this into (B 12) to find
$\unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D6FF}u_{z2}=\widetilde{\unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D6FF}u_{z2}}$
using (B 13) and insert this into (B 12) to find
If we then assume that the mode starts growing from vanishingly small initial conditions, equation (B 14) may be straightforwardly integrated to obtain
This expression may be inserted into (B 10) to yield a simple nonlinear equation for the growing MRI mode:
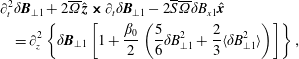 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x2202}_{t}^{2}\unicode[STIX]{x1D6FF}\boldsymbol{B}_{\bot 1}+2\overline{\unicode[STIX]{x1D6FA}}\hat{\boldsymbol{z}}\boldsymbol{\times }\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D6FF}\boldsymbol{B}_{\bot 1}-2\overline{S}\overline{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D6FF}B_{x1}\hat{\boldsymbol{x}}\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x2202}_{z}^{2}\left\{\unicode[STIX]{x1D6FF}\boldsymbol{B}_{\bot 1}\left[1+\frac{\unicode[STIX]{x1D6FD}_{0}}{2}\left(\frac{5}{6}\unicode[STIX]{x1D6FF}B_{\bot 1}^{2}+\frac{2}{3}\langle \unicode[STIX]{x1D6FF}B_{\bot 1}^{2}\rangle \right)\right]\right\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x2202}_{t}^{2}\unicode[STIX]{x1D6FF}\boldsymbol{B}_{\bot 1}+2\overline{\unicode[STIX]{x1D6FA}}\hat{\boldsymbol{z}}\boldsymbol{\times }\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D6FF}\boldsymbol{B}_{\bot 1}-2\overline{S}\overline{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D6FF}B_{x1}\hat{\boldsymbol{x}}\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x2202}_{z}^{2}\left\{\unicode[STIX]{x1D6FF}\boldsymbol{B}_{\bot 1}\left[1+\frac{\unicode[STIX]{x1D6FD}_{0}}{2}\left(\frac{5}{6}\unicode[STIX]{x1D6FF}B_{\bot 1}^{2}+\frac{2}{3}\langle \unicode[STIX]{x1D6FF}B_{\bot 1}^{2}\rangle \right)\right]\right\},\end{eqnarray}$$
where we have grouped all nonlinear terms on the right-hand side.
This rather simple expression of
![]() $\unicode[STIX]{x1D6E5}_{2}$
(B 15) arises because, while parallel pressure balance enforces
$\unicode[STIX]{x1D6E5}_{2}$
(B 15) arises because, while parallel pressure balance enforces
![]() $\unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D6FF}p_{\Vert }\approx 0$
in the growing mode, there is no equivalent pressure balance condition for
$\unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D6FF}p_{\Vert }\approx 0$
in the growing mode, there is no equivalent pressure balance condition for
![]() $\unicode[STIX]{x1D6FF}p_{\bot }$
. The same result can also be obtained by projecting the driving of
$\unicode[STIX]{x1D6FF}p_{\bot }$
. The same result can also be obtained by projecting the driving of
![]() $\unicode[STIX]{x0394}p$
due to the MRI mode onto the eigenmodes of the double-adiabatic equations; this agrees with 1-D nonlinear simulations (not shown). Because the spatial variation in the anisotropy is comparable to its mean (i.e.
$\unicode[STIX]{x0394}p$
due to the MRI mode onto the eigenmodes of the double-adiabatic equations; this agrees with 1-D nonlinear simulations (not shown). Because the spatial variation in the anisotropy is comparable to its mean (i.e.
![]() $\langle \unicode[STIX]{x1D6E5}_{2}\rangle \sim \widetilde{\unicode[STIX]{x1D6E5}_{2}}$
) the double-adiabatic model will cause nonlinear modifications to the mode shape as it approaches the mirror limit (similar to the Braginskii model; see figure 2(c) and § B.4).
$\langle \unicode[STIX]{x1D6E5}_{2}\rangle \sim \widetilde{\unicode[STIX]{x1D6E5}_{2}}$
) the double-adiabatic model will cause nonlinear modifications to the mode shape as it approaches the mirror limit (similar to the Braginskii model; see figure 2(c) and § B.4).
B.3 Collisionless: Landau-fluid closure
In this section, we repeat the calculation detailed in § B.2 but include the heat fluxes
![]() $q_{\bot }$
(B 6) and
$q_{\bot }$
(B 6) and
![]() $q_{\Vert }$
(B 7) with
$q_{\Vert }$
(B 7) with
![]() $\overline{\unicode[STIX]{x1D708}}_{c}=0$
. In a high-
$\overline{\unicode[STIX]{x1D708}}_{c}=0$
. In a high-
![]() $\unicode[STIX]{x1D6FD}$
plasma with Alfvénic fluctuations, such flows rapidly smooth pressure perturbations and, as a result, lead to a
$\unicode[STIX]{x1D6FD}$
plasma with Alfvénic fluctuations, such flows rapidly smooth pressure perturbations and, as a result, lead to a
![]() $\unicode[STIX]{x1D6E5}_{2}$
that is smooth, viz.,
$\unicode[STIX]{x1D6E5}_{2}$
that is smooth, viz.,
![]() $\widetilde{\unicode[STIX]{x1D6E5}_{2}}=0$
. The ordering is the same as that used in the double-adiabatic case (§ B.2), but with the addition of the heat fluxes,
$\widetilde{\unicode[STIX]{x1D6E5}_{2}}=0$
. The ordering is the same as that used in the double-adiabatic case (§ B.2), but with the addition of the heat fluxes,
The
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }(q_{\bot ,\Vert }\hat{\boldsymbol{b}})$
contributions to the pressure equations (B 4)–(B 5) then simplify to
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }(q_{\bot ,\Vert }\hat{\boldsymbol{b}})$
contributions to the pressure equations (B 4)–(B 5) then simplify to
![]() $\unicode[STIX]{x1D716}^{2}\unicode[STIX]{x2202}_{z}q_{\bot ,\Vert 2}+\unicode[STIX]{x1D716}^{3}\unicode[STIX]{x2202}_{z}q_{\bot ,\Vert 3}+O(\unicode[STIX]{x1D716}^{4})$
, i.e. heat flows along
$\unicode[STIX]{x1D716}^{2}\unicode[STIX]{x2202}_{z}q_{\bot ,\Vert 2}+\unicode[STIX]{x1D716}^{3}\unicode[STIX]{x2202}_{z}q_{\bot ,\Vert 3}+O(\unicode[STIX]{x1D716}^{4})$
, i.e. heat flows along
![]() $\boldsymbol{B}_{0}=\hat{\boldsymbol{z}}$
to lowest order.
$\boldsymbol{B}_{0}=\hat{\boldsymbol{z}}$
to lowest order.
The equations up to order
![]() $\unicode[STIX]{x1D716}^{1}$
are identical to those found in § B.2, aside from additional contributions from the
$\unicode[STIX]{x1D716}^{1}$
are identical to those found in § B.2, aside from additional contributions from the
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }(q_{\bot ,\Vert }\hat{\boldsymbol{b}})$
terms in the pressure equations (B 4)–(B 5), namely,
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }(q_{\bot ,\Vert }\hat{\boldsymbol{b}})$
terms in the pressure equations (B 4)–(B 5), namely,
where we have used
![]() $\unicode[STIX]{x2202}_{z}^{2}/|k_{z}|=-|k_{z}|$
to simplify the non-local diffusion operators. Combining (B 19)–(B 20) with the continuity equation (B 1) and parallel pressure balance
$\unicode[STIX]{x2202}_{z}^{2}/|k_{z}|=-|k_{z}|$
to simplify the non-local diffusion operators. Combining (B 19)–(B 20) with the continuity equation (B 1) and parallel pressure balance
![]() $\unicode[STIX]{x1D6FF}\widetilde{p_{\Vert 2}}=0$
, we obtain
$\unicode[STIX]{x1D6FF}\widetilde{p_{\Vert 2}}=0$
, we obtain
This formally justifies the statements in §§ 3.2 and 2.3 that
![]() $\unicode[STIX]{x1D6E5}$
is spatially constant to lowest order.
$\unicode[STIX]{x1D6E5}$
is spatially constant to lowest order.
At order
![]() $\unicode[STIX]{x1D716}^{2}$
, the pressure equations (B 4)–(B 5) are
$\unicode[STIX]{x1D716}^{2}$
, the pressure equations (B 4)–(B 5) are
Spatially averaging these equations, using
![]() $\widetilde{\unicode[STIX]{x1D6FF}p_{\bot 2}}=\widetilde{\unicode[STIX]{x1D6FF}p_{\Vert 2}}=0$
, and again assuming that the mode growth starts from negligibly small amplitudes (i.e.
$\widetilde{\unicode[STIX]{x1D6FF}p_{\bot 2}}=\widetilde{\unicode[STIX]{x1D6FF}p_{\Vert 2}}=0$
, and again assuming that the mode growth starts from negligibly small amplitudes (i.e.
![]() $\unicode[STIX]{x1D6FF}B_{\bot 1}^{2}(t=0)=0$
), we find
$\unicode[STIX]{x1D6FF}B_{\bot 1}^{2}(t=0)=0$
), we find
This can be inserted into (B 10)–(B 11) to obtain the following evolution equation for
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{B}_{\bot 1}$
:
$\unicode[STIX]{x1D6FF}\boldsymbol{B}_{\bot 1}$
:
which remains valid until
![]() $\unicode[STIX]{x1D6E5}_{2}$
exceeds the mirror threshold (at which point its growth should be limited by the unresolved mirror instability, as discussed in § 3.2).
$\unicode[STIX]{x1D6E5}_{2}$
exceeds the mirror threshold (at which point its growth should be limited by the unresolved mirror instability, as discussed in § 3.2).
As expected, the presence of such strong heat fluxes has rendered the KMRI equations (B 10)–(B 11) much simpler than in the double-adiabatic case.Footnote
13
Physically, the spatial average inside the nonlinear term in (B 25) implies that, if a KMRI mode is initially sinusoidal, it will remain so even as it becomes nonlinear (see figure 2
b for a demonstration of this property). We can then use (B 25) to write down an ordinary differential equation for the amplitude evolution of a single MRI mode
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{B}_{\bot }=\unicode[STIX]{x1D6FF}\boldsymbol{B}_{\bot }(t)\text{e}^{\text{i}k_{\Vert }z}$
,
$\unicode[STIX]{x1D6FF}\boldsymbol{B}_{\bot }=\unicode[STIX]{x1D6FF}\boldsymbol{B}_{\bot }(t)\text{e}^{\text{i}k_{\Vert }z}$
,
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{u}_{\bot }=\unicode[STIX]{x1D6FF}\boldsymbol{u}_{\bot }(t)\text{e}^{\text{i}k_{\Vert }z}$
:
$\unicode[STIX]{x1D6FF}\boldsymbol{u}_{\bot }=\unicode[STIX]{x1D6FF}\boldsymbol{u}_{\bot }(t)\text{e}^{\text{i}k_{\Vert }z}$
:
where we have used
![]() $\langle \sin ^{2}(k_{\Vert }z)\rangle =1/2$
. Solutions to (B 26)–(B 27) correctly reproduce the change in relative amplitudes of
$\langle \sin ^{2}(k_{\Vert }z)\rangle =1/2$
. Solutions to (B 26)–(B 27) correctly reproduce the change in relative amplitudes of
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{B}_{\bot }$
and
$\unicode[STIX]{x1D6FF}\boldsymbol{B}_{\bot }$
and
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{u}_{\bot }$
as seen in figure 2(b) (e.g. the relative increase in
$\unicode[STIX]{x1D6FF}\boldsymbol{u}_{\bot }$
as seen in figure 2(b) (e.g. the relative increase in
![]() $\unicode[STIX]{x1D6FF}u_{y}$
and relative decrease of
$\unicode[STIX]{x1D6FF}u_{y}$
and relative decrease of
![]() $\unicode[STIX]{x1D6FF}u_{x}$
). Of course, if there is more than one growing mode, the pressure-anisotropy nonlinearity (B 24) does couple the modes, which could allow, for example, a larger-wavelength mode to ‘take over’ due to the positive pressure anisotropy (see § 3.2).
$\unicode[STIX]{x1D6FF}u_{x}$
). Of course, if there is more than one growing mode, the pressure-anisotropy nonlinearity (B 24) does couple the modes, which could allow, for example, a larger-wavelength mode to ‘take over’ due to the positive pressure anisotropy (see § 3.2).
If one were so inclined, a continuation of the expansion to
![]() $O(\unicode[STIX]{x1D716}^{3})$
would yield equations for the spatial variation in
$O(\unicode[STIX]{x1D716}^{3})$
would yield equations for the spatial variation in
![]() $\unicode[STIX]{x1D6E5}$
. However, because the expected effect on the mode is very small for
$\unicode[STIX]{x1D6E5}$
. However, because the expected effect on the mode is very small for
![]() $\unicode[STIX]{x1D6FD}_{0}\gg 1$
, we do not do this here (see, e.g. appendix A.3.1 of Squire et al.
Reference Squire, Schekochihin and Quataert2017).
$\unicode[STIX]{x1D6FD}_{0}\gg 1$
, we do not do this here (see, e.g. appendix A.3.1 of Squire et al.
Reference Squire, Schekochihin and Quataert2017).
B.4 Weakly collisional: Braginskii closure
In this section, we treat the weakly collisional, Braginskii MHD limit. As discussed in §§ 2 and 3.2.2, 3.3.2, the Braginskii regime is relevant when
![]() $\overline{\unicode[STIX]{x1D708}}_{c}\equiv \unicode[STIX]{x1D708}_{c}/\unicode[STIX]{x1D714}_{A}\sim \unicode[STIX]{x1D708}_{c}/\unicode[STIX]{x1D6FA}\gg 1$
, with the corrections to the MRI due to pressure anisotropy becoming unimportant when
$\overline{\unicode[STIX]{x1D708}}_{c}\equiv \unicode[STIX]{x1D708}_{c}/\unicode[STIX]{x1D714}_{A}\sim \unicode[STIX]{x1D708}_{c}/\unicode[STIX]{x1D6FA}\gg 1$
, with the corrections to the MRI due to pressure anisotropy becoming unimportant when
![]() $\overline{\unicode[STIX]{x1D708}}_{c}\gtrsim \unicode[STIX]{x1D6FD}$
(see Sharma et al.
Reference Sharma, Hammett and Quataert2003). Within the relevant range
$\overline{\unicode[STIX]{x1D708}}_{c}\gtrsim \unicode[STIX]{x1D6FD}$
(see Sharma et al.
Reference Sharma, Hammett and Quataert2003). Within the relevant range
![]() $1\ll \overline{\unicode[STIX]{x1D708}}_{c}\ll \unicode[STIX]{x1D6FD}$
, one may obtain a variety of behaviours depending upon whether or not the heat fluxes play a significant role in the evolution of
$1\ll \overline{\unicode[STIX]{x1D708}}_{c}\ll \unicode[STIX]{x1D6FD}$
, one may obtain a variety of behaviours depending upon whether or not the heat fluxes play a significant role in the evolution of
![]() $\unicode[STIX]{x0394}p$
. If
$\unicode[STIX]{x0394}p$
. If
![]() $\overline{\unicode[STIX]{x1D708}}_{c}\gg \unicode[STIX]{x1D6FD}^{1/2}$
, the heat fluxes are suppressed by the collisionality and do not strongly influence
$\overline{\unicode[STIX]{x1D708}}_{c}\gg \unicode[STIX]{x1D6FD}^{1/2}$
, the heat fluxes are suppressed by the collisionality and do not strongly influence
![]() $\unicode[STIX]{x0394}p$
; if instead
$\unicode[STIX]{x0394}p$
; if instead
![]() $\overline{\unicode[STIX]{x1D708}}_{c}\lesssim \unicode[STIX]{x1D6FD}^{1/2}$
, the heat fluxes smooth
$\overline{\unicode[STIX]{x1D708}}_{c}\lesssim \unicode[STIX]{x1D6FD}^{1/2}$
, the heat fluxes smooth
![]() $\unicode[STIX]{x0394}p$
in spaceFootnote
14
on a time scale shorter than that over which
$\unicode[STIX]{x0394}p$
in spaceFootnote
14
on a time scale shorter than that over which
![]() $\unicode[STIX]{x0394}p$
is produced by the changing
$\unicode[STIX]{x0394}p$
is produced by the changing
![]() $B$
(see Squire et al.
Reference Squire, Schekochihin and Quataert2017 for further discussion). We present here only the former limit (
$B$
(see Squire et al.
Reference Squire, Schekochihin and Quataert2017 for further discussion). We present here only the former limit (
![]() $\overline{\unicode[STIX]{x1D708}}_{c}\gg \unicode[STIX]{x1D6FD}^{1/2}$
), which leads to the closure used in the main text, equation (2.8); in the
$\overline{\unicode[STIX]{x1D708}}_{c}\gg \unicode[STIX]{x1D6FD}^{1/2}$
), which leads to the closure used in the main text, equation (2.8); in the
![]() $\overline{\unicode[STIX]{x1D708}}_{c}\ll \unicode[STIX]{x1D6FD}^{1/2}$
limit, the heat fluxes smooth out
$\overline{\unicode[STIX]{x1D708}}_{c}\ll \unicode[STIX]{x1D6FD}^{1/2}$
limit, the heat fluxes smooth out
![]() $\unicode[STIX]{x0394}p$
near the nodes of
$\unicode[STIX]{x0394}p$
near the nodes of
![]() $\unicode[STIX]{x1D6FF}B$
and so
$\unicode[STIX]{x1D6FF}B$
and so
![]() $\unicode[STIX]{x0394}p$
is almost spatially constant as the mirror limit is approach (see the discussion in § 3.2.2). In the intermediate case
$\unicode[STIX]{x0394}p$
is almost spatially constant as the mirror limit is approach (see the discussion in § 3.2.2). In the intermediate case
![]() $\overline{\unicode[STIX]{x1D708}}_{c}\sim \unicode[STIX]{x1D6FD}^{1/2}$
, a valid closure for
$\overline{\unicode[STIX]{x1D708}}_{c}\sim \unicode[STIX]{x1D6FD}^{1/2}$
, a valid closure for
![]() $\unicode[STIX]{x0394}p$
has been obtained by Squire et al. (Reference Squire, Schekochihin and Quataert2017) – see their equations (B12)–(B15).
$\unicode[STIX]{x0394}p$
has been obtained by Squire et al. (Reference Squire, Schekochihin and Quataert2017) – see their equations (B12)–(B15).
The ordering introduced above,
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{B}_{\bot }\sim \unicode[STIX]{x1D6FF}\boldsymbol{u}_{\bot }\sim \unicode[STIX]{x1D716}$
with
$\unicode[STIX]{x1D6FF}\boldsymbol{B}_{\bot }\sim \unicode[STIX]{x1D6FF}\boldsymbol{u}_{\bot }\sim \unicode[STIX]{x1D716}$
with
![]() $\unicode[STIX]{x1D6FD}_{0}\unicode[STIX]{x1D6E5}\sim 1$
, coupled with the Braginskii pressure anisotropy
$\unicode[STIX]{x1D6FD}_{0}\unicode[STIX]{x1D6E5}\sim 1$
, coupled with the Braginskii pressure anisotropy
![]() $\unicode[STIX]{x1D6E5}\sim \overline{\unicode[STIX]{x1D708}}_{c}^{-1}\text{d}\ln B/\text{d}t$
, suggests that we order
$\unicode[STIX]{x1D6E5}\sim \overline{\unicode[STIX]{x1D708}}_{c}^{-1}\text{d}\ln B/\text{d}t$
, suggests that we order
![]() $\overline{\unicode[STIX]{x1D708}}_{c}\sim \unicode[STIX]{x1D716}^{2}\unicode[STIX]{x1D6FD}_{0}$
. The simultaneous requirement that
$\overline{\unicode[STIX]{x1D708}}_{c}\sim \unicode[STIX]{x1D716}^{2}\unicode[STIX]{x1D6FD}_{0}$
. The simultaneous requirement that
![]() $\overline{\unicode[STIX]{x1D708}}_{c}\gg \unicode[STIX]{x1D6FD}_{0}^{1/2}$
for the ‘high-collisionality’ regime where heat fluxes are collisionally suppressed then implies the ordering
$\overline{\unicode[STIX]{x1D708}}_{c}\gg \unicode[STIX]{x1D6FD}_{0}^{1/2}$
for the ‘high-collisionality’ regime where heat fluxes are collisionally suppressed then implies the ordering
![]() $\overline{\unicode[STIX]{x1D708}}_{c}\sim O(\unicode[STIX]{x1D716}^{-4})$
,
$\overline{\unicode[STIX]{x1D708}}_{c}\sim O(\unicode[STIX]{x1D716}^{-4})$
,
![]() $\unicode[STIX]{x1D6FD}_{0}\sim O(\unicode[STIX]{x1D716}^{-6})$
. For the other variables, we adopt the orderings
$\unicode[STIX]{x1D6FD}_{0}\sim O(\unicode[STIX]{x1D716}^{-6})$
. For the other variables, we adopt the orderings
![]() $p_{\bot }\sim p_{\Vert }\sim \unicode[STIX]{x1D70C}\sim 1+O(\unicode[STIX]{x1D716}^{6})$
and
$p_{\bot }\sim p_{\Vert }\sim \unicode[STIX]{x1D70C}\sim 1+O(\unicode[STIX]{x1D716}^{6})$
and
![]() $\unicode[STIX]{x1D6FF}u_{z}\sim O(\unicode[STIX]{x1D716}^{6})$
. The
$\unicode[STIX]{x1D6FF}u_{z}\sim O(\unicode[STIX]{x1D716}^{6})$
. The
![]() $O(1)$
and
$O(1)$
and
![]() $O(\unicode[STIX]{x1D716})$
equations are then almost the same as in § B.2: the parallel momentum equation gives
$O(\unicode[STIX]{x1D716})$
equations are then almost the same as in § B.2: the parallel momentum equation gives
![]() $\unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D6FF}p_{\Vert 6}=0$
, and the perpendicular momentum and induction equations are identical to (B 10)–(B 11) but with
$\unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D6FF}p_{\Vert 6}=0$
, and the perpendicular momentum and induction equations are identical to (B 10)–(B 11) but with
![]() $\unicode[STIX]{x1D6E5}_{2}$
replaced by
$\unicode[STIX]{x1D6E5}_{2}$
replaced by
![]() $\unicode[STIX]{x1D6E5}_{6}$
. At
$\unicode[STIX]{x1D6E5}_{6}$
. At
![]() $O(\unicode[STIX]{x1D716}^{2})$
, the pressure equations (B 4) and (B 5) may be combined to give
$O(\unicode[STIX]{x1D716}^{2})$
, the pressure equations (B 4) and (B 5) may be combined to give
the heat-flux terms appear at
![]() $O(\unicode[STIX]{x1D716}^{4})$
. This is exactly as was anticipated (cf. (2.8)). The nonlinear equation for the growing mode is then simply
$O(\unicode[STIX]{x1D716}^{4})$
. This is exactly as was anticipated (cf. (2.8)). The nonlinear equation for the growing mode is then simply
Because the nonlinearity in (B 29) depends on
![]() $\unicode[STIX]{x1D6FF}B_{\bot 1}^{2}(z)$
(rather than
$\unicode[STIX]{x1D6FF}B_{\bot 1}^{2}(z)$
(rather than
![]() $\langle \unicode[STIX]{x1D6FF}B_{\bot 1}^{2}\rangle$
), it will distort the shape of an initially sinusoidal mode, as discussed in § 3.2.2 and exhibited in figure 2(c). Thus, we cannot reduce (B 29) to an ordinary differential equation for a single mode, as in the collisionless (LF) derivation (see (B 26)).
$\langle \unicode[STIX]{x1D6FF}B_{\bot 1}^{2}\rangle$
), it will distort the shape of an initially sinusoidal mode, as discussed in § 3.2.2 and exhibited in figure 2(c). Thus, we cannot reduce (B 29) to an ordinary differential equation for a single mode, as in the collisionless (LF) derivation (see (B 26)).









