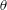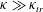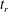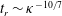1 Introduction
The dynamics of thin planar liquid films on solid surfaces has been extensively studied in the context of free-surface instabilities (Oron, Davis & Bankoff Reference Oron, Davis and Bankoff1997; Craster and Matar Reference Craster and Matar2009). The stability of such films depends on the interplay between surface tension on the one hand, that always stabilizes the film, and intermolecular forces on the other hand, that may destabilize it. The evolution of unstable planar films starts from minute corrugations on the free interface originating from stochastic thermal motion of molecules. In the absence of destabilizing intermolecular forces, the film is stable and dynamically perturbed by corrugations of amplitude
![]() ${\sim}\sqrt{k_{B}T/\unicode[STIX]{x1D6FE}}$
, with
${\sim}\sqrt{k_{B}T/\unicode[STIX]{x1D6FE}}$
, with
![]() $k_{B}$
the Boltzmann constant,
$k_{B}$
the Boltzmann constant,
![]() $T$
the absolute temperature and
$T$
the absolute temperature and
![]() $\unicode[STIX]{x1D6FE}$
the interfacial tension (Aarts, Schmidt & Lekkerkerker Reference Aarts, Schmidt and Lekkerkerker2004). For unstable films, these corrugations spontaneously grow until the film ruptures. In the last decade, thermal fluctuations have been explicitly incorporated into the thin film equation using a stochastic term, bringing simulations (Grün, Mecke & Rauscher Reference Grün, Mecke and Rauscher2006) closer to experiments for planar films (Becker et al.
Reference Becker, Grün, Seemann, Mantz, Jacobs, Mecke and Blossey2003).
$\unicode[STIX]{x1D6FE}$
the interfacial tension (Aarts, Schmidt & Lekkerkerker Reference Aarts, Schmidt and Lekkerkerker2004). For unstable films, these corrugations spontaneously grow until the film ruptures. In the last decade, thermal fluctuations have been explicitly incorporated into the thin film equation using a stochastic term, bringing simulations (Grün, Mecke & Rauscher Reference Grün, Mecke and Rauscher2006) closer to experiments for planar films (Becker et al.
Reference Becker, Grün, Seemann, Mantz, Jacobs, Mecke and Blossey2003).
Many films encountered in natural and industrial settings are, however, not planar. Typically, highly curved regions exist at the edges immediately after film formation, examples being the film between two foam bubbles, the wetting film between an elongated bubble and the walls of a non-circular capillary, the curved edges of a soap film supported on a wire frame, and the tear film on eye lids. These curved regions impose a localized pressure gradient that drains the film towards the curved edges. The dynamics of non-planar films is hence governed by two thinning mechanisms: (1) capillary thinning, i.e. drainage due to curvature differences and (2) spontaneous growth of fluctuations originating from thermal fluctuations. The interplay of these two thinning mechanisms is the subject of this paper.
Theory on the dynamics of films solely governed by drainage (and not by the spontaneous growth of fluctuations) goes back to Reynolds (Reference Reynolds1886), who modelled the drainage of a planar film as spatially uniform thinning caused by a prescribed pressure jump at the edge of the film. It is now known that non-planar films do not thin out uniformly unless they are, in some sense, small (Platikanov Reference Platikanov1964; Buevich & Lipkina Reference Buevich and Lipkina1975; Singh, Miller & Hirasaki Reference Singh, Miller and Hirasaki1997). Larger films develop a local depression called a dimple near the film edge that eventually leads to rupture (Frankel & Mysels Reference Frankel and Myseis1962). Joye, Hirasaki & Miller (Reference Joye, Hirasaki and Miller1992) determined a criterion for the thinning predominantly due to the formation of a dimple by comparing the curvature of the dimple with that of the meniscus. For many practical systems, this criterion gives us that films with a radius larger than about
![]() $50~\unicode[STIX]{x03BC}\text{m}$
have dimples (Malhotra & Wasan Reference Malhotra and Wasan1987; Manev, Tsekov & Radoev Reference Manev, Tsekov and Radoev1997). For such large films, our recent work (Kreutzer et al.
Reference Kreutzer, Shah, Parthiban and Khan2018) provides a scaling rule for the rupture times of unstable films with the relative strength of drainage and intermolecular forces as the key governing parameter. Here, we focus on this large-film limit, where thinning is non-uniform and confined to a dimple at the edge of the film.
$50~\unicode[STIX]{x03BC}\text{m}$
have dimples (Malhotra & Wasan Reference Malhotra and Wasan1987; Manev, Tsekov & Radoev Reference Manev, Tsekov and Radoev1997). For such large films, our recent work (Kreutzer et al.
Reference Kreutzer, Shah, Parthiban and Khan2018) provides a scaling rule for the rupture times of unstable films with the relative strength of drainage and intermolecular forces as the key governing parameter. Here, we focus on this large-film limit, where thinning is non-uniform and confined to a dimple at the edge of the film.
How the dynamics of non-planar films alters when, on top of drainage, thinning also occurs through the spontaneous growth of fluctuations is not yet fully understood. Vrij (Reference Vrij1966) and Scheludko (Reference Scheludko1967) attribute a crucial role to thermal fluctuations in the spontaneous growth of unstable waves leading to rupture. One of the seminal papers by Vrij (Reference Vrij1966) postulates that a film initially thins uniformly while all fluctuations are dampened until the stability flips as predicted from linear stability analysis. After this flip, a wave with growing amplitude fits within the length of the film such that the film ruptures at the trough of the wave. However, experimental observations have noted significant fluctuations in film thickness already from the onset of drainage, whether thermal (Radoev, Scheludko & Manev Reference Radoev, Scheludko and Manev1983) or hydrodynamic (Manev et al. Reference Manev, Tsekov and Radoev1997) in origin. Manev et al. (Reference Manev, Tsekov and Radoev1997) show in their experiments that these fluctuations do not dampen out if they are large enough, and attribute this to the large nonlinearities in the thin film equation. To account for the observed deviations between experiments and Reynolds’ theory, several theories have been developed that semi-empirically incorporate non-uniform thinning together with fluctuations in the description of planar film thinning (Sharma & Ruckenstein Reference Sharma and Ruckenstein1987; Tsekov & Ruckenstein Reference Tsekov and Ruckenstein1993; Manev et al. Reference Manev, Tsekov and Radoev1997; Manev & Nguyen Reference Manev and Nguyen2005). Although these theories are in reasonable agreement with experiments, they do not teach if and when rupture occurs through the formation of a dimple or due to the spontaneous growth of waves originating from thermal fluctuations, or are due to both. This lack of clarity is also reflected in the more recent literature; some studies emphasize the relevance of thermal fluctuations resulting in stochasticity in film rupture (Aarts & Lekkerkerker Reference Aarts and Lekkerkerker2008; Rio & Biance Reference Rio and Biance2014; Perumanath et al. Reference Perumanath, Borg, Chubynsky, Sprittles and Reese2019), whereas other studies argue that the influence of this stochastic phenomenon is insignificant (Vakarelski et al. Reference Vakarelski, Manica, Tang, O’Shea, Stevens, Grieser, Dagastine and Chan2010; Chan, Klaseboer & Manica Reference Chan, Klaseboer and Manica2011). Aarts & Lekkerkerker (Reference Aarts and Lekkerkerker2008) reported illustrative experiments of interfaces with ultra-low interfacial tension, which visually reveal the role of thermal fluctuations in inducing rupture. Rio & Biance (Reference Rio and Biance2014) in their review compare the order of magnitude of the time scales of drainage and of the spontaneous growth of thermal fluctuations, and suggest that stochastic rupture due to thermal fluctuations is relevant in determining film rupture times. Perumanath et al. (Reference Perumanath, Borg, Chubynsky, Sprittles and Reese2019) show using molecular dynamics simulations that, in the absence of film drainage, the onset of coalescence is a stochastic phenomenon triggered by thermal fluctuations. In contrast, Vakarelski et al. (Reference Vakarelski, Manica, Tang, O’Shea, Stevens, Grieser, Dagastine and Chan2010) and Chan et al. (Reference Chan, Klaseboer and Manica2011) argue that thermal fluctuations play no significant role in the rupture of films in parameter ranges typical for the coalescence of droplets and bubbles.
The aim of this work is to systematically study the dynamics of thin liquid films subjected to curvature-induced drainage for a wide parameter space in terms of drainage strength and thermal noise strength and to resolve when one of the two above-mentioned thinning mechanisms is dominant. The model geometry considered in this numerical study is a semi-infinite planar film connected to a curved film of constant curvature, known as a Plateau border. We incorporate thermal fluctuations at the gas–liquid interface using a stochastic term in the thin film equation (Davidovitch, Moro & Stone Reference Davidovitch, Moro and Stone2005; Grün et al. Reference Grün, Mecke and Rauscher2006), which allows us to study the effect of different strengths of thermal noise. Contrary to large films of finite size, as for the example found in Scheludko-cell experiments (e.g. Radoev et al. Reference Radoev, Scheludko and Manev1983; Manev, Sazdanova & Wasan Reference Manev, Sazdanova and Wasan1984; Coons et al. Reference Coons, Halley, McGlashan and Tran-Cong2003) in which dimple formation and thinning of the planar part of the film occur simultaneously leading to a complex dependency of rupture time on film size, we consider this semi-infinite geometry which evolves in the limit of full dimple formation, also known as marginal pinching (Aradian, Raphael & de Gennes Reference Aradian, Raphael and de Gennes2001). The selected geometry and a wide parameter space in terms of drainage strength and thermal noise strength defines the problem in its simplest form and allows us to resolve when, if and how thermal fluctuations are relevant in dimpled film rupture.
2 Problem formulation

Figure 1. Schematic of a non-flat draining thin film subjected to thermal fluctuations, with the film thickness parameterized by
![]() $h(x,t)$
. (a) The initial film shows a curved part extending from
$h(x,t)$
. (a) The initial film shows a curved part extending from
![]() $-l_{1}\leqslant x<0$
with the pressure given by the Laplace pressure,
$-l_{1}\leqslant x<0$
with the pressure given by the Laplace pressure,
![]() $p=-\unicode[STIX]{x1D6FE}/r$
, with
$p=-\unicode[STIX]{x1D6FE}/r$
, with
![]() $1/r$
as the curvature imposed at the edge. This curved part is connected to a flat part extending from
$1/r$
as the curvature imposed at the edge. This curved part is connected to a flat part extending from
![]() $0\leqslant x\leqslant l_{2}$
with the pressure given by the van der Waals component of the disjoining pressure,
$0\leqslant x\leqslant l_{2}$
with the pressure given by the van der Waals component of the disjoining pressure,
![]() $p=A/6\unicode[STIX]{x03C0}h^{3}$
. Besides curvature-induced drainage, the film is also subjected to thermal fluctuations of the free interface, resulting in thickness variations of amplitude
$p=A/6\unicode[STIX]{x03C0}h^{3}$
. Besides curvature-induced drainage, the film is also subjected to thermal fluctuations of the free interface, resulting in thickness variations of amplitude
![]() ${\sim}\sqrt{k_{B}T/\unicode[STIX]{x1D6FE}}$
. The dashed line at
${\sim}\sqrt{k_{B}T/\unicode[STIX]{x1D6FE}}$
. The dashed line at
![]() $x=l_{2}$
signifies the symmetry in the system. (b) Shape upon rupture, highlighting that film thinning stems from two competing mechanisms: (1) the formation of a localised dimple due to curvature-induced drainage and (2) the spontaneous growth of waves originating from thermal fluctuations.
$x=l_{2}$
signifies the symmetry in the system. (b) Shape upon rupture, highlighting that film thinning stems from two competing mechanisms: (1) the formation of a localised dimple due to curvature-induced drainage and (2) the spontaneous growth of waves originating from thermal fluctuations.
We study the evolution of non-flat thin liquid films with viscosity
![]() $\unicode[STIX]{x1D707}$
and surface tension
$\unicode[STIX]{x1D707}$
and surface tension
![]() $\unicode[STIX]{x1D6FE}$
, with the spatio-temporal film thickness parameterized by
$\unicode[STIX]{x1D6FE}$
, with the spatio-temporal film thickness parameterized by
![]() $h(x,t)$
, as shown in figure 1. The film is comprised of a curved part (
$h(x,t)$
, as shown in figure 1. The film is comprised of a curved part (
![]() $-l_{1}\leqslant x<0$
), with a curvature
$-l_{1}\leqslant x<0$
), with a curvature
![]() $1/r$
corresponding to a Plateau border, connected to a flat part (
$1/r$
corresponding to a Plateau border, connected to a flat part (
![]() $0\leqslant x\leqslant l_{2}$
). Considering the pressure in the gas phase to be uniform and setting it equal to zero, the pressure
$0\leqslant x\leqslant l_{2}$
). Considering the pressure in the gas phase to be uniform and setting it equal to zero, the pressure
![]() $p$
in the curved part of the liquid film, where intermolecular forces play an insignificant role, is dictated primarily by the Laplace pressure and is equal to
$p$
in the curved part of the liquid film, where intermolecular forces play an insignificant role, is dictated primarily by the Laplace pressure and is equal to
![]() $p=-\unicode[STIX]{x1D6FE}/r$
. Conversely, the pressure in the thin flat part is dictated by intermolecular forces, which in this paper, are considered as attractive van der Waals forces, such that
$p=-\unicode[STIX]{x1D6FE}/r$
. Conversely, the pressure in the thin flat part is dictated by intermolecular forces, which in this paper, are considered as attractive van der Waals forces, such that
![]() $p=A/6\unicode[STIX]{x03C0}h^{3}$
, with
$p=A/6\unicode[STIX]{x03C0}h^{3}$
, with
![]() $A<0$
being the Hamaker constant. The difference in pressure drains the liquid from the flatter part of the film to the more curved part. On top of this capillary thinning mechanism arising from curvature differences, a second thinning mechanism arises from the interplay between stabilizing surface tension forces and destabilizing van der Waals forces leading to the spontaneous growth of perturbations. These perturbations originate from thermal fluctuations at the gas–liquid interface causing corrugations of amplitude
$A<0$
being the Hamaker constant. The difference in pressure drains the liquid from the flatter part of the film to the more curved part. On top of this capillary thinning mechanism arising from curvature differences, a second thinning mechanism arises from the interplay between stabilizing surface tension forces and destabilizing van der Waals forces leading to the spontaneous growth of perturbations. These perturbations originate from thermal fluctuations at the gas–liquid interface causing corrugations of amplitude
![]() ${\sim}\sqrt{k_{B}T/\unicode[STIX]{x1D6FE}}$
. Depending on the relative strength between these two thinning mechanisms, the former may result in the formation of a dimple at the connection between the flat and curved part, while the later may result in the growth of unstable waves on the film interface.
${\sim}\sqrt{k_{B}T/\unicode[STIX]{x1D6FE}}$
. Depending on the relative strength between these two thinning mechanisms, the former may result in the formation of a dimple at the connection between the flat and curved part, while the later may result in the growth of unstable waves on the film interface.
The stochastic thin film equation that describes the evolution of non-planar thin films subjected to thermal fluctuations can be derived by applying a long-wave approximation on the incompressible Navier–Stokes equations with thermal noise (Grün et al. Reference Grün, Mecke and Rauscher2006). This yields
with the first term on the right-hand side arising from surface tension forces and the second term from long-ranged attractive van der Waals forces. Together with the transient term on the left-hand side, they comprise the well known deterministic thin film equation (Oron et al.
Reference Oron, Davis and Bankoff1997; Batchelor Reference Batchelor2000). The functional form of the noise term, i.e. the third term on the right-hand side, has been independently derived by Davidovitch et al. (Reference Davidovitch, Moro and Stone2005) and Grün et al. (Reference Grün, Mecke and Rauscher2006) using different approaches, with
![]() $\unicode[STIX]{x1D709}(x,t)$
constituting spatio-temporal Gaussian white noise consistent with the fluctuation-dissipation theorem. It possesses the following properties:
$\unicode[STIX]{x1D709}(x,t)$
constituting spatio-temporal Gaussian white noise consistent with the fluctuation-dissipation theorem. It possesses the following properties:
with
![]() $\unicode[STIX]{x1D6FF}(x-x^{\prime })$
in units
$\unicode[STIX]{x1D6FF}(x-x^{\prime })$
in units
![]() $1~\text{m}^{-2}$
, resulting from the reduction of the two-dimensional fluctuating hydrodynamics equations to one dimension (Grün et al.
Reference Grün, Mecke and Rauscher2006; Diez, González & Fernández Reference Diez, González and Fernández2016).
$1~\text{m}^{-2}$
, resulting from the reduction of the two-dimensional fluctuating hydrodynamics equations to one dimension (Grün et al.
Reference Grün, Mecke and Rauscher2006; Diez, González & Fernández Reference Diez, González and Fernández2016).
The initial film profile consists of a flat film connected to a parabola with constant curvature (
![]() $1/r$
), akin to a Plateau border. This yields the following initial condition:
$1/r$
), akin to a Plateau border. This yields the following initial condition:
As left far-field boundary conditions, we impose an interface shape with a constant curvature similar to the system studied by Aradian et al. (Reference Aradian, Raphael and de Gennes2001). We impose the boundary conditions at
![]() $x=-l_{1}$
, with
$x=-l_{1}$
, with
![]() $l_{1}$
chosen such that the profile remains essentially constant in time for
$l_{1}$
chosen such that the profile remains essentially constant in time for
![]() $x\ll 0$
, ensuring that the region of interest is connected to a practically static far-field profile. Note that, as usually tacitly assumed for thin-film dynamics between two far-field static profiles, the lubrication approximation needs to only hold in the transition region in-between the far-field limits (Bretherton Reference Bretherton1961). As right far-field boundary condition, we have zero gradients in thickness and pressure (at
$x\ll 0$
, ensuring that the region of interest is connected to a practically static far-field profile. Note that, as usually tacitly assumed for thin-film dynamics between two far-field static profiles, the lubrication approximation needs to only hold in the transition region in-between the far-field limits (Bretherton Reference Bretherton1961). As right far-field boundary condition, we have zero gradients in thickness and pressure (at
![]() $x=l_{2}$
), such that the problem is mirror symmetric around
$x=l_{2}$
), such that the problem is mirror symmetric around
![]() $x=l_{2}$
. The boundary conditions hence read
$x=l_{2}$
. The boundary conditions hence read
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle h(x=-l_{1},t)=h_{o}+\frac{x^{2}}{2r},\quad \frac{\unicode[STIX]{x2202}^{2}h}{\unicode[STIX]{x2202}x^{2}}(x=-l_{1},t)=\frac{1}{r},\\ \displaystyle \frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}x}(x=l_{2},t)=0,\quad \frac{\unicode[STIX]{x2202}^{3}h}{\unicode[STIX]{x2202}x^{3}}(x=l_{2},t)=0.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle h(x=-l_{1},t)=h_{o}+\frac{x^{2}}{2r},\quad \frac{\unicode[STIX]{x2202}^{2}h}{\unicode[STIX]{x2202}x^{2}}(x=-l_{1},t)=\frac{1}{r},\\ \displaystyle \frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}x}(x=l_{2},t)=0,\quad \frac{\unicode[STIX]{x2202}^{3}h}{\unicode[STIX]{x2202}x^{3}}(x=l_{2},t)=0.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
Using a height scale
![]() $h^{\ast }=h_{o}$
, an axial length scale
$h^{\ast }=h_{o}$
, an axial length scale
![]() $x^{\ast }=h_{0}^{2}\sqrt{2\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FE}/A}$
and a time scale
$x^{\ast }=h_{0}^{2}\sqrt{2\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FE}/A}$
and a time scale
![]() $t^{\ast }=12\unicode[STIX]{x03C0}^{2}\unicode[STIX]{x1D707}\unicode[STIX]{x1D6FE}h_{0}^{5}/A^{2}$
, we obtain the dimensionless variables
$t^{\ast }=12\unicode[STIX]{x03C0}^{2}\unicode[STIX]{x1D707}\unicode[STIX]{x1D6FE}h_{0}^{5}/A^{2}$
, we obtain the dimensionless variables
![]() $\tilde{h}=h/h^{\ast }$
,
$\tilde{h}=h/h^{\ast }$
,
![]() $\tilde{x}=x/x^{\ast }$
and
$\tilde{x}=x/x^{\ast }$
and
![]() $\tilde{t}=t/t^{\ast }$
together with the following dimensionless equations
$\tilde{t}=t/t^{\ast }$
together with the following dimensionless equations
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \tilde{h}(\tilde{x}=-\tilde{l_{1}},\tilde{t})=1+\unicode[STIX]{x1D705}\tilde{x}^{2},\quad \frac{\unicode[STIX]{x2202}^{2}\tilde{h}}{\unicode[STIX]{x2202}\tilde{x}^{2}}(\tilde{x}=-\tilde{l_{1}},\tilde{t})=2\unicode[STIX]{x1D705},\\[12.0pt] \displaystyle \frac{\unicode[STIX]{x2202}\tilde{h}}{\unicode[STIX]{x2202}\tilde{x}}(\tilde{x}=\tilde{l_{2}},\tilde{t})=0,\quad \frac{\unicode[STIX]{x2202}^{3}\tilde{h}}{\unicode[STIX]{x2202}\tilde{x}^{3}}(\tilde{x}=\tilde{l_{2}},\tilde{t})=0,\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \tilde{h}(\tilde{x}=-\tilde{l_{1}},\tilde{t})=1+\unicode[STIX]{x1D705}\tilde{x}^{2},\quad \frac{\unicode[STIX]{x2202}^{2}\tilde{h}}{\unicode[STIX]{x2202}\tilde{x}^{2}}(\tilde{x}=-\tilde{l_{1}},\tilde{t})=2\unicode[STIX]{x1D705},\\[12.0pt] \displaystyle \frac{\unicode[STIX]{x2202}\tilde{h}}{\unicode[STIX]{x2202}\tilde{x}}(\tilde{x}=\tilde{l_{2}},\tilde{t})=0,\quad \frac{\unicode[STIX]{x2202}^{3}\tilde{h}}{\unicode[STIX]{x2202}\tilde{x}^{3}}(\tilde{x}=\tilde{l_{2}},\tilde{t})=0,\end{array}\right\} & & \displaystyle\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D709}$
was made dimensionless using
$\unicode[STIX]{x1D709}$
was made dimensionless using
![]() $\tilde{\unicode[STIX]{x1D709}}=\unicode[STIX]{x1D709}/[\unicode[STIX]{x1D6FE}(h_{o}/x^{\ast })^{3}\sqrt{2\unicode[STIX]{x1D703}/3h_{o}}]$
and
$\tilde{\unicode[STIX]{x1D709}}=\unicode[STIX]{x1D709}/[\unicode[STIX]{x1D6FE}(h_{o}/x^{\ast })^{3}\sqrt{2\unicode[STIX]{x1D703}/3h_{o}}]$
and
![]() $l_{1}$
and
$l_{1}$
and
![]() $l_{2}$
using
$l_{2}$
using
![]() $x^{\ast }$
. This analysis shows that, besides the two parameters characterizing the domain length (
$x^{\ast }$
. This analysis shows that, besides the two parameters characterizing the domain length (
![]() $\tilde{l_{1}}$
and
$\tilde{l_{1}}$
and
![]() $\tilde{l_{2}}$
), the problem is fully governed by two dimensionless control parameters, the strength of drainage,
$\tilde{l_{2}}$
), the problem is fully governed by two dimensionless control parameters, the strength of drainage,
![]() $\unicode[STIX]{x1D705}=\unicode[STIX]{x03C0}h_{o}^{3}\unicode[STIX]{x1D6FE}/Ar$
, and the strength of thermal noise,
$\unicode[STIX]{x1D705}=\unicode[STIX]{x03C0}h_{o}^{3}\unicode[STIX]{x1D6FE}/Ar$
, and the strength of thermal noise,
![]() $\unicode[STIX]{x1D703}=k_{B}T/\unicode[STIX]{x1D6FE}h_{o}^{2}$
. The former describes the ratio between the imposed Laplace pressure that induces drainage, and the initial disjoining pressure arising from attractive van der Waals forces. The latter describes the square of the ratio between the amplitude of interface corrugations due to thermal fluctuations (
$\unicode[STIX]{x1D703}=k_{B}T/\unicode[STIX]{x1D6FE}h_{o}^{2}$
. The former describes the ratio between the imposed Laplace pressure that induces drainage, and the initial disjoining pressure arising from attractive van der Waals forces. The latter describes the square of the ratio between the amplitude of interface corrugations due to thermal fluctuations (
![]() $\sqrt{k_{B}T/\unicode[STIX]{x1D6FE}}$
) and the initial film thickness (
$\sqrt{k_{B}T/\unicode[STIX]{x1D6FE}}$
) and the initial film thickness (
![]() $h_{0}$
). We scan a wide range of values for
$h_{0}$
). We scan a wide range of values for
![]() $\unicode[STIX]{x1D705}$
(
$\unicode[STIX]{x1D705}$
(
![]() $10^{-5}-10^{3}$
) and
$10^{-5}-10^{3}$
) and
![]() $\unicode[STIX]{x1D703}$
(
$\unicode[STIX]{x1D703}$
(
![]() $4\times 10^{-5}-4\times 10^{-2}$
) with corresponding corrugations in thickness of
$4\times 10^{-5}-4\times 10^{-2}$
) with corresponding corrugations in thickness of
![]() $O(\sqrt{2\unicode[STIX]{x1D703}})$
. While typical experimental values for
$O(\sqrt{2\unicode[STIX]{x1D703}})$
. While typical experimental values for
![]() $\unicode[STIX]{x1D705}$
are
$\unicode[STIX]{x1D705}$
are
![]() $\unicode[STIX]{x1D705}\geqslant 10^{-1}$
and for
$\unicode[STIX]{x1D705}\geqslant 10^{-1}$
and for
![]() $\unicode[STIX]{x1D703}$
are
$\unicode[STIX]{x1D703}$
are
![]() $10^{-5}{-}10^{-3}$
, we do not restrict ourselves to this parameter space but perform a full parametric study.
$10^{-5}{-}10^{-3}$
, we do not restrict ourselves to this parameter space but perform a full parametric study.
Having formulated the problem, we describe the domain considerations to capture the relevant physics. The extent of
![]() $l_{1}$
needs to be larger than the transition region in which the curvature changes from practically zero at the flat part of the film to
$l_{1}$
needs to be larger than the transition region in which the curvature changes from practically zero at the flat part of the film to
![]() $1/r$
in the Plateau border. The dimensional length of this transition region is estimated to be
$1/r$
in the Plateau border. The dimensional length of this transition region is estimated to be
![]() ${\sim}\sqrt{h_{o}r}$
(Breward & Howell Reference Breward and Howell2002; Cantat et al.
Reference Cantat, Cohen-Addad, Elias, Graner, Höhler, Pitois, Rouyer and Saint-Jalmes2013), where
${\sim}\sqrt{h_{o}r}$
(Breward & Howell Reference Breward and Howell2002; Cantat et al.
Reference Cantat, Cohen-Addad, Elias, Graner, Höhler, Pitois, Rouyer and Saint-Jalmes2013), where
![]() $h_{o}$
is the initial film thickness. This gives the lower limit,
$h_{o}$
is the initial film thickness. This gives the lower limit,
![]() $l_{1}\gg \sqrt{h_{o}r}$
. The upper limit to the extent of
$l_{1}\gg \sqrt{h_{o}r}$
. The upper limit to the extent of
![]() $l_{1}$
is dictated by the geometric constraint of the long-wave approximation, i.e.
$l_{1}$
is dictated by the geometric constraint of the long-wave approximation, i.e.
![]() $\unicode[STIX]{x2202}_{x}h\ll 1$
. More specifically, the curvature as defined by
$\unicode[STIX]{x2202}_{x}h\ll 1$
. More specifically, the curvature as defined by
![]() $\unicode[STIX]{x2202}_{x}^{2}h/(1+(\unicode[STIX]{x2202}_{x}h)^{2})^{3/2}=1/r$
in the parabolic description of the Plateau border should be approximately equal to
$\unicode[STIX]{x2202}_{x}^{2}h/(1+(\unicode[STIX]{x2202}_{x}h)^{2})^{3/2}=1/r$
in the parabolic description of the Plateau border should be approximately equal to
![]() $\unicode[STIX]{x2202}_{x}^{2}h\approx 1/r$
as assumed in the boundary condition, equation (2.4). Estimating
$\unicode[STIX]{x2202}_{x}^{2}h\approx 1/r$
as assumed in the boundary condition, equation (2.4). Estimating
![]() $\unicode[STIX]{x2202}_{x}h$
as
$\unicode[STIX]{x2202}_{x}h$
as
![]() $x/r$
from (2.3) and setting
$x/r$
from (2.3) and setting
![]() $x=l_{1}$
, this directly gives the upper limit,
$x=l_{1}$
, this directly gives the upper limit,
![]() $l_{1}\ll r$
. Taken together,
$l_{1}\ll r$
. Taken together,
![]() $\sqrt{1/2\unicode[STIX]{x1D705}}\ll l_{1}\ll \sqrt{r/2h_{o}\unicode[STIX]{x1D705}}$
gives the lower and upper limit to
$\sqrt{1/2\unicode[STIX]{x1D705}}\ll l_{1}\ll \sqrt{r/2h_{o}\unicode[STIX]{x1D705}}$
gives the lower and upper limit to
![]() $l_{1}$
in dimensionless form. The extent of
$l_{1}$
in dimensionless form. The extent of
![]() $l_{2}$
is chosen such that at least one fastest-growing wave, arising from the interplay between the stabilizing surface tension forces and destabilizing van der Waals forces, fits within the film, i.e.
$l_{2}$
is chosen such that at least one fastest-growing wave, arising from the interplay between the stabilizing surface tension forces and destabilizing van der Waals forces, fits within the film, i.e.
![]() $l_{2}\geqslant \unicode[STIX]{x1D706}_{max}$
, with the wavelength of the fastest-growing wave (
$l_{2}\geqslant \unicode[STIX]{x1D706}_{max}$
, with the wavelength of the fastest-growing wave (
![]() $\unicode[STIX]{x1D706}_{max}$
) estimated in the next section. All parameters and variables are made dimensionless from this point on and we therefore drop the tilde in the rest of the paper.
$\unicode[STIX]{x1D706}_{max}$
) estimated in the next section. All parameters and variables are made dimensionless from this point on and we therefore drop the tilde in the rest of the paper.
We conclude this section by noting that the chosen geometry allows us to study two types of systems: (1) the film between two two-dimensional bubbles with rigid interfaces (as may be encountered in surfactant-rich systems) and (2) the film between a surfactant-free bubble and a solid wall, as for example encountered between an elongated bubble and the walls of a non-circular microchannel. In that case, a nearly flat film in the central part of the channel connects to a meniscus at the corners of the channel, with the curvature of the meniscus primarily imposed by the dimensions of the channel (Wong, Radke & Morris Reference Wong, Radke and Morris1995; Khodaparast et al.
Reference Khodaparast, Atasi, Deblais, Scheid and Stone2018). In the first system, the free interface at
![]() $y=h(x,t)$
is described by the commonly encountered tangentially immobile boundary condition (Chan et al.
Reference Chan, Klaseboer and Manica2011), i.e. no-slip, while a symmetry boundary condition, i.e. no-shear, is used at
$y=h(x,t)$
is described by the commonly encountered tangentially immobile boundary condition (Chan et al.
Reference Chan, Klaseboer and Manica2011), i.e. no-slip, while a symmetry boundary condition, i.e. no-shear, is used at
![]() $y=0$
. In the second system, the free interface is described by a no-shear condition and the wall by a no-slip condition. Although the boundary conditions for the velocity at the top and bottom of the domain are reversed for these two systems, their dynamics is described by one and the same thin film equation and the results presented throughout this paper are equally valid for both types of system.
$y=0$
. In the second system, the free interface is described by a no-shear condition and the wall by a no-slip condition. Although the boundary conditions for the velocity at the top and bottom of the domain are reversed for these two systems, their dynamics is described by one and the same thin film equation and the results presented throughout this paper are equally valid for both types of system.
3 Linear stability analysis
As an input to our numerical implementation in choosing a film large enough to accommodate a fastest-growing wave, we study how small perturbations develop on a planar thin film using linear stability theory. We consider a film of initially uniform thickness
![]() $h(x,t=0)=1$
, subjected to perturbation of amplitude
$h(x,t=0)=1$
, subjected to perturbation of amplitude
![]() $\unicode[STIX]{x1D716}\ll 1$
. Its response to these perturbations, represented by waves of wavelength
$\unicode[STIX]{x1D716}\ll 1$
. Its response to these perturbations, represented by waves of wavelength
![]() $\unicode[STIX]{x1D706}$
, wave number
$\unicode[STIX]{x1D706}$
, wave number
![]() $k=2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D706}$
and growth rate
$k=2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D706}$
and growth rate
![]() $\unicode[STIX]{x1D714}$
, is found by substituting
$\unicode[STIX]{x1D714}$
, is found by substituting
![]() $h(x,t)=h(x,t=0)+\unicode[STIX]{x1D716}\text{e}^{\text{i}kx+\unicode[STIX]{x1D714}t}$
in the noise-free equivalent of (2.5). In this analysis,
$h(x,t)=h(x,t=0)+\unicode[STIX]{x1D716}\text{e}^{\text{i}kx+\unicode[STIX]{x1D714}t}$
in the noise-free equivalent of (2.5). In this analysis,
![]() $h(x,t)$
was made dimensionless using
$h(x,t)$
was made dimensionless using
![]() $h^{\ast }$
,
$h^{\ast }$
,
![]() $\unicode[STIX]{x1D706}$
using
$\unicode[STIX]{x1D706}$
using
![]() $x^{\ast }$
,
$x^{\ast }$
,
![]() $k$
using
$k$
using
![]() $1/x^{\ast }$
, and
$1/x^{\ast }$
, and
![]() $\unicode[STIX]{x1D714}$
using
$\unicode[STIX]{x1D714}$
using
![]() $1/t^{\ast }$
. Linearizing the resulting expression to
$1/t^{\ast }$
. Linearizing the resulting expression to
![]() $O(\unicode[STIX]{x1D716})$
yields the dimensionless dispersion relation
$O(\unicode[STIX]{x1D716})$
yields the dimensionless dispersion relation
The film is unstable for all
![]() $k$
s corresponding to
$k$
s corresponding to
![]() $\unicode[STIX]{x1D714}>0$
, and stable otherwise. The wave that grows fastest and dominates the other waves has a wavenumber
$\unicode[STIX]{x1D714}>0$
, and stable otherwise. The wave that grows fastest and dominates the other waves has a wavenumber
![]() $k_{max}=1/\sqrt{2}$
, with corresponding wavelength
$k_{max}=1/\sqrt{2}$
, with corresponding wavelength
![]() $\unicode[STIX]{x1D706}_{max}=2\unicode[STIX]{x03C0}/k_{max}=2\sqrt{2}\unicode[STIX]{x03C0}\approx 8.8$
and growth rate
$\unicode[STIX]{x1D706}_{max}=2\unicode[STIX]{x03C0}/k_{max}=2\sqrt{2}\unicode[STIX]{x03C0}\approx 8.8$
and growth rate
![]() $\unicode[STIX]{x1D714}_{max}=1/4$
. The time,
$\unicode[STIX]{x1D714}_{max}=1/4$
. The time,
![]() $t_{r}$
required for the film to rupture due to the spontaneous growth of the perturbations is hence of order of magnitude,
$t_{r}$
required for the film to rupture due to the spontaneous growth of the perturbations is hence of order of magnitude,
![]() $t_{r}\sim 1/\unicode[STIX]{x1D714}_{max}=4$
. How this time depends on the magnitude of the initial perturbations is estimated by considering when the magnitude of the perturbation due to the fastest-growing wave, i.e.
$t_{r}\sim 1/\unicode[STIX]{x1D714}_{max}=4$
. How this time depends on the magnitude of the initial perturbations is estimated by considering when the magnitude of the perturbation due to the fastest-growing wave, i.e.
![]() $\unicode[STIX]{x1D716}\text{e}^{\unicode[STIX]{x1D714}_{max}t_{r}}$
, is of the order of
$\unicode[STIX]{x1D716}\text{e}^{\unicode[STIX]{x1D714}_{max}t_{r}}$
, is of the order of
![]() $h(x,t=0)=1$
. As the initial perturbations originate from thermal noise, such that
$h(x,t=0)=1$
. As the initial perturbations originate from thermal noise, such that
![]() $\unicode[STIX]{x1D716}$
can be approximated with the amplitude
$\unicode[STIX]{x1D716}$
can be approximated with the amplitude
![]() $\sqrt{2\unicode[STIX]{x1D703}}$
in (2.5), the time
$\sqrt{2\unicode[STIX]{x1D703}}$
in (2.5), the time
![]() $t_{r}$
required for the film to rupture due to the spontaneous growth of thermal fluctuations is hence of order of magnitude
$t_{r}$
required for the film to rupture due to the spontaneous growth of thermal fluctuations is hence of order of magnitude
4 Numerical implementation
We numerically solved the one-dimensional stochastic thin film equation (2.5) along with its initial and boundary conditions (2.7–2.8) using a finite difference method. We discretized the domain into an equidistant mesh of size,
![]() $\unicode[STIX]{x0394}x$
, using a second-order central differencing scheme for spatial discretization and an implicit–explicit time differencing scheme of a constant time step size,
$\unicode[STIX]{x0394}x$
, using a second-order central differencing scheme for spatial discretization and an implicit–explicit time differencing scheme of a constant time step size,
![]() $\unicode[STIX]{x0394}t$
, with a theoretical order of accuracy of
$\unicode[STIX]{x0394}t$
, with a theoretical order of accuracy of
![]() $O(\unicode[STIX]{x0394}t^{0.5})$
(Lord, Powell & Shardlow Reference Lord, Powell and Shardlow2014). The curved part extends from
$O(\unicode[STIX]{x0394}t^{0.5})$
(Lord, Powell & Shardlow Reference Lord, Powell and Shardlow2014). The curved part extends from
![]() $-l_{1}\leqslant x<0$
and the flat part from
$-l_{1}\leqslant x<0$
and the flat part from
![]() $0\leqslant x\leqslant l_{2}$
, resulting in
$0\leqslant x\leqslant l_{2}$
, resulting in
![]() $N=(l_{1}+l_{2})/\unicode[STIX]{x0394}x+1$
grid points.
$N=(l_{1}+l_{2})/\unicode[STIX]{x0394}x+1$
grid points.
We discuss the domain considerations based on the constraints described in § 2. For the parabolic film profile at
![]() $-l_{1}\leqslant x<0$
, we require
$-l_{1}\leqslant x<0$
, we require
![]() $\sqrt{1/2\unicode[STIX]{x1D705}}\ll l_{1}\ll \sqrt{r/2h_{o}\unicode[STIX]{x1D705}}$
. We confirm that rupture times and rupture locations are insensitive to the chosen value when chosen within this range. For
$\sqrt{1/2\unicode[STIX]{x1D705}}\ll l_{1}\ll \sqrt{r/2h_{o}\unicode[STIX]{x1D705}}$
. We confirm that rupture times and rupture locations are insensitive to the chosen value when chosen within this range. For
![]() $\unicode[STIX]{x1D705}\leqslant 0.1$
, we used
$\unicode[STIX]{x1D705}\leqslant 0.1$
, we used
![]() $l_{1}=300$
, while smaller values were used for larger
$l_{1}=300$
, while smaller values were used for larger
![]() $\unicode[STIX]{x1D705}$
. For the flat part, we used
$\unicode[STIX]{x1D705}$
. For the flat part, we used
![]() $l_{2}=240$
, which is much larger compared to the wavelength of the fastest-growing wave (
$l_{2}=240$
, which is much larger compared to the wavelength of the fastest-growing wave (
![]() $\unicode[STIX]{x1D706}_{max}=8.8$
), as determined using a linear stability analysis. We note that, for large
$\unicode[STIX]{x1D706}_{max}=8.8$
), as determined using a linear stability analysis. We note that, for large
![]() $\unicode[STIX]{x1D705}\gg 1$
, shorter
$\unicode[STIX]{x1D705}\gg 1$
, shorter
![]() $l_{2}$
captures the relevant physics as well, so long as at least one fastest-growing wave can be expressed in it. For small
$l_{2}$
captures the relevant physics as well, so long as at least one fastest-growing wave can be expressed in it. For small
![]() $\unicode[STIX]{x1D705}\ll 1$
, we will show later that the results weakly depend on
$\unicode[STIX]{x1D705}\ll 1$
, we will show later that the results weakly depend on
![]() $l_{2}$
, even though
$l_{2}$
, even though
![]() $l_{2}\gg \unicode[STIX]{x1D706}_{max}$
.
$l_{2}\gg \unicode[STIX]{x1D706}_{max}$
.
Time discretization of the stochastic thin film equation (2.5) is performed using an implicit–explicit scheme, wherein the fourth-order term describing the capillary forces is discretized implicitly. The terms describing the nonlinear van der Waals forces and the stochastic noise are discretized explicitly. The mobility term in the deterministic part (
![]() $h^{3}$
) is discretized as per the positivity-preserving scheme described by Diez, Kondic & Bertozzi (Reference Diez, Kondic and Bertozzi2000). Such a scheme is not required in discretizing the square root of the mobility term in the stochastic part (
$h^{3}$
) is discretized as per the positivity-preserving scheme described by Diez, Kondic & Bertozzi (Reference Diez, Kondic and Bertozzi2000). Such a scheme is not required in discretizing the square root of the mobility term in the stochastic part (
![]() $h^{3/2}$
) (Grün et al.
Reference Grün, Mecke and Rauscher2006), and therefore we discretize it using a standard central differencing scheme.
$h^{3/2}$
) (Grün et al.
Reference Grün, Mecke and Rauscher2006), and therefore we discretize it using a standard central differencing scheme.
The stochastic term,
![]() $\unicode[STIX]{x1D709}(x,t)$
, is expanded as per separation of variables in the Q-Wiener process, and further based on the lemmas given in Grün et al. (Reference Grün, Mecke and Rauscher2006), as follows:
$\unicode[STIX]{x1D709}(x,t)$
, is expanded as per separation of variables in the Q-Wiener process, and further based on the lemmas given in Grün et al. (Reference Grün, Mecke and Rauscher2006), as follows:
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D709}(x,t)=\frac{\unicode[STIX]{x2202}W(x,t)}{\unicode[STIX]{x2202}t}=\mathop{\sum }_{q\rightarrow -\infty }^{q\rightarrow \infty }\unicode[STIX]{x1D712}_{q}\dot{\unicode[STIX]{x1D6FD}_{q}}(t)g_{q}(x)\approx \mathop{\sum }_{q=-\frac{N-1}{2}}^{q=\frac{N-1}{2}}\unicode[STIX]{x1D712}_{q}\dot{\unicode[STIX]{x1D6FD}_{q}}(t)g_{q}(x), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D709}(x,t)=\frac{\unicode[STIX]{x2202}W(x,t)}{\unicode[STIX]{x2202}t}=\mathop{\sum }_{q\rightarrow -\infty }^{q\rightarrow \infty }\unicode[STIX]{x1D712}_{q}\dot{\unicode[STIX]{x1D6FD}_{q}}(t)g_{q}(x)\approx \mathop{\sum }_{q=-\frac{N-1}{2}}^{q=\frac{N-1}{2}}\unicode[STIX]{x1D712}_{q}\dot{\unicode[STIX]{x1D6FD}_{q}}(t)g_{q}(x), & \displaystyle\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D712}_{q}$
is a measure of spatial correlation (with
$\unicode[STIX]{x1D712}_{q}$
is a measure of spatial correlation (with
![]() $\unicode[STIX]{x1D712}_{q}=1$
for spatially uncorrelated systems, as considered in this paper).
$\unicode[STIX]{x1D712}_{q}=1$
for spatially uncorrelated systems, as considered in this paper).
![]() $\dot{\unicode[STIX]{x1D6FD}_{q}}$
corresponds to white-noise processes in time, where the term
$\dot{\unicode[STIX]{x1D6FD}_{q}}$
corresponds to white-noise processes in time, where the term
![]() $\unicode[STIX]{x1D6FD}_{q}(t_{n+1})-\unicode[STIX]{x1D6FD}_{q}(t_{n})$
is normally distributed with variance given by the time increment,
$\unicode[STIX]{x1D6FD}_{q}(t_{n+1})-\unicode[STIX]{x1D6FD}_{q}(t_{n})$
is normally distributed with variance given by the time increment,
![]() $\unicode[STIX]{x0394}t$
(Grün et al.
Reference Grün, Mecke and Rauscher2006; Lord et al.
Reference Lord, Powell and Shardlow2014). Here
$\unicode[STIX]{x0394}t$
(Grün et al.
Reference Grün, Mecke and Rauscher2006; Lord et al.
Reference Lord, Powell and Shardlow2014). Here
![]() ${\mathcal{N}}_{q}^{n}$
are computer-generated normally distributed random numbers (using the randn MATLAB routine), which are approximately distributed with a mean of 0 and standard deviation of 1. The term
${\mathcal{N}}_{q}^{n}$
are computer-generated normally distributed random numbers (using the randn MATLAB routine), which are approximately distributed with a mean of 0 and standard deviation of 1. The term
![]() $g_{q}(x)$
corresponds to the set of orthonormal eigenfunctions (Grün et al.
Reference Grün, Mecke and Rauscher2006; Diez et al.
Reference Diez, González and Fernández2016) according to
$g_{q}(x)$
corresponds to the set of orthonormal eigenfunctions (Grün et al.
Reference Grün, Mecke and Rauscher2006; Diez et al.
Reference Diez, González and Fernández2016) according to
 $$\begin{eqnarray}\displaystyle g_{q}(x)=\left\{\begin{array}{@{}ll@{}}\displaystyle \sqrt{\frac{2}{L}}\sin \left(\frac{2\unicode[STIX]{x03C0}qx}{L}\right),\quad & \text{for }q<0,\\ \displaystyle \sqrt{\frac{1}{L}},\quad & \text{for }q=0,\\ \displaystyle \sqrt{\frac{2}{L}}\cos \left(\frac{2\unicode[STIX]{x03C0}qx}{L}\right),\quad & \text{for }q>0,\end{array}\right. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g_{q}(x)=\left\{\begin{array}{@{}ll@{}}\displaystyle \sqrt{\frac{2}{L}}\sin \left(\frac{2\unicode[STIX]{x03C0}qx}{L}\right),\quad & \text{for }q<0,\\ \displaystyle \sqrt{\frac{1}{L}},\quad & \text{for }q=0,\\ \displaystyle \sqrt{\frac{2}{L}}\cos \left(\frac{2\unicode[STIX]{x03C0}qx}{L}\right),\quad & \text{for }q>0,\end{array}\right. & & \displaystyle\end{eqnarray}$$
with
![]() $L$
the dimensionless domain size equal to
$L$
the dimensionless domain size equal to
![]() $l_{1}+l_{2}$
. The resulting discrete noise term equals
$l_{1}+l_{2}$
. The resulting discrete noise term equals
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D709}(x,t)=\frac{1}{\sqrt{\unicode[STIX]{x0394}t}}\mathop{\sum }_{q=-\frac{N-1}{2}}^{q=\frac{N-1}{2}}{\mathcal{N}}_{q}^{n}g_{q}(x). & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D709}(x,t)=\frac{1}{\sqrt{\unicode[STIX]{x0394}t}}\mathop{\sum }_{q=-\frac{N-1}{2}}^{q=\frac{N-1}{2}}{\mathcal{N}}_{q}^{n}g_{q}(x). & \displaystyle\end{eqnarray}$$
We note here that in our finding an upwind discretization of the noise term, as proposed in Grün et al. (Reference Grün, Mecke and Rauscher2006), led to time step size dependent results of the rupture times. Therefore we used a central differencing scheme to discretize the stochastic term. Using
![]() $\unicode[STIX]{x0394}x=0.05$
and
$\unicode[STIX]{x0394}x=0.05$
and
![]() $\unicode[STIX]{x0394}t=\unicode[STIX]{x0394}x^{2.75}$
for
$\unicode[STIX]{x0394}t=\unicode[STIX]{x0394}x^{2.75}$
for
![]() $\unicode[STIX]{x1D705}\leqslant 10^{-1}$
, and
$\unicode[STIX]{x1D705}\leqslant 10^{-1}$
, and
![]() $\unicode[STIX]{x0394}x=0.005$
and
$\unicode[STIX]{x0394}x=0.005$
and
![]() $\unicode[STIX]{x0394}t=\unicode[STIX]{x0394}x^{3.25}$
for
$\unicode[STIX]{x0394}t=\unicode[STIX]{x0394}x^{3.25}$
for
![]() $\unicode[STIX]{x1D705}>10^{-1}$
, the presented simulation results for rupture times are grid and time step size independent within
$\unicode[STIX]{x1D705}>10^{-1}$
, the presented simulation results for rupture times are grid and time step size independent within
![]() $5\,\%$
, as can be seen from figure 7 in the Appendix for the smallest and the largest value of
$5\,\%$
, as can be seen from figure 7 in the Appendix for the smallest and the largest value of
![]() $\unicode[STIX]{x1D705}$
considered in this work. The number of realizations for noise-inclusive simulations obtained for different values of the governing parameters
$\unicode[STIX]{x1D705}$
considered in this work. The number of realizations for noise-inclusive simulations obtained for different values of the governing parameters
![]() $\unicode[STIX]{x1D705}$
and
$\unicode[STIX]{x1D705}$
and
![]() $\unicode[STIX]{x1D703}$
is 400, with different seeds for every realization. This yields a sampling error in mean and standard deviation of reported rupture times below
$\unicode[STIX]{x1D703}$
is 400, with different seeds for every realization. This yields a sampling error in mean and standard deviation of reported rupture times below
![]() $1/\sqrt{400}\triangleq 5\,\%$
, see figure 8 in the Appendix. Error bars in figures 5–7 represent one standard deviation.
$1/\sqrt{400}\triangleq 5\,\%$
, see figure 8 in the Appendix. Error bars in figures 5–7 represent one standard deviation.
5 Results
5.1 Transition between thinning mechanisms
A signifying feature of draining thin films as compared to their non-draining counterparts is the formation of a local depression. This so-called dimple (Joye et al.
Reference Joye, Hirasaki and Miller1992; Aradian et al.
Reference Aradian, Raphael and de Gennes2001) results from the localized non-zero pressure gradient at the location where the flat part of the film connects to the curved part (in this study, at
![]() $x=0$
). We start with an estimate of the dimensionless curvature,
$x=0$
). We start with an estimate of the dimensionless curvature,
![]() $\unicode[STIX]{x1D705}_{tr}$
at which the time scale for film rupture as a result of curvature-induced drainage is comparable to the time scale for film rupture as a result of the growth of fluctuations due to the interplay between surface tension and van der Waals forces. An estimate for
$\unicode[STIX]{x1D705}_{tr}$
at which the time scale for film rupture as a result of curvature-induced drainage is comparable to the time scale for film rupture as a result of the growth of fluctuations due to the interplay between surface tension and van der Waals forces. An estimate for
![]() $\unicode[STIX]{x1D705}_{tr}$
is obtained by comparing the time scale for the dimple formation and that for the growth of fluctuations. The former is calculated as
$\unicode[STIX]{x1D705}_{tr}$
is obtained by comparing the time scale for the dimple formation and that for the growth of fluctuations. The former is calculated as
![]() $t_{r}\sim 1.05\unicode[STIX]{x1D705}^{-10/7}$
for
$t_{r}\sim 1.05\unicode[STIX]{x1D705}^{-10/7}$
for
![]() $\unicode[STIX]{x1D705}\gg \unicode[STIX]{x1D705}_{tr}$
in Kreutzer et al. (Reference Kreutzer, Shah, Parthiban and Khan2018) and the latter is calculated as
$\unicode[STIX]{x1D705}\gg \unicode[STIX]{x1D705}_{tr}$
in Kreutzer et al. (Reference Kreutzer, Shah, Parthiban and Khan2018) and the latter is calculated as
![]() $t_{r}\approx -4\ln (\sqrt{2\unicode[STIX]{x1D703}})$
(see § 3), independent of
$t_{r}\approx -4\ln (\sqrt{2\unicode[STIX]{x1D703}})$
(see § 3), independent of
![]() $\unicode[STIX]{x1D705}$
. Matching these two time scales, for realistic noise strengths of
$\unicode[STIX]{x1D705}$
. Matching these two time scales, for realistic noise strengths of
![]() $\unicode[STIX]{x1D703}=10^{-5}{-}10^{-3}$
, gives
$\unicode[STIX]{x1D703}=10^{-5}{-}10^{-3}$
, gives
![]() $\unicode[STIX]{x1D705}_{tr}\approx 0.1$
at which the transition between the two thinning mechanisms occurs.
$\unicode[STIX]{x1D705}_{tr}\approx 0.1$
at which the transition between the two thinning mechanisms occurs.

Figure 2. Film dynamics for
![]() $\unicode[STIX]{x1D705}=0.1$
, i.e. close to the transition curvature where the time scale for rupture due to drainage is comparable to the time scale for rupture due to the spontaneous growth of fluctuations. (a) Film evolution in space (zoomed here close to
$\unicode[STIX]{x1D705}=0.1$
, i.e. close to the transition curvature where the time scale for rupture due to drainage is comparable to the time scale for rupture due to the spontaneous growth of fluctuations. (a) Film evolution in space (zoomed here close to
![]() $x\sim 0$
) and time (for
$x\sim 0$
) and time (for
![]() $t=0$
, 1.37, 3.00, 3.14) for noise-free (deterministic) simulation (
$t=0$
, 1.37, 3.00, 3.14) for noise-free (deterministic) simulation (
![]() $\unicode[STIX]{x1D703}=0$
). (b) Single realisation of the noise-inclusive counterpart of (a) for
$\unicode[STIX]{x1D703}=0$
). (b) Single realisation of the noise-inclusive counterpart of (a) for
![]() $\unicode[STIX]{x1D703}=0.001$
. The insets in (a) and (b) show the time evolution of the minimum film height,
$\unicode[STIX]{x1D703}=0.001$
. The insets in (a) and (b) show the time evolution of the minimum film height,
![]() $h_{min}$
. (c) Film evolution for 400 realizations of the same simulations as in (b), with the minimum film heights being extrapolated from their last recorded (
$h_{min}$
. (c) Film evolution for 400 realizations of the same simulations as in (b), with the minimum film heights being extrapolated from their last recorded (
![]() $h_{min}\lesssim 0.05$
) values to 0. The insets represent the distributions of times required to reach the three indicated heights, one in early drainage-governed stage, a second at the late disjoining pressure-governed stage, and a third at the crossover of these stages. (d) Standard deviation in the time required to reach a given minimum height as obtained from the 400 realizations of (c).
$h_{min}\lesssim 0.05$
) values to 0. The insets represent the distributions of times required to reach the three indicated heights, one in early drainage-governed stage, a second at the late disjoining pressure-governed stage, and a third at the crossover of these stages. (d) Standard deviation in the time required to reach a given minimum height as obtained from the 400 realizations of (c).
We first analyse film rupture at
![]() $\unicode[STIX]{x1D705}\approx \unicode[STIX]{x1D705}_{tr}$
. Figure 2(a) shows the film evolution for a (noise-free) deterministic simulation (
$\unicode[STIX]{x1D705}\approx \unicode[STIX]{x1D705}_{tr}$
. Figure 2(a) shows the film evolution for a (noise-free) deterministic simulation (
![]() $\unicode[STIX]{x1D703}=0$
). The film profiles
$\unicode[STIX]{x1D703}=0$
). The film profiles
![]() $h(x,t)$
illustrate the formation of a dimple at
$h(x,t)$
illustrate the formation of a dimple at
![]() $x\sim 0$
, while the film remains flat far from the dimple. Further characterizing the film dynamics based on the minimum film height,
$x\sim 0$
, while the film remains flat far from the dimple. Further characterizing the film dynamics based on the minimum film height,
![]() $h_{min}(t)$
, as shown in the inset, we observe that its evolution consists of two stages: (i) an early stage primarily governed by drainage, roughly between
$h_{min}(t)$
, as shown in the inset, we observe that its evolution consists of two stages: (i) an early stage primarily governed by drainage, roughly between
![]() $1\geqslant h_{min}\gtrsim 0.8$
, with a thinning rate that decreases in time as discussed in Aradian et al. (Reference Aradian, Raphael and de Gennes2001), and (ii) a late stage governed by the disjoining pressure, for
$1\geqslant h_{min}\gtrsim 0.8$
, with a thinning rate that decreases in time as discussed in Aradian et al. (Reference Aradian, Raphael and de Gennes2001), and (ii) a late stage governed by the disjoining pressure, for
![]() $h_{min}\lesssim 0.8$
, with the thinning rate rapidly increasing prior to rupture as discussed in Zhang & Lister (Reference Zhang and Lister1999).
$h_{min}\lesssim 0.8$
, with the thinning rate rapidly increasing prior to rupture as discussed in Zhang & Lister (Reference Zhang and Lister1999).
How the addition of thermal noise alters the film dynamics is shown in figure 2(b) for a single realization of a noise-inclusive simulation with a noise strength
![]() $\unicode[STIX]{x1D703}=0.001$
. The film evolves with the formation of a dimple at
$\unicode[STIX]{x1D703}=0.001$
. The film evolves with the formation of a dimple at
![]() $x\sim 0$
, similar to what is seen in figure 2(a) for the deterministic counterpart. However, it also illustrates the growth of fluctuations, resulting in the formation of a wave in the flat portion of the film, thereby indicating a competition between the two thinning mechanisms. The minimum film height shown in the inset decreases similarly to the deterministic counterpart, but with the noise superimposed over it. An additional consequence of the inclusion of noise is the spread in film evolution as shown for 400 realizations in figure 2(c). The curves show that most of the spread occurs in the early drainage stage. This is more clearly seen from the three insets, which show histograms of the time required to reach the three indicated minimum heights. These distributions appear normal and were used to further characterize the spread in evolution by computing the standard deviation as a function of
$x\sim 0$
, similar to what is seen in figure 2(a) for the deterministic counterpart. However, it also illustrates the growth of fluctuations, resulting in the formation of a wave in the flat portion of the film, thereby indicating a competition between the two thinning mechanisms. The minimum film height shown in the inset decreases similarly to the deterministic counterpart, but with the noise superimposed over it. An additional consequence of the inclusion of noise is the spread in film evolution as shown for 400 realizations in figure 2(c). The curves show that most of the spread occurs in the early drainage stage. This is more clearly seen from the three insets, which show histograms of the time required to reach the three indicated minimum heights. These distributions appear normal and were used to further characterize the spread in evolution by computing the standard deviation as a function of
![]() $h_{min}$
, as shown in figure 2(d). The rupture times,
$h_{min}$
, as shown in figure 2(d). The rupture times,
![]() $t_{r}$
, of all realizations were calculated as the time at which the minimum film height first reaches
$t_{r}$
, of all realizations were calculated as the time at which the minimum film height first reaches
![]() $h_{min}(t=t_{r})=0.05$
. We note that the reported results for
$h_{min}(t=t_{r})=0.05$
. We note that the reported results for
![]() $t_{r}$
are insensitive to our chosen value of 0.05, because of the rapid evolution prior to rupture. For the presented case with
$t_{r}$
are insensitive to our chosen value of 0.05, because of the rapid evolution prior to rupture. For the presented case with
![]() $\unicode[STIX]{x1D705}=0.1$
, we find
$\unicode[STIX]{x1D705}=0.1$
, we find
![]() $t_{r}=3.11\pm 0.32$
(mean
$t_{r}=3.11\pm 0.32$
(mean
![]() $\pm$
standard deviation) for the noise-inclusive simulation with
$\pm$
standard deviation) for the noise-inclusive simulation with
![]() $\unicode[STIX]{x1D703}=0.001$
, with the mean value close to the noise-free (
$\unicode[STIX]{x1D703}=0.001$
, with the mean value close to the noise-free (
![]() $\unicode[STIX]{x1D703}=0$
) rupture time,
$\unicode[STIX]{x1D703}=0$
) rupture time,
![]() $t_{r}=3.14$
.
$t_{r}=3.14$
.

Figure 3. Comparison between films with high (
![]() $\unicode[STIX]{x1D705}\gg \unicode[STIX]{x1D705}_{tr}$
, dimple-dominated) and low (
$\unicode[STIX]{x1D705}\gg \unicode[STIX]{x1D705}_{tr}$
, dimple-dominated) and low (
![]() $\unicode[STIX]{x1D705}\ll \unicode[STIX]{x1D705}_{tr}$
, fluctuations-dominated) curvature, without (
$\unicode[STIX]{x1D705}\ll \unicode[STIX]{x1D705}_{tr}$
, fluctuations-dominated) curvature, without (
![]() $\unicode[STIX]{x1D703}=0$
) and with realistic (
$\unicode[STIX]{x1D703}=0$
) and with realistic (
![]() $\unicode[STIX]{x1D703}=0.001$
) noise. (a) Evolution of film heights in the dimple region for
$\unicode[STIX]{x1D703}=0.001$
) noise. (a) Evolution of film heights in the dimple region for
![]() $\unicode[STIX]{x1D705}=50$
for a deterministic simulation, at various dimensionless times
$\unicode[STIX]{x1D705}=50$
for a deterministic simulation, at various dimensionless times
![]() $t=(0.01,0.03,0.08,0.16,0.28,0.45,0.75,1.3,2.1,2.5)\times 10^{-3}$
(also reported in Kreutzer et al. (Reference Kreutzer, Shah, Parthiban and Khan2018)); (b) evolution of film heights in the dimple region for
$t=(0.01,0.03,0.08,0.16,0.28,0.45,0.75,1.3,2.1,2.5)\times 10^{-3}$
(also reported in Kreutzer et al. (Reference Kreutzer, Shah, Parthiban and Khan2018)); (b) evolution of film heights in the dimple region for
![]() $\unicode[STIX]{x1D705}=50$
for a single realization of a stochastic simulation, at various dimensionless times
$\unicode[STIX]{x1D705}=50$
for a single realization of a stochastic simulation, at various dimensionless times
![]() $t=(0.01,0.02,0.07,0.14,0.28,0.5,0.87,1.4,2.0,2.3)\times 10^{-3}$
. (c) evolution of film heights for
$t=(0.01,0.02,0.07,0.14,0.28,0.5,0.87,1.4,2.0,2.3)\times 10^{-3}$
. (c) evolution of film heights for
![]() $\unicode[STIX]{x1D705}=0.001$
for deterministic simulations, at various dimensionless times,
$\unicode[STIX]{x1D705}=0.001$
for deterministic simulations, at various dimensionless times,
![]() $t=(7,10,13.6,14.7,15.2,15.5,15.55,15.58,15.6)$
; (d) evolution of film heights for
$t=(7,10,13.6,14.7,15.2,15.5,15.55,15.58,15.6)$
; (d) evolution of film heights for
![]() $\unicode[STIX]{x1D705}=0.001$
for a single realization of a stochastic simulation at various dimensionless times,
$\unicode[STIX]{x1D705}=0.001$
for a single realization of a stochastic simulation at various dimensionless times,
![]() $t=(1.6,3,5.04,5.7,6.16,6.27,6.37)$
. The insets in (a–d) show the corresponding time evolutions of the minimum film height.
$t=(1.6,3,5.04,5.7,6.16,6.27,6.37)$
. The insets in (a–d) show the corresponding time evolutions of the minimum film height.

Figure 4. Comparison of rupture location between noise-free (
![]() $\unicode[STIX]{x1D703}=0$
) and noise-inclusive (
$\unicode[STIX]{x1D703}=0$
) and noise-inclusive (
![]() $\unicode[STIX]{x1D703}=0.001$
) evolutions as a function of curvature. The rupture locations for the noise-inclusive evolutions are illustrated as individual data points for 100 out of 400 realizations. The rupture locations for
$\unicode[STIX]{x1D703}=0.001$
) evolutions as a function of curvature. The rupture locations for the noise-inclusive evolutions are illustrated as individual data points for 100 out of 400 realizations. The rupture locations for
![]() $\unicode[STIX]{x1D703}=0$
and
$\unicode[STIX]{x1D703}=0$
and
![]() $\unicode[STIX]{x1D703}=0.001$
are shifted horizontally for better visibility.
$\unicode[STIX]{x1D703}=0.001$
are shifted horizontally for better visibility.
5.2 Influence of thermal fluctuations on film rupture at far limits of
 $\unicode[STIX]{x1D705}$
$\unicode[STIX]{x1D705}$
Having analysed film rupture for
![]() $\unicode[STIX]{x1D705}\approx \unicode[STIX]{x1D705}_{tr}$
, we now proceed to try to understand how thermal fluctuations influence the film break-up in the limit of high (
$\unicode[STIX]{x1D705}\approx \unicode[STIX]{x1D705}_{tr}$
, we now proceed to try to understand how thermal fluctuations influence the film break-up in the limit of high (
![]() $\gg \unicode[STIX]{x1D705}_{tr}$
) and low (
$\gg \unicode[STIX]{x1D705}_{tr}$
) and low (
![]() $\ll \unicode[STIX]{x1D705}_{tr}$
)
$\ll \unicode[STIX]{x1D705}_{tr}$
)
![]() $\unicode[STIX]{x1D705}$
, comparing these limits without (
$\unicode[STIX]{x1D705}$
, comparing these limits without (
![]() $\unicode[STIX]{x1D703}=0$
) and with realistic (
$\unicode[STIX]{x1D703}=0$
) and with realistic (
![]() $\unicode[STIX]{x1D703}=0.001$
) thermal noise. For strong drainage (
$\unicode[STIX]{x1D703}=0.001$
) thermal noise. For strong drainage (
![]() $\unicode[STIX]{x1D705}=50$
), we find that the film ruptures due to the formation of a dimple, with the spatio-temporal film profiles being almost indistinguishable for the noise-inclusive and noise-free case, see figures 3(a) and 3(b), respectively. This negligible influence of thermal fluctuations is as expected, because the time scale for dimple formation is much smaller compared to the time scale for the spontaneous growth of fluctuations for
$\unicode[STIX]{x1D705}=50$
), we find that the film ruptures due to the formation of a dimple, with the spatio-temporal film profiles being almost indistinguishable for the noise-inclusive and noise-free case, see figures 3(a) and 3(b), respectively. This negligible influence of thermal fluctuations is as expected, because the time scale for dimple formation is much smaller compared to the time scale for the spontaneous growth of fluctuations for
![]() $\unicode[STIX]{x1D705}\gg \unicode[STIX]{x1D705}_{tr}$
, as explained before. In this dimple-dominated regime, the resulting rupture time is insensitive to the addition of noise, with rupture times
$\unicode[STIX]{x1D705}\gg \unicode[STIX]{x1D705}_{tr}$
, as explained before. In this dimple-dominated regime, the resulting rupture time is insensitive to the addition of noise, with rupture times
![]() $t_{r}=2.5\times 10^{-3}\pm 8.7\times 10^{-5}$
for the noise-inclusive case and
$t_{r}=2.5\times 10^{-3}\pm 8.7\times 10^{-5}$
for the noise-inclusive case and
![]() $t_{r}=2.5\times 10^{-3}$
for the noise-free counterpart. Further characterization of the thinning dynamics in terms of
$t_{r}=2.5\times 10^{-3}$
for the noise-free counterpart. Further characterization of the thinning dynamics in terms of
![]() $h_{min}$
shows that the height of the dimple initially decreases as
$h_{min}$
shows that the height of the dimple initially decreases as
![]() $h_{min}\sim t^{-1/2}$
for both the noise-free and noise-inclusive case, see the insets in figures 3(a) and 3(b), in agreement with earlier theoretical work (Aradian et al.
Reference Aradian, Raphael and de Gennes2001).
$h_{min}\sim t^{-1/2}$
for both the noise-free and noise-inclusive case, see the insets in figures 3(a) and 3(b), in agreement with earlier theoretical work (Aradian et al.
Reference Aradian, Raphael and de Gennes2001).
For weak drainage (
![]() $\unicode[STIX]{x1D705}=0.001$
), rather than through the formation of a dimple, film rupture is initiated by the growth of unstable waves on the planar portion of the film, akin to what is observed for de-wetting of thin planar films (Grün et al.
Reference Grün, Mecke and Rauscher2006; Diez et al.
Reference Diez, González and Fernández2016). In this fluctuations-dominated regime, the film evolution exhibits the growth of a dominant unstable wave, which grows fastest close to
$\unicode[STIX]{x1D705}=0.001$
), rather than through the formation of a dimple, film rupture is initiated by the growth of unstable waves on the planar portion of the film, akin to what is observed for de-wetting of thin planar films (Grün et al.
Reference Grün, Mecke and Rauscher2006; Diez et al.
Reference Diez, González and Fernández2016). In this fluctuations-dominated regime, the film evolution exhibits the growth of a dominant unstable wave, which grows fastest close to
![]() $x=0$
due to the small dimple that still forms there which triggers the accelerated growth of the wave at that location. For the noise-free case, rupture occurs at
$x=0$
due to the small dimple that still forms there which triggers the accelerated growth of the wave at that location. For the noise-free case, rupture occurs at
![]() $x\approx -2.5$
(figure 3
c), i.e. within half a wavelength of the fastest-growing wave (
$x\approx -2.5$
(figure 3
c), i.e. within half a wavelength of the fastest-growing wave (
![]() $\unicode[STIX]{x1D706}_{max}=8.8$
) from
$\unicode[STIX]{x1D706}_{max}=8.8$
) from
![]() $x=0$
. The inset shows an almost dormant initial evolution of the film, with little decrease in film height due to drainage for
$x=0$
. The inset shows an almost dormant initial evolution of the film, with little decrease in film height due to drainage for
![]() $(t_{r}-t)>5$
, followed by a rapid decrease in film height due to the van der Waals forces. In this stage, the film height evolves with the earlier reported theoretical scaling,
$(t_{r}-t)>5$
, followed by a rapid decrease in film height due to the van der Waals forces. In this stage, the film height evolves with the earlier reported theoretical scaling,
![]() $h_{min}\sim (t_{r}-t)^{1/5}$
(Zhang & Lister Reference Zhang and Lister1999), see the inset of figure 3(c). Interestingly, the addition of thermal noise to films exhibiting weak drainage results in rupture locations away from
$h_{min}\sim (t_{r}-t)^{1/5}$
(Zhang & Lister Reference Zhang and Lister1999), see the inset of figure 3(c). Interestingly, the addition of thermal noise to films exhibiting weak drainage results in rupture locations away from
![]() $x=0$
, see figure 3(d). The film instability is initiated due to the growth of an unstable dominant wave, like the noise-free evolution. However, due to the presence of noise everywhere along the film, rupture can occur at any of the valleys of the wave that grows fastest. Comparing the dynamics of the film evolution for the noise-inclusive case with that of the noise-free case, we see no dormant initial phase in the inset of figure 3(d). This is because the amplitude of the corrugations resulting from thermal noise is orders of magnitude larger compared to the initial perturbation in the noise-free case, where spontaneous growth of unstable waves originates from the non-uniform initial shape of the film. This leads to shorter rupture times for the noise-inclusive case yielding
$x=0$
, see figure 3(d). The film instability is initiated due to the growth of an unstable dominant wave, like the noise-free evolution. However, due to the presence of noise everywhere along the film, rupture can occur at any of the valleys of the wave that grows fastest. Comparing the dynamics of the film evolution for the noise-inclusive case with that of the noise-free case, we see no dormant initial phase in the inset of figure 3(d). This is because the amplitude of the corrugations resulting from thermal noise is orders of magnitude larger compared to the initial perturbation in the noise-free case, where spontaneous growth of unstable waves originates from the non-uniform initial shape of the film. This leads to shorter rupture times for the noise-inclusive case yielding
![]() $t_{r}=6.95\pm 0.68$
versus
$t_{r}=6.95\pm 0.68$
versus
![]() $t_{r}=15.6$
for noise-free case.
$t_{r}=15.6$
for noise-free case.
5.3 Influence of thermal fluctuations on rupture locations
Having established that the film ruptures through the formation of a dimple at
![]() $x\sim 0$
for strong drainage (
$x\sim 0$
for strong drainage (
![]() $\unicode[STIX]{x1D705}\gg \unicode[STIX]{x1D705}_{tr}$
) and through the spontaneous growth of fluctuations at a random location for weak drainage (
$\unicode[STIX]{x1D705}\gg \unicode[STIX]{x1D705}_{tr}$
) and through the spontaneous growth of fluctuations at a random location for weak drainage (
![]() $\unicode[STIX]{x1D705}\ll \unicode[STIX]{x1D705}_{tr}$
), we now further detail the influence of thermal fluctuations on rupture location for the whole range of curvatures. Without noise, the film ruptures through the formation of a dimple at
$\unicode[STIX]{x1D705}\ll \unicode[STIX]{x1D705}_{tr}$
), we now further detail the influence of thermal fluctuations on rupture location for the whole range of curvatures. Without noise, the film ruptures through the formation of a dimple at
![]() $x_{r}\approx 0$
within one grid point, see the crosses in figure 4. With noise, the film also ruptures at
$x_{r}\approx 0$
within one grid point, see the crosses in figure 4. With noise, the film also ruptures at
![]() $x_{r}\approx 0$
for strong drainage, while rupture occurs at a random location for weak drainage, with
$x_{r}\approx 0$
for strong drainage, while rupture occurs at a random location for weak drainage, with
![]() $x_{r}$
being uniformly distributed over the flat portion of the film without any preference for the location where the dimple would otherwise grow. The differences in rupture locations between films with strong and weak drainage can be used to explain the experimental observations of films being ruptured always at the rim (Frankel & Mysels Reference Frankel and Myseis1962) or at random locations (Aarts & Lekkerkerker Reference Aarts and Lekkerkerker2008). As expected, based on the earlier presented analysis of time scales, figure 4 clearly illustrates that
$x_{r}$
being uniformly distributed over the flat portion of the film without any preference for the location where the dimple would otherwise grow. The differences in rupture locations between films with strong and weak drainage can be used to explain the experimental observations of films being ruptured always at the rim (Frankel & Mysels Reference Frankel and Myseis1962) or at random locations (Aarts & Lekkerkerker Reference Aarts and Lekkerkerker2008). As expected, based on the earlier presented analysis of time scales, figure 4 clearly illustrates that
![]() $\unicode[STIX]{x1D705}_{tr}\approx 0.1$
marks the transition between the dimple-dominated regime (
$\unicode[STIX]{x1D705}_{tr}\approx 0.1$
marks the transition between the dimple-dominated regime (
![]() $\unicode[STIX]{x1D705}\gg \unicode[STIX]{x1D705}_{tr}$
) and the fluctuations-dominated regime (
$\unicode[STIX]{x1D705}\gg \unicode[STIX]{x1D705}_{tr}$
) and the fluctuations-dominated regime (
![]() $\unicode[STIX]{x1D705}\ll \unicode[STIX]{x1D705}_{tr}$
). We note that for the lowest values of
$\unicode[STIX]{x1D705}\ll \unicode[STIX]{x1D705}_{tr}$
). We note that for the lowest values of
![]() $\unicode[STIX]{x1D705}$
, the film not only ruptures at the flat portion of the film, but also occasionally at the curved portion (
$\unicode[STIX]{x1D705}$
, the film not only ruptures at the flat portion of the film, but also occasionally at the curved portion (
![]() $x<0$
) in the Plateau border.
$x<0$
) in the Plateau border.
5.4 Influence of thermal fluctuations on rupture time

Figure 5. (a) Dependence of rupture time on drainage (
![]() $\unicode[STIX]{x1D705}$
) and noise strength (
$\unicode[STIX]{x1D705}$
) and noise strength (
![]() $\unicode[STIX]{x1D703}$
). Two clearly separated regimes are visible wherein film thinning is dominated by dimple formation for high curvatures (
$\unicode[STIX]{x1D703}$
). Two clearly separated regimes are visible wherein film thinning is dominated by dimple formation for high curvatures (
![]() $\unicode[STIX]{x1D705}\gg \unicode[STIX]{x1D705}_{tr}$
) or by the growth of fluctuations for low curvatures (
$\unicode[STIX]{x1D705}\gg \unicode[STIX]{x1D705}_{tr}$
) or by the growth of fluctuations for low curvatures (
![]() $\unicode[STIX]{x1D705}\ll \unicode[STIX]{x1D705}_{tr}$
). Inset: rupture times rescaled with
$\unicode[STIX]{x1D705}\ll \unicode[STIX]{x1D705}_{tr}$
). Inset: rupture times rescaled with
![]() $1/\unicode[STIX]{x1D714}_{max}$
at
$1/\unicode[STIX]{x1D714}_{max}$
at
![]() $\unicode[STIX]{x1D705}=1\times 10^{-5}$
(highlighted by the ellipse) for different noise strengths. The observed slope is close to
$\unicode[STIX]{x1D705}=1\times 10^{-5}$
(highlighted by the ellipse) for different noise strengths. The observed slope is close to
![]() $-1$
as indicated by the triangle. We excluded the rupture time for the noise strength of
$-1$
as indicated by the triangle. We excluded the rupture time for the noise strength of
![]() $\unicode[STIX]{x1D703}=0.04$
in the fit, because the fluctuations of the interface
$\unicode[STIX]{x1D703}=0.04$
in the fit, because the fluctuations of the interface
![]() ${\sim}\sqrt{2\unicode[STIX]{x1D703}}$
are approximately
${\sim}\sqrt{2\unicode[STIX]{x1D703}}$
are approximately
![]() $30\,\%$
of the initial film thickness and the time for them to develop into the fastest-growing wave with
$30\,\%$
of the initial film thickness and the time for them to develop into the fastest-growing wave with
![]() $\unicode[STIX]{x1D714}_{max}=1/4$
is significantly longer than the film rupture time itself. (b) Transition curvature,
$\unicode[STIX]{x1D714}_{max}=1/4$
is significantly longer than the film rupture time itself. (b) Transition curvature,
![]() $\unicode[STIX]{x1D705}_{tr}$
, from dimple-dominated rupture to fluctuations-dominated rupture versus noise strength, with the inset showing how
$\unicode[STIX]{x1D705}_{tr}$
, from dimple-dominated rupture to fluctuations-dominated rupture versus noise strength, with the inset showing how
![]() $\unicode[STIX]{x1D705}_{tr}$
is calculated based on the film rupture times.
$\unicode[STIX]{x1D705}_{tr}$
is calculated based on the film rupture times.
We now study how thermal fluctuations influence the rupture time for different strengths of drainage. Figure 5(a) shows that the presence of noise does not significantly affect the rupture time and its earlier reported scaling with curvature (Kreutzer et al.
Reference Kreutzer, Shah, Parthiban and Khan2018) for
![]() $\unicode[STIX]{x1D705}\gg \unicode[STIX]{x1D705}_{tr}$
. By contrast, rupture times for
$\unicode[STIX]{x1D705}\gg \unicode[STIX]{x1D705}_{tr}$
. By contrast, rupture times for
![]() $\unicode[STIX]{x1D705}\ll \unicode[STIX]{x1D705}_{tr}$
depend strongly on noise strength and not on drainage strength, with higher noise strength resulting in shorter rupture times. Since the dominant thinning mechanism for low
$\unicode[STIX]{x1D705}\ll \unicode[STIX]{x1D705}_{tr}$
depend strongly on noise strength and not on drainage strength, with higher noise strength resulting in shorter rupture times. Since the dominant thinning mechanism for low
![]() $\unicode[STIX]{x1D705}$
is through the spontaneous growth of fluctuations and not through the formation of a dimple, there is no fundamental mechanistic difference between non-planar films with weak drainage
$\unicode[STIX]{x1D705}$
is through the spontaneous growth of fluctuations and not through the formation of a dimple, there is no fundamental mechanistic difference between non-planar films with weak drainage
![]() $\unicode[STIX]{x1D705}\ll 1$
and flat films without drainage
$\unicode[STIX]{x1D705}\ll 1$
and flat films without drainage
![]() $\unicode[STIX]{x1D705}=0$
, with the rupture times for low
$\unicode[STIX]{x1D705}=0$
, with the rupture times for low
![]() $\unicode[STIX]{x1D705}$
approaching those of flat films (with periodic boundary conditions). We note here that the rupture times in the fluctuations-dominated regime depend weakly on the choice of
$\unicode[STIX]{x1D705}$
approaching those of flat films (with periodic boundary conditions). We note here that the rupture times in the fluctuations-dominated regime depend weakly on the choice of
![]() $l_{2}$
, see figure 6 in Appendix. This is easily understood from the fact that, with increasing
$l_{2}$
, see figure 6 in Appendix. This is easily understood from the fact that, with increasing
![]() $l_{2}$
, the number of valleys of the dominant wave increases, thereby increasing the probability for the fastest possible rupture. An estimate for the rupture time for a truly semi-infinite film, i.e.
$l_{2}$
, the number of valleys of the dominant wave increases, thereby increasing the probability for the fastest possible rupture. An estimate for the rupture time for a truly semi-infinite film, i.e.
![]() $l_{2}\rightarrow \infty$
, is hence obtained by considering the minima of rupture times in a sufficiently large ensemble of evolutions for the fluctuations-dominated regime.
$l_{2}\rightarrow \infty$
, is hence obtained by considering the minima of rupture times in a sufficiently large ensemble of evolutions for the fluctuations-dominated regime.
How rupture times depend on noise strength for a given value of
![]() $\unicode[STIX]{x1D705}$
is next examined. We rationalized that the rupture time scales with noise strength according to
$\unicode[STIX]{x1D705}$
is next examined. We rationalized that the rupture time scales with noise strength according to
![]() $\unicode[STIX]{x1D714}_{max}t_{r}\sim \ln (\sqrt{2\unicode[STIX]{x1D703}})^{-1}$
, see (3.2). This prediction agrees well with simulation results for which we obtain
$\unicode[STIX]{x1D714}_{max}t_{r}\sim \ln (\sqrt{2\unicode[STIX]{x1D703}})^{-1}$
, see (3.2). This prediction agrees well with simulation results for which we obtain
![]() $\unicode[STIX]{x1D714}_{max}t_{r}\sim \ln (\sqrt{2\unicode[STIX]{x1D703}})^{-1.15\pm 0.04}$
for
$\unicode[STIX]{x1D714}_{max}t_{r}\sim \ln (\sqrt{2\unicode[STIX]{x1D703}})^{-1.15\pm 0.04}$
for
![]() $\unicode[STIX]{x1D705}=10^{-5}$
, see the inset of figure 5(a). We attribute this small difference primarily to the overprediction of the rupture time by applying linear theory to a full nonlinear problem. Finally, figure 5(b) shows how the transition curvature
$\unicode[STIX]{x1D705}=10^{-5}$
, see the inset of figure 5(a). We attribute this small difference primarily to the overprediction of the rupture time by applying linear theory to a full nonlinear problem. Finally, figure 5(b) shows how the transition curvature
![]() $\unicode[STIX]{x1D705}_{tr}$
, marking the transition from the dimple-dominated regime to the fluctuations-dominated regime depends on noise strength, with
$\unicode[STIX]{x1D705}_{tr}$
, marking the transition from the dimple-dominated regime to the fluctuations-dominated regime depends on noise strength, with
![]() $\unicode[STIX]{x1D705}_{tr}$
calculated as shown in the inset. For realistic
$\unicode[STIX]{x1D705}_{tr}$
calculated as shown in the inset. For realistic
![]() $\unicode[STIX]{x1D703}$
between
$\unicode[STIX]{x1D703}$
between
![]() $10^{-5}$
and
$10^{-5}$
and
![]() $10^{-3}$
, this transition only weakly depends on
$10^{-3}$
, this transition only weakly depends on
![]() $\unicode[STIX]{x1D703}$
, and the earlier estimated transition
$\unicode[STIX]{x1D703}$
, and the earlier estimated transition
![]() $\unicode[STIX]{x1D705}_{tr}=0.1$
provides a good estimate for most experimentally relevant conditions.
$\unicode[STIX]{x1D705}_{tr}=0.1$
provides a good estimate for most experimentally relevant conditions.
6 Conclusions
We studied the evolution of draining non-planar thin films under the influence of thermal fluctuations for the large-film limit, where drainage is confined to a dimple. The central question answered in this paper is what role thermal fluctuations play in determining lifetimes of such films. The two key parameters governing this problem are the strength of drainage (
![]() $\unicode[STIX]{x1D705}$
) and the strength of thermal noise (
$\unicode[STIX]{x1D705}$
) and the strength of thermal noise (
![]() $\unicode[STIX]{x1D703}$
). For strong drainage,
$\unicode[STIX]{x1D703}$
). For strong drainage,
![]() $\unicode[STIX]{x1D705}\gg \unicode[STIX]{x1D705}_{tr}$
, our simulations show that the film ruptures deterministically due to rupture in the thinnest part of the dimple, regardless of
$\unicode[STIX]{x1D705}\gg \unicode[STIX]{x1D705}_{tr}$
, our simulations show that the film ruptures deterministically due to rupture in the thinnest part of the dimple, regardless of
![]() $\unicode[STIX]{x1D705}$
and
$\unicode[STIX]{x1D705}$
and
![]() $\unicode[STIX]{x1D703}$
. The rupture time then is as reported earlier (Kreutzer et al.
Reference Kreutzer, Shah, Parthiban and Khan2018), leaving no room for thermal fluctuations to grow and moderate the rupture process, in contrast to the concept of thermally induced rupture from some critical moment onwards. By contrast, for weak drainage,
$\unicode[STIX]{x1D703}$
. The rupture time then is as reported earlier (Kreutzer et al.
Reference Kreutzer, Shah, Parthiban and Khan2018), leaving no room for thermal fluctuations to grow and moderate the rupture process, in contrast to the concept of thermally induced rupture from some critical moment onwards. By contrast, for weak drainage,
![]() $\unicode[STIX]{x1D705}\ll \unicode[STIX]{x1D705}_{tr}$
, the film ruptures through the spontaneous growth of waves originating from thermal fluctuations. Rupture occurs at one of the valleys of the dominant wave, anywhere along the planar portion of the film. The mean rupture times are found to be independent of
$\unicode[STIX]{x1D705}\ll \unicode[STIX]{x1D705}_{tr}$
, the film ruptures through the spontaneous growth of waves originating from thermal fluctuations. Rupture occurs at one of the valleys of the dominant wave, anywhere along the planar portion of the film. The mean rupture times are found to be independent of
![]() $\unicode[STIX]{x1D705}$
and are well predicted by linear stability analysis as
$\unicode[STIX]{x1D705}$
and are well predicted by linear stability analysis as
![]() $t_{r}\approx 1/\unicode[STIX]{x1D714}_{max}\ln (\sqrt{2\unicode[STIX]{x1D703}})^{-1}$
. The transition between the dimple-dominated regime (
$t_{r}\approx 1/\unicode[STIX]{x1D714}_{max}\ln (\sqrt{2\unicode[STIX]{x1D703}})^{-1}$
. The transition between the dimple-dominated regime (
![]() $\unicode[STIX]{x1D705}\gg \unicode[STIX]{x1D705}_{tr}$
) and the fluctuations-dominated regime (
$\unicode[STIX]{x1D705}\gg \unicode[STIX]{x1D705}_{tr}$
) and the fluctuations-dominated regime (
![]() $\unicode[STIX]{x1D705}\ll \unicode[STIX]{x1D705}_{tr}$
) is around
$\unicode[STIX]{x1D705}\ll \unicode[STIX]{x1D705}_{tr}$
) is around
![]() $\unicode[STIX]{x1D705}_{tr}=0.1$
, with a weak dependence on noise strength.
$\unicode[STIX]{x1D705}_{tr}=0.1$
, with a weak dependence on noise strength.
Our work explains if, when and why it is important to include thermal fluctuations in the dynamics of draining thin films to predict where and when they rupture. We reiterate that our work focuses on the large film limit. Experimental data sets obtained in Scheludko cells (e.g. Radoev et al. Reference Radoev, Scheludko and Manev1983; Manev et al. Reference Manev, Sazdanova and Wasan1984; Manev & Nguyen Reference Manev and Nguyen2005) are for films in which drainage in the planar portion of the film occurs simultaneously with dimpled thinning. A direct comparison to those experiments requires including the film size as an additional parameter, which is beyond the scope of the present paper.
Acknowledgements
This work is supported by the Netherlands Organization for Scientific Research (NWO) and the Dutch Institute for Sustainable Process Technology (ISPT) as part of the project COFILM.
Appendix
Figure 6 shows how rupture times for the fluctuations-dominated (low
![]() $\unicode[STIX]{x1D705}$
) regime depend on the extent of flat portion of the film,
$\unicode[STIX]{x1D705}$
) regime depend on the extent of flat portion of the film,
![]() $l_{2}$
, with its mean and standard deviation decreasing by about
$l_{2}$
, with its mean and standard deviation decreasing by about
![]() $22\,\%$
and
$22\,\%$
and
![]() $84\,\%$
, respectively, when
$84\,\%$
, respectively, when
![]() $l_{2}$
is increased from 60 to 960. Figure 7 shows a grid and time step size dependency study, for
$l_{2}$
is increased from 60 to 960. Figure 7 shows a grid and time step size dependency study, for
![]() $\unicode[STIX]{x1D705}=10^{-5}$
and
$\unicode[STIX]{x1D705}=10^{-5}$
and
![]() $\unicode[STIX]{x1D705}=10^{3}$
. In the spirit of Grün et al. (Reference Grün, Mecke and Rauscher2006), we used a time step
$\unicode[STIX]{x1D705}=10^{3}$
. In the spirit of Grün et al. (Reference Grün, Mecke and Rauscher2006), we used a time step
![]() $\unicode[STIX]{x0394}t=\unicode[STIX]{x0394}x^{\unicode[STIX]{x1D6FC}}$
, for which we determined the values of
$\unicode[STIX]{x0394}t=\unicode[STIX]{x0394}x^{\unicode[STIX]{x1D6FC}}$
, for which we determined the values of
![]() $\unicode[STIX]{x1D6FC}$
empirically, varying
$\unicode[STIX]{x1D6FC}$
empirically, varying
![]() $\unicode[STIX]{x1D6FC}$
between 2.25 and 3 for the fluctuations-dominated regime and between 3.25 and 4 for the dimple-dominated regime. In the fluctuations-dominated regime, i.e. at low
$\unicode[STIX]{x1D6FC}$
between 2.25 and 3 for the fluctuations-dominated regime and between 3.25 and 4 for the dimple-dominated regime. In the fluctuations-dominated regime, i.e. at low
![]() $\unicode[STIX]{x1D705}$
, the analysis shows that a combination of a grid size of
$\unicode[STIX]{x1D705}$
, the analysis shows that a combination of a grid size of
![]() $\unicode[STIX]{x0394}x=0.05$
and a time step size of
$\unicode[STIX]{x0394}x=0.05$
and a time step size of
![]() $\unicode[STIX]{x0394}t=\unicode[STIX]{x0394}x^{2.75}$
provides a rupture time within
$\unicode[STIX]{x0394}t=\unicode[STIX]{x0394}x^{2.75}$
provides a rupture time within
![]() $5\,\%$
of the smallest grid and time step size used. For the dimple-dominated (high
$5\,\%$
of the smallest grid and time step size used. For the dimple-dominated (high
![]() $\unicode[STIX]{x1D705}$
) regime, a similar accuracy is obtained for
$\unicode[STIX]{x1D705}$
) regime, a similar accuracy is obtained for
![]() $\unicode[STIX]{x0394}x=0.005$
and
$\unicode[STIX]{x0394}x=0.005$
and
![]() $\unicode[STIX]{x0394}t=\unicode[STIX]{x0394}x^{3.25}$
. Figure 8 shows how the mean and standard deviation of the rupture time depend on the number of realisations, again for
$\unicode[STIX]{x0394}t=\unicode[STIX]{x0394}x^{3.25}$
. Figure 8 shows how the mean and standard deviation of the rupture time depend on the number of realisations, again for
![]() $\unicode[STIX]{x1D705}=10^{-5}$
and
$\unicode[STIX]{x1D705}=10^{-5}$
and
![]() $\unicode[STIX]{x1D705}=10^{3}$
. It shows that after about 300 realizations, the mean and the standard deviation are within 2 % and 5 %, respectively, of the values obtained for all 400 realizations.
$\unicode[STIX]{x1D705}=10^{3}$
. It shows that after about 300 realizations, the mean and the standard deviation are within 2 % and 5 %, respectively, of the values obtained for all 400 realizations.

Figure 6. Dependence of rupture time on the extent of the flat portion of the film,
![]() $l_{2}$
for
$l_{2}$
for
![]() $\unicode[STIX]{x1D703}=0.001$
and
$\unicode[STIX]{x1D703}=0.001$
and
![]() $\unicode[STIX]{x1D705}=10^{-5}$
.
$\unicode[STIX]{x1D705}=10^{-5}$
.

Figure 7. Dependence of rupture time on grid and time step size for noise-inclusive simulations (
![]() $\unicode[STIX]{x1D703}=0.001$
) for (a)
$\unicode[STIX]{x1D703}=0.001$
) for (a)
![]() $\unicode[STIX]{x1D705}=10^{-5}$
and (b)
$\unicode[STIX]{x1D705}=10^{-5}$
and (b)
![]() $\unicode[STIX]{x1D705}=10^{3}$
. Error bars were horizontally shifted for better visibility.
$\unicode[STIX]{x1D705}=10^{3}$
. Error bars were horizontally shifted for better visibility.

Figure 8. Statistical significance based on the number of realizations. Mean rupture times (
![]() $\unicode[STIX]{x1D707}_{tr}$
) (a,b) and corresponding standard deviation (
$\unicode[STIX]{x1D707}_{tr}$
) (a,b) and corresponding standard deviation (
![]() $\unicode[STIX]{x1D70E}_{tr}$
) (c,d) as a function of the number of realizations randomly picked from a pool of 400 noise-inclusive simulations (
$\unicode[STIX]{x1D70E}_{tr}$
) (c,d) as a function of the number of realizations randomly picked from a pool of 400 noise-inclusive simulations (
![]() $\unicode[STIX]{x1D703}=0.001$
) for
$\unicode[STIX]{x1D703}=0.001$
) for
![]() $\unicode[STIX]{x1D705}=10^{-5}$
(a,c) and
$\unicode[STIX]{x1D705}=10^{-5}$
(a,c) and
![]() $\unicode[STIX]{x1D705}=10^{3}$
(b,d). The dashed red lines indicate 5 % deviation from the values of mean and standard deviation for the entire pool.
$\unicode[STIX]{x1D705}=10^{3}$
(b,d). The dashed red lines indicate 5 % deviation from the values of mean and standard deviation for the entire pool.