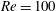1 Introduction
The flow past a circular cylinder is one of the most famous and well-studied problems in fluid mechanics. At a Reynolds number above a certain critical value, the steady base flow becomes unstable through a supercritical Hopf bifurcation, and the saturation of this primary instability leads to the formation of a time-periodic Kármán vortex street that propagates in the wake of the cylinder (Jackson Reference Jackson1987; Provansal, Mathis & Boyer Reference Provansal, Mathis and Boyer1987). An infinite double row of staggered point vortices was first proposed by von Kármán (Reference von Kármán1911, Reference von Kármán1912) as a simplified model for this periodic and two-dimensional flow. However, he found this system to be linearly unstable to infinitesimal perturbations of the positions of the vortices, except for one specific value of the aspect ratio between transverse to longitudinal spacing of the vortices. This result, implying secondary instability of the flow past a cylinder, seemed in contradiction with common observations of persistent vortex streets, which motivated other authors to consider more sophisticated models in the hope that these might produce a finite range of stable aspect ratios.
A first attempt was done by Rosenhead (Reference Rosenhead1929), who extended Kármán’s model to include the effect of confining walls. The instability behaviour of the street nonetheless remained the same and stability was only observed at a specific value of the aspect ratio for all but the highest degrees of confinement. Several authors then considered a generalization of Kármán’s point vortex model to vortices of finite size. In this context, Saffman & Schatzman (Reference Saffman and Schatzman1982b ) investigated the growth rate of the pairing instability, a disturbance of wavelength twice the vortex spacing that was the most unstable mode in Kármán’s model. Although they found stabilization of the pairing instability for a finite range of aspect ratios around Kármán’s specific value, Kida (Reference Kida1982) soon discovered that this perturbation was no longer the most unstable one in the case of finite-size vortices. Errors in his calculations, however, led him to the false conclusion that finite size still induced a finite range of stable aspect ratios. This claim was quickly rectified by Meiron, Saffman & Schatzman (Reference Meiron, Saffman and Schatzman1984), who proved that the finite-size vortex street is always unstable except for a specific value of its aspect ratio, similarly to Kármán’s and Rosenhead’s point vortex models. Jiménez (Reference Jiménez1987) (see also MacKay Reference Mackay1987) eventually found that, as a consequence of the Hamiltonian structure and the back-to-fore symmetry of Kármán’s street of point vortices, instability for all but a specific value of the parameters is a generic feature of all these inviscid models. In practice, this general result settled the issue of the inviscid stability of the Kármán vortex street, while questioning the relevance of these inviscid models and leaving open the question about the reason for the permanence of the observed vortex streets. In the words of Jiménez (Reference Jiménez1988), ‘the persistence of a natural vortex street is most probably due to viscous effects, or to the differences between the spatial development of natural wakes and the temporal evolution model…’.
The above classical stability analyses consider the temporal growth of perturbations of infinite spatial extent, and therefore predict instability of the aforementioned inviscid models regardless of the advection velocity or spatial development of the actual vortex street. Subsequent years, however, have seen important developments in the study of spatially developing unstable flows from a spatio-temporal perspective, wherein one instead analyses the linear impulse response of the system in a specific reference frame, usually that of the laboratory. A localized initial perturbation generates a growing wave packet that might either contaminate the whole domain, in which case the flow is termed absolutely unstable, or be convected away from its initial location due to advection by the external flow, corresponding to a convectively unstable flow (see the review by Huerre & Monkewitz Reference Huerre and Monkewitz1990). This time, the velocity at which the system is advected downstream plays a crucial role in the absolute or convective behaviour of the instability, which will in turn affect the global dynamical behaviour of the system. An absolutely unstable flow will eventually lose its initial structure due to the temporal growth of the instability over the whole domain. By contrast, disturbances in a convectively unstable flow are unable to reach the upstream source of the flow and only experience downstream spatial growth, in such a way that the flow will retain its initial structure up to a certain downstream location.
These concepts first became popular in the analysis of the primary instability of open shear flows, and the Kármán vortex street was notably shown to arise from the absolute primary instability of the steady wake flow (Monkewitz Reference Monkewitz1988; Pier Reference Pier2002; Barkley Reference Barkley2006). Later, Brancher & Chomaz (Reference Brancher and Chomaz1997) successfully applied these ideas to the secondary instability of spatially periodic flows resulting from the saturation of an unstable primary mode. In particular, they showed that the single row of vortices induced by a mixing layer, while being subject to a secondary instability, becomes convectively unstable above a critical value of its advection velocity. In this case, the regular pattern of vortices is expected to persist over a certain downstream distance, until disturbances have grown sufficiently, and lead to pairing of the vortices further downstream.
We propose to apply the same spatio-temporal ideas to the secondary instability of the Kármán vortex street, accounting for its natural advection at a certain velocity due to the external flow. Returning to Kármán’s point vortices, we perform this spatio-temporal instability analysis on Rosenhead’s model so as to account for confining walls. Recent work has indeed shown the importance of confinement for the transition from convective to absolute instability of wakes and mixing layers (Juniper Reference Juniper2006; Healey Reference Healey2009). The unconfined scenario is still included as a limiting case of the model. We will see that the secondary instability turns out to be of convective nature in a wide range of parameters, reconciling the longstanding conflict between temporal instability of the inviscid models and experimental evidence of the persistence of the Kármán vortex street. Our results are also in agreement with the work of Henderson & Barkley (Reference Henderson and Barkley1996), who studied the secondary instability in the wake of a cylinder using Floquet theory and showed that the real time-periodic flow is stable.
The paper is structured as follows. The model and its dispersion relation are presented in § 2, together with known temporal instability results. A numerical method for the time evolution of the system is then introduced in § 3, and allows for the obtention in § 4 of the critical advection velocity of the vortices above which the model becomes convectively unstable. Finally, in § 5 this critical velocity is compared to the advection velocity of an actual vortex street observed behind a cylinder in a direct numerical simulation, leading to the determination of the absolutely or convectively unstable nature of the vortex street. Conclusions follow in § 6.
2 Problem formulation and temporal stability analysis
2.1 Equations of motion
We consider the simplified model for the confined Kármán vortex street studied by Rosenhead (Reference Rosenhead1929). As shown in figure 1, this system consists of an infinite asymmetric double row of point vortices, symmetrically enclosed between two horizontal confining walls. Vortices in one row are situated opposite of the midpoint between two successive vortices in the other row. The distance between two consecutive vortices in the same row is
![]() $a$
and that between the two rows is
$a$
and that between the two rows is
![]() $h$
. The walls are separated by a distance
$h$
. The walls are separated by a distance
![]() $d$
. All the vortices in the lower row have the same circulation
$d$
. All the vortices in the lower row have the same circulation
![]() ${\it\Gamma}$
and those in the upper row the opposite circulation
${\it\Gamma}$
and those in the upper row the opposite circulation
![]() $-{\it\Gamma}$
.
$-{\it\Gamma}$
.

Figure 1. Confined Kármán vortex street.
The confinement is taken into account by assigning to each vortex in the lower and upper rows an infinite vertical series of image vortices above and below the walls, at positions tied to that of the corresponding physical vortex inside the channel. This results in two doubly infinite arrays of vortices. Lower-row vortices are situated at coordinates
![]() $(ma,nd-(-1)^{n}h/2)$
and have strength
$(ma,nd-(-1)^{n}h/2)$
and have strength
![]() $(-1)^{n}{\it\Gamma}$
, while upper-row vortices are situated at coordinates
$(-1)^{n}{\it\Gamma}$
, while upper-row vortices are situated at coordinates
![]() $(ma+a/2,nd+(-1)^{n}h/2)$
and have strength
$(ma+a/2,nd+(-1)^{n}h/2)$
and have strength
![]() $-(-1)^{n}{\it\Gamma}$
, where
$-(-1)^{n}{\it\Gamma}$
, where
![]() $m,n\in \mathbb{Z}$
and
$m,n\in \mathbb{Z}$
and
![]() $n=0$
corresponds to the physical vortices. The geometry of the system is entirely specified by the aspect ratio
$n=0$
corresponds to the physical vortices. The geometry of the system is entirely specified by the aspect ratio
![]() $p=h/a$
of the vortex street and its confinement ratio
$p=h/a$
of the vortex street and its confinement ratio
![]() $q=d/a$
, and we require
$q=d/a$
, and we require
![]() $p<q$
in order for the model to remain physical.
$p<q$
in order for the model to remain physical.
This array of vortices corresponds to an equilibrium configuration that moves horizontally with a self-induced velocity
![]() $v_{0}$
given by Rosenhead (Reference Rosenhead1929)
$v_{0}$
given by Rosenhead (Reference Rosenhead1929)
 $$\begin{eqnarray}\displaystyle v_{0} & = & \displaystyle \frac{{\it\Gamma}}{4d}\left[\tan \left(\frac{{\rm\pi}p}{2q}\right)+\mathop{\sum }_{m=-\infty }^{\infty }\!\!\!\displaystyle \vphantom{\sum }^{\prime }\;\frac{\sin ({\rm\pi}p/q)}{\cosh ({\rm\pi}m/q)+\cos ({\rm\pi}p/q)}\right.\nonumber\\ \displaystyle & & \displaystyle \left.-\,\mathop{\sum }_{m=-\infty }^{\infty }\frac{\sin ({\rm\pi}p/q)}{\cosh ({\rm\pi}(m-1/2)/q)-\cos ({\rm\pi}p/q)}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle v_{0} & = & \displaystyle \frac{{\it\Gamma}}{4d}\left[\tan \left(\frac{{\rm\pi}p}{2q}\right)+\mathop{\sum }_{m=-\infty }^{\infty }\!\!\!\displaystyle \vphantom{\sum }^{\prime }\;\frac{\sin ({\rm\pi}p/q)}{\cosh ({\rm\pi}m/q)+\cos ({\rm\pi}p/q)}\right.\nonumber\\ \displaystyle & & \displaystyle \left.-\,\mathop{\sum }_{m=-\infty }^{\infty }\frac{\sin ({\rm\pi}p/q)}{\cosh ({\rm\pi}(m-1/2)/q)-\cos ({\rm\pi}p/q)}\right],\end{eqnarray}$$
where the prime on the summation sign means that
![]() $m=0$
is excluded. This equilibrium configuration forms the base flow of our subsequent stability analysis. In figure 2, we plot
$m=0$
is excluded. This equilibrium configuration forms the base flow of our subsequent stability analysis. In figure 2, we plot
![]() $v_{0}$
as a function of the confinement ratio
$v_{0}$
as a function of the confinement ratio
![]() $q$
, for different values of the aspect ratio
$q$
, for different values of the aspect ratio
![]() $p$
. As the confinement increases, the initially negative self-induced velocity increases and eventually becomes positive, as the physical vortices become more affected by their closest images than by the physical vortices of the opposite row.
$p$
. As the confinement increases, the initially negative self-induced velocity increases and eventually becomes positive, as the physical vortices become more affected by their closest images than by the physical vortices of the opposite row.

Figure 2. Non-dimensional self-induced velocity
![]() $2{\rm\pi}av_{0}/{\it\Gamma}$
of the vortex street versus confinement ratio
$2{\rm\pi}av_{0}/{\it\Gamma}$
of the vortex street versus confinement ratio
![]() $q$
, for different values of the aspect ratio
$q$
, for different values of the aspect ratio
![]() $p$
. As
$p$
. As
![]() $q$
increases, the self-induced velocity tends to its unconfined value of
$q$
increases, the self-induced velocity tends to its unconfined value of
![]() $-0.9557$
(
$-0.9557$
(
![]() $p=0.10$
),
$p=0.10$
),
![]() $-2.0602$
(
$-2.0602$
(
![]() $p=0.25$
) and
$p=0.25$
) and
![]() $-2.6708$
(
$-2.6708$
(
![]() $p=0.40$
).
$p=0.40$
).
We now place ourselves in a frame of reference moving with the vortices at the self-induced velocity
![]() $v_{0}$
. Applying a perturbation
$v_{0}$
. Applying a perturbation
![]() $(x_{m},y_{m})$
and
$(x_{m},y_{m})$
and
![]() $(x_{m}^{\prime },y_{m}^{\prime })$
to the positions of the lower- and upper-row physical vortices, respectively, the coordinates of the lower-row vortices become
$(x_{m}^{\prime },y_{m}^{\prime })$
to the positions of the lower- and upper-row physical vortices, respectively, the coordinates of the lower-row vortices become
![]() $(ma+x_{m},nd+(-1)^{n}(-h/2+y_{m}))$
, while those of the upper row become
$(ma+x_{m},nd+(-1)^{n}(-h/2+y_{m}))$
, while those of the upper row become
![]() $(ma+a/2+x_{m}^{\prime },nd+(-1)^{n}(h/2+y_{m}^{\prime }))$
. The equations of motion of the
$(ma+a/2+x_{m}^{\prime },nd+(-1)^{n}(h/2+y_{m}^{\prime }))$
. The equations of motion of the
![]() $m=0$
physical vortex of the lower row are
$m=0$
physical vortex of the lower row are
 $$\begin{eqnarray}\displaystyle \frac{\text{d}x_{0}}{\text{d}t}+v_{0} & = & \displaystyle -\frac{{\it\Gamma}}{2{\rm\pi}}\mathop{\sum }_{m=-\infty }^{\infty }\mathop{\sum }_{n=-\infty }^{\infty }\!\!\!\displaystyle \vphantom{\sum }^{\prime \prime }\;(-1)^{n}\frac{y_{0}-nd-(1-(-1)^{n})h/2-(-1)^{n}y_{m}}{r_{m,n}^{2}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{{\it\Gamma}}{2{\rm\pi}}\mathop{\sum }_{m=-\infty }^{\infty }\mathop{\sum }_{n=-\infty }^{\infty }(-1)^{n}\frac{y_{0}-nd-(1+(-1)^{n})h/2-(-1)^{n}y_{m}^{\prime }}{r_{m,n}^{\prime 2}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\text{d}x_{0}}{\text{d}t}+v_{0} & = & \displaystyle -\frac{{\it\Gamma}}{2{\rm\pi}}\mathop{\sum }_{m=-\infty }^{\infty }\mathop{\sum }_{n=-\infty }^{\infty }\!\!\!\displaystyle \vphantom{\sum }^{\prime \prime }\;(-1)^{n}\frac{y_{0}-nd-(1-(-1)^{n})h/2-(-1)^{n}y_{m}}{r_{m,n}^{2}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{{\it\Gamma}}{2{\rm\pi}}\mathop{\sum }_{m=-\infty }^{\infty }\mathop{\sum }_{n=-\infty }^{\infty }(-1)^{n}\frac{y_{0}-nd-(1+(-1)^{n})h/2-(-1)^{n}y_{m}^{\prime }}{r_{m,n}^{\prime 2}},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \frac{1}{{\it\omega}_{0}}\frac{\text{d}x_{0}}{\text{d}t} & = & \displaystyle -\mathop{\sum }_{m=-\infty }^{\infty }\!\!\!\displaystyle \vphantom{\sum }^{\prime }\;\mathop{\sum }_{n=-\infty }^{\infty }[(-1)^{n}A_{mn}^{-}x_{m}+B_{mn}^{-}(y_{m}-(-1)^{n}y_{0})]-\mathop{\sum }_{n=-\infty }^{\infty }C_{n}y_{0}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{m=-\infty }^{\infty }\mathop{\sum }_{n=-\infty }^{\infty }[(-1)^{n}A_{m+1/2,n}^{+}x_{m}^{\prime }+B_{m+1/2,n}^{+}(y_{m}^{\prime }-(-1)^{n}y_{0})],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{1}{{\it\omega}_{0}}\frac{\text{d}x_{0}}{\text{d}t} & = & \displaystyle -\mathop{\sum }_{m=-\infty }^{\infty }\!\!\!\displaystyle \vphantom{\sum }^{\prime }\;\mathop{\sum }_{n=-\infty }^{\infty }[(-1)^{n}A_{mn}^{-}x_{m}+B_{mn}^{-}(y_{m}-(-1)^{n}y_{0})]-\mathop{\sum }_{n=-\infty }^{\infty }C_{n}y_{0}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{m=-\infty }^{\infty }\mathop{\sum }_{n=-\infty }^{\infty }[(-1)^{n}A_{m+1/2,n}^{+}x_{m}^{\prime }+B_{m+1/2,n}^{+}(y_{m}^{\prime }-(-1)^{n}y_{0})],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \frac{1}{{\it\omega}_{0}}\frac{\text{d}y_{0}}{\text{d}t} & = & \displaystyle -\mathop{\sum }_{m=-\infty }^{\infty }\!\!\!\displaystyle \vphantom{\sum }^{\prime }\;\mathop{\sum }_{n=-\infty }^{\infty }[(-1)^{n}B_{mn}^{-}(x_{m}-x_{0})-A_{mn}^{-}y_{m}]\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{m=-\infty }^{\infty }\mathop{\sum }_{n=-\infty }^{\infty }[(-1)^{n}B_{m+1/2,n}^{+}(x_{m}^{\prime }-x_{0})-A_{m+1/2,n}^{+}y_{m}^{\prime }],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{1}{{\it\omega}_{0}}\frac{\text{d}y_{0}}{\text{d}t} & = & \displaystyle -\mathop{\sum }_{m=-\infty }^{\infty }\!\!\!\displaystyle \vphantom{\sum }^{\prime }\;\mathop{\sum }_{n=-\infty }^{\infty }[(-1)^{n}B_{mn}^{-}(x_{m}-x_{0})-A_{mn}^{-}y_{m}]\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{m=-\infty }^{\infty }\mathop{\sum }_{n=-\infty }^{\infty }[(-1)^{n}B_{m+1/2,n}^{+}(x_{m}^{\prime }-x_{0})-A_{m+1/2,n}^{+}y_{m}^{\prime }],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \frac{2q^{2}}{{\rm\pi}^{2}{\it\omega}_{0}}\frac{\text{d}x_{0}}{\text{d}t} & = & \displaystyle -\mathop{\sum }_{m=-\infty }^{\infty }\!\!\!\displaystyle \vphantom{\sum }^{\prime }\;[D_{m}^{+}x_{m}+E_{m}^{+}(y_{m}+y_{0})-F_{m}^{-}(y_{m}-y_{0})]-\sec ^{2}\left(\frac{{\rm\pi}p}{2q}\right)y_{0}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{m=-\infty }^{\infty }[D_{m+1/2}^{-}x_{m}^{\prime }-E_{m+1/2}^{-}(y_{m}^{\prime }-y_{0})+F_{m+1/2}^{+}(y_{m}^{\prime }+y_{0})],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{2q^{2}}{{\rm\pi}^{2}{\it\omega}_{0}}\frac{\text{d}x_{0}}{\text{d}t} & = & \displaystyle -\mathop{\sum }_{m=-\infty }^{\infty }\!\!\!\displaystyle \vphantom{\sum }^{\prime }\;[D_{m}^{+}x_{m}+E_{m}^{+}(y_{m}+y_{0})-F_{m}^{-}(y_{m}-y_{0})]-\sec ^{2}\left(\frac{{\rm\pi}p}{2q}\right)y_{0}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{m=-\infty }^{\infty }[D_{m+1/2}^{-}x_{m}^{\prime }-E_{m+1/2}^{-}(y_{m}^{\prime }-y_{0})+F_{m+1/2}^{+}(y_{m}^{\prime }+y_{0})],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \frac{2q^{2}}{{\rm\pi}^{2}{\it\omega}_{0}}\frac{\text{d}y_{0}}{\text{d}t} & = & \displaystyle +\mathop{\sum }_{m=-\infty }^{\infty }\!\!\!\displaystyle \vphantom{\sum }^{\prime }\;[(E_{m}^{+}+F_{m}^{-})(x_{m}-x_{0})-D_{m}^{+}y_{m}]\nonumber\\ \displaystyle & & \displaystyle -\,\mathop{\sum }_{m=-\infty }^{\infty }[(E_{m+1/2}^{-}+F_{m+1/2}^{+})(x_{m}^{\prime }-x_{0})+D_{m+1/2}^{-}y_{m}^{\prime }],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{2q^{2}}{{\rm\pi}^{2}{\it\omega}_{0}}\frac{\text{d}y_{0}}{\text{d}t} & = & \displaystyle +\mathop{\sum }_{m=-\infty }^{\infty }\!\!\!\displaystyle \vphantom{\sum }^{\prime }\;[(E_{m}^{+}+F_{m}^{-})(x_{m}-x_{0})-D_{m}^{+}y_{m}]\nonumber\\ \displaystyle & & \displaystyle -\,\mathop{\sum }_{m=-\infty }^{\infty }[(E_{m+1/2}^{-}+F_{m+1/2}^{+})(x_{m}^{\prime }-x_{0})+D_{m+1/2}^{-}y_{m}^{\prime }],\end{eqnarray}$$
2.2 Dispersion relation
We hereafter non-dimensionalize all quantities with the characteristic length
![]() $a$
and time
$a$
and time
![]() $1/{\it\omega}_{0}=2{\rm\pi}a^{2}/{\it\Gamma}$
. Let us now expand the perturbation into normal modes of the type
$1/{\it\omega}_{0}=2{\rm\pi}a^{2}/{\it\Gamma}$
. Let us now expand the perturbation into normal modes of the type
 $$\begin{eqnarray}\left[\begin{array}{@{}cccc@{}}M+\text{i}{\it\omega} & N & O & P\\ Q & M+\text{i}{\it\omega} & R & -O\\ O & -P & M+\text{i}{\it\omega} & -N\\ -R & -O & -Q & M+\text{i}{\it\omega}\end{array}\right]\left[\begin{array}{@{}c@{}}{\it\alpha}\\ {\it\beta}\\ {\it\alpha}^{\prime }\\ {\it\beta}^{\prime }\end{array}\right]=\left[\begin{array}{@{}c@{}}0\\ 0\\ 0\\ 0\end{array}\right],\end{eqnarray}$$
$$\begin{eqnarray}\left[\begin{array}{@{}cccc@{}}M+\text{i}{\it\omega} & N & O & P\\ Q & M+\text{i}{\it\omega} & R & -O\\ O & -P & M+\text{i}{\it\omega} & -N\\ -R & -O & -Q & M+\text{i}{\it\omega}\end{array}\right]\left[\begin{array}{@{}c@{}}{\it\alpha}\\ {\it\beta}\\ {\it\alpha}^{\prime }\\ {\it\beta}^{\prime }\end{array}\right]=\left[\begin{array}{@{}c@{}}0\\ 0\\ 0\\ 0\end{array}\right],\end{eqnarray}$$
where the coefficients
![]() $M$
,
$M$
,
![]() $N$
,
$N$
,
![]() $O$
,
$O$
,
![]() $P$
,
$P$
,
![]() $Q$
and
$Q$
and
![]() $R$
, defined in appendix A, depend on the perturbation wavenumber
$R$
, defined in appendix A, depend on the perturbation wavenumber
![]() $k$
, the aspect ratio
$k$
, the aspect ratio
![]() $p$
and the confinement ratio
$p$
and the confinement ratio
![]() $q$
. There are two possible modes of disturbance: a symmetric mode with
$q$
. There are two possible modes of disturbance: a symmetric mode with
![]() ${\it\alpha}={\it\alpha}^{\prime }$
,
${\it\alpha}={\it\alpha}^{\prime }$
,
![]() ${\it\beta}=-{\it\beta}^{\prime }$
, and an antisymmetric mode with
${\it\beta}=-{\it\beta}^{\prime }$
, and an antisymmetric mode with
![]() ${\it\alpha}=-{\it\alpha}^{\prime }$
,
${\it\alpha}=-{\it\alpha}^{\prime }$
,
![]() ${\it\beta}={\it\beta}^{\prime }$
. Grouping the two modes together, we obtain
${\it\beta}={\it\beta}^{\prime }$
. Grouping the two modes together, we obtain
where the upper and lower signs correspond to the symmetric and antisymmetric modes, respectively. Finally, setting the determinant of the above matrix to zero yields the dispersion relation
where
![]() $s=\pm 1$
give two solution branches for each mode. Equation (2.11) is a corrected version of the dispersion relation given by Rosenhead (Reference Rosenhead1929), who incorrectly fixed the spatial phase by imposing modal solutions with a cosine spatial dependence. This error was also noted by Jiménez (Reference Jiménez1987), but he did not provide the correct dispersion relation since he was only interested in the stability from a temporal perspective, which turns out to be unaffected by this issue. To our knowledge, the correct dispersion relation for the confined Kármán vortex street is given in (2.11) for the first time.
$s=\pm 1$
give two solution branches for each mode. Equation (2.11) is a corrected version of the dispersion relation given by Rosenhead (Reference Rosenhead1929), who incorrectly fixed the spatial phase by imposing modal solutions with a cosine spatial dependence. This error was also noted by Jiménez (Reference Jiménez1987), but he did not provide the correct dispersion relation since he was only interested in the stability from a temporal perspective, which turns out to be unaffected by this issue. To our knowledge, the correct dispersion relation for the confined Kármán vortex street is given in (2.11) for the first time.
2.3 Temporal stability analysis
For the temporal stability of this discrete system,
![]() $k$
is assigned a real value between 0 and
$k$
is assigned a real value between 0 and
![]() $2{\rm\pi}$
, while
$2{\rm\pi}$
, while
![]() ${\it\omega}$
is given by the dispersion relation (2.11) and may be complex. The imaginary part of
${\it\omega}$
is given by the dispersion relation (2.11) and may be complex. The imaginary part of
![]() ${\it\omega}$
gives the growth rate of the perturbation, and needs to be zero for all values of
${\it\omega}$
gives the growth rate of the perturbation, and needs to be zero for all values of
![]() $k$
for the system to be temporally stable to infinitesimal disturbances. We restrict ourselves to values of
$k$
for the system to be temporally stable to infinitesimal disturbances. We restrict ourselves to values of
![]() $k$
between 0 and
$k$
between 0 and
![]() ${\rm\pi}$
, since symmetric disturbances of wavenumber
${\rm\pi}$
, since symmetric disturbances of wavenumber
![]() $2{\rm\pi}-k$
are equivalent to the complex conjugate of antisymmetric disturbances of wavenumber
$2{\rm\pi}-k$
are equivalent to the complex conjugate of antisymmetric disturbances of wavenumber
![]() $k$
and vice-versa (as acknowledged in Meiron et al. (Reference Meiron, Saffman and Schatzman1984), it was the oversight that the symmetry about
$k$
and vice-versa (as acknowledged in Meiron et al. (Reference Meiron, Saffman and Schatzman1984), it was the oversight that the symmetry about
![]() $k={\rm\pi}$
relates to different modes that led (Saffman & Schatzman Reference Saffman and Schatzman1982b
) to expect the most unstable perturbation for
$k={\rm\pi}$
relates to different modes that led (Saffman & Schatzman Reference Saffman and Schatzman1982b
) to expect the most unstable perturbation for
![]() $k={\rm\pi}$
). Note that the conservative nature of the system implies that the two solution branches pertaining to each mode will be either real or complex conjugate numbers.
$k={\rm\pi}$
). Note that the conservative nature of the system implies that the two solution branches pertaining to each mode will be either real or complex conjugate numbers.

Figure 3. Temporal dispersion relation. Growth rate
![]() ${\it\omega}_{i}$
of the symmetric (continuous line) and antisymmetric (dotted line with circles) modes versus wavenumber
${\it\omega}_{i}$
of the symmetric (continuous line) and antisymmetric (dotted line with circles) modes versus wavenumber
![]() $k$
, for different aspect ratios
$k$
, for different aspect ratios
![]() $p$
and (a)
$p$
and (a)
![]() $q=20$
, i.e. almost no confinement, and (b)
$q=20$
, i.e. almost no confinement, and (b)
![]() $q=1.2$
, i.e. strong confinement. The growth rate of antisymmetric perturbations of wavenumber
$q=1.2$
, i.e. strong confinement. The growth rate of antisymmetric perturbations of wavenumber
![]() $2{\rm\pi}-k$
is equivalent to that of symmetric perturbations of wavenumber
$2{\rm\pi}-k$
is equivalent to that of symmetric perturbations of wavenumber
![]() $k$
and vice-versa.
$k$
and vice-versa.
Figure 3 compares the growth rate
![]() ${\it\omega}_{i}$
of the unstable branch of the symmetric (continuous lines) and antisymmetric (dotted lines with circles) modes versus the wavenumber
${\it\omega}_{i}$
of the unstable branch of the symmetric (continuous lines) and antisymmetric (dotted lines with circles) modes versus the wavenumber
![]() $k$
, for different aspect ratios
$k$
, for different aspect ratios
![]() $p$
and two confinement ratios
$p$
and two confinement ratios
![]() $q$
. When the confinement is very weak, as shown in figure 3(a) for
$q$
. When the confinement is very weak, as shown in figure 3(a) for
![]() $q=20$
, the two modes have the same growth rate that reaches a maximum at
$q=20$
, the two modes have the same growth rate that reaches a maximum at
![]() $k={\rm\pi}$
, which is no longer the case under strong confinement, as seen in figure 3(b) for
$k={\rm\pi}$
, which is no longer the case under strong confinement, as seen in figure 3(b) for
![]() $q=1.2$
. Comparing figures 3(a) and (b) shows that both the aspect and confinement ratios have an effect on the range of unstable wavenumbers and the amplitude of the growth rate. In figure 4, we plot the isolines of the growth rate of the most unstable wavenumber versus the aspect and confinement ratios. The vortex street is temporally stable when this maximum growth rate is zero, which only happens at a very specific value of the aspect ratio unless the confinement is extremely strong. Interestingly, nearly unadvected vortex streets falling in the stable region of strong confinement have been observed in recent experiments of a moving stripe dragging the surface of shallow water in a long tank (Boniface Reference Boniface2014). When the confinement decreases, the range of stable aspect ratios reduces to a specific value that approaches the limiting value
$q=1.2$
. Comparing figures 3(a) and (b) shows that both the aspect and confinement ratios have an effect on the range of unstable wavenumbers and the amplitude of the growth rate. In figure 4, we plot the isolines of the growth rate of the most unstable wavenumber versus the aspect and confinement ratios. The vortex street is temporally stable when this maximum growth rate is zero, which only happens at a very specific value of the aspect ratio unless the confinement is extremely strong. Interestingly, nearly unadvected vortex streets falling in the stable region of strong confinement have been observed in recent experiments of a moving stripe dragging the surface of shallow water in a long tank (Boniface Reference Boniface2014). When the confinement decreases, the range of stable aspect ratios reduces to a specific value that approaches the limiting value
![]() $p_{0}=1/{\rm\pi}\sinh ^{-1}1\simeq 0.281$
found by von Kármán (Reference von Kármán1912) in the unconfined case.
$p_{0}=1/{\rm\pi}\sinh ^{-1}1\simeq 0.281$
found by von Kármán (Reference von Kármán1912) in the unconfined case.

Figure 4. Temporal dispersion relation. Isolines of the growth rate of the most unstable wavenumber versus aspect ratio
![]() $p$
and confinement ratio
$p$
and confinement ratio
![]() $q$
. The black lines indicate the range of parameter values under which the spatio-temporal characteristics of the impulse response of the vortex street is evaluated in figures 11 and 12.
$q$
. The black lines indicate the range of parameter values under which the spatio-temporal characteristics of the impulse response of the vortex street is evaluated in figures 11 and 12.
3 Numerical method
3.1 Numerical integration of the governing equations
We consider a finite vortex street consisting of
![]() $M$
physical vortices and we compute its temporal evolution through direct time integration of the equations of motion. However, the model contains an infinite number of vortices in the streamwise direction, represented by the infinite series in the equations of motion. We thus introduce additional virtual vortices situated to the left and right of the
$M$
physical vortices and we compute its temporal evolution through direct time integration of the equations of motion. However, the model contains an infinite number of vortices in the streamwise direction, represented by the infinite series in the equations of motion. We thus introduce additional virtual vortices situated to the left and right of the
![]() $M$
physical vortices and slaved to them in such a way that the displacement of the virtual vortex of index
$M$
physical vortices and slaved to them in such a way that the displacement of the virtual vortex of index
![]() $m^{\prime }$
is equal to that of the
$m^{\prime }$
is equal to that of the
![]() $m$
th physical vortex, where
$m$
th physical vortex, where
![]() $m=(m^{\prime }\,\text{mod}\,M)\in [0,M-1]$
. The linearized perturbation equations (2.6) are then applied to each of the
$m=(m^{\prime }\,\text{mod}\,M)\in [0,M-1]$
. The linearized perturbation equations (2.6) are then applied to each of the
![]() $M$
physical vortices, taking into account the velocities induced by the virtual vortices, and are advanced in time with an Adams–Bashforth scheme. This procedure is implemented in MATLAB with a time step
$M$
physical vortices, taking into account the velocities induced by the virtual vortices, and are advanced in time with an Adams–Bashforth scheme. This procedure is implemented in MATLAB with a time step
![]() ${\rm\Delta}t=0.005$
and
${\rm\Delta}t=0.005$
and
![]() $M=402$
physical vortices. Since the amplitude of the velocities induced by the virtual vortices decreases as
$M=402$
physical vortices. Since the amplitude of the velocities induced by the virtual vortices decreases as
![]() $1/m^{2}$
with their index
$1/m^{2}$
with their index
![]() $m$
, we found that including
$m$
, we found that including
![]() $10M$
virtual vortices is largely sufficient in order to reduce the error to a negligible value. In the following, lengths and time are non-dimensionalized with
$10M$
virtual vortices is largely sufficient in order to reduce the error to a negligible value. In the following, lengths and time are non-dimensionalized with
![]() $a$
and
$a$
and
![]() $1/{\it\omega}_{0}=2{\rm\pi}a^{2}/{\it\Gamma}$
, respectively.
$1/{\it\omega}_{0}=2{\rm\pi}a^{2}/{\it\Gamma}$
, respectively.
3.2 Validation
In order to validate the numerical method, we calculate the response of the vortex street to a random initial perturbation spanning the entire wavenumber spectrum, from which we can extract the temporal growth rate of each real wavenumber
![]() $k$
. Recall however that there are two modes of disturbance, symmetric and antisymmetric, with two branches each. Therefore, for every wavenumber
$k$
. Recall however that there are two modes of disturbance, symmetric and antisymmetric, with two branches each. Therefore, for every wavenumber
![]() $k$
we construct from the solution a state vector consisting of the Fourier transforms of the horizontal and vertical displacements in both rows and we rely on a Krylov subspace method of dimension
$k$
we construct from the solution a state vector consisting of the Fourier transforms of the horizontal and vertical displacements in both rows and we rely on a Krylov subspace method of dimension
![]() $4$
with Gram–Schmidt orthogonalization to isolate the temporal growth rate of each unstable mode. In figure 5, we plot in solid line the growth rate
$4$
with Gram–Schmidt orthogonalization to isolate the temporal growth rate of each unstable mode. In figure 5, we plot in solid line the growth rate
![]() ${\it\omega}_{i}$
of the two leading eigenmodes, obtained from the calculated response at times 18, 18.1, 18.2, 18.3 and 18.4 of the Kármán street with parameters
${\it\omega}_{i}$
of the two leading eigenmodes, obtained from the calculated response at times 18, 18.1, 18.2, 18.3 and 18.4 of the Kármán street with parameters
![]() $q=1.2$
and
$q=1.2$
and
![]() $p=0.2$
. The black and grey lines correspond respectively to the symmetric and antisymmetric modes, and both agree extremely well with the analytical dispersion relation (2.11) shown in dotted lines with circles.
$p=0.2$
. The black and grey lines correspond respectively to the symmetric and antisymmetric modes, and both agree extremely well with the analytical dispersion relation (2.11) shown in dotted lines with circles.

Figure 5. Comparison of the temporal dispersion relation extracted from the simulation with its analytical counterpart. The growth rate of the symmetric (black) and antisymmetric (grey) modes are plotted against the wavenumber, for parameters
![]() $q=1.2$
and
$q=1.2$
and
![]() $p=0.2$
.
$p=0.2$
.
4 Spatio-temporal results
The absolute/convective nature of the instability associated with the vortex street is determined by the spatio-temporal behaviour of the growing wave packet induced by a localized initial perturbation. In a similar fashion as done in Brancher & Chomaz (Reference Brancher and Chomaz1997) and Delbende, Chomaz & Huerre (Reference Delbende, Chomaz and Huerre1998), we carry out a numerical simulation of the impulse response of the vortex street and we directly retrieve the asymptotic properties of the resulting wave packet. The total time of the simulation is about 40 and is chosen such that the asymptotic regime is reached while ensuring that the wave packet remains contained within the elementary vortices.
The numerical simulation is carried out in the frame of reference moving with the vortices, and is initialized with a localized perturbation created by a small vertical displacement of the centre vortex in both rows. In order to visualize the growth of the perturbation, the displacements from the two rows are first assembled together, resulting in vectors
![]() $\bar{x}_{m}$
and
$\bar{x}_{m}$
and
![]() $\bar{y}_{m}$
for the horizontal and vertical displacements respectively, where even (odd) indices indicate lower (upper) row vortices. The envelope of this composed signal is then computed from its analytic representation, i.e. by setting all negative-wavenumber modes of its Fourier transforms to zero. Finally, the Fourier components corresponding to temporally stable wavenumbers are also set to zero and the reconstructed real amplitude of the perturbation is defined as
$\bar{y}_{m}$
for the horizontal and vertical displacements respectively, where even (odd) indices indicate lower (upper) row vortices. The envelope of this composed signal is then computed from its analytic representation, i.e. by setting all negative-wavenumber modes of its Fourier transforms to zero. Finally, the Fourier components corresponding to temporally stable wavenumbers are also set to zero and the reconstructed real amplitude of the perturbation is defined as
where
![]() $m=\text{round}(2x)$
and
$m=\text{round}(2x)$
and
![]() $|\cdot |$
denotes the complex modulus. The growth rate observed along spatio-temporal rays
$|\cdot |$
denotes the complex modulus. The growth rate observed along spatio-temporal rays
![]() $x/t=v_{g}$
radiating from the initial location of the perturbation can be evaluated from values of the amplitude at two distinct time instants
$x/t=v_{g}$
radiating from the initial location of the perturbation can be evaluated from values of the amplitude at two distinct time instants
![]() $t_{1}$
and
$t_{1}$
and
![]() $t_{2}$
via the following expression
$t_{2}$
via the following expression
The results in §§ 4.1 and 4.2 will be presented in the same frame of reference in which the simulation is carried out, i.e. that moving with the vortices.
4.1 Unconfined case
4.1.1 Results from the numerical method
Numerical simulations with a confinement ratio
![]() $q=100$
that approaches the unconfined limiting case are first considered. The growth of the impulse response wave packet for
$q=100$
that approaches the unconfined limiting case are first considered. The growth of the impulse response wave packet for
![]() $p=0.25$
is illustrated in figure 6(a) through the time series of the amplitude
$p=0.25$
is illustrated in figure 6(a) through the time series of the amplitude
![]() $A(v_{g}t,t)$
observed along each spatio-temporal ray
$A(v_{g}t,t)$
observed along each spatio-temporal ray
![]() $x/t=v_{g}$
. The corresponding growth rate
$x/t=v_{g}$
. The corresponding growth rate
![]() ${\it\sigma}(v_{g})$
obtained from (4.2) with the amplitude at times
${\it\sigma}(v_{g})$
obtained from (4.2) with the amplitude at times
![]() $t_{1}=18$
and
$t_{1}=18$
and
![]() $t_{2}=36$
is displayed in figure 6(b). The wave packet is seen to grow symmetrically about the ray
$t_{2}=36$
is displayed in figure 6(b). The wave packet is seen to grow symmetrically about the ray
![]() $v_{g}=0$
, and its streamwise extent is given by the spatio-temporal rays
$v_{g}=0$
, and its streamwise extent is given by the spatio-temporal rays
![]() $v_{g}^{+}$
and
$v_{g}^{+}$
and
![]() $v_{g}^{-}$
such that
$v_{g}^{-}$
such that
![]() ${\it\sigma}(v_{g}^{\pm })=0$
, i.e. the rays along which a neutral wave is observed. Because of the symmetric behaviour of the wave packet, these velocities are equal in magnitude.
${\it\sigma}(v_{g}^{\pm })=0$
, i.e. the rays along which a neutral wave is observed. Because of the symmetric behaviour of the wave packet, these velocities are equal in magnitude.

Figure 6. Evolution of the impulse response wave packet generated by a localized initial perturbation for
![]() $q=100$
and
$q=100$
and
![]() $p=0.25$
. (a) Time series of the amplitude
$p=0.25$
. (a) Time series of the amplitude
![]() $A(v_{g}t,t)$
observed along each spatio-temporal ray
$A(v_{g}t,t)$
observed along each spatio-temporal ray
![]() $x/t=v_{g}$
versus group velocity
$x/t=v_{g}$
versus group velocity
![]() $v_{g}$
and (b) corresponding growth rate
$v_{g}$
and (b) corresponding growth rate
![]() ${\it\sigma}(v_{g})$
evaluated from the amplitude at times
${\it\sigma}(v_{g})$
evaluated from the amplitude at times
![]() $t_{1}=18$
and
$t_{1}=18$
and
![]() $t_{2}=36$
. The streamwise extent of the wave packet is delineated by the leading- and trailing-edge velocities
$t_{2}=36$
. The streamwise extent of the wave packet is delineated by the leading- and trailing-edge velocities
![]() $v_{g}^{\pm }$
such that
$v_{g}^{\pm }$
such that
![]() ${\it\sigma}(v_{g}^{\pm })=0$
.
${\it\sigma}(v_{g}^{\pm })=0$
.
In the frame of the simulation that moves with the vortices, the absolute growth rate
![]() ${\it\sigma}(v_{g}=0)$
observed along the ray
${\it\sigma}(v_{g}=0)$
observed along the ray
![]() $x/t=v_{g}=0$
is positive, thus the instability is absolute and contaminates the whole domain. In reality, however, a street of shed vortices behind an obstacle is advected in the downstream direction due to the external flow. We therefore also consider that our system of point vortices moves horizontally at a certain positive velocity
$x/t=v_{g}=0$
is positive, thus the instability is absolute and contaminates the whole domain. In reality, however, a street of shed vortices behind an obstacle is advected in the downstream direction due to the external flow. We therefore also consider that our system of point vortices moves horizontally at a certain positive velocity
![]() $v_{a}>0$
, and we study the absolute or convective nature of the instability in the laboratory frame. Because of the Galilean invariance of the system, the absolute growth rate observed in that case is simply given by the growth rate measured along the ray
$v_{a}>0$
, and we study the absolute or convective nature of the instability in the laboratory frame. Because of the Galilean invariance of the system, the absolute growth rate observed in that case is simply given by the growth rate measured along the ray
![]() $x/t=v_{g}=-v_{a}$
in the frame of the vortices. Figure 6(b) shows that
$x/t=v_{g}=-v_{a}$
in the frame of the vortices. Figure 6(b) shows that
![]() ${\it\sigma}(v_{g}=-v_{a})$
becomes negative for values of
${\it\sigma}(v_{g}=-v_{a})$
becomes negative for values of
![]() $v_{a}$
larger than
$v_{a}$
larger than
![]() $|v_{g}^{-}|$
, revealing that the system becomes convectively unstable above a critical advection velocity
$|v_{g}^{-}|$
, revealing that the system becomes convectively unstable above a critical advection velocity
![]() $v_{a,0}=|v_{g}^{-}|$
.
$v_{a,0}=|v_{g}^{-}|$
.
The above numerical procedure is repeated for a range of values of the aspect ratio, and the magnitude of the trailing-edge velocity
![]() $|v_{g}^{-}|$
obtained in each case is plotted versus the aspect ratio
$|v_{g}^{-}|$
obtained in each case is plotted versus the aspect ratio
![]() $p$
in circles in figure 7. A steep decrease of
$p$
in circles in figure 7. A steep decrease of
![]() $|v_{g}^{-}|$
is observed as
$|v_{g}^{-}|$
is observed as
![]() $p$
approaches its temporally stable specific value
$p$
approaches its temporally stable specific value
![]() $p_{0}\simeq 0.281$
, implying that the critical advection velocity
$p_{0}\simeq 0.281$
, implying that the critical advection velocity
![]() $v_{a,0}$
above which the system becomes convectively unstable is lowered. Finally, note that the wave packet is observed to grow symmetrically about the ray
$v_{a,0}$
above which the system becomes convectively unstable is lowered. Finally, note that the wave packet is observed to grow symmetrically about the ray
![]() $v_{g}=0$
for all values of the aspect ratio, thus the leading-edge velocity
$v_{g}=0$
for all values of the aspect ratio, thus the leading-edge velocity
![]() $v_{g}^{+}$
is equal to
$v_{g}^{+}$
is equal to
![]() $|v_{g}^{-}|$
.
$|v_{g}^{-}|$
.

Figure 7. Magnitude of the trailing-edge velocity
![]() $|v_{g}^{-}|$
of the impulse response wave packet generated by a localized initial perturbation for the limiting unconfined case (
$|v_{g}^{-}|$
of the impulse response wave packet generated by a localized initial perturbation for the limiting unconfined case (
![]() $q=100$
) versus aspect ratio
$q=100$
) versus aspect ratio
![]() $p$
. Results from numerical simulations of the impulse response (circles) are compared with predictions from the unconfined analytical dispersion relation (solid line). In this unconfined situation, the leading-edge velocity has equal magnitude with the trailing-edge velocity.
$p$
. Results from numerical simulations of the impulse response (circles) are compared with predictions from the unconfined analytical dispersion relation (solid line). In this unconfined situation, the leading-edge velocity has equal magnitude with the trailing-edge velocity.
4.1.2 Results from the analytical dispersion relation
In this unconfined case, the dispersion relation
![]() ${\it\omega}={\it\omega}(k)$
assumes a simple form reported in Lamb (Reference Lamb1932) and Saffman (Reference Saffman1992), and is given in non-dimensional form by
${\it\omega}={\it\omega}(k)$
assumes a simple form reported in Lamb (Reference Lamb1932) and Saffman (Reference Saffman1992), and is given in non-dimensional form by
where one takes
![]() $+H$
and
$+H$
and
![]() $-H$
for the symmetrical and antisymmetrical modes respectively,
$-H$
for the symmetrical and antisymmetrical modes respectively,
![]() $s=\pm 1$
gives two solution branches for each mode and the coefficients
$s=\pm 1$
gives two solution branches for each mode and the coefficients
![]() $G$
,
$G$
,
![]() $H$
and
$H$
and
![]() $I$
are expressed as
$I$
are expressed as
where subscript
![]() $i$
denotes the imaginary part,
$i$
denotes the imaginary part,
![]() ${\it\omega}^{\prime }={\it\omega}^{\prime }(k)$
is the dispersion relation in a frame moving at group velocity
${\it\omega}^{\prime }={\it\omega}^{\prime }(k)$
is the dispersion relation in a frame moving at group velocity
![]() $v_{g}$
and expressed through the following Doppler shift
$v_{g}$
and expressed through the following Doppler shift
and
![]() $k^{\ast }$
is the complex wavenumber observed along the ray
$k^{\ast }$
is the complex wavenumber observed along the ray
![]() $x/t=v_{g}$
, which verifies the following saddle point condition
$x/t=v_{g}$
, which verifies the following saddle point condition
In addition, the Briggs–Bers criterion states that the saddle point
![]() $k^{\ast }$
must result from the pinching of two spatial branches
$k^{\ast }$
must result from the pinching of two spatial branches
![]() $k^{\pm }({\it\omega}^{\prime })=\{k({\it\omega}_{r}^{\prime }+\text{i}{\it\omega}_{i}^{\prime })\mid {\it\omega}_{r}^{\prime }\in \mathbb{R},{\it\omega}_{i}^{\prime }~\text{fixed}\}$
that originate in the lower and upper half-
$k^{\pm }({\it\omega}^{\prime })=\{k({\it\omega}_{r}^{\prime }+\text{i}{\it\omega}_{i}^{\prime })\mid {\it\omega}_{r}^{\prime }\in \mathbb{R},{\it\omega}_{i}^{\prime }~\text{fixed}\}$
that originate in the lower and upper half-
![]() $k$
-planes for sufficiently large positive values of
$k$
-planes for sufficiently large positive values of
![]() ${\it\omega}_{i}^{\prime }$
(Briggs Reference Briggs1964). As an example, figure 8 shows these spatial branches in the complex
${\it\omega}_{i}^{\prime }$
(Briggs Reference Briggs1964). As an example, figure 8 shows these spatial branches in the complex
![]() $k$
-plane, calculated as isolines of
$k$
-plane, calculated as isolines of
![]() ${\it\omega}_{i}^{\prime }(k)$
, and the saddle point
${\it\omega}_{i}^{\prime }(k)$
, and the saddle point
![]() $k^{\ast }$
resulting from the pinching of these branches as
$k^{\ast }$
resulting from the pinching of these branches as
![]() ${\it\omega}_{i}^{\prime }$
decreases, for
${\it\omega}_{i}^{\prime }$
decreases, for
![]() $p=0.3$
,
$p=0.3$
,
![]() $v_{g}=-1.62$
(figure 8
a) and
$v_{g}=-1.62$
(figure 8
a) and
![]() $p=0.35$
,
$p=0.35$
,
![]() $v_{g}=-2.03$
(figure 8
b). Note that jumps between the two solutions
$v_{g}=-2.03$
(figure 8
b). Note that jumps between the two solutions
![]() $s=\pm 1$
of
$s=\pm 1$
of
![]() ${\it\omega}(k)$
occur when the phase of the square root argument in (4.3) crosses
${\it\omega}(k)$
occur when the phase of the square root argument in (4.3) crosses
![]() ${\rm\pi}$
or
${\rm\pi}$
or
![]() $-{\rm\pi}$
, behaviour that has to be accounted for and corrected when plotting isolines of
$-{\rm\pi}$
, behaviour that has to be accounted for and corrected when plotting isolines of
![]() ${\it\omega}_{i}^{\prime }(k)$
. Once the saddle point
${\it\omega}_{i}^{\prime }(k)$
. Once the saddle point
![]() $k^{\ast }$
is located, the growth rate along the ray
$k^{\ast }$
is located, the growth rate along the ray
![]() $x/t=v_{g}$
can be calculated as
$x/t=v_{g}$
can be calculated as
![]() ${\it\sigma}(v_{g})={\it\omega}_{i}^{\prime }(k^{\ast }).$
Finally, the critical value of
${\it\sigma}(v_{g})={\it\omega}_{i}^{\prime }(k^{\ast }).$
Finally, the critical value of
![]() $v_{g}<0$
at which
$v_{g}<0$
at which
![]() ${\it\sigma}(v_{g})=0$
gives the trailing-edge velocity
${\it\sigma}(v_{g})=0$
gives the trailing-edge velocity
![]() $v_{g}^{-}$
of the impulse response wave packet. In this regard, the values of
$v_{g}^{-}$
of the impulse response wave packet. In this regard, the values of
![]() $v_{g}$
used in figure 8 give
$v_{g}$
used in figure 8 give
![]() ${\it\sigma}(v_{g})=0$
and thus correspond to
${\it\sigma}(v_{g})=0$
and thus correspond to
![]() $v_{g}^{-}$
for
$v_{g}^{-}$
for
![]() $p=0.3$
and 0.35.
$p=0.3$
and 0.35.

Figure 8. Spatial branches
![]() $k^{\pm }({\it\omega}^{\prime })$
of the Doppler-shifted unconfined dispersion relation (4.6) and saddle point
$k^{\pm }({\it\omega}^{\prime })$
of the Doppler-shifted unconfined dispersion relation (4.6) and saddle point
![]() $k^{\ast }$
resulting from the pinching of these branches as
$k^{\ast }$
resulting from the pinching of these branches as
![]() ${\it\omega}_{i}^{\prime }$
decreases, for (a)
${\it\omega}_{i}^{\prime }$
decreases, for (a)
![]() $p=0.3$
,
$p=0.3$
,
![]() $v_{g}=-1.62$
and (b)
$v_{g}=-1.62$
and (b)
![]() $p=0.35$
,
$p=0.35$
,
![]() $v_{g}=-2.03$
. In both cases, these critical values of
$v_{g}=-2.03$
. In both cases, these critical values of
![]() $v_{g}$
give
$v_{g}$
give
![]() ${\it\omega}_{i}^{\prime }(k^{\ast })={\it\sigma}(v_{g})=0$
and hence correspond to
${\it\omega}_{i}^{\prime }(k^{\ast })={\it\sigma}(v_{g})=0$
and hence correspond to
![]() $v_{g}^{-}$
.
$v_{g}^{-}$
.
Two different methods are used in order to locate numerically the saddle point
![]() $k^{\ast }$
and calculate
$k^{\ast }$
and calculate
![]() $v_{g}^{-}$
. When
$v_{g}^{-}$
. When
![]() $p<0.23$
or
$p<0.23$
or
![]() $p>0.32$
, the saddle point is computed in an iterative fashion by repeatedly fitting the function
$p>0.32$
, the saddle point is computed in an iterative fashion by repeatedly fitting the function
![]() ${\it\omega}^{\prime }(k)$
to a complex quadratic polynomial, each time leading to a new guess value for
${\it\omega}^{\prime }(k)$
to a complex quadratic polynomial, each time leading to a new guess value for
![]() $k^{\ast }$
, until convergence is achieved (Deissler Reference Deissler1987). Inside the range
$k^{\ast }$
, until convergence is achieved (Deissler Reference Deissler1987). Inside the range
![]() $0.23\leqslant p\leqslant 0.32$
, however, the saddle point
$0.23\leqslant p\leqslant 0.32$
, however, the saddle point
![]() $k^{\ast }$
is found by locating the minimum of the partial derivatives of
$k^{\ast }$
is found by locating the minimum of the partial derivatives of
![]() ${\it\omega}_{i}^{\prime }(k)$
along both
${\it\omega}_{i}^{\prime }(k)$
along both
![]() $k_{r}$
and
$k_{r}$
and
![]() $k_{i}$
directions, because its proximity with the real
$k_{i}$
directions, because its proximity with the real
![]() $k$
axis (as shown in figure 8
a) does not allow for a reliable complex quadratic fit. The resulting curve for
$k$
axis (as shown in figure 8
a) does not allow for a reliable complex quadratic fit. The resulting curve for
![]() $|v_{g}^{-}|$
as a function of
$|v_{g}^{-}|$
as a function of
![]() $p$
is displayed by the solid line in figure 7 and shows excellent agreement with the discrete values obtained previously from simulations of the impulse response. In addition to providing a further validation of the numerical method introduced in the previous section, the analytical curve reveals a cusp at the stable value of the aspect ratio
$p$
is displayed by the solid line in figure 7 and shows excellent agreement with the discrete values obtained previously from simulations of the impulse response. In addition to providing a further validation of the numerical method introduced in the previous section, the analytical curve reveals a cusp at the stable value of the aspect ratio
![]() $p_{0}=1/{\rm\pi}\sinh ^{-1}1$
. Intriguingly, this cusp saturates at a finite value of
$p_{0}=1/{\rm\pi}\sinh ^{-1}1$
. Intriguingly, this cusp saturates at a finite value of
![]() $|v_{g}^{-}|$
around 0.837, whereas one would expect
$|v_{g}^{-}|$
around 0.837, whereas one would expect
![]() $|v_{g}^{\pm }|$
to tend towards zero as the system approaches its stable configuration.
$|v_{g}^{\pm }|$
to tend towards zero as the system approaches its stable configuration.

Figure 9. Self-similar behaviour of the dispersion relation in a narrow range of
![]() $p$
around the stable value
$p$
around the stable value
![]() $p_{0}$
. (a) Temporal growth rate
$p_{0}$
. (a) Temporal growth rate
![]() ${\it\omega}_{i}(k)$
evaluated at
${\it\omega}_{i}(k)$
evaluated at
![]() $p=p_{0}+0.001$
, together with its elliptic approximation
$p=p_{0}+0.001$
, together with its elliptic approximation
![]() ${\it\omega}_{i}^{e}(k)$
and the definitions of
${\it\omega}_{i}^{e}(k)$
and the definitions of
![]() ${\it\omega}_{i,m}$
and
${\it\omega}_{i,m}$
and
![]() ${\rm\Delta}k$
. (b) Linear dependency of
${\rm\Delta}k$
. (b) Linear dependency of
![]() ${\it\omega}_{i,m}$
and
${\it\omega}_{i,m}$
and
![]() ${\rm\Delta}k$
on
${\rm\Delta}k$
on
![]() $p$
as the latter approaches
$p$
as the latter approaches
![]() $p_{0}$
.
$p_{0}$
.
This counter-intuitive property of the impulse response wave packet can be explained by the behaviour of the dispersion relation
![]() ${\it\omega}(k)$
for values of
${\it\omega}(k)$
for values of
![]() $p$
close to
$p$
close to
![]() $p_{0}$
. Figure 9(a) shows the temporal growth rate
$p_{0}$
. Figure 9(a) shows the temporal growth rate
![]() ${\it\omega}_{i}(k)$
evaluated at
${\it\omega}_{i}(k)$
evaluated at
![]() $p=p_{0}+0.001$
, together with the imaginary part of an elliptic approximation of
$p=p_{0}+0.001$
, together with the imaginary part of an elliptic approximation of
![]() ${\it\omega}(k)$
defined by
${\it\omega}(k)$
defined by
where
![]() $c$
is a real constant (numerical calculations indeed reveal that
$c$
is a real constant (numerical calculations indeed reveal that
![]() ${\it\omega}_{r}$
remains constant around
${\it\omega}_{r}$
remains constant around
![]() $k={\rm\pi}$
and
$k={\rm\pi}$
and
![]() $p=p_{0}$
),
$p=p_{0}$
),
![]() ${\it\omega}_{i,m}$
is the maximum temporal growth rate and
${\it\omega}_{i,m}$
is the maximum temporal growth rate and
![]() ${\rm\Delta}k$
is the half-width of the temporally unstable wavenumber region. Both
${\rm\Delta}k$
is the half-width of the temporally unstable wavenumber region. Both
![]() ${\it\omega}_{i,m}$
and
${\it\omega}_{i,m}$
and
![]() ${\rm\Delta}k$
depend on
${\rm\Delta}k$
depend on
![]() $p$
and are extracted from
$p$
and are extracted from
![]() ${\it\omega}_{i}(k)$
. Since the elliptic approximation
${\it\omega}_{i}(k)$
. Since the elliptic approximation
![]() ${\it\omega}^{e}(k)$
agrees extremely well with the exact dispersion relation, it may be employed instead of
${\it\omega}^{e}(k)$
agrees extremely well with the exact dispersion relation, it may be employed instead of
![]() ${\it\omega}(k)$
to derive an analytical expression for the edge velocities
${\it\omega}(k)$
to derive an analytical expression for the edge velocities
![]() $v_{g}^{\pm }$
of the impulse response, valid only for
$v_{g}^{\pm }$
of the impulse response, valid only for
![]() $p$
close to
$p$
close to
![]() $p_{0}$
. To that effect, we first calculate the complex wavenumber
$p_{0}$
. To that effect, we first calculate the complex wavenumber
![]() $k^{\ast }$
observed along the ray
$k^{\ast }$
observed along the ray
![]() $x/t=v_{g}$
and given by the saddle point condition (4.7)
$x/t=v_{g}$
and given by the saddle point condition (4.7)
 $$\begin{eqnarray}\frac{\partial {\it\omega}^{e}}{\partial k}(k^{\ast })=v_{g}\quad \Leftrightarrow \quad k^{\ast }={\rm\pi}+\text{i}\frac{{\rm\Delta}k^{2}v_{g}}{\sqrt{{\it\omega}_{i,m}^{2}-{\rm\Delta}k^{2}v_{g}^{2}}}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\partial {\it\omega}^{e}}{\partial k}(k^{\ast })=v_{g}\quad \Leftrightarrow \quad k^{\ast }={\rm\pi}+\text{i}\frac{{\rm\Delta}k^{2}v_{g}}{\sqrt{{\it\omega}_{i,m}^{2}-{\rm\Delta}k^{2}v_{g}^{2}}}.\end{eqnarray}$$
The growth rate along the ray
![]() $x/t=v_{g}$
can then be calculated with (4.5)
$x/t=v_{g}$
can then be calculated with (4.5)
Finally, setting
![]() ${\it\sigma}(v_{g})=0$
gives the edge velocities of the impulse response wave packet
${\it\sigma}(v_{g})=0$
gives the edge velocities of the impulse response wave packet
Figure 9(b) illustrates the dependency of
![]() ${\it\omega}_{i,m}$
and
${\it\omega}_{i,m}$
and
![]() ${\rm\Delta}k$
on the aspect ratio
${\rm\Delta}k$
on the aspect ratio
![]() $p$
as the latter tends towards its stable value
$p$
as the latter tends towards its stable value
![]() $p_{0}$
. A linear relationship is observed between all three quantities, implying that
$p_{0}$
. A linear relationship is observed between all three quantities, implying that
![]() $|v_{g}^{\pm }|$
converges to a constant value of
$|v_{g}^{\pm }|$
converges to a constant value of
![]() ${\it\omega}_{i,m}/{\rm\Delta}k\simeq 0.8377$
as
${\it\omega}_{i,m}/{\rm\Delta}k\simeq 0.8377$
as
![]() $p$
approaches
$p$
approaches
![]() $p_{0}$
, in perfect agreement with our previous findings. Therefore, it is the proportional decrease to zero of both
$p_{0}$
, in perfect agreement with our previous findings. Therefore, it is the proportional decrease to zero of both
![]() ${\it\omega}_{i,m}$
and
${\it\omega}_{i,m}$
and
![]() ${\rm\Delta}k$
as
${\rm\Delta}k$
as
![]() $p$
tends to
$p$
tends to
![]() $p_{0}$
, akin to a self-similar behaviour of the dispersion relation, that causes the impulse response wave packet to retain finite width while its height shrinks to zero when the system moves towards its stable configuration.
$p_{0}$
, akin to a self-similar behaviour of the dispersion relation, that causes the impulse response wave packet to retain finite width while its height shrinks to zero when the system moves towards its stable configuration.
4.2 Effect of the confinement
The influence of the confinement on the spatio-temporal properties of the impulse response of the vortex street is now investigated through numerical simulations at smaller values of the confinement ratio
![]() $q$
. Following the same procedure as before, the growth of the impulse response wave packet at
$q$
. Following the same procedure as before, the growth of the impulse response wave packet at
![]() $p=0.25$
and
$p=0.25$
and
![]() $q=1.5$
is illustrated in figure 10(a) through the time series of the amplitude
$q=1.5$
is illustrated in figure 10(a) through the time series of the amplitude
![]() $A(v_{g}t,t)$
observed along each spatio-temporal ray
$A(v_{g}t,t)$
observed along each spatio-temporal ray
![]() $x/t=v_{g}$
. The corresponding growth rate
$x/t=v_{g}$
. The corresponding growth rate
![]() ${\it\sigma}(v_{g})$
obtained from (4.2) with the amplitude at times
${\it\sigma}(v_{g})$
obtained from (4.2) with the amplitude at times
![]() $t_{1}=18$
and
$t_{1}=18$
and
![]() $t_{2}=36$
is displayed in figure 10(b). This time, the wave packet is no longer symmetric and grows asymmetrically about the ray
$t_{2}=36$
is displayed in figure 10(b). This time, the wave packet is no longer symmetric and grows asymmetrically about the ray
![]() $v_{g}=0$
, with its trailing-edge velocity
$v_{g}=0$
, with its trailing-edge velocity
![]() $v_{g}^{-}$
having greater magnitude than its leading-edge velocity
$v_{g}^{-}$
having greater magnitude than its leading-edge velocity
![]() $v_{g}^{+}$
. The confinement thus appears to break the symmetric behaviour of the impulse response that was observed in the unconfined case.
$v_{g}^{+}$
. The confinement thus appears to break the symmetric behaviour of the impulse response that was observed in the unconfined case.

Figure 10. Evolution of the impulse response wave packet generated by a localized initial perturbation for
![]() $q=1.5$
and
$q=1.5$
and
![]() $p=0.25$
. (a) Time series of the amplitude
$p=0.25$
. (a) Time series of the amplitude
![]() $A(v_{g}t,t)$
observed along each spatio-temporal ray
$A(v_{g}t,t)$
observed along each spatio-temporal ray
![]() $x/t=v_{g}$
versus group velocity
$x/t=v_{g}$
versus group velocity
![]() $v_{g}$
and (b) corresponding growth rate
$v_{g}$
and (b) corresponding growth rate
![]() ${\it\sigma}(v_{g})$
evaluated from the amplitude at times
${\it\sigma}(v_{g})$
evaluated from the amplitude at times
![]() $t_{1}=18$
and
$t_{1}=18$
and
![]() $t_{2}=36$
. The streamwise extent of the wave packet is delineated by the leading- and trailing-edge velocities
$t_{2}=36$
. The streamwise extent of the wave packet is delineated by the leading- and trailing-edge velocities
![]() $v_{g}^{\pm }$
such that
$v_{g}^{\pm }$
such that
![]() ${\it\sigma}(v_{g}^{\pm })=0$
.
${\it\sigma}(v_{g}^{\pm })=0$
.
This numerical procedure is repeated for a range of values of the confinement and aspect ratios, indicated by black lines in figure 4. Figure 11 shows the resulting leading- and trailing-edge velocities
![]() $v_{g}^{\pm }$
of the impulse response wave packet versus the aspect ratio
$v_{g}^{\pm }$
of the impulse response wave packet versus the aspect ratio
![]() $p$
, for two values of the confinement ratio,
$p$
, for two values of the confinement ratio,
![]() $q=1.6$
(figure 11
a) and 1.2 (figure 11
b). The calculated velocities are represented with dots and joined by straight lines. As the aspect ratio approaches the temporally stable specific value, the streamwise extent of the wave packet is reduced and its spatio-temporal expansion gradually shifts towards the negative
$q=1.6$
(figure 11
a) and 1.2 (figure 11
b). The calculated velocities are represented with dots and joined by straight lines. As the aspect ratio approaches the temporally stable specific value, the streamwise extent of the wave packet is reduced and its spatio-temporal expansion gradually shifts towards the negative
![]() $x$
direction. Comparing figures 11(a) and (b) shows that the confinement strongly affects the degree of asymmetry of the wave packet, to the point that the latter becomes convectively unstable in the frame of the simulation at
$x$
direction. Comparing figures 11(a) and (b) shows that the confinement strongly affects the degree of asymmetry of the wave packet, to the point that the latter becomes convectively unstable in the frame of the simulation at
![]() $q=1.2$
. The effect of the confinement is investigated in more detail in figure 12, where the leading- and trailing-edge velocities
$q=1.2$
. The effect of the confinement is investigated in more detail in figure 12, where the leading- and trailing-edge velocities
![]() $v_{g}^{\pm }$
are plotted versus the confinement ratio
$v_{g}^{\pm }$
are plotted versus the confinement ratio
![]() $q$
, for two values of the aspect ratio. It is observed that increasing the confinement at a given aspect ratio leads to a decrease in the signed values of both
$q$
, for two values of the aspect ratio. It is observed that increasing the confinement at a given aspect ratio leads to a decrease in the signed values of both
![]() $v_{g}^{+}$
and
$v_{g}^{+}$
and
![]() $v_{g}^{-}$
. While the sharp decrease observed in figure 12(a) for
$v_{g}^{-}$
. While the sharp decrease observed in figure 12(a) for
![]() $p=0.26$
can be attributed to the aspect ratio getting closer to the specific value for temporal stability as
$p=0.26$
can be attributed to the aspect ratio getting closer to the specific value for temporal stability as
![]() $q$
decreases (see figure 4), a steady decrease is also observed in figure 12(b) for
$q$
decreases (see figure 4), a steady decrease is also observed in figure 12(b) for
![]() $p=0.31$
even though the maximum temporal growth rate is approximately constant in this case.
$p=0.31$
even though the maximum temporal growth rate is approximately constant in this case.

Figure 11. Leading- and trailing-edge velocities
![]() $v_{g}^{\pm }$
of the impulse response wave packet generated by a localized initial perturbation versus aspect ratio
$v_{g}^{\pm }$
of the impulse response wave packet generated by a localized initial perturbation versus aspect ratio
![]() $p$
, for two values of the confinement ratio, (a)
$p$
, for two values of the confinement ratio, (a)
![]() $q=1.6$
and (b)
$q=1.6$
and (b)
![]() $q=1.2$
. The velocities given by the numerical simulations are represented with dots and joined by straight lines.
$q=1.2$
. The velocities given by the numerical simulations are represented with dots and joined by straight lines.

Figure 12. Leading- and trailing-edge velocities
![]() $v_{g}^{\pm }$
of the impulse response wave packet generated by a localized initial perturbation versus confinement ratio
$v_{g}^{\pm }$
of the impulse response wave packet generated by a localized initial perturbation versus confinement ratio
![]() $q$
, for two values of the aspect ratio, (a)
$q$
, for two values of the aspect ratio, (a)
![]() $p=0.26$
and (b)
$p=0.26$
and (b)
![]() $p=0.31$
. The velocities given by the numerical simulations are represented with dots and joined by straight lines.
$p=0.31$
. The velocities given by the numerical simulations are represented with dots and joined by straight lines.
In the reference frame of the vortices, the instability observed in figures 11 and 12 is either absolute or convective with both
![]() $v_{g}^{\pm }<0$
, in which case the impulse response wave packet propagates in the upstream direction. When taking into account the advection
$v_{g}^{\pm }<0$
, in which case the impulse response wave packet propagates in the upstream direction. When taking into account the advection
![]() $v_{a}$
of the vortices in the downstream direction, the relevant absolute to convective instability transition is nonetheless that giving rise to downstream propagation of the impulse wave packet. Thus, the critical advection velocity
$v_{a}$
of the vortices in the downstream direction, the relevant absolute to convective instability transition is nonetheless that giving rise to downstream propagation of the impulse wave packet. Thus, the critical advection velocity
![]() $v_{a,0}$
above which the instability becomes convective is like before given by
$v_{a,0}$
above which the instability becomes convective is like before given by
![]() $|v_{g}^{-}|$
. Consequently, the increase of
$|v_{g}^{-}|$
. Consequently, the increase of
![]() $|v_{g}^{-}|$
observed in figure 12 for decreasing values of
$|v_{g}^{-}|$
observed in figure 12 for decreasing values of
![]() $q$
implies that the confinement, remarkably, reinforces the absolute nature of the instability. This destabilizing effect of the confinement was also observed by Juniper (Reference Juniper2006, Reference Juniper2007) and Biancofiore & Gallaire (Reference Biancofiore and Gallaire2011) for the primary instability of confined two-dimensional jets and wakes.
$q$
implies that the confinement, remarkably, reinforces the absolute nature of the instability. This destabilizing effect of the confinement was also observed by Juniper (Reference Juniper2006, Reference Juniper2007) and Biancofiore & Gallaire (Reference Biancofiore and Gallaire2011) for the primary instability of confined two-dimensional jets and wakes.
5 Application to the vortex street in the wake of a cylinder
5.1 Stability of the Kármán vortex street in the near wake
The critical advection velocity
![]() $v_{a,0}$
given by our numerical technique remains to be compared with actual values of the advection velocity
$v_{a,0}$
given by our numerical technique remains to be compared with actual values of the advection velocity
![]() $v_{a}$
of the Kármán vortex street that develops past an obstacle in order to determine the absolute or convective nature of the instability. To that effect, we perform a direct numerical simulation (DNS) of the
$v_{a}$
of the Kármán vortex street that develops past an obstacle in order to determine the absolute or convective nature of the instability. To that effect, we perform a direct numerical simulation (DNS) of the
![]() $Re=100$
flow past a circular cylinder in the geometry shown in figure 13. The simulation is carried out in a confined channel and three different values 10, 8 and 6 are considered for the blockage ratio
$Re=100$
flow past a circular cylinder in the geometry shown in figure 13. The simulation is carried out in a confined channel and three different values 10, 8 and 6 are considered for the blockage ratio
![]() ${\it\beta}=H/D$
, where
${\it\beta}=H/D$
, where
![]() $H$
is the height of the channel and
$H$
is the height of the channel and
![]() $D$
the diameter of the cylinder. The details concerning the implementation of the DNS can be found in appendix B. In the following, all lengths are expressed in terms of the diameter
$D$
the diameter of the cylinder. The details concerning the implementation of the DNS can be found in appendix B. In the following, all lengths are expressed in terms of the diameter
![]() $D$
of the cylinder, and velocities are non-dimensionalized with the free-stream velocity
$D$
of the cylinder, and velocities are non-dimensionalized with the free-stream velocity
![]() $U$
.
$U$
.

Figure 13. Flow configuration for the DNS, frame of reference and computational domain.
For each value of the blockage ratio
![]() ${\it\beta}$
, the local properties
${\it\beta}$
, the local properties
![]() ${\it\Gamma}$
,
${\it\Gamma}$
,
![]() $a$
,
$a$
,
![]() $p$
,
$p$
,
![]() $q$
and the advection velocity
$q$
and the advection velocity
![]() $u_{a}$
of the vortex street are retrieved from the DNS at four different streamwise locations
$u_{a}$
of the vortex street are retrieved from the DNS at four different streamwise locations
![]() $x=10,20,30$
and 40, following the procedure detailed in appendix C. The local values of
$x=10,20,30$
and 40, following the procedure detailed in appendix C. The local values of
![]() $p$
and
$p$
and
![]() $q$
at each location are then fitted to our point vortex model, allowing for the obtention from our numerical technique of the corresponding critical advection velocity
$q$
at each location are then fitted to our point vortex model, allowing for the obtention from our numerical technique of the corresponding critical advection velocity
![]() $v_{a,0}=|v_{g}^{-}|$
above which the street becomes locally convectively unstable. Finally, this critical value is translated into the scale of the DNS via the relation
$v_{a,0}=|v_{g}^{-}|$
above which the street becomes locally convectively unstable. Finally, this critical value is translated into the scale of the DNS via the relation
The results are reported in table 1. The local advection velocities
![]() $u_{a}$
are much larger than the corresponding critical velocities
$u_{a}$
are much larger than the corresponding critical velocities
![]() $u_{a,0}$
for convective instability. This reveals that the vortex street is strongly convectively unstable at all considered streamwise locations and for all values of
$u_{a,0}$
for convective instability. This reveals that the vortex street is strongly convectively unstable at all considered streamwise locations and for all values of
![]() ${\it\beta}$
. Furthermore, the strength
${\it\beta}$
. Furthermore, the strength
![]() ${\it\Gamma}$
of the vortices is observed to decay by viscous diffusion as they are advected downstream of the cylinder, resulting in a decrease of the critical advection velocity
${\it\Gamma}$
of the vortices is observed to decay by viscous diffusion as they are advected downstream of the cylinder, resulting in a decrease of the critical advection velocity
![]() $u_{a,0}$
, as evidenced by (5.1). The vortex street will therefore remain convectively unstable further downstream of the cylinder. This rationalizes the intuition of Jiménez (Reference Jiménez1987) that ‘differences between the spatial development of natural wakes and the temporal evolution model’ would explain the persistence of natural vortex streets.
$u_{a,0}$
, as evidenced by (5.1). The vortex street will therefore remain convectively unstable further downstream of the cylinder. This rationalizes the intuition of Jiménez (Reference Jiménez1987) that ‘differences between the spatial development of natural wakes and the temporal evolution model’ would explain the persistence of natural vortex streets.
Table 1. Comparison of the advection velocity
![]() $u_{a}$
of the vortex street with the critical velocity
$u_{a}$
of the vortex street with the critical velocity
![]() $u_{a,0}$
for convective instability. The values of
$u_{a,0}$
for convective instability. The values of
![]() $St$
,
$St$
,
![]() ${\it\Gamma}$
,
${\it\Gamma}$
,
![]() $a$
,
$a$
,
![]() $p$
,
$p$
,
![]() $q$
and
$q$
and
![]() $u_{a}$
are retrieved from the DNS at various streamwise locations
$u_{a}$
are retrieved from the DNS at various streamwise locations
![]() $x$
. Our numerical technique based on the point vortex model is then invoked to obtain the corresponding local values of
$x$
. Our numerical technique based on the point vortex model is then invoked to obtain the corresponding local values of
![]() $u_{a,0}$
, and
$u_{a,0}$
, and
![]() $u_{a}^{m}$
is calculated with (5.2).
$u_{a}^{m}$
is calculated with (5.2).

Jiménez, however, also alluded to viscous effects as another possible explanation for this phenomena. In regard to viscosity, one might as well question the relevance of comparing advection velocities retrieved from a DNS of the viscous Navier–Stokes equations with critical velocities obtained from an idealistic point vortex model. These questions can be answered by approximating the advection velocity of the vortices with the inviscid model via the relation
where
![]() $v_{0}$
is the dimensional self-induced velocity given by (2.1). This relation symbolizes the idea that the vortices are advected at the free-stream velocity minus their self-induced velocity. It allows for an estimation of the error incurred by the use of the point vortex model and therefore the importance of viscous effects. The resulting approximate velocities are reported in table 1 and compare favourably with the values of
$v_{0}$
is the dimensional self-induced velocity given by (2.1). This relation symbolizes the idea that the vortices are advected at the free-stream velocity minus their self-induced velocity. It allows for an estimation of the error incurred by the use of the point vortex model and therefore the importance of viscous effects. The resulting approximate velocities are reported in table 1 and compare favourably with the values of
![]() $u_{a}$
retrieved from the DNS, both quantities following similar trends. More importantly, they both have the same order of magnitude, while values of
$u_{a}$
retrieved from the DNS, both quantities following similar trends. More importantly, they both have the same order of magnitude, while values of
![]() $u_{a}$
are larger by almost an order of magnitude compared with values of the critical velocity
$u_{a}$
are larger by almost an order of magnitude compared with values of the critical velocity
![]() $u_{a,0}$
. This confirms that viscous effects are negligible and that the persistence of natural vortex streets is due to the strongly convective nature of their inviscid instability.
$u_{a,0}$
. This confirms that viscous effects are negligible and that the persistence of natural vortex streets is due to the strongly convective nature of their inviscid instability.
Even though strongly convective, the instability could still be developing downstream, affecting the robustness of the vortex street. In order to quantify this effect, we calculate the spatial growth rate of the instability in the laboratory frame by applying Gaster’s transformation to the unconfined analytical dispersion relation (4.3). Extrapolating the non-dimensional advection velocity of the vortex street from the DNS results of the least confined case, we find that the maximum spatial growth rate is of the order of
![]() $-k_{i}\simeq 0.01$
, meaning that disturbances double in amplitude every 200 vortices. This negligible growth rate confirms that the vortex street is robust over a large distance downstream of the obstacle.
$-k_{i}\simeq 0.01$
, meaning that disturbances double in amplitude every 200 vortices. This negligible growth rate confirms that the vortex street is robust over a large distance downstream of the obstacle.
5.2 Possible relevance for the secondary street in the far wake
We now discuss if the secondary instability of the Kármán vortex street, despite being strongly convective with very small spatial growth rate, could still become significant sufficiently far downstream. Saffman & Schatzman (Reference Saffman and Schatzman1982a ) suggested indeed that the stability properties of the Kármán street could be relevant for the slow evolution process giving rise to the appearance of the ‘secondary vortex street’ first described by Taneda (Reference Taneda1959). These secondary vortex streets appear at approximately a hundred diameters downstream of the obstacle with a larger wavelength and smaller frequency than the primary street.
Since these first studies, there have been considerable efforts to explain the origin of the secondary vortex street and some debate regarding whether the mechanism is vortex merging or a mean flow instability. Matsui & Okude (Reference Matsui and Okude1983) made forced experiments showing the merging of two or three vortices depending on the forcing frequency. These vortex merging ideas were supported by theoretical and numerical work by Aref & Siggia (Reference Aref and Siggia1981) and Meiburg (Reference Meiburg1987). The experiments of Cimbala, Nagib & Roshko (Reference Cimbala, Nagib and Roshko1988), on the contrary, showed that the vortices of the primary vortex street have decayed at the point where the secondary street forms, and they argued that the frequency of the secondary street is unrelated to the vortex shedding frequency. They also performed a local stability analysis of the mean flow and computed the spatial growth with surprisingly good results for the dominant frequency considering various crude approximations. Williamson & Prasad (Reference Williamson and Prasad1993) confirmed the pertinence of the mean flow stability analysis of Cimbala et al. (Reference Cimbala, Nagib and Roshko1988) but also showed that the frequency of the secondary street is actually connected to the vortex shedding frequency through an extremely high sensitivity to free-stream disturbances, explaining also the observed variability between experimental facilities. These features are characteristic of convective instabilities. Accordingly, the more recent study of Kumar & Mittal (Reference Kumar and Mittal2012) was able to convincingly relate the secondary vortex street to a convectively unstable mode of the global flow.
Thus, the idea that the vortex merging dynamics could play a role on the formation of the secondary vortex street seems now largely dismissed in favour of the opposing view of a mean flow instability. However, as pointed out by Inoue & Yamazaki (Reference Inoue and Yamazaki1999) the two scenarios are compatible and whether the primary vortices have or not fully decayed at the appearance of the secondary street depends on the external forcing conditions. In our view, these are not mutually exclusive but rather complimentary approaches, neither of them considering the stability of the actual flow but rather constituting different approximations. The actual flow is indeed composed both of (i) a spatially evolving mean flow superimposed to (ii) a spatially evolving time-periodic train of downstream-travelling structures, with decreasing relative importance as the vortices of the primary instability progressively diffuse. While the potential influence of the former on the secondary vortex street formation is well captured by a global stability analysis of the mean flow, the present secondary stability analysis partially captures the role of the latter as well.
According to our present computations, the propagation velocity of the instability front is given by
![]() $u_{a}-u_{a,0}\simeq 0.87$
at the furthest downstream position in the least confined case, totally in line with the propagation velocity of 0.827–0.925 of the wave packets of the secondary vortex street reported by Kumar & Mittal (Reference Kumar and Mittal2012). Therefore, the appearance of the secondary vortex street is not inconsistent with the convective instability of the point vortex model.
$u_{a}-u_{a,0}\simeq 0.87$
at the furthest downstream position in the least confined case, totally in line with the propagation velocity of 0.827–0.925 of the wave packets of the secondary vortex street reported by Kumar & Mittal (Reference Kumar and Mittal2012). Therefore, the appearance of the secondary vortex street is not inconsistent with the convective instability of the point vortex model.
A more complete and rigorous approach would be to generalize the Floquet analysis of the temporally periodic primary vortex street of Henderson & Barkley (Reference Henderson and Barkley1996) by extending the domain size and looking for transient growth and receptivity.
6 Conclusions
In the present work, the classical problem of the stability of the Kármán vortex street has been re-examined under a spatio-temporal perspective. We based our analysis on the point vortex model of Rosenhead (Reference Rosenhead1929), accounting for the influence of confining walls, and we considered the vortices to be advected in the downstream direction at a certain unknown velocity. In this situation, numerical simulations of the linear impulse response of the system showed the existence of a critical advection velocity above which the street of point vortices becomes convectively unstable in the laboratory frame. This critical advection velocity was observed to decrease as the aspect ratio of the street approaches its temporally stable isolated value, and to increase with the confinement. In the unconfined limiting case, direct application of the Briggs–Bers criterion to the dispersion relation revealed that the critical advection velocity saturates to a non-zero value as the system tends to its stable aspect ratio. This remarkable property was explained by the self-similar behaviour of the dispersion relation when close to the stable aspect ratio.
Finally, the properties of an actual Kármán vortex street were retrieved at specified streamwise locations from the DNS of the
![]() $Re=100$
flow past a circular cylinder, under various degrees of confinement. Fitting these local properties to our point vortex model yielded the corresponding critical advection velocity of the vortices for local convective instability in each case. Comparing these values with the actual advection velocities recovered from the DNS indicated that the vortex street is strongly convectively unstable at all streamwise locations and for all considered degrees of confinement. This finally provides the point vortex model with an explanation for the permanence of Kármán streets at low Reynolds numbers despite their temporal instability to small perturbations, and proves that viscous effects are not responsible. The model is thus reconciled with the stability of the actual two-dimensional flow in the wake of a cylinder (Henderson & Barkley Reference Henderson and Barkley1996).
$Re=100$
flow past a circular cylinder, under various degrees of confinement. Fitting these local properties to our point vortex model yielded the corresponding critical advection velocity of the vortices for local convective instability in each case. Comparing these values with the actual advection velocities recovered from the DNS indicated that the vortex street is strongly convectively unstable at all streamwise locations and for all considered degrees of confinement. This finally provides the point vortex model with an explanation for the permanence of Kármán streets at low Reynolds numbers despite their temporal instability to small perturbations, and proves that viscous effects are not responsible. The model is thus reconciled with the stability of the actual two-dimensional flow in the wake of a cylinder (Henderson & Barkley Reference Henderson and Barkley1996).
More complicated patterns of vortices are observed in the wake of oscillating bodies (Williamson & Roshko Reference Williamson and Roshko1988), and it would be interesting to perform similar spatio-temporal instability analyses in these cases, still using simple inviscid models. Schnipper, Andersen & Bohr (Reference Schnipper, Andersen and Bohr2009) obtained a rich variety of these vortex wakes by varying the amplitude and frequency of the oscillation, with most of them showing strong downstream persistence. We therefore expect regular pattern of vortices to be convectively unstable in a wide range of configurations.
Acknowledgement
C.A. acknowledges the support of CONICYT/PAI, Apoyo al retorno desde el extranjero no. 821320055.
Appendix A. Coefficients of the dispersion relation
The coefficients
![]() $M$
,
$M$
,
![]() $N$
,
$N$
,
![]() $O$
,
$O$
,
![]() $P$
,
$P$
,
![]() $Q$
and
$Q$
and
![]() $R$
appearing in the dispersion relation of the confined Kármán vortex street in § 2.2 have the following expressions:
$R$
appearing in the dispersion relation of the confined Kármán vortex street in § 2.2 have the following expressions:
 $$\begin{eqnarray}\displaystyle N & = & \displaystyle -\frac{{\rm\pi}^{2}}{2q^{2}}\mathop{\sum }_{m=-\infty }^{\infty }\!\!\!\displaystyle \vphantom{\sum }^{\prime }\;[(E_{m}^{+}-F_{m}^{-})\text{e}^{\text{i}km}+(E_{m}^{+}+F_{m}^{-})]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{{\rm\pi}^{2}}{2q^{2}}\mathop{\sum }_{m=-\infty }^{\infty }(E_{m+1/2}^{-}+F_{m+1/2}^{+})-\frac{{\rm\pi}^{2}}{2q^{2}}\sec ^{2}\left(\frac{{\rm\pi}p}{2q}\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle N & = & \displaystyle -\frac{{\rm\pi}^{2}}{2q^{2}}\mathop{\sum }_{m=-\infty }^{\infty }\!\!\!\displaystyle \vphantom{\sum }^{\prime }\;[(E_{m}^{+}-F_{m}^{-})\text{e}^{\text{i}km}+(E_{m}^{+}+F_{m}^{-})]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{{\rm\pi}^{2}}{2q^{2}}\mathop{\sum }_{m=-\infty }^{\infty }(E_{m+1/2}^{-}+F_{m+1/2}^{+})-\frac{{\rm\pi}^{2}}{2q^{2}}\sec ^{2}\left(\frac{{\rm\pi}p}{2q}\right),\end{eqnarray}$$
Appendix B. Conditions for the DNS
The computational domain and the frame of reference for the DNS are shown in figure 13. Since our numerical method for the calculation of the critical advection velocity of the vortex street relies on an inviscid point vortex model, a uniform velocity profile
![]() $U$
is imposed at the entrance of the domain, together with a free-slip condition at the top and bottom walls. The Reynolds number
$U$
is imposed at the entrance of the domain, together with a free-slip condition at the top and bottom walls. The Reynolds number
![]() $Re=UD/{\it\nu}$
is set to 100, value at which vortex shedding is present (see Sahin & Owens Reference Sahin and Owens2004). The incompressible Navier–Stokes equations are solved with the software FreeFem++ and the computations are carried out on a mesh with 12 308 nodes and 23 986 triangular elements. A non-dimensional time step
$Re=UD/{\it\nu}$
is set to 100, value at which vortex shedding is present (see Sahin & Owens Reference Sahin and Owens2004). The incompressible Navier–Stokes equations are solved with the software FreeFem++ and the computations are carried out on a mesh with 12 308 nodes and 23 986 triangular elements. A non-dimensional time step
![]() $U/D\,{\rm\Delta}t$
equal to
$U/D\,{\rm\Delta}t$
equal to
![]() $0.05$
is used. In order to assess the adequacy of the spatial resolution, the value of the vortex shedding frequency
$0.05$
is used. In order to assess the adequacy of the spatial resolution, the value of the vortex shedding frequency
![]() $f$
, given in terms of the Strouhal number
$f$
, given in terms of the Strouhal number
![]() $St=fD/U$
, is monitored for the case
$St=fD/U$
, is monitored for the case
![]() ${\it\beta}=10$
. Increasing the mesh resolution to 16 575 nodes and 32 415 elements involved variations of the Strouhal number lower than 1.8 %, indicating convergence of the results.
${\it\beta}=10$
. Increasing the mesh resolution to 16 575 nodes and 32 415 elements involved variations of the Strouhal number lower than 1.8 %, indicating convergence of the results.
Appendix C. Retrieving vortex street properties from the DNS
In order to retrieve from the DNS the non-dimensional local properties
![]() ${\it\Gamma}$
,
${\it\Gamma}$
,
![]() $a$
,
$a$
,
![]() $p$
,
$p$
,
![]() $q$
and the advection velocity
$q$
and the advection velocity
![]() $u_{a}$
of the vortex street at various streamwise locations, we delineate at each considered location a fixed box of length 4.5 and height
$u_{a}$
of the vortex street at various streamwise locations, we delineate at each considered location a fixed box of length 4.5 and height
![]() $7.5{\it\beta}$
. The length of the box is chosen to be approximately one and a half that of each vortex, so that its circulation
$7.5{\it\beta}$
. The length of the box is chosen to be approximately one and a half that of each vortex, so that its circulation
![]() ${\it\Gamma}$
and centre coordinates may be obtained by integrating respectively the positive vorticity and its centre of mass over the box, at the time of crossing of a positive vortex. The vertical distance
${\it\Gamma}$
and centre coordinates may be obtained by integrating respectively the positive vorticity and its centre of mass over the box, at the time of crossing of a positive vortex. The vertical distance
![]() $h$
between the two rows of vortices can then be retrieved from the
$h$
between the two rows of vortices can then be retrieved from the
![]() $y$
coordinate of the vortex centre, while the advection velocity
$y$
coordinate of the vortex centre, while the advection velocity
![]() $u_{a}$
of the vortices is given by the time derivative of the
$u_{a}$
of the vortices is given by the time derivative of the
![]() $x$
coordinate. In addition, the Strouhal number of the flow can be obtained from the frequency spectrum of the time history of the
$x$
coordinate. In addition, the Strouhal number of the flow can be obtained from the frequency spectrum of the time history of the
![]() $x$
coordinate, from which the distance between consecutive vortices in the same row follows via the relation
$x$
coordinate, from which the distance between consecutive vortices in the same row follows via the relation
![]() $a=u_{a}/St$
. Finally, the aspect and confinement ratios are readily obtained with
$a=u_{a}/St$
. Finally, the aspect and confinement ratios are readily obtained with
![]() $p=h/a$
and
$p=h/a$
and
![]() $q=d/a$
, respectively.
$q=d/a$
, respectively.