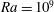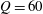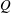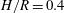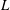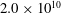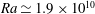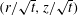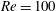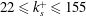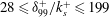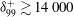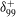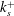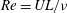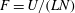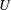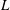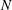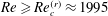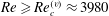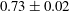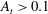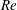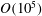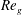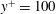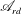Papers
Linear stability and energetics of rotating radial horizontal convection
-
- Published online by Cambridge University Press:
- 13 April 2016, pp. 1-35
-
- Article
- Export citation
Flow and fouling in a pleated membrane filter
-
- Published online by Cambridge University Press:
- 13 April 2016, pp. 36-59
-
- Article
- Export citation
Vapour-bubble nucleation and dynamics in turbulent Rayleigh–Bénard convection
-
- Published online by Cambridge University Press:
- 13 April 2016, pp. 60-95
-
- Article
- Export citation
Drop impact on a solid surface: short-time self-similarity
-
- Published online by Cambridge University Press:
- 13 April 2016, pp. 96-135
-
- Article
- Export citation
Defining coherent vortices objectively from the vorticity
-
- Published online by Cambridge University Press:
- 13 April 2016, pp. 136-173
-
- Article
- Export citation
On the coupled time-harmonic motion of a freely floating body and water covered by brash ice
-
- Published online by Cambridge University Press:
- 14 April 2016, pp. 174-186
-
- Article
- Export citation
Spatio-temporal stability of the Kármán vortex street and the effect of confinement
-
- Published online by Cambridge University Press:
- 14 April 2016, pp. 187-209
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Comparison of turbulent boundary layers over smooth and rough surfaces up to high Reynolds numbers
-
- Published online by Cambridge University Press:
- 14 April 2016, pp. 210-240
-
- Article
- Export citation
The admissibility domain of rarefaction shock waves in the near-critical vapour–liquid equilibrium region of pure typical fluids
-
- Published online by Cambridge University Press:
- 14 April 2016, pp. 241-261
-
- Article
- Export citation
Instability of a boundary layer flow on a vertical wall in a stably stratified fluid
-
- Published online by Cambridge University Press:
- 14 April 2016, pp. 262-277
-
- Article
- Export citation
An adjoint-based approach for finding invariant solutions of Navier–Stokes equations
-
- Published online by Cambridge University Press:
- 14 April 2016, pp. 278-312
-
- Article
- Export citation
Dynamics of buoyancy-driven flows at moderately high Atwood numbers
-
- Published online by Cambridge University Press:
- 14 April 2016, pp. 313-355
-
- Article
- Export citation
Turbulence collapse in a suction boundary layer
-
- Published online by Cambridge University Press:
- 14 April 2016, pp. 356-379
-
- Article
- Export citation
The evolution of a viscous thread pulled with a prescribed speed
-
- Published online by Cambridge University Press:
- 14 April 2016, pp. 380-408
-
- Article
- Export citation
Two-scale wave patterns on a periodically excited miscible liquid–liquid interface
-
- Published online by Cambridge University Press:
- 15 April 2016, pp. 409-422
-
- Article
- Export citation
On low-frequency variability of the midlatitude ocean gyres
-
- Published online by Cambridge University Press:
- 15 April 2016, pp. 423-442
-
- Article
- Export citation
Lift force on nanoparticles in shear flows of dilute gases: negative or positive?
-
- Published online by Cambridge University Press:
- 18 April 2016, pp. 443-454
-
- Article
- Export citation
Extension to nonlinear stability theory of the circular Couette flow
-
- Published online by Cambridge University Press:
- 19 April 2016, pp. 455-493
-
- Article
- Export citation
Development of turbulent boundary layers past a step change in wall roughness
-
- Published online by Cambridge University Press:
- 19 April 2016, pp. 494-523
-
- Article
- Export citation
Explicit expressions for eddy-diffusivity fields and effective large-scale advection in turbulent transport
-
- Published online by Cambridge University Press:
- 19 April 2016, pp. 524-548
-
- Article
- Export citation