1 Introduction
Suspension mechanics – the study of fluid containing solid particulates – has a long and distinguished history across more than a century. Einstein (Reference Einstein1906) showed that, for a dilute suspension of spheres at volume fraction
 $\unicode[STIX]{x1D719}$
in a fluid of viscosity
$\unicode[STIX]{x1D719}$
in a fluid of viscosity
 $\unicode[STIX]{x1D707}$
, to leading order in
$\unicode[STIX]{x1D707}$
, to leading order in
 $\unicode[STIX]{x1D719}$
the suspension acts as a Newtonian fluid having viscosity
$\unicode[STIX]{x1D719}$
the suspension acts as a Newtonian fluid having viscosity
Batchelor & Green (Reference Batchelor and Green1972) extended this result to the next order in
 $\unicode[STIX]{x1D719}$
, showing that, for steady extensional flows,
$\unicode[STIX]{x1D719}$
, showing that, for steady extensional flows,
but for shear flows the appearance of Jeffrey orbits, on which a pair of particles oscillate around one another indefinitely, makes it impossible to determine the viscosity. And as soon as interparticle forces are introduced, the rheology at order
 $\unicode[STIX]{x1D719}^{2}$
becomes non-Newtonian (Brady & Morris Reference Brady and Morris1997), with the suspension exhibiting first and second normal stress differences in steady simple shear flow.
$\unicode[STIX]{x1D719}^{2}$
becomes non-Newtonian (Brady & Morris Reference Brady and Morris1997), with the suspension exhibiting first and second normal stress differences in steady simple shear flow.
These results are for dilute suspensions – those having a very low solids volume fraction – and even with that strong simplification, we do not have a constitutive relation, a governing equation for the behaviour of these materials. The best attempt so far is by Phillips et al. (Reference Phillips, Armstrong, Brown, Graham and Abbott1992), who produced a model that captures shear-induced particle migration and a viscosity based on the local concentration of solids; but this model does not incorporate any microstructure beyond the concentration, nor predict any non-Newtonian effects.
The paper of Brady & Morris (Reference Brady and Morris1997) was seminal in its consideration of the microstructure: the arrangement of particles within the suspension. The most recent efforts in this area still draw on that early insight: such works as Fernandez et al. (Reference Fernandez, Mani, Rinaldi, Kadau, Mosquet, Lombois-Burger, Cayer-Barrioz, Herrman, Spencer and Isa2013), Heussinger (Reference Heussinger2013) and Seto et al. (Reference Seto, Mari, Morris and Denn2013) have used particle simulations to explore the microstructure emerging within shear flows under the influence of different forces between the particles. The most recent success in the area has been the reproduction of the phenomenon of discontinuous shear thickening, the abrupt increase in the steady shear viscosity of a suspension when the shear rate is increased beyond some critical rate. It is now widely accepted that a key ingredient of the phenomenon is ‘stress-induced friction’ (Mari et al.
Reference Mari, Seto, Morris and Denn2014; Wyart & Cates Reference Wyart and Cates2014), and this has been confirmed by experiment (Lin et al.
Reference Lin, Guy, Hermes, Ness, Sun, Poon and Cohen2015; Clavaud et al.
Reference Clavaud, Bérut, Metzger and Forterre2017).
However, real observations of thickening in practical flows are rarely in steady shear. We need to understand the evolution of the suspension microstructure and stress in other flows – steady and unsteady. This paper takes the first step in this process, by considering steady extensional flows.
2 Overview
The paper by Seto, Giusteri & Martiniello (Reference Seto, Giusteri and Martiniello2017) carries out particle dynamics simulations of concentrated suspensions in both shear and planar extensional flow. The authors use a combination of a repulsive force and frictional contact between particles, which gives similar behaviour to the stress-induced friction model of contact between particles that has been so successful of late in reproducing discontinuous shear thickening, and they investigate the microstructure of the suspension and its average stress during the flow.
In shear they simply reproduce observations we have seen before, which nonetheless bear repeating. For slow flows below the shear-thickening transition, there is substantial long-range ordering within the flow, as particles line up in the flow direction. Above the transition, frictive contacts between particles disrupt the structure, and there is global disorder. This has widely been accepted as being a fundamental part of the mechanism of shear thickening.
However, there are two key extensions here. Let us look first at the change of flow type. In steady planar extensional flow, the authors find that there is no global ordering even at low flow rates. This is not a huge surprise, as there are no straight streamlines along which the particles could align. We see the clear differences between shear and extensional flows in figure 1, in which we plot the pair distribution function
 $g(\boldsymbol{r})$
, which describes the likelihood of finding a particle centred at a given location given that one test particle is centred at the origin. In (a) are plots for shear flow below and above the shear-thickening transition. The global ordering at low flow rates is very clear. In (b) are plots for low and high strain rates in plane extension flow. Although there are differences between them, they are qualitatively very similar: there is no order–disorder transition.
$g(\boldsymbol{r})$
, which describes the likelihood of finding a particle centred at a given location given that one test particle is centred at the origin. In (a) are plots for shear flow below and above the shear-thickening transition. The global ordering at low flow rates is very clear. In (b) are plots for low and high strain rates in plane extension flow. Although there are differences between them, they are qualitatively very similar: there is no order–disorder transition.
Figure 1. (a) The pair distribution function
 $g(\boldsymbol{r})$
below (left) and above (right) thickening for simple shear flow of a monodisperse suspension. (b) Equivalent plots for planar extensional flow. From Seto et al. (Reference Seto, Giusteri and Martiniello2017, figure 6).
$g(\boldsymbol{r})$
below (left) and above (right) thickening for simple shear flow of a monodisperse suspension. (b) Equivalent plots for planar extensional flow. From Seto et al. (Reference Seto, Giusteri and Martiniello2017, figure 6).
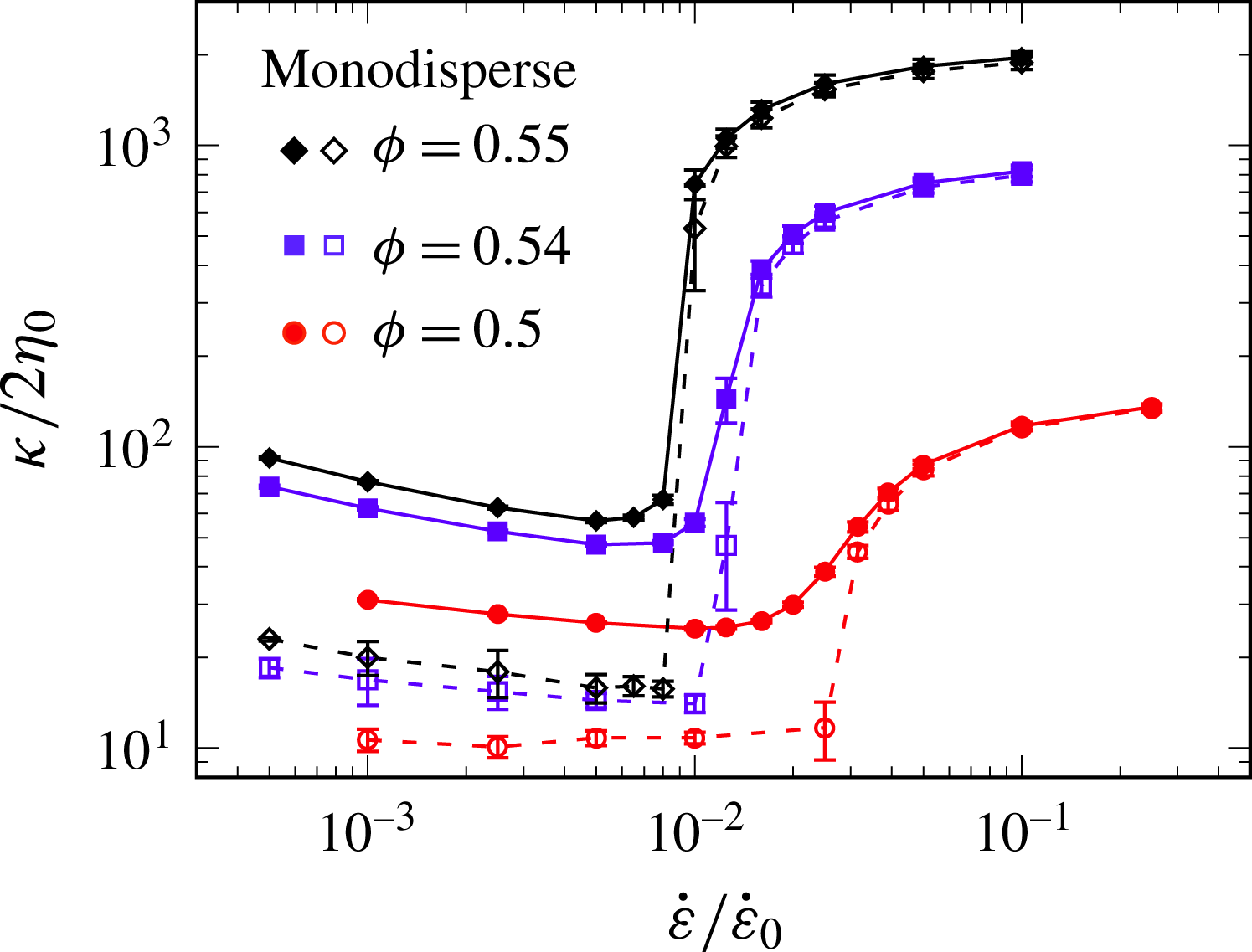
It is surprising that, despite the lack of an order–disorder transition, we see thickening in extensional flow just as we do in shear. There are subtleties in the definition of the flow rate, and of the viscous contribution to the stress, in these different flows; but using a coherent convention introduced by Giusteri & Seto (Reference Giusteri and Seto2017) they can plot viscosity against flow rate for both flows on the same graph (figure 2). The thickening is not quite as extreme in extensional flow as in shear, but it is quite unarguably discontinuous thickening.
Figure 2. Plots of effective viscosity against flow rate for suspensions at different volume fractions. Solid symbols, solid lines: extensional flow. Open symbols, dashed lines: shear flow. From Seto et al. (Reference Seto, Giusteri and Martiniello2017, figure 2).
The second key extension in this paper is to move away from monodisperse suspensions and (as a proxy for true polydispersity) use spheres of two different sizes. Even weak polydispersity (size ratio of 1.2) has the effect of breaking up the long-range order in slow shear flow, without making much difference to the shear thickening in the suspension. Polydispersity makes shear flow look very much like extension.
It is therefore clear that the mechanism of shear thickening is not closely tied to the disruption of long-range order within the suspension; the long-range order itself is a symptom of the idealisations made in earlier simulations (perfect monodispersity and pure shearing flow).
The authors go on to investigate their microstructure further and find that the key to thickening is in the distribution of contacting particle pairs. These pairs are all (necessarily) the same distance apart, so their angular distribution is all that matters: and this angular distribution changes dramatically at the thickening transition, in both shear and extensional flows. Below thickening, the contacts are largely in a single direction (or absent in shear flow); above thickening, there is a wide angular distribution. This indicates that the key factor in thickening is the development of a contact network, with force chains running throughout the suspension. The microstructure also causes non-Newtonian effects in both flow types.
3 Future
A key challenge of suspension mechanics is the generation of a constitutive model that can be used for complex flows: flows with too much spatial variation for full particle simulations to be practicable. Such a constitutive model would need to take into account the underlying mechanisms of shear (and indeed extension) thickening, as well as the construction and destruction of microstructure by flow.
An immediate next step from the current work may be to investigate crossover flows between shear and extension; or flows whose strength varies with time, and the processes governing the evolution of the microstructure. But there is no question that this first foray into extensional flows of suspensions is a key step towards our goals.

$g(\boldsymbol{r})$ below (left) and above (right) thickening for simple shear flow of a monodisperse suspension. (b) Equivalent plots for planar extensional flow. From Seto et al. (2017, figure 6).




1 Introduction
Suspension mechanics – the study of fluid containing solid particulates – has a long and distinguished history across more than a century. Einstein (Reference Einstein1906) showed that, for a dilute suspension of spheres at volume fraction $\unicode[STIX]{x1D719}$
in a fluid of viscosity
$\unicode[STIX]{x1D719}$
in a fluid of viscosity
 $\unicode[STIX]{x1D707}$
, to leading order in
$\unicode[STIX]{x1D707}$
, to leading order in
 $\unicode[STIX]{x1D719}$
the suspension acts as a Newtonian fluid having viscosity
$\unicode[STIX]{x1D719}$
the suspension acts as a Newtonian fluid having viscosity
Batchelor & Green (Reference Batchelor and Green1972) extended this result to the next order in $\unicode[STIX]{x1D719}$
, showing that, for steady extensional flows,
$\unicode[STIX]{x1D719}$
, showing that, for steady extensional flows,
but for shear flows the appearance of Jeffrey orbits, on which a pair of particles oscillate around one another indefinitely, makes it impossible to determine the viscosity. And as soon as interparticle forces are introduced, the rheology at order $\unicode[STIX]{x1D719}^{2}$
becomes non-Newtonian (Brady & Morris Reference Brady and Morris1997), with the suspension exhibiting first and second normal stress differences in steady simple shear flow.
$\unicode[STIX]{x1D719}^{2}$
becomes non-Newtonian (Brady & Morris Reference Brady and Morris1997), with the suspension exhibiting first and second normal stress differences in steady simple shear flow.
These results are for dilute suspensions – those having a very low solids volume fraction – and even with that strong simplification, we do not have a constitutive relation, a governing equation for the behaviour of these materials. The best attempt so far is by Phillips et al. (Reference Phillips, Armstrong, Brown, Graham and Abbott1992), who produced a model that captures shear-induced particle migration and a viscosity based on the local concentration of solids; but this model does not incorporate any microstructure beyond the concentration, nor predict any non-Newtonian effects.
The paper of Brady & Morris (Reference Brady and Morris1997) was seminal in its consideration of the microstructure: the arrangement of particles within the suspension. The most recent efforts in this area still draw on that early insight: such works as Fernandez et al. (Reference Fernandez, Mani, Rinaldi, Kadau, Mosquet, Lombois-Burger, Cayer-Barrioz, Herrman, Spencer and Isa2013), Heussinger (Reference Heussinger2013) and Seto et al. (Reference Seto, Mari, Morris and Denn2013) have used particle simulations to explore the microstructure emerging within shear flows under the influence of different forces between the particles. The most recent success in the area has been the reproduction of the phenomenon of discontinuous shear thickening, the abrupt increase in the steady shear viscosity of a suspension when the shear rate is increased beyond some critical rate. It is now widely accepted that a key ingredient of the phenomenon is ‘stress-induced friction’ (Mari et al. Reference Mari, Seto, Morris and Denn2014; Wyart & Cates Reference Wyart and Cates2014), and this has been confirmed by experiment (Lin et al. Reference Lin, Guy, Hermes, Ness, Sun, Poon and Cohen2015; Clavaud et al. Reference Clavaud, Bérut, Metzger and Forterre2017).
However, real observations of thickening in practical flows are rarely in steady shear. We need to understand the evolution of the suspension microstructure and stress in other flows – steady and unsteady. This paper takes the first step in this process, by considering steady extensional flows.
2 Overview
The paper by Seto, Giusteri & Martiniello (Reference Seto, Giusteri and Martiniello2017) carries out particle dynamics simulations of concentrated suspensions in both shear and planar extensional flow. The authors use a combination of a repulsive force and frictional contact between particles, which gives similar behaviour to the stress-induced friction model of contact between particles that has been so successful of late in reproducing discontinuous shear thickening, and they investigate the microstructure of the suspension and its average stress during the flow.
In shear they simply reproduce observations we have seen before, which nonetheless bear repeating. For slow flows below the shear-thickening transition, there is substantial long-range ordering within the flow, as particles line up in the flow direction. Above the transition, frictive contacts between particles disrupt the structure, and there is global disorder. This has widely been accepted as being a fundamental part of the mechanism of shear thickening.
However, there are two key extensions here. Let us look first at the change of flow type. In steady planar extensional flow, the authors find that there is no global ordering even at low flow rates. This is not a huge surprise, as there are no straight streamlines along which the particles could align. We see the clear differences between shear and extensional flows in figure 1, in which we plot the pair distribution function $g(\boldsymbol{r})$
, which describes the likelihood of finding a particle centred at a given location given that one test particle is centred at the origin. In (a) are plots for shear flow below and above the shear-thickening transition. The global ordering at low flow rates is very clear. In (b) are plots for low and high strain rates in plane extension flow. Although there are differences between them, they are qualitatively very similar: there is no order–disorder transition.
$g(\boldsymbol{r})$
, which describes the likelihood of finding a particle centred at a given location given that one test particle is centred at the origin. In (a) are plots for shear flow below and above the shear-thickening transition. The global ordering at low flow rates is very clear. In (b) are plots for low and high strain rates in plane extension flow. Although there are differences between them, they are qualitatively very similar: there is no order–disorder transition.
Figure 1. (a) The pair distribution function $g(\boldsymbol{r})$
below (left) and above (right) thickening for simple shear flow of a monodisperse suspension. (b) Equivalent plots for planar extensional flow. From Seto et al. (Reference Seto, Giusteri and Martiniello2017, figure 6).
$g(\boldsymbol{r})$
below (left) and above (right) thickening for simple shear flow of a monodisperse suspension. (b) Equivalent plots for planar extensional flow. From Seto et al. (Reference Seto, Giusteri and Martiniello2017, figure 6).
It is surprising that, despite the lack of an order–disorder transition, we see thickening in extensional flow just as we do in shear. There are subtleties in the definition of the flow rate, and of the viscous contribution to the stress, in these different flows; but using a coherent convention introduced by Giusteri & Seto (Reference Giusteri and Seto2017) they can plot viscosity against flow rate for both flows on the same graph (figure 2). The thickening is not quite as extreme in extensional flow as in shear, but it is quite unarguably discontinuous thickening.
Figure 2. Plots of effective viscosity against flow rate for suspensions at different volume fractions. Solid symbols, solid lines: extensional flow. Open symbols, dashed lines: shear flow. From Seto et al. (Reference Seto, Giusteri and Martiniello2017, figure 2).
The second key extension in this paper is to move away from monodisperse suspensions and (as a proxy for true polydispersity) use spheres of two different sizes. Even weak polydispersity (size ratio of 1.2) has the effect of breaking up the long-range order in slow shear flow, without making much difference to the shear thickening in the suspension. Polydispersity makes shear flow look very much like extension.
It is therefore clear that the mechanism of shear thickening is not closely tied to the disruption of long-range order within the suspension; the long-range order itself is a symptom of the idealisations made in earlier simulations (perfect monodispersity and pure shearing flow).
The authors go on to investigate their microstructure further and find that the key to thickening is in the distribution of contacting particle pairs. These pairs are all (necessarily) the same distance apart, so their angular distribution is all that matters: and this angular distribution changes dramatically at the thickening transition, in both shear and extensional flows. Below thickening, the contacts are largely in a single direction (or absent in shear flow); above thickening, there is a wide angular distribution. This indicates that the key factor in thickening is the development of a contact network, with force chains running throughout the suspension. The microstructure also causes non-Newtonian effects in both flow types.
3 Future
A key challenge of suspension mechanics is the generation of a constitutive model that can be used for complex flows: flows with too much spatial variation for full particle simulations to be practicable. Such a constitutive model would need to take into account the underlying mechanisms of shear (and indeed extension) thickening, as well as the construction and destruction of microstructure by flow.
An immediate next step from the current work may be to investigate crossover flows between shear and extension; or flows whose strength varies with time, and the processes governing the evolution of the microstructure. But there is no question that this first foray into extensional flows of suspensions is a key step towards our goals.