Article contents
Self-similar mean dynamics in turbulent wall flows
Published online by Cambridge University Press: 08 February 2013
Abstract
This study investigates how and why dynamical self-similarities emerge with increasing Reynolds number within the canonical wall flows beyond the transitional regime. An overarching aim is to advance a mechanistically coherent description of turbulent wall-flow dynamics that is mathematically tractable and grounded in the mean dynamical equations. As revealed by the analysis of Fife, Klewicki & Wei (J. Discrete Continuous Dyn. Syst. A, vol. 24, 2009, pp. 781–807), the equations that respectively describe the mean dynamics of turbulent channel, pipe and boundary layer flows formally admit invariant forms. These expose an underlying self-similar structure. In all cases, two kinds of dynamical self-similarity are shown to exist on an internal domain that, for all Reynolds numbers, extends from 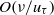 $O(\nu / {u}_{\tau } )$ to
$O(\nu / {u}_{\tau } )$ to 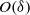 $O(\delta )$, where
$O(\delta )$, where  $\nu $ is the kinematic viscosity,
$\nu $ is the kinematic viscosity, 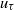 ${u}_{\tau } $ is the friction velocity and
${u}_{\tau } $ is the friction velocity and  $\delta $ is the half-channel height, pipe radius, or boundary layer thickness. The simpler of the two self-similarities is operative on a large outer portion of the relevant domain. This self-similarity leads to an explicit analytical closure of the mean momentum equation. This self-similarity also underlies the emergence of a logarithmic mean velocity profile. A more complicated kind a self-similarity emerges asymptotically over a smaller domain closer to the wall. The simpler self-similarity allows the mean dynamical equation to be written as a closed system of nonlinear ordinary differential equations that, like the similarity solution for the laminar flat-plate boundary layer, can be numerically integrated. The resulting similarity solutions are demonstrated to exhibit nearly exact agreement with direct numerical simulations over the solution domain specified by the theory. At the Reynolds numbers investigated, the outer similarity solution is shown to be operative over a domain that encompasses
$\delta $ is the half-channel height, pipe radius, or boundary layer thickness. The simpler of the two self-similarities is operative on a large outer portion of the relevant domain. This self-similarity leads to an explicit analytical closure of the mean momentum equation. This self-similarity also underlies the emergence of a logarithmic mean velocity profile. A more complicated kind a self-similarity emerges asymptotically over a smaller domain closer to the wall. The simpler self-similarity allows the mean dynamical equation to be written as a closed system of nonlinear ordinary differential equations that, like the similarity solution for the laminar flat-plate boundary layer, can be numerically integrated. The resulting similarity solutions are demonstrated to exhibit nearly exact agreement with direct numerical simulations over the solution domain specified by the theory. At the Reynolds numbers investigated, the outer similarity solution is shown to be operative over a domain that encompasses 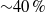 ${\sim }40\hspace{0.167em} \% $ of the overall width of the flow. Other properties predicted by the theory are also shown to be well supported by existing data.
${\sim }40\hspace{0.167em} \% $ of the overall width of the flow. Other properties predicted by the theory are also shown to be well supported by existing data.
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 57
- Cited by


