Article contents
On the equatorial Ekman layer
Published online by Cambridge University Press: 30 August 2016
Abstract
The steady incompressible viscous flow in the wide gap between spheres rotating rapidly about a common axis at slightly different rates (small Rossby number) has a long and celebrated history. The problem is relevant to the dynamics of geophysical and planetary core flows, for which, in the case of electrically conducting fluids, the possible operation of a dynamo is of considerable interest. A comprehensive asymptotic study, in the small Ekman number limit 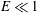 $E\ll 1$, was undertaken by Stewartson (J. Fluid Mech., vol. 26, 1966, pp. 131–144). The mainstream flow, exterior to the
$E\ll 1$, was undertaken by Stewartson (J. Fluid Mech., vol. 26, 1966, pp. 131–144). The mainstream flow, exterior to the 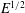 $E^{1/2}$ Ekman layers on the inner/outer boundaries and the shear layer on the inner sphere tangent cylinder
$E^{1/2}$ Ekman layers on the inner/outer boundaries and the shear layer on the inner sphere tangent cylinder 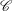 $\mathscr{C}$, is geostrophic. Stewartson identified a complicated nested layer structure on
$\mathscr{C}$, is geostrophic. Stewartson identified a complicated nested layer structure on 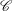 $\mathscr{C}$, which comprises relatively thick quasigeostrophic
$\mathscr{C}$, which comprises relatively thick quasigeostrophic  $E^{2/7}$- (inside
$E^{2/7}$- (inside 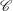 $\mathscr{C}$) and
$\mathscr{C}$) and 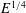 $E^{1/4}$- (outside
$E^{1/4}$- (outside 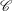 $\mathscr{C}$) layers. They embed a thinner ageostrophic
$\mathscr{C}$) layers. They embed a thinner ageostrophic 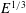 $E^{1/3}$ shear layer (on
$E^{1/3}$ shear layer (on 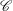 $\mathscr{C}$), which merges with the inner sphere Ekman layer to form the
$\mathscr{C}$), which merges with the inner sphere Ekman layer to form the 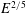 $E^{2/5}$-equatorial Ekman layer of axial length
$E^{2/5}$-equatorial Ekman layer of axial length 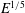 $E^{1/5}$. Under appropriate scaling, this
$E^{1/5}$. Under appropriate scaling, this 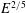 $E^{2/5}$-layer problem may be formulated, correct to leading order, independent of
$E^{2/5}$-layer problem may be formulated, correct to leading order, independent of 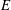 $E$. Then the Ekman boundary layer and ageostrophic shear layer become features of the far-field (as identified by the large value of the scaled axial coordinate
$E$. Then the Ekman boundary layer and ageostrophic shear layer become features of the far-field (as identified by the large value of the scaled axial coordinate  $z$) solution. We present a numerical solution of the previously unsolved equatorial Ekman layer problem using a non-local integral boundary condition at finite
$z$) solution. We present a numerical solution of the previously unsolved equatorial Ekman layer problem using a non-local integral boundary condition at finite  $z$ to account for the far-field behaviour. Adopting
$z$ to account for the far-field behaviour. Adopting 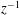 $z^{-1}$ as a small parameter we extend Stewartson’s similarity solution for the ageostrophic shear layer to higher orders. This far-field solution agrees well with that obtained from our numerical model.
$z^{-1}$ as a small parameter we extend Stewartson’s similarity solution for the ageostrophic shear layer to higher orders. This far-field solution agrees well with that obtained from our numerical model.
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
Footnotes
Present address: Département de Mathématiques et Applications, CNRS UMR-8553, École Normale Supérieure, 45 rue d’Ulm, 75005 Paris, France
References
- 12
- Cited by



