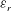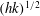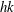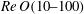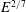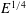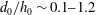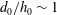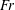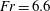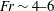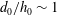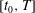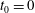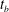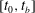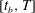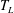Papers
Instability of a vortex sheet leaving a right-angled wedge
-
- Published online by Cambridge University Press:
- 15 August 2016, pp. 1-17
-
- Article
- Export citation
The evolution of local instability regions in turbulent non-premixed flames
-
- Published online by Cambridge University Press:
- 15 August 2016, pp. 18-50
-
- Article
- Export citation
The effects of Ekman pumping on quasi-geostrophic Rayleigh–Bénard convection
-
- Published online by Cambridge University Press:
- 16 August 2016, pp. 51-71
-
- Article
- Export citation
Rotating horizontal convection and the potential vorticity constraint
-
- Published online by Cambridge University Press:
- 16 August 2016, pp. 72-93
-
- Article
- Export citation
Oscillatory Marangoni flows with inertia
-
- Published online by Cambridge University Press:
- 19 August 2016, pp. 94-118
-
- Article
- Export citation
Numerical investigation of the flow over a model transonic turbine blade tip
-
- Published online by Cambridge University Press:
- 17 August 2016, pp. 119-143
-
- Article
- Export citation
Chaotic mixing in three-dimensional porous media
-
- Published online by Cambridge University Press:
- 17 August 2016, pp. 144-174
-
- Article
- Export citation
Transition in the asymptotic suction boundary layer over a heated plate
-
- Published online by Cambridge University Press:
- 19 August 2016, pp. 175-199
-
- Article
- Export citation
Effect of surfactant on motion and deformation of compound droplets in arbitrary unbounded Stokes flows
-
- Published online by Cambridge University Press:
- 19 August 2016, pp. 200-249
-
- Article
- Export citation
Higher-order dissipation in the theory of homogeneous isotropic turbulence
-
- Published online by Cambridge University Press:
- 19 August 2016, pp. 250-274
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Current generation by deep-water breaking waves
-
- Published online by Cambridge University Press:
- 22 August 2016, pp. 275-291
-
- Article
- Export citation
Wave modulation: the geometry, kinematics, and dynamics of surface-wave packets
-
- Published online by Cambridge University Press:
- 19 August 2016, pp. 292-312
-
- Article
- Export citation
Deceleration of droplets that glide along the free surface of a bath
-
- Published online by Cambridge University Press:
- 19 August 2016, pp. 313-331
-
- Article
- Export citation
On the global nonlinear instability of the rotating-disk flow over a finite domain
-
- Published online by Cambridge University Press:
- 22 August 2016, pp. 332-355
-
- Article
- Export citation
Multiscale analysis of the topological invariants in the logarithmic region of turbulent channels at a friction Reynolds number of 932
-
- Published online by Cambridge University Press:
- 30 August 2016, pp. 356-394
-
- Article
- Export citation
On the equatorial Ekman layer
-
- Published online by Cambridge University Press:
- 30 August 2016, pp. 395-435
-
- Article
- Export citation
Supercritical dead water: effect of nonlinearity and comparison with observations
-
- Published online by Cambridge University Press:
- 30 August 2016, pp. 436-465
-
- Article
- Export citation
Optimal perturbations in time-dependent variable-density Kelvin–Helmholtz billows
-
- Published online by Cambridge University Press:
- 30 August 2016, pp. 466-501
-
- Article
- Export citation
Oscillatory convection and limitations of the Boussinesq approximation
-
- Published online by Cambridge University Press:
- 30 August 2016, pp. 502-515
-
- Article
- Export citation
Maximum drop radius and critical Weber number for splashing in the dynamical Leidenfrost regime
-
- Published online by Cambridge University Press:
- 30 August 2016, pp. 516-527
-
- Article
- Export citation