1 Introduction
1.1 Anatomical and physiological considerations
The cerebrospinal fluid (CSF) is a colourless fluid that is continuously secreted from the blood plasma in the choroid plexus of the brain ventricles and fills the subarachnoid space (SAS), bathing the external surfaces of the brain and the spinal cord, as shown schematically in figure 1. At normal body temperatures, the CSF is an incompressible Newtonian fluid with constant density
![]() $\unicode[STIX]{x1D70C}$
and kinematic viscosity
$\unicode[STIX]{x1D70C}$
and kinematic viscosity
![]() $\unicode[STIX]{x1D708}$
similar to those of water. The CSF is reabsorbed back into the venous circulation at fingerlike projections of the arachnoid membrane called villi and may also drain into the lymphatic vessels around the cranial cavity (Davson Reference Davson1966; Cutler et al.
Reference Cutler, Page, Galicich and Watters1968; Milhorat et al.
Reference Milhorat, Hammock, Fenstermacher, Rall and Levin1971; Milhorat Reference Milhorat1975; Chikly Reference Chikly1998; Boulton et al.
Reference Boulton, Flessner, Armstrong, Mohamed, Hay and Johnston1999; Orešković & Klarica Reference Orešković and Klarica2010). Its primary mechanical functions are to cushion the brain within the skull, thus serving as a shock absorber for the central nervous system (CNS), and to reduce the compression exerted by the brain on the stem of the spinal cord by buoyancy effects. CSF also plays an important physiological function by maintaining the electrolytic environment, transporting hormones, circulating nutrients and chemicals filtered from the blood, and removing waste products from the cell metabolism of the brain and the CNS (Greitz, Franck & Nordell Reference Greitz, Franck and Nordell1993; Greitz & Hannerz Reference Greitz and Hannerz1996; Pollay Reference Pollay2010). Therefore, it is generally accepted that the absence of CSF circulation around the CNS may compromise its normal physiologic functions (Whedon & Glassey Reference Whedon and Glassey2009).
$\unicode[STIX]{x1D708}$
similar to those of water. The CSF is reabsorbed back into the venous circulation at fingerlike projections of the arachnoid membrane called villi and may also drain into the lymphatic vessels around the cranial cavity (Davson Reference Davson1966; Cutler et al.
Reference Cutler, Page, Galicich and Watters1968; Milhorat et al.
Reference Milhorat, Hammock, Fenstermacher, Rall and Levin1971; Milhorat Reference Milhorat1975; Chikly Reference Chikly1998; Boulton et al.
Reference Boulton, Flessner, Armstrong, Mohamed, Hay and Johnston1999; Orešković & Klarica Reference Orešković and Klarica2010). Its primary mechanical functions are to cushion the brain within the skull, thus serving as a shock absorber for the central nervous system (CNS), and to reduce the compression exerted by the brain on the stem of the spinal cord by buoyancy effects. CSF also plays an important physiological function by maintaining the electrolytic environment, transporting hormones, circulating nutrients and chemicals filtered from the blood, and removing waste products from the cell metabolism of the brain and the CNS (Greitz, Franck & Nordell Reference Greitz, Franck and Nordell1993; Greitz & Hannerz Reference Greitz and Hannerz1996; Pollay Reference Pollay2010). Therefore, it is generally accepted that the absence of CSF circulation around the CNS may compromise its normal physiologic functions (Whedon & Glassey Reference Whedon and Glassey2009).
In healthy humans, CSF secretion and reabsorption are balanced, maintaining a constant mean intracranial pressure. In adults, there are
![]() $140{-}170~\text{ml}$
of CSF at any given time, of which approximately 30 ml are in the four ventricles of the brain,
$140{-}170~\text{ml}$
of CSF at any given time, of which approximately 30 ml are in the four ventricles of the brain,
![]() $70{-}80~\text{ml}$
in the cerebral subarachnoid space, and
$70{-}80~\text{ml}$
in the cerebral subarachnoid space, and
![]() $V=40{-}60~\text{ml}$
in the spinal SAS Ambarki et al.
Reference Ambarki, Lindqvist, Wåhlin, Petterson, Warntjes, Birgander, Malm and Eklund2012. In normal physiological conditions, the mean rate of CSF production and reabsorption is
$V=40{-}60~\text{ml}$
in the spinal SAS Ambarki et al.
Reference Ambarki, Lindqvist, Wåhlin, Petterson, Warntjes, Birgander, Malm and Eklund2012. In normal physiological conditions, the mean rate of CSF production and reabsorption is
![]() $0.3{-}0.4~\text{ml}~\text{min}^{-1}$
(
$0.3{-}0.4~\text{ml}~\text{min}^{-1}$
(
![]() $400{-}600~\text{ml}~\text{day}^{-1}$
) which means that the entire volume of CSF bathing the CNS is replaced every 6–10 h (Davson Reference Davson1966; Milhorat Reference Milhorat1969; Johanson et al.
Reference Johanson, Duncan, Klinge, Brinker, Stopa and Silverberg2008; Pardridge Reference Pardridge2011).
$400{-}600~\text{ml}~\text{day}^{-1}$
) which means that the entire volume of CSF bathing the CNS is replaced every 6–10 h (Davson Reference Davson1966; Milhorat Reference Milhorat1969; Johanson et al.
Reference Johanson, Duncan, Klinge, Brinker, Stopa and Silverberg2008; Pardridge Reference Pardridge2011).
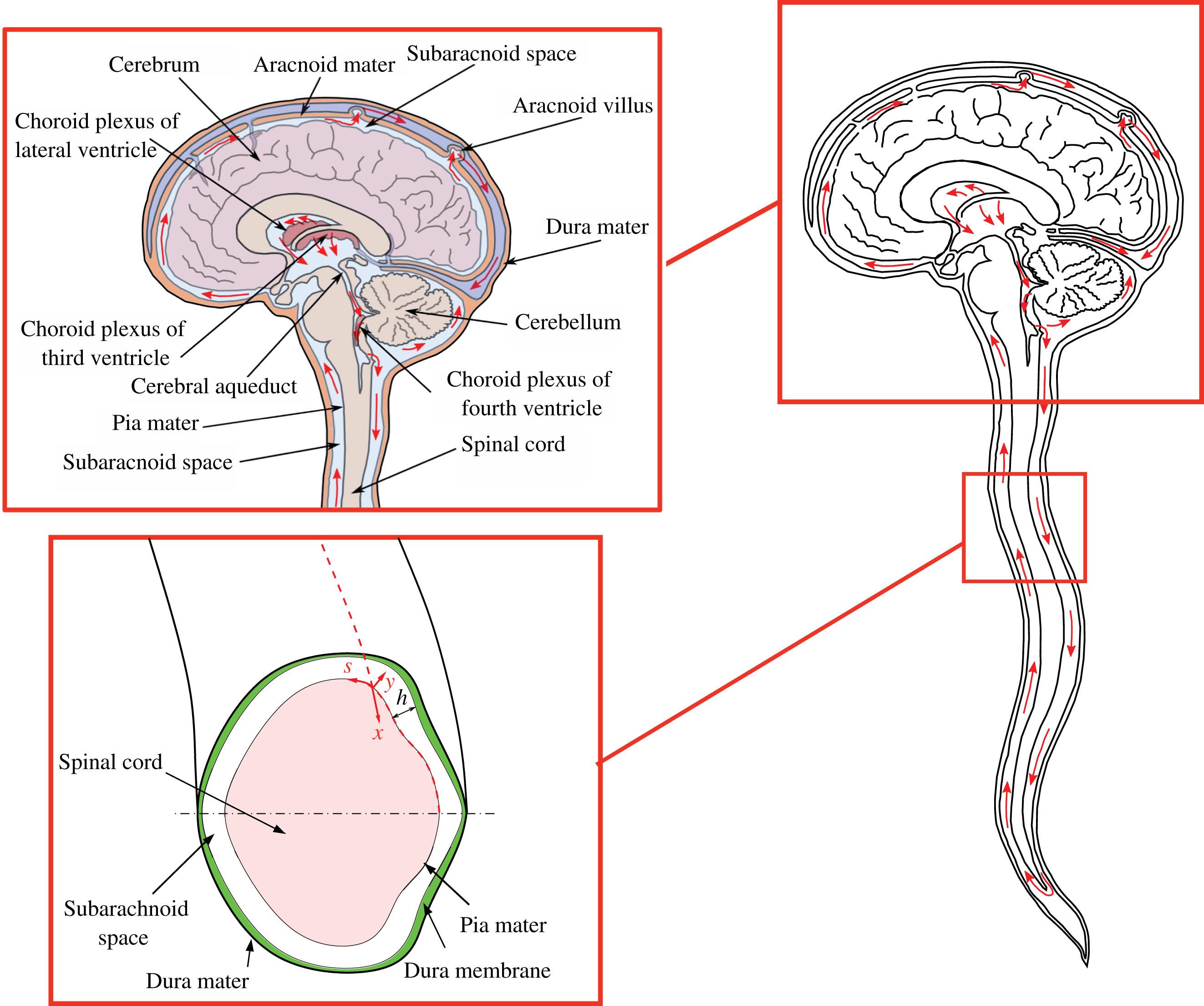
The volume of the cranial vault is filled by the brain, the CSF and blood, and is enclosed by the rigid skull, which is connected at its base (foramen magnum) to a compliant slender spinal canal enclosing the spinal cord, of length
![]() $L\sim 60{-}80~\text{cm}$
. The spinal SAS, filled with CSF, is a thin annular canal bounded internally by the pia mater, which surrounds the spinal cord, and externally by the deformable dura membrane, as indicated in figure 1. The average intracranial volume in an adult is 1700 ml, with the brain tissue composing approximately 1400 ml, and the balance comprised of the CSF and blood.
$L\sim 60{-}80~\text{cm}$
. The spinal SAS, filled with CSF, is a thin annular canal bounded internally by the pia mater, which surrounds the spinal cord, and externally by the deformable dura membrane, as indicated in figure 1. The average intracranial volume in an adult is 1700 ml, with the brain tissue composing approximately 1400 ml, and the balance comprised of the CSF and blood.
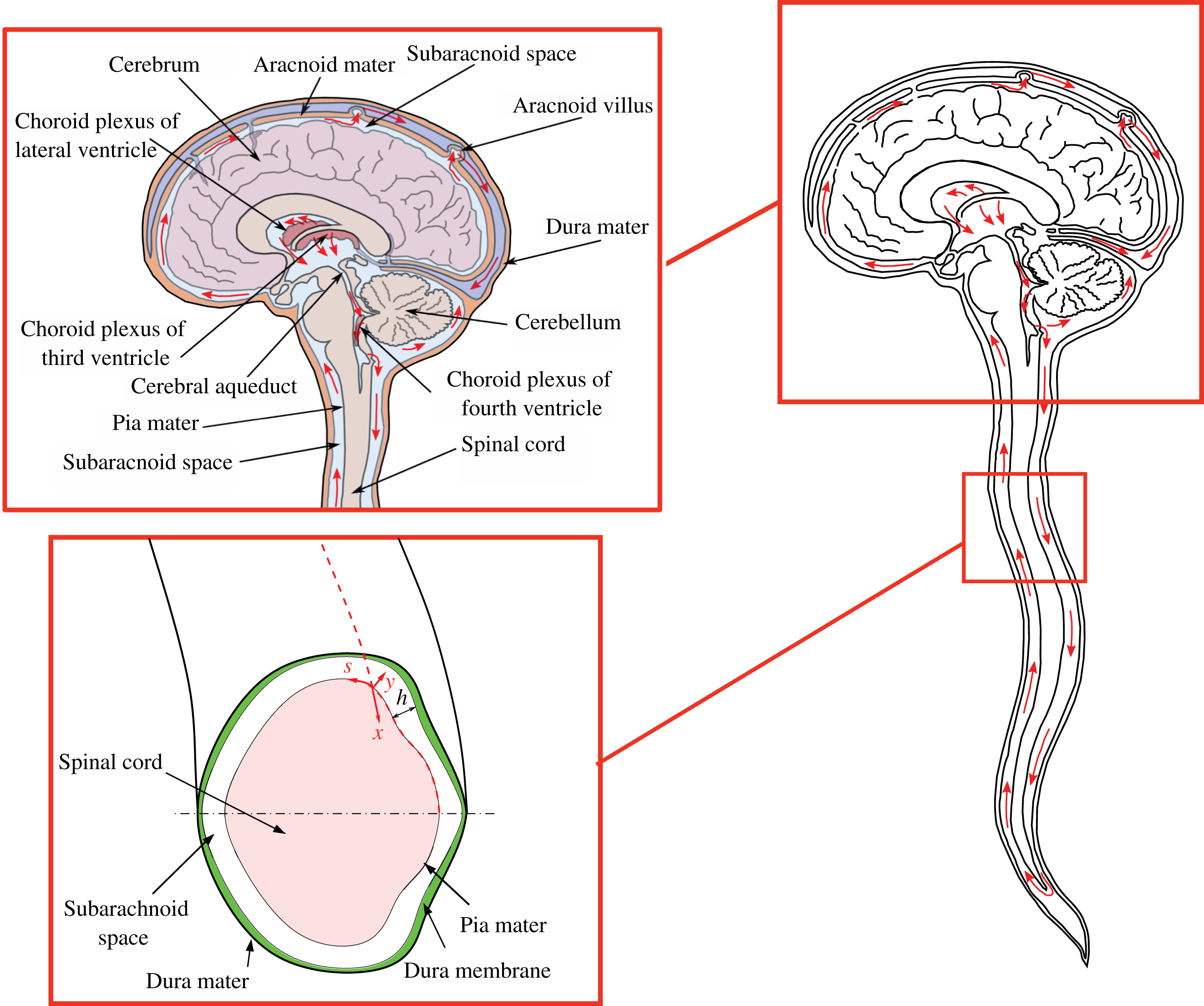
Figure 1. Schematic view of the anatomical features of the cranial cavity and the spinal canal, with indication of the curvilinear coordinates used in the analysis and of the bulk motion of the CSF in the spinal canal.
1.2 Observed CSF circulation
With each heart beat the volume oscillations of the blood flowing in and out of the rigid cranial vault cause the intracranial pressure to change in a time–periodic fashion with an approximate frequency of 1 Hz (Nitz et al.
Reference Nitz, Bradley, Watanabe, Lee, Burgoyne, O’Sullivan and Herbst1992; Bhadelia et al.
Reference Bhadelia, Bogdan, Kaplan and Wolpert1997; Wagshul et al.
Reference Wagshul, Chen, Egnor, McCormack and Roche2006; Wagshul, Eide & Madsen Reference Wagshul, Eide and Madsen2011). This pressure fluctuation drives CSF periodically in and out of the compliant spinal canal (Loth, Yardimci & Alperin Reference Loth, Yardimci and Alperin2001), as needed to ensure that the sum of the volumes of the brain, CSF and the intracranial blood in the rigid cranial vault remains constant, following a straightforward conservation-of-mass principle known in the neurological community as the Monro–Kellie doctrine or hypothesis (Mokri Reference Mokri2001). The oscillating CSF flow in the spinal canal is accommodated by the displacement of the venous flow and the compression of the venous and fatty tissue in the epidural space that surrounds the dural sac, which, in turn, determines the effective elastic properties (compliance) of the spinal canal. In healthy adults, the tidal volume displaced in and out across the foramen magnum and into the cervical SAS during each cardiac cycle is
![]() $\unicode[STIX]{x0394}V\sim 1{-}2~\text{ml}$
of CSF, corresponding to a very small fraction
$\unicode[STIX]{x0394}V\sim 1{-}2~\text{ml}$
of CSF, corresponding to a very small fraction
![]() $\unicode[STIX]{x0394}V/V\sim 0.02{-}0.03$
of the total CSF volume inside the spinal canal. The associated stroke length
$\unicode[STIX]{x0394}V/V\sim 0.02{-}0.03$
of the total CSF volume inside the spinal canal. The associated stroke length
![]() $S=(\unicode[STIX]{x0394}V/V)L\sim 1$
cm is much smaller than the canal length
$S=(\unicode[STIX]{x0394}V/V)L\sim 1$
cm is much smaller than the canal length
![]() $L$
, resulting in oscillatory velocities
$L$
, resulting in oscillatory velocities
![]() $u\sim (\unicode[STIX]{x0394}V/V)\unicode[STIX]{x1D714}L$
, where
$u\sim (\unicode[STIX]{x0394}V/V)\unicode[STIX]{x1D714}L$
, where
![]() $\unicode[STIX]{x1D714}\simeq 2\unicode[STIX]{x03C0}~\text{rad}~\text{s}^{-1}$
is the relevant angular frequency. Magnetic resonance imaging (MRI) measurements have shown that the amplitude of these velocity fluctuations, on the order of a few centimetres per second near the foramen magnum, progressively decreases as one moves downwards along the length of the canal to reach zero value at its closed–end sacral region (Loth et al.
Reference Loth, Yardimci and Alperin2001; Haughton & Mardal Reference Haughton and Mardal2014). It has also been observed in many radiological studies that, in addition of the pulsatility of the arterial blood flow supplying the cranial vault, the respiration also produces a modulation of the intracranial pressure, resulting in a smaller additional oscillation of the CSF in the spinal canal at a lower frequency (12–18 cycles per minute in adults) (Kao et al.
Reference Kao, Guo, Liou, Hsiao and Chou2008; Dreha-Kulaczewski et al.
Reference Dreha-Kulaczewski, Joseph, Merboldt, Ludwig, Gärtner and Frahm2015). An overview of the current knowledge of pulsatile CSF motion can be found in the excellent review by Linninger et al. (Reference Linninger, Tangen, Hsu and Frim2016).
$\unicode[STIX]{x1D714}\simeq 2\unicode[STIX]{x03C0}~\text{rad}~\text{s}^{-1}$
is the relevant angular frequency. Magnetic resonance imaging (MRI) measurements have shown that the amplitude of these velocity fluctuations, on the order of a few centimetres per second near the foramen magnum, progressively decreases as one moves downwards along the length of the canal to reach zero value at its closed–end sacral region (Loth et al.
Reference Loth, Yardimci and Alperin2001; Haughton & Mardal Reference Haughton and Mardal2014). It has also been observed in many radiological studies that, in addition of the pulsatility of the arterial blood flow supplying the cranial vault, the respiration also produces a modulation of the intracranial pressure, resulting in a smaller additional oscillation of the CSF in the spinal canal at a lower frequency (12–18 cycles per minute in adults) (Kao et al.
Reference Kao, Guo, Liou, Hsiao and Chou2008; Dreha-Kulaczewski et al.
Reference Dreha-Kulaczewski, Joseph, Merboldt, Ludwig, Gärtner and Frahm2015). An overview of the current knowledge of pulsatile CSF motion can be found in the excellent review by Linninger et al. (Reference Linninger, Tangen, Hsu and Frim2016).
In a seminal radionuclide scanning study, Di Chiro (Reference Di Chiro1964) reported the upward migration of a labeled compound from the lumbar region of the spinal canal to the cranial vault. He also showed the rapid migration of the compound injected in the brain ventricles downwards into the spinal canal (Di Chiro Reference Di Chiro1966; Di Chiro et al.
Reference Di Chiro, Larson, Harrington, Johnston, Green and Swann1973). These findings, which were later corroborated by numerous radiological studies (Levy & Di Chiro Reference Levy and Di Chiro1990; Greitz & Hannerz Reference Greitz and Hannerz1996; Castillo Reference Castillo2016), gave partial support to the hypothesis that in addition to the observed biphasic periodic tides of ebb-and-flow described above, there must be an active circulation mechanism associated with transport of CSF produced by the choroid plexus into the spinal canal and returning a portion of it back to the cranial vault. Following Di Chiro’s experiments there have been numerous radiological observations confirming that in adult humans the tracer injected in the lumbar region is detected moving upwards and reaching the basal cisterns of the cranial vault in 15–20 min (see, for example, the measurements of Greitz & Hannerz (Reference Greitz and Hannerz1996)). These observations suggest that the characteristic velocities of the bulk motion of the CSF along the spinal canal are on the order of
![]() $1~\text{cm}~\text{min}^{-1}$
. However, even though all current physiology text books depict this bulk recirculation (right-hand side sketch in figure 1), the existence of this slow-moving, bulk recirculation of the CSF in the spinal canal has continued to be the subject of dispute for the past 50 years. To date, more than 50 years after Di Chiro’s radiological observations, there has been no comprehensive physical explanation for the mechanism responsible for the establishment of such a bulk motion. Understanding the mechanism that regulates this bulk motion of the CSF in the spinal canal has important implications in optimizing targeted drug delivery systems to the intrathecal space (injections in the CSF surrounding the spinal cord) (Lanz et al.
Reference Lanz, Däubler, Eissner, Brod and Theiss1986; Kroin et al.
Reference Kroin, Ali, York and Penn1993; Penn Reference Penn2003; Nelissen Reference Nelissen2008; Hettiarachchi et al.
Reference Hettiarachchi, Hsu, Harris and Linninger2011; Bottros & Christo Reference Bottros and Christo2014), and in improving the current understanding of the etiology of a large class of neurological conditions. This lack of a conclusive description of the physical mechanism responsible for the establishment of this slow recirculating flow in the spinal canal has motivated us to address the question of whether a periodic pressure pulsation in the rigid cranial vault could also induce a bulk recirculating flow along the length of the compliant spinal canal. In addition, the work is motivated by the important physiological question of how the characteristics of this bulk recirculating motion could be deregulated due to specific anatomical characteristics and other physiological parameters (i.e. changes in the compliance of the spinal canal due to ageing, increased blood pressure, cardiac rate, etc.).
$1~\text{cm}~\text{min}^{-1}$
. However, even though all current physiology text books depict this bulk recirculation (right-hand side sketch in figure 1), the existence of this slow-moving, bulk recirculation of the CSF in the spinal canal has continued to be the subject of dispute for the past 50 years. To date, more than 50 years after Di Chiro’s radiological observations, there has been no comprehensive physical explanation for the mechanism responsible for the establishment of such a bulk motion. Understanding the mechanism that regulates this bulk motion of the CSF in the spinal canal has important implications in optimizing targeted drug delivery systems to the intrathecal space (injections in the CSF surrounding the spinal cord) (Lanz et al.
Reference Lanz, Däubler, Eissner, Brod and Theiss1986; Kroin et al.
Reference Kroin, Ali, York and Penn1993; Penn Reference Penn2003; Nelissen Reference Nelissen2008; Hettiarachchi et al.
Reference Hettiarachchi, Hsu, Harris and Linninger2011; Bottros & Christo Reference Bottros and Christo2014), and in improving the current understanding of the etiology of a large class of neurological conditions. This lack of a conclusive description of the physical mechanism responsible for the establishment of this slow recirculating flow in the spinal canal has motivated us to address the question of whether a periodic pressure pulsation in the rigid cranial vault could also induce a bulk recirculating flow along the length of the compliant spinal canal. In addition, the work is motivated by the important physiological question of how the characteristics of this bulk recirculating motion could be deregulated due to specific anatomical characteristics and other physiological parameters (i.e. changes in the compliance of the spinal canal due to ageing, increased blood pressure, cardiac rate, etc.).
1.3 Potential physical mechanisms
Several different physical processes have been postulated to account for the observed transport of radiological markers up and down the spinal canal. These include partial CSF reabsorption within the spinal canal and shear-enhanced diffusion. Although there is a lack of precise measurements, it appears that the spinal canal is not a major site of CSF reabsortion (Lorenzo, Page & Watters Reference Lorenzo, Page and Watters2016). Nevertheless, reabsorption of CSF in the spinal canal will contribute to a downward transport but it cannot explain the upward migration of the traces towards the cranial vault reported in numerous radiological studies. An alternative physical mechanism that may contribute to enhance the spreading of the tracers is shear-enhanced diffusion, often also referred to as Taylor diffusion (Taylor Reference Taylor1953; Watson Reference Watson1983; Yasuda Reference Yasuda1984), i.e. transverse diffusion coupled with the underlying radial shear of the oscillatory motion along the canal. However, because of the small diffusivity of the tracer, approximately
![]() $\unicode[STIX]{x1D705}=5\times 10^{-10}~\text{m}^{2}~\text{s}^{-1}$
, the resulting enhanced diffusion velocities are much too small to explain the radiological observations. To see this, one may begin by writing
$\unicode[STIX]{x1D705}=5\times 10^{-10}~\text{m}^{2}~\text{s}^{-1}$
, the resulting enhanced diffusion velocities are much too small to explain the radiological observations. To see this, one may begin by writing
![]() $K=\unicode[STIX]{x1D705}(1+{\mathcal{R}})$
for the coefficient of enhanced diffusivity due to shear in an oscillatory flow in a pipe. This expression was obtained by Watson (Reference Watson1983) by assuming a linear gradient for the concentration of the passive scalar along the canal. For an oscillatory motion with stroke length
$K=\unicode[STIX]{x1D705}(1+{\mathcal{R}})$
for the coefficient of enhanced diffusivity due to shear in an oscillatory flow in a pipe. This expression was obtained by Watson (Reference Watson1983) by assuming a linear gradient for the concentration of the passive scalar along the canal. For an oscillatory motion with stroke length
![]() $S$
in a channel of characteristic width
$S$
in a channel of characteristic width
![]() $h_{c}$
, the relative increase
$h_{c}$
, the relative increase
![]() ${\mathcal{R}}$
is linearly proportional to
${\mathcal{R}}$
is linearly proportional to
![]() $(S/h_{c})^{2}$
, with a proportionality factor of order unity that depends on the Schmidt number and on the frequency through the Womersley number
$(S/h_{c})^{2}$
, with a proportionality factor of order unity that depends on the Schmidt number and on the frequency through the Womersley number
![]() $\unicode[STIX]{x1D6FC}=h_{c}/(\unicode[STIX]{x1D708}/\unicode[STIX]{x1D714})^{1/2}$
(Watson Reference Watson1983; Elad, Halpern & Grotberg Reference Elad, Halpern and Grotberg1992). For the flow in the spinal canal
$\unicode[STIX]{x1D6FC}=h_{c}/(\unicode[STIX]{x1D708}/\unicode[STIX]{x1D714})^{1/2}$
(Watson Reference Watson1983; Elad, Halpern & Grotberg Reference Elad, Halpern and Grotberg1992). For the flow in the spinal canal
![]() $S\sim 1~\text{cm}$
and
$S\sim 1~\text{cm}$
and
![]() $h_{c}\sim 1~\text{mm}$
, thereby yielding
$h_{c}\sim 1~\text{mm}$
, thereby yielding
![]() ${\mathcal{R}}\sim 100$
and
${\mathcal{R}}\sim 100$
and
![]() $K\simeq 5\times 10^{-8}~\text{m}^{2}~\text{s}^{-1}$
for the effective diffusivity, with an associated enhanced diffusion velocity
$K\simeq 5\times 10^{-8}~\text{m}^{2}~\text{s}^{-1}$
for the effective diffusivity, with an associated enhanced diffusion velocity
![]() $K/L\sim 10^{-7}~\text{m}~\text{s}^{-1}$
that is about three orders of magnitude smaller than the velocities inferred from the radiological observations. In view of these estimates, it can be concluded that, although shear-enhanced diffusion contributes to the transport rate of the tracer in the spinal canal, its role will be at most secondary due to the extremely small value of the tracer molecular diffusivity. Clearly, shear-enhanced diffusion may have a more pronounced effect on the transport of lighter molecules with higher diffusivities.
$K/L\sim 10^{-7}~\text{m}~\text{s}^{-1}$
that is about three orders of magnitude smaller than the velocities inferred from the radiological observations. In view of these estimates, it can be concluded that, although shear-enhanced diffusion contributes to the transport rate of the tracer in the spinal canal, its role will be at most secondary due to the extremely small value of the tracer molecular diffusivity. Clearly, shear-enhanced diffusion may have a more pronounced effect on the transport of lighter molecules with higher diffusivities.
The previous considerations indicate that, contrary to some pervasive speculations in the neuroradiology literature (Greitz & Hannerz Reference Greitz and Hannerz1996), neither the reabsorption of CSF in the spinal canal nor the shear-enhanced diffusion of tracer markers are sufficiently efficient to produce the observed bulk motion that brings CSF downwards along the length of spinal canal and returns a portion of it back into the cranial vault with characteristic transport velocities on the order of
![]() $1~\text{cm}~\text{min}^{-1}$
. A different mechanism is postulated below to be responsible for the observed steady circulatory flow of CSF in the spinal canal, namely, the steady-streaming motion resulting from the nonlinear cumulative effects of convective acceleration (Riley Reference Riley2001), a phenomena that has already been shown to play an important role in many oscillatory flows, including respiratory and cardiovascular flows (Haselton & Scherer Reference Haselton and Scherer1980, Reference Haselton and Scherer1982; Grotberg Reference Grotberg1984; Gaver & Grotberg Reference Gaver and Grotberg1986; Padmanabhan & Pedley Reference Padmanabhan and Pedley1987; Wang & Tarbell Reference Wang and Tarbell1992; Grotberg & Jensen Reference Grotberg and Jensen2001; Sarkar & Jayaraman Reference Sarkar and Jayaraman2001; Waters & Guiot Reference Waters and Guiot2001; Muthu, Rathish Kumar & Chandra Reference Muthu, Rathish Kumar and Chandra2003; Jayaraman & Sarkar Reference Jayaraman and Sarkar2005; Ambarki et al.
Reference Ambarki, Lindqvist, Wåhlin, Petterson, Warntjes, Birgander, Malm and Eklund2012, among many others).
$1~\text{cm}~\text{min}^{-1}$
. A different mechanism is postulated below to be responsible for the observed steady circulatory flow of CSF in the spinal canal, namely, the steady-streaming motion resulting from the nonlinear cumulative effects of convective acceleration (Riley Reference Riley2001), a phenomena that has already been shown to play an important role in many oscillatory flows, including respiratory and cardiovascular flows (Haselton & Scherer Reference Haselton and Scherer1980, Reference Haselton and Scherer1982; Grotberg Reference Grotberg1984; Gaver & Grotberg Reference Gaver and Grotberg1986; Padmanabhan & Pedley Reference Padmanabhan and Pedley1987; Wang & Tarbell Reference Wang and Tarbell1992; Grotberg & Jensen Reference Grotberg and Jensen2001; Sarkar & Jayaraman Reference Sarkar and Jayaraman2001; Waters & Guiot Reference Waters and Guiot2001; Muthu, Rathish Kumar & Chandra Reference Muthu, Rathish Kumar and Chandra2003; Jayaraman & Sarkar Reference Jayaraman and Sarkar2005; Ambarki et al.
Reference Ambarki, Lindqvist, Wåhlin, Petterson, Warntjes, Birgander, Malm and Eklund2012, among many others).
In the following, we present a perturbation analysis of the flow–structure interaction problem responsible for the motion of CSF in the spinal canal. Our analysis takes advantage of the disparity of scales associated with the geometry of the subarachnoid space, which is modelled as a thin annular canal with slowly changing properties, and also of the limited compliance of the dura membrane bounding the CSF, whose small deformations are measured by a small asymptotic parameter
![]() $\unicode[STIX]{x1D700}$
, on the order of the ratio
$\unicode[STIX]{x1D700}$
, on the order of the ratio
![]() $\unicode[STIX]{x0394}V/V\ll 1$
of the tidal volume to the total CSF volume inside the spinal canal. At leading order in the limit
$\unicode[STIX]{x0394}V/V\ll 1$
of the tidal volume to the total CSF volume inside the spinal canal. At leading order in the limit
![]() $\unicode[STIX]{x1D700}\ll 1$
, we find an unsteady lubrication problem that generates an oscillatory flow with axial velocities that decrease monotonically along the length of the canal. More importantly, we show that the nonlinear terms associated with the convective acceleration, negligible at leading order, yield first-order corrections that include a steady-streaming component, corresponding to a bulk recirculating motion of the CSF along the length of the canal, with characteristic velocities that are a factor
$\unicode[STIX]{x1D700}\ll 1$
, we find an unsteady lubrication problem that generates an oscillatory flow with axial velocities that decrease monotonically along the length of the canal. More importantly, we show that the nonlinear terms associated with the convective acceleration, negligible at leading order, yield first-order corrections that include a steady-streaming component, corresponding to a bulk recirculating motion of the CSF along the length of the canal, with characteristic velocities that are a factor
![]() $\unicode[STIX]{x1D700}$
smaller than those of the leading-order oscillatory flow. We applied our general asymptotic formulation to a canonical configuration consisting of a slender compliant cylindrical pipe with a coaxial cylindrical inclusion that is closed at the distal end and subjected to small periodic pressure pulsations at its open entrance. The results of the analysis of this idealized geometry of the spinal canal are shown to be in agreement not only with experimental measurements conducted in a in-vitro model but also to be consistent with radiological measurements in human adults.
$\unicode[STIX]{x1D700}$
smaller than those of the leading-order oscillatory flow. We applied our general asymptotic formulation to a canonical configuration consisting of a slender compliant cylindrical pipe with a coaxial cylindrical inclusion that is closed at the distal end and subjected to small periodic pressure pulsations at its open entrance. The results of the analysis of this idealized geometry of the spinal canal are shown to be in agreement not only with experimental measurements conducted in a in-vitro model but also to be consistent with radiological measurements in human adults.
2 CSF motion in the spinal canal
2.1 Geometrical considerations
In analyzing the motion of CSF, the spinal SAS will be modelled as a thin annular gap of length
![]() $L$
whose cross-section varies slowly between the base of the cranial cavity and the lumbar region. The orthogonal curvilinear coordinates
$L$
whose cross-section varies slowly between the base of the cranial cavity and the lumbar region. The orthogonal curvilinear coordinates
![]() $(x,y,s)$
shown in the lower inset of figure 1 will be employed in the analysis, with
$(x,y,s)$
shown in the lower inset of figure 1 will be employed in the analysis, with
![]() $x$
denoting the distance from the canal entrance measured along the spinal cord,
$x$
denoting the distance from the canal entrance measured along the spinal cord,
![]() $y$
being the normal distance to the pia mater (the inner surface), and
$y$
being the normal distance to the pia mater (the inner surface), and
![]() $s$
being the distance measured from the symmetry plane around the surface of the pia mater normalized with the spinal–cord perimeter
$s$
being the distance measured from the symmetry plane around the surface of the pia mater normalized with the spinal–cord perimeter
![]() $\ell (x)$
. The values of the coordinates are in the ranges
$\ell (x)$
. The values of the coordinates are in the ranges
![]() $0\leqslant x\leqslant L$
,
$0\leqslant x\leqslant L$
,
![]() $0\leqslant y\leqslant h(x,s,t)$
and
$0\leqslant y\leqslant h(x,s,t)$
and
![]() $0\leqslant s\leqslant 1$
, where
$0\leqslant s\leqslant 1$
, where
![]() $h(x,s,t)$
is the canal width. Characteristic values of
$h(x,s,t)$
is the canal width. Characteristic values of
![]() $h$
and
$h$
and
![]() $\ell$
are
$\ell$
are
![]() $h_{c}\sim 0.1~\text{cm}$
and
$h_{c}\sim 0.1~\text{cm}$
and
![]() $\ell _{c}\sim 2~\text{cm}$
, respectively, while
$\ell _{c}\sim 2~\text{cm}$
, respectively, while
![]() $L\sim 60{-}80~\text{cm}$
, resulting in the inequalities
$L\sim 60{-}80~\text{cm}$
, resulting in the inequalities
which are to be used in simplifying the description, as shown below.
The conservation equation in terms of the curvilinear coordinates
![]() $(x,y,s)$
can be written following the general expressions given in Batchelor (Reference Batchelor2000). In particular, when the condition (2.1) is accounted for, the continuity equation takes the simplified form
$(x,y,s)$
can be written following the general expressions given in Batchelor (Reference Batchelor2000). In particular, when the condition (2.1) is accounted for, the continuity equation takes the simplified form
where
![]() $u$
,
$u$
,
![]() $v$
and
$v$
and
![]() $w$
are the velocity components in the
$w$
are the velocity components in the
![]() $x$
,
$x$
,
![]() $y$
and
$y$
and
![]() $s$
directions, respectively. A straightforward order-of-magnitude balance of (2.2) provides
$s$
directions, respectively. A straightforward order-of-magnitude balance of (2.2) provides
relating the characteristic values
![]() $u_{c}$
,
$u_{c}$
,
![]() $v_{c}$
and
$v_{c}$
and
![]() $w_{c}$
of the three velocity components. These scalings correspond to streamlines aligned in the
$w_{c}$
of the three velocity components. These scalings correspond to streamlines aligned in the
![]() $x$
direction (i.e.
$x$
direction (i.e.
![]() $u\sim (L/\ell _{c})w\gg w$
) with an accompanying slow transverse motion occurring predominantly in the azimuthal direction with
$u\sim (L/\ell _{c})w\gg w$
) with an accompanying slow transverse motion occurring predominantly in the azimuthal direction with
![]() $w\sim (\ell _{c}/h_{c})v\gg v$
, with
$w\sim (\ell _{c}/h_{c})v\gg v$
, with
![]() $v$
being the smallest velocity component.
$v$
being the smallest velocity component.
In the resulting slender flow, the characteristic values of the spatial pressure differences needed to establish the motion in the
![]() $x$
,
$x$
,
![]() $y$
and
$y$
and
![]() $s$
directions are given by
$s$
directions are given by
![]() $\unicode[STIX]{x1D6FF}_{x}p=\unicode[STIX]{x1D70C}\unicode[STIX]{x1D714}u_{c}L$
,
$\unicode[STIX]{x1D6FF}_{x}p=\unicode[STIX]{x1D70C}\unicode[STIX]{x1D714}u_{c}L$
,
![]() $\unicode[STIX]{x1D6FF}_{y}p=\unicode[STIX]{x1D70C}\unicode[STIX]{x1D714}v_{c}h_{c}$
and
$\unicode[STIX]{x1D6FF}_{y}p=\unicode[STIX]{x1D70C}\unicode[STIX]{x1D714}v_{c}h_{c}$
and
![]() $\unicode[STIX]{x1D6FF}_{s}p=\unicode[STIX]{x1D70C}\unicode[STIX]{x1D714}w_{c}\ell _{c}$
, respectively, as follows from a balance between the pressure gradient and the local acceleration. These values are very different in magnitude, as can be seen by using (2.3), yielding
$\unicode[STIX]{x1D6FF}_{s}p=\unicode[STIX]{x1D70C}\unicode[STIX]{x1D714}w_{c}\ell _{c}$
, respectively, as follows from a balance between the pressure gradient and the local acceleration. These values are very different in magnitude, as can be seen by using (2.3), yielding
The scalings (2.4) can be taken into account when describing the variations of the pressure
![]() $p$
from the entrance value
$p$
from the entrance value
![]() $p_{c}$
. Neglecting the small contribution to the pressure fluctuation associated with breathing, the value of
$p_{c}$
. Neglecting the small contribution to the pressure fluctuation associated with breathing, the value of
![]() $p_{c}$
can be written as
$p_{c}$
can be written as
where
![]() $p_{o}$
is the time-averaged intracranial pressure,
$p_{o}$
is the time-averaged intracranial pressure,
![]() $(\unicode[STIX]{x0394}p)_{c}$
is the amplitude of the cranial pressure pulse, and
$(\unicode[STIX]{x0394}p)_{c}$
is the amplitude of the cranial pressure pulse, and
![]() $\unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D714}t)$
is a dimensionless periodic function with angular frequency
$\unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D714}t)$
is a dimensionless periodic function with angular frequency
![]() $\unicode[STIX]{x1D714}\simeq 2\unicode[STIX]{x03C0}$
Hz, associated with the cardiac cycle. According to (2.4), with small errors of order
$\unicode[STIX]{x1D714}\simeq 2\unicode[STIX]{x03C0}$
Hz, associated with the cardiac cycle. According to (2.4), with small errors of order
![]() $(h_{c}/\ell _{c})^{2}$
one may neglect the pressure variations in the
$(h_{c}/\ell _{c})^{2}$
one may neglect the pressure variations in the
![]() $y$
direction when writing
$y$
direction when writing
for the pressure variation along the canal, with
![]() $p^{\prime }(x,t)$
denoting the value of the pressure difference
$p^{\prime }(x,t)$
denoting the value of the pressure difference
![]() $p-p_{c}(t)$
along the curve
$p-p_{c}(t)$
along the curve
![]() $s=y=0$
. The term
$s=y=0$
. The term
![]() $\tilde{p}\sim (\ell _{c}/L)^{2}p^{\prime }\ll p^{\prime }$
, measuring the small pressure differences around the canal, must be included to describe the azimuthal motion.
$\tilde{p}\sim (\ell _{c}/L)^{2}p^{\prime }\ll p^{\prime }$
, measuring the small pressure differences around the canal, must be included to describe the azimuthal motion.
2.2 Constitutive equation and elastic parameters
The dura membrane deforms in response to the local pressure variations to accommodate the inflow and outflow of CSF into the canal, so that the canal width
![]() $h(x,s,t)$
is a function of time that must be determined as part of the solution. The deformations
$h(x,s,t)$
is a function of time that must be determined as part of the solution. The deformations
![]() $h^{\prime }=h-h_{o}$
are to be defined relative to the unperturbed width distribution
$h^{\prime }=h-h_{o}$
are to be defined relative to the unperturbed width distribution
![]() $h_{o}(x,s)$
describing the geometry of the canal when the pressure everywhere is uniform and equal to
$h_{o}(x,s)$
describing the geometry of the canal when the pressure everywhere is uniform and equal to
![]() $p=p_{o}$
, with
$p=p_{o}$
, with
![]() $A_{o}(x)=\ell (x)\,\int _{0}^{1}h_{o}(x,s)\,\text{d}s$
representing the unperturbed value of the cross-sectional area. Since the tidal volume is small compared with the total volume of CSF, the associated changes in the shape of the canal must satisfy
$A_{o}(x)=\ell (x)\,\int _{0}^{1}h_{o}(x,s)\,\text{d}s$
representing the unperturbed value of the cross-sectional area. Since the tidal volume is small compared with the total volume of CSF, the associated changes in the shape of the canal must satisfy
The description of the coupling between the fluid motion and the deformation of the dura membrane in general amounts to a very complicated fluid–structure interaction problem. A simplified solution is pursued below on the basis of the presumed linear relation
![]() $h^{\prime }\propto (p-p_{o})$
. The description accounts also for the fact that the pressure at a given canal section is nearly uniform, with small relative variations, represented in (2.6) by the term
$h^{\prime }\propto (p-p_{o})$
. The description accounts also for the fact that the pressure at a given canal section is nearly uniform, with small relative variations, represented in (2.6) by the term
![]() $\tilde{p}$
, that are of order
$\tilde{p}$
, that are of order
![]() $(\ell _{c}/L)^{2}$
. If these are neglected, then one may write
$(\ell _{c}/L)^{2}$
. If these are neglected, then one may write
![]() $p-p_{o}\simeq (\unicode[STIX]{x0394}p)_{c}\unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D714}t)+p^{\prime }(x,t)$
, which, together with the additional assumption that the elastic properties of the dura membrane are independent of
$p-p_{o}\simeq (\unicode[STIX]{x0394}p)_{c}\unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D714}t)+p^{\prime }(x,t)$
, which, together with the additional assumption that the elastic properties of the dura membrane are independent of
![]() $s$
, yields the simplified constitutive equation
$s$
, yields the simplified constitutive equation
In writing (2.8) we have chosen to scale the deformation with the average canal width
![]() $A_{o}/\ell \sim h_{c}$
and include for generality an effective elastic modulus
$A_{o}/\ell \sim h_{c}$
and include for generality an effective elastic modulus
![]() $E_{e}(x)$
, the latter embodying the overall effect of different microanatomical features such as the distribution of veins and fatty epidural tissue in the dura membrane. Variations of the elastic properties of the dura membrane at a given section, not considered in the present development, could be incorporated in the model by allowing the effective elastic modulus
$E_{e}(x)$
, the latter embodying the overall effect of different microanatomical features such as the distribution of veins and fatty epidural tissue in the dura membrane. Variations of the elastic properties of the dura membrane at a given section, not considered in the present development, could be incorporated in the model by allowing the effective elastic modulus
![]() $E_{e}$
to be a function of
$E_{e}$
to be a function of
![]() $s$
, resulting in the local deformation
$s$
, resulting in the local deformation
![]() $h^{\prime }$
being also a function of
$h^{\prime }$
being also a function of
![]() $s$
, according to (2.8).
$s$
, according to (2.8).
According to (2.7) and (2.8) the value of
![]() $E_{e}$
must be much larger than
$E_{e}$
must be much larger than
![]() $p-p_{o}$
, so that the resulting deformations remain small according to
$p-p_{o}$
, so that the resulting deformations remain small according to
![]() $(p-p_{o})/E_{e}\sim \unicode[STIX]{x0394}V/V\ll 1$
. The ratio of the characteristic value of the local pressure variation
$(p-p_{o})/E_{e}\sim \unicode[STIX]{x0394}V/V\ll 1$
. The ratio of the characteristic value of the local pressure variation
![]() $p-p_{o}\sim (\unicode[STIX]{x0394}p)_{c}$
to the characteristic value
$p-p_{o}\sim (\unicode[STIX]{x0394}p)_{c}$
to the characteristic value
![]() $E_{c}$
of
$E_{c}$
of
![]() $E_{e}$
defines the small parameter
$E_{e}$
defines the small parameter
to be used in the following description as a measure of the compliance.
The effective elastic modulus
![]() $E_{e}$
determines the wave speed
$E_{e}$
determines the wave speed
![]() $(E_{e}/\unicode[STIX]{x1D70C})^{1/2}$
of the resulting pulsatile motion along the canal. Noninvasive measurements (Kalata et al.
Reference Kalata, Martin, Oshinski, Jerosch-Herold, Royston and Loth2009) using MRI have shown this wave speed to be on the order of a few metres per second, giving associated wavelengths
$(E_{e}/\unicode[STIX]{x1D70C})^{1/2}$
of the resulting pulsatile motion along the canal. Noninvasive measurements (Kalata et al.
Reference Kalata, Martin, Oshinski, Jerosch-Herold, Royston and Loth2009) using MRI have shown this wave speed to be on the order of a few metres per second, giving associated wavelengths
![]() $(E_{c}/\unicode[STIX]{x1D70C})^{1/2}/\unicode[STIX]{x1D714}$
that are comparable to the canal length
$(E_{c}/\unicode[STIX]{x1D70C})^{1/2}/\unicode[STIX]{x1D714}$
that are comparable to the canal length
![]() $L$
. Correspondingly, the ratio
$L$
. Correspondingly, the ratio
defines a dimensionless elastic wavenumber of order unity, another important parameter in the description below.
2.3 Simplified conservation equations
We give below the equations that determine the velocity, whose
![]() $x$
,
$x$
,
![]() $y$
and
$y$
and
![]() $s$
components,
$s$
components,
![]() $u(x,y,s,t)$
,
$u(x,y,s,t)$
,
![]() $v(x,y,s,t)$
and
$v(x,y,s,t)$
and
![]() $w(x,y,s,t)$
, must satisfy the non-slip boundary conditions
$w(x,y,s,t)$
, must satisfy the non-slip boundary conditions
![]() $u=v=w=0$
at
$u=v=w=0$
at
![]() $y=0$
and
$y=0$
and
![]() $u=v-\unicode[STIX]{x2202}h^{\prime }/\unicode[STIX]{x2202}t=w=0$
at
$u=v-\unicode[STIX]{x2202}h^{\prime }/\unicode[STIX]{x2202}t=w=0$
at
![]() $y=h(x,s,t)$
. The problem also involves the displacement
$y=h(x,s,t)$
. The problem also involves the displacement
![]() $h^{\prime }(x,t)=h-h_{o}(x,s)$
, and the pressure field, described in terms of the functions
$h^{\prime }(x,t)=h-h_{o}(x,s)$
, and the pressure field, described in terms of the functions
![]() $p^{\prime }(x,t)$
and
$p^{\prime }(x,t)$
and
![]() $\tilde{p}(x,s,t)$
.
$\tilde{p}(x,s,t)$
.
The computation of
![]() $u$
and
$u$
and
![]() $w$
requires consideration of the
$w$
requires consideration of the
![]() $x$
and
$x$
and
![]() $s$
components of the momentum equation, which can be written for the curvilinear coordinates defined above by neglecting terms of order
$s$
components of the momentum equation, which can be written for the curvilinear coordinates defined above by neglecting terms of order
![]() $(\ell _{c}/L)^{2}$
or
$(\ell _{c}/L)^{2}$
or
![]() $(h_{c}/\ell _{c})^{2}$
(or smaller) to give
$(h_{c}/\ell _{c})^{2}$
(or smaller) to give
whereas the
![]() $y$
component of the momentum equation, which would be needed to compute the small spatial pressure differences
$y$
component of the momentum equation, which would be needed to compute the small spatial pressure differences
![]() $\unicode[STIX]{x1D6FF}_{y}p$
, can be omitted in the slender-flow approximation at the order considered here. At the same level of approximation, the viscous terms have been simplified in (2.11) and (2.12) by discarding the terms involving
$\unicode[STIX]{x1D6FF}_{y}p$
, can be omitted in the slender-flow approximation at the order considered here. At the same level of approximation, the viscous terms have been simplified in (2.11) and (2.12) by discarding the terms involving
![]() $\unicode[STIX]{x2202}^{2}/\unicode[STIX]{x2202}x^{2}$
and
$\unicode[STIX]{x2202}^{2}/\unicode[STIX]{x2202}x^{2}$
and
![]() $\unicode[STIX]{x2202}^{2}/\unicode[STIX]{x2202}s^{2}$
, which are smaller than the terms that have been retained by a factor
$\unicode[STIX]{x2202}^{2}/\unicode[STIX]{x2202}s^{2}$
, which are smaller than the terms that have been retained by a factor
![]() $(h_{c}/L)^{2}$
and
$(h_{c}/L)^{2}$
and
![]() $(h_{c}/\ell _{c})^{2}$
, respectively.
$(h_{c}/\ell _{c})^{2}$
, respectively.
The transverse velocity component
![]() $v$
can be evaluated in terms of
$v$
can be evaluated in terms of
![]() $u$
and
$u$
and
![]() $w$
from
$w$
from
involving the dummy integration variable
![]() ${\tilde{y}}$
. The above equation is obtained by integrating the continuity equation (2.2) in the
${\tilde{y}}$
. The above equation is obtained by integrating the continuity equation (2.2) in the
![]() $y$
direction with the condition
$y$
direction with the condition
![]() $u=v=w=0$
at
$u=v=w=0$
at
![]() $y=0$
. Evaluating the above equation at
$y=0$
. Evaluating the above equation at
![]() $y=h$
gives
$y=h$
gives
which is the corresponding Reynolds lubrication equation for the problem.
Further integrations of the continuity equation also become useful in the development, which assumes that the spinal canal is symmetric, such that
![]() $h_{o}(x,s)=h_{o}(x,1-s)$
, resulting in the conditions
$h_{o}(x,s)=h_{o}(x,1-s)$
, resulting in the conditions
![]() $\int _{0}^{h}w\,\text{d}y=0$
at
$\int _{0}^{h}w\,\text{d}y=0$
at
![]() $s=0$
and at
$s=0$
and at
![]() $s=1/2$
. Multiplying (2.14) by
$s=1/2$
. Multiplying (2.14) by
![]() $\text{d}s$
and integrating between
$\text{d}s$
and integrating between
![]() $0$
and
$0$
and
![]() $s$
provides
$s$
provides
after using the symmetry condition
![]() $\int _{0}^{h}w\,\text{d}y=0$
at
$\int _{0}^{h}w\,\text{d}y=0$
at
![]() $s=0$
, whereas the condition
$s=0$
, whereas the condition
![]() $\int _{0}^{h}w\,\text{d}y=0$
at
$\int _{0}^{h}w\,\text{d}y=0$
at
![]() $s=1/2$
(or
$s=1/2$
(or
![]() $s=1$
) yields
$s=1$
) yields
The displacement
![]() $h^{\prime }$
is related to the local pressure
$h^{\prime }$
is related to the local pressure
![]() $p-p_{o}\simeq (\unicode[STIX]{x0394}p)_{c}\unicode[STIX]{x1D6F1}+p^{\prime }$
by the constitutive equation (2.8), which can be differentiated with respect to time to give
$p-p_{o}\simeq (\unicode[STIX]{x0394}p)_{c}\unicode[STIX]{x1D6F1}+p^{\prime }$
by the constitutive equation (2.8), which can be differentiated with respect to time to give
The additional equation
obtained by combining (2.16) and (2.17) will be found below to be useful in computing
![]() $p^{\prime }$
as a function of the streamwise velocity
$p^{\prime }$
as a function of the streamwise velocity
![]() $u$
.
$u$
.
2.4 Dimensionless formulation
An order-of-magnitude analysis provides the characteristic scales for the problem. The development begins by using (2.18) with
![]() $(\unicode[STIX]{x0394}p)_{c}/E_{e}\sim \unicode[STIX]{x1D700}$
to provide
$(\unicode[STIX]{x0394}p)_{c}/E_{e}\sim \unicode[STIX]{x1D700}$
to provide
![]() $u_{c}=\unicode[STIX]{x1D700}L\unicode[STIX]{x1D714}$
as an estimate for the characteristic value of
$u_{c}=\unicode[STIX]{x1D700}L\unicode[STIX]{x1D714}$
as an estimate for the characteristic value of
![]() $u$
, on the order of a few centimetres per second, as can be seen by using
$u$
, on the order of a few centimetres per second, as can be seen by using
![]() $\unicode[STIX]{x1D700}\sim \unicode[STIX]{x0394}V/V\sim 0.02$
,
$\unicode[STIX]{x1D700}\sim \unicode[STIX]{x0394}V/V\sim 0.02$
,
![]() $\unicode[STIX]{x1D714}=2\unicode[STIX]{x03C0}$
and
$\unicode[STIX]{x1D714}=2\unicode[STIX]{x03C0}$
and
![]() $L\sim 60{-}80~\text{cm}$
. The characteristic values
$L\sim 60{-}80~\text{cm}$
. The characteristic values
![]() $w_{c}=\unicode[STIX]{x1D700}\ell _{c}\unicode[STIX]{x1D714}$
and
$w_{c}=\unicode[STIX]{x1D700}\ell _{c}\unicode[STIX]{x1D714}$
and
![]() $v_{c}=\unicode[STIX]{x1D700}h_{c}\unicode[STIX]{x1D714}$
follow from (2.3). The spatial pressure changes needed to move the fluid can be estimated from the balance between the local acceleration and the pressure gradient in (2.11) and (2.12) to give
$v_{c}=\unicode[STIX]{x1D700}h_{c}\unicode[STIX]{x1D714}$
follow from (2.3). The spatial pressure changes needed to move the fluid can be estimated from the balance between the local acceleration and the pressure gradient in (2.11) and (2.12) to give
![]() $\unicode[STIX]{x1D6FF}_{x}p=\unicode[STIX]{x1D70C}\unicode[STIX]{x1D700}(\unicode[STIX]{x1D714}L)^{2}$
and
$\unicode[STIX]{x1D6FF}_{x}p=\unicode[STIX]{x1D70C}\unicode[STIX]{x1D700}(\unicode[STIX]{x1D714}L)^{2}$
and
![]() $\unicode[STIX]{x1D6FF}_{s}p=\unicode[STIX]{x1D70C}\unicode[STIX]{x1D700}(\unicode[STIX]{x1D714}\ell _{c})^{2}$
. Additional order-of-magnitude balances in these two equations reveal that the convective acceleration is smaller than the local acceleration by a factor
$\unicode[STIX]{x1D6FF}_{s}p=\unicode[STIX]{x1D70C}\unicode[STIX]{x1D700}(\unicode[STIX]{x1D714}\ell _{c})^{2}$
. Additional order-of-magnitude balances in these two equations reveal that the convective acceleration is smaller than the local acceleration by a factor
![]() $\unicode[STIX]{x1D700}$
, whereas the comparison between the local acceleration and the viscous force yields
$\unicode[STIX]{x1D700}$
, whereas the comparison between the local acceleration and the viscous force yields
where
is the Womersley number of the flow (the reciprocal of the square root of the relevant Stokes number
![]() $\unicode[STIX]{x1D708}/(h_{c}^{2}\unicode[STIX]{x1D714})$
), typically of order unity, as can be seen by using
$\unicode[STIX]{x1D708}/(h_{c}^{2}\unicode[STIX]{x1D714})$
), typically of order unity, as can be seen by using
![]() $h_{c}\sim 10^{-3}~\text{m}$
,
$h_{c}\sim 10^{-3}~\text{m}$
,
![]() $\unicode[STIX]{x1D714}=2\unicode[STIX]{x03C0}~\text{ s}^{-1}$
and
$\unicode[STIX]{x1D714}=2\unicode[STIX]{x03C0}~\text{ s}^{-1}$
and
![]() $\unicode[STIX]{x1D708}\sim 10^{-6}~\text{m}^{2}~\text{s}^{-1}$
.
$\unicode[STIX]{x1D708}\sim 10^{-6}~\text{m}^{2}~\text{s}^{-1}$
.
The relative scalings discussed above become clear when writing the above problem in dimensionless form by introduction of the dimensionless variables
![]() $u^{\ast }=u/u_{c}$
,
$u^{\ast }=u/u_{c}$
,
![]() $v^{\ast }=v/v_{c}$
,
$v^{\ast }=v/v_{c}$
,
![]() $w^{\ast }=w/w_{c}$
,
$w^{\ast }=w/w_{c}$
,
![]() $p^{\prime \ast }=p^{\prime }/\unicode[STIX]{x1D6FF}_{x}p$
,
$p^{\prime \ast }=p^{\prime }/\unicode[STIX]{x1D6FF}_{x}p$
,
![]() $\tilde{p}^{\ast }=\tilde{p}/\unicode[STIX]{x1D6FF}_{s}p$
,
$\tilde{p}^{\ast }=\tilde{p}/\unicode[STIX]{x1D6FF}_{s}p$
,
![]() $t^{\ast }=\unicode[STIX]{x1D714}t$
,
$t^{\ast }=\unicode[STIX]{x1D714}t$
,
![]() $x^{\ast }=x/L$
,
$x^{\ast }=x/L$
,
![]() $\ell ^{\ast }=\ell /\ell _{c}$
,
$\ell ^{\ast }=\ell /\ell _{c}$
,
![]() $h_{o}^{\ast }=h_{o}/h_{c}$
,
$h_{o}^{\ast }=h_{o}/h_{c}$
,
![]() $h^{\ast }=h/h_{c}$
,
$h^{\ast }=h/h_{c}$
,
![]() $h^{\prime \ast }=(h-h_{o})/(\unicode[STIX]{x1D700}h_{c})$
,
$h^{\prime \ast }=(h-h_{o})/(\unicode[STIX]{x1D700}h_{c})$
,
![]() $A_{o}^{\ast }=A_{o}/(\ell _{c}h_{c})$
and
$A_{o}^{\ast }=A_{o}/(\ell _{c}h_{c})$
and
![]() $E_{e}^{\ast }=E_{e}/E_{c}$
. In addition, to facilitate the description of the temporal changes of the canal width it is convenient to scale the distance
$E_{e}^{\ast }=E_{e}/E_{c}$
. In addition, to facilitate the description of the temporal changes of the canal width it is convenient to scale the distance
![]() $y$
with the local width
$y$
with the local width
![]() $h(x,s,t)$
through the normalized coordinate
$h(x,s,t)$
through the normalized coordinate
![]() $\unicode[STIX]{x1D702}=y/h(x,s,t)$
. In what follows, the asterisks used to denote dimensionless variables will be dropped to simplify the notation.
$\unicode[STIX]{x1D702}=y/h(x,s,t)$
. In what follows, the asterisks used to denote dimensionless variables will be dropped to simplify the notation.
Since we have a total of six unknowns (i.e.
![]() $u$
,
$u$
,
![]() $v$
,
$v$
,
![]() $w$
,
$w$
,
![]() $p^{\prime }$
,
$p^{\prime }$
,
![]() $\tilde{p}$
and
$\tilde{p}$
and
![]() $h^{\prime }$
, with
$h^{\prime }$
, with
![]() $h=h_{o}+\unicode[STIX]{x1D700}h^{\prime }$
) the description requires in principle six equations, which are given below in dimensionless form. We begin by writing (2.11) and (2.12) as
$h=h_{o}+\unicode[STIX]{x1D700}h^{\prime }$
) the description requires in principle six equations, which are given below in dimensionless form. We begin by writing (2.11) and (2.12) as
where
and
 $$\begin{eqnarray}\displaystyle F_{s} & = & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}(uw)+2\frac{uw}{\ell }\frac{\unicode[STIX]{x2202}\ell }{\unicode[STIX]{x2202}x}+\frac{1}{h}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}(vw)+\frac{1}{\ell }\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}s}(w^{2})-\frac{\unicode[STIX]{x2202}h^{\prime }}{\unicode[STIX]{x2202}t}\frac{\unicode[STIX]{x1D702}}{h}\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}x}\frac{\unicode[STIX]{x1D702}}{h}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}(uw)-\frac{1}{\ell }\frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}s}\frac{\unicode[STIX]{x1D702}}{h}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}(w^{2})\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{s} & = & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}(uw)+2\frac{uw}{\ell }\frac{\unicode[STIX]{x2202}\ell }{\unicode[STIX]{x2202}x}+\frac{1}{h}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}(vw)+\frac{1}{\ell }\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}s}(w^{2})-\frac{\unicode[STIX]{x2202}h^{\prime }}{\unicode[STIX]{x2202}t}\frac{\unicode[STIX]{x1D702}}{h}\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}x}\frac{\unicode[STIX]{x1D702}}{h}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}(uw)-\frac{1}{\ell }\frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}s}\frac{\unicode[STIX]{x1D702}}{h}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}(w^{2})\end{eqnarray}$$
represent the convective terms, including the apparent convection associated with
![]() $\unicode[STIX]{x2202}h^{\prime }/\unicode[STIX]{x2202}t$
. The streamwise pressure variation
$\unicode[STIX]{x2202}h^{\prime }/\unicode[STIX]{x2202}t$
. The streamwise pressure variation
![]() $p^{\prime }$
is related to the volume flux by (2.18), which can be written as
$p^{\prime }$
is related to the volume flux by (2.18), which can be written as
whereas the deformation
![]() $h^{\prime }$
satisfies
$h^{\prime }$
satisfies
as obtained from (2.17). The transverse velocity component
![]() $v$
can be evaluated from (2.13) in terms of
$v$
can be evaluated from (2.13) in terms of
![]() $u$
and
$u$
and
![]() $w$
to yield
$w$
to yield
Finally, the integral continuity balance
obtained by combining (2.15) and (2.16), will be useful in computing the azimuthal variation of the pressure
![]() $\tilde{p}$
.
$\tilde{p}$
.
The velocity components
![]() $u$
and
$u$
and
![]() $w$
must satisfy the non-slip boundary conditions
$w$
must satisfy the non-slip boundary conditions
![]() $u=w=0$
at
$u=w=0$
at
![]() $\unicode[STIX]{x1D702}=0,1$
. At the canal entrance the pressure is
$\unicode[STIX]{x1D702}=0,1$
. At the canal entrance the pressure is
![]() $p=p_{c}(t)$
, resulting in the condition
$p=p_{c}(t)$
, resulting in the condition
Also, the streamwise volume flux must vanish at the closed end of the canal, so that
Besides the Womersley number
![]() $\unicode[STIX]{x1D6FC}$
defined in (2.20) and the dimensionless elastic wavenumber
$\unicode[STIX]{x1D6FC}$
defined in (2.20) and the dimensionless elastic wavenumber
![]() $k$
defined in (2.10), both of order unity, the above problem depends on the elasticity parameter
$k$
defined in (2.10), both of order unity, the above problem depends on the elasticity parameter
![]() $\unicode[STIX]{x1D700}\ll 1$
, identified earlier in (2.9), with
$\unicode[STIX]{x1D700}\ll 1$
, identified earlier in (2.9), with
![]() $\unicode[STIX]{x1D6FC}^{2}\unicode[STIX]{x1D700}\ll 1$
representing the relevant Reynolds number for the flow. As can be seen in (2.21) and (2.22), at leading order in the limit
$\unicode[STIX]{x1D6FC}^{2}\unicode[STIX]{x1D700}\ll 1$
representing the relevant Reynolds number for the flow. As can be seen in (2.21) and (2.22), at leading order in the limit
![]() $\unicode[STIX]{x1D700}\ll 1$
the flow in the thin canal corresponds to an oscillatory lubrication problem, where the motion is determined by a balance between the local acceleration, the pressure gradient, and the viscous forces associated with the transverse velocity derivatives.
$\unicode[STIX]{x1D700}\ll 1$
the flow in the thin canal corresponds to an oscillatory lubrication problem, where the motion is determined by a balance between the local acceleration, the pressure gradient, and the viscous forces associated with the transverse velocity derivatives.
3 Leading-order oscillatory flow
The solution can be obtained using perturbation analysis by introducing expansions for the different flow variables of the form
![]() $u=u_{0}+\unicode[STIX]{x1D700}u_{1}+\cdots \,,v=v_{0}+\unicode[STIX]{x1D700}v_{1}+\cdots \,,w=w_{0}+\unicode[STIX]{x1D700}w_{1}+\cdots \,,p^{\prime }=p_{0}^{\prime }+\unicode[STIX]{x1D700}p_{1}^{\prime }+\cdots \,$
and
$u=u_{0}+\unicode[STIX]{x1D700}u_{1}+\cdots \,,v=v_{0}+\unicode[STIX]{x1D700}v_{1}+\cdots \,,w=w_{0}+\unicode[STIX]{x1D700}w_{1}+\cdots \,,p^{\prime }=p_{0}^{\prime }+\unicode[STIX]{x1D700}p_{1}^{\prime }+\cdots \,$
and
![]() $\tilde{p}=\tilde{p}_{0}+\unicode[STIX]{x1D700}\tilde{p}_{1}+\cdots \,,$
together with the expansion
$\tilde{p}=\tilde{p}_{0}+\unicode[STIX]{x1D700}\tilde{p}_{1}+\cdots \,,$
together with the expansion
![]() $h^{\prime }(x,t)=(h-h_{o})/\unicode[STIX]{x1D700}=h_{0}^{\prime }+\unicode[STIX]{x1D700}h_{1}^{\prime }+\cdots \,$
for the deformation of the canal. It will be seen that the leading-order solution is purely oscillatory, whereas the corrections include a steady component corresponding to the steady bulk-flow motion, with characteristic velocities of order
$h^{\prime }(x,t)=(h-h_{o})/\unicode[STIX]{x1D700}=h_{0}^{\prime }+\unicode[STIX]{x1D700}h_{1}^{\prime }+\cdots \,$
for the deformation of the canal. It will be seen that the leading-order solution is purely oscillatory, whereas the corrections include a steady component corresponding to the steady bulk-flow motion, with characteristic velocities of order
![]() $\unicode[STIX]{x1D700}u_{c}=\unicode[STIX]{x1D700}^{2}\unicode[STIX]{x1D714}L$
(i.e. a few centimetres per minute, in agreement with the observed transport rates in the spinal canal).
$\unicode[STIX]{x1D700}u_{c}=\unicode[STIX]{x1D700}^{2}\unicode[STIX]{x1D714}L$
(i.e. a few centimetres per minute, in agreement with the observed transport rates in the spinal canal).
At leading order, (2.21), (2.22), and (2.25)–(2.28) reduce to the linear equations
The solution depends on the shape of the canal through the known functions
![]() $h_{o}(x,s)$
and
$h_{o}(x,s)$
and
![]() $\ell (x)$
, on its elastic properties through the function
$\ell (x)$
, on its elastic properties through the function
![]() $E_{e}(x)$
, and on the temporal variation of the intracranial pressure, defined by the periodic function
$E_{e}(x)$
, and on the temporal variation of the intracranial pressure, defined by the periodic function
![]() $\unicode[STIX]{x1D6F1}(t)$
.
$\unicode[STIX]{x1D6F1}(t)$
.
An analytic solution can be obtained for the case of a harmonic intracranial pressure
![]() $\unicode[STIX]{x1D6F1}(t)=\cos t$
by introducing the complex functions
$\unicode[STIX]{x1D6F1}(t)=\cos t$
by introducing the complex functions
![]() $U(x,\unicode[STIX]{x1D702},s)$
,
$U(x,\unicode[STIX]{x1D702},s)$
,
![]() $V(x,\unicode[STIX]{x1D702},s)$
,
$V(x,\unicode[STIX]{x1D702},s)$
,
![]() $W(x,\unicode[STIX]{x1D702},s)$
,
$W(x,\unicode[STIX]{x1D702},s)$
,
![]() $P^{\prime }(x)$
,
$P^{\prime }(x)$
,
![]() $\tilde{P}(x,s)$
and
$\tilde{P}(x,s)$
and
![]() $H^{\prime }(x)$
defined such that
$H^{\prime }(x)$
defined such that
The functions
with
 $$\begin{eqnarray}G(x,\unicode[STIX]{x1D702},s)=1-\frac{\cosh \left[{\displaystyle \frac{\unicode[STIX]{x1D6FC}h_{o}}{2}}{\displaystyle \frac{1+\text{i}}{\sqrt{2}}}\left(2\unicode[STIX]{x1D702}-1\right)\right]}{\cosh \left[{\displaystyle \frac{\unicode[STIX]{x1D6FC}h_{o}}{2}}{\displaystyle \frac{1+\text{i}}{\sqrt{2}}}\right]}\end{eqnarray}$$
$$\begin{eqnarray}G(x,\unicode[STIX]{x1D702},s)=1-\frac{\cosh \left[{\displaystyle \frac{\unicode[STIX]{x1D6FC}h_{o}}{2}}{\displaystyle \frac{1+\text{i}}{\sqrt{2}}}\left(2\unicode[STIX]{x1D702}-1\right)\right]}{\cosh \left[{\displaystyle \frac{\unicode[STIX]{x1D6FC}h_{o}}{2}}{\displaystyle \frac{1+\text{i}}{\sqrt{2}}}\right]}\end{eqnarray}$$
are determined by integration of
and
derived from (3.1) and (3.2), respectively. On the other hand, the function
![]() $G$
can be integrated to give
$G$
can be integrated to give
 $$\begin{eqnarray}\int _{0}^{\unicode[STIX]{x1D702}}G\,\text{d}\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}-\frac{1-\text{i}}{\sqrt{2}\unicode[STIX]{x1D6FC}h_{o}}\frac{\displaystyle \sinh \left[\frac{\unicode[STIX]{x1D6FC}h_{o}}{2}\frac{1+\text{i}}{\sqrt{2}}\left(2\unicode[STIX]{x1D702}-1\right)\right]+\sinh \left[\frac{\unicode[STIX]{x1D6FC}h_{o}}{2}\frac{1+\text{i}}{\sqrt{2}}\right]}{\displaystyle \cosh \left[\frac{\unicode[STIX]{x1D6FC}h_{o}}{2}\frac{1+\text{i}}{\sqrt{2}}\right]}\end{eqnarray}$$
$$\begin{eqnarray}\int _{0}^{\unicode[STIX]{x1D702}}G\,\text{d}\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}-\frac{1-\text{i}}{\sqrt{2}\unicode[STIX]{x1D6FC}h_{o}}\frac{\displaystyle \sinh \left[\frac{\unicode[STIX]{x1D6FC}h_{o}}{2}\frac{1+\text{i}}{\sqrt{2}}\left(2\unicode[STIX]{x1D702}-1\right)\right]+\sinh \left[\frac{\unicode[STIX]{x1D6FC}h_{o}}{2}\frac{1+\text{i}}{\sqrt{2}}\right]}{\displaystyle \cosh \left[\frac{\unicode[STIX]{x1D6FC}h_{o}}{2}\frac{1+\text{i}}{\sqrt{2}}\right]}\end{eqnarray}$$
which can be used in (3.5) to provide
 $$\begin{eqnarray}\displaystyle V & = & \displaystyle -\frac{1}{\ell }\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(\ell h_{o}\frac{\text{d}P^{\prime }}{\text{d}x}\int _{0}^{\unicode[STIX]{x1D702}}G\,\text{d}\unicode[STIX]{x1D702}\right)-\frac{1}{\ell }\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}s}\left(\frac{h_{o}}{\ell }\frac{\unicode[STIX]{x2202}\tilde{P}}{\unicode[STIX]{x2202}s}\int _{0}^{\unicode[STIX]{x1D702}}G\,\text{d}\unicode[STIX]{x1D702}\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x2202}h_{o}}{\unicode[STIX]{x2202}x}\frac{\text{d}P^{\prime }}{\text{d}x}\unicode[STIX]{x1D702}G+\frac{1}{\ell }\frac{\unicode[STIX]{x2202}h_{o}}{\unicode[STIX]{x2202}s}\frac{1}{\ell }\frac{\unicode[STIX]{x2202}\tilde{P}}{\unicode[STIX]{x2202}s}\unicode[STIX]{x1D702}G\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle V & = & \displaystyle -\frac{1}{\ell }\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(\ell h_{o}\frac{\text{d}P^{\prime }}{\text{d}x}\int _{0}^{\unicode[STIX]{x1D702}}G\,\text{d}\unicode[STIX]{x1D702}\right)-\frac{1}{\ell }\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}s}\left(\frac{h_{o}}{\ell }\frac{\unicode[STIX]{x2202}\tilde{P}}{\unicode[STIX]{x2202}s}\int _{0}^{\unicode[STIX]{x1D702}}G\,\text{d}\unicode[STIX]{x1D702}\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x2202}h_{o}}{\unicode[STIX]{x2202}x}\frac{\text{d}P^{\prime }}{\text{d}x}\unicode[STIX]{x1D702}G+\frac{1}{\ell }\frac{\unicode[STIX]{x2202}h_{o}}{\unicode[STIX]{x2202}s}\frac{1}{\ell }\frac{\unicode[STIX]{x2202}\tilde{P}}{\unicode[STIX]{x2202}s}\unicode[STIX]{x1D702}G\end{eqnarray}$$
for the velocity component normal to the surface.
The expressions given in (3.8) and (3.13) for the velocity components involve the pressure gradients
![]() $\text{d}P^{\prime }/\text{d}x$
and
$\text{d}P^{\prime }/\text{d}x$
and
![]() $\unicode[STIX]{x2202}\tilde{P}/\unicode[STIX]{x2202}s$
, to be obtained for given values of
$\unicode[STIX]{x2202}\tilde{P}/\unicode[STIX]{x2202}s$
, to be obtained for given values of
![]() $h_{o}(x,s)$
and
$h_{o}(x,s)$
and
![]() $\ell (x)$
with use made of (3.3) and (3.6). In the computation it is convenient to introduce the functions
$\ell (x)$
with use made of (3.3) and (3.6). In the computation it is convenient to introduce the functions
and
which define the volume fluxes
and
appearing in (3.3) and (3.6). In particular, equation (3.3) can be used, together with the boundary conditions (2.29) and (2.30), to write the boundary-value problem
for the function
![]() $P^{\prime }(x)$
, which can be used in (3.4) to give
$P^{\prime }(x)$
, which can be used in (3.4) to give
for the deformation of the outer surface and in (3.6) to yield
for the azimuthal pressure gradient.
In general, numerical integration is needed to solve the boundary-value problem (3.18). The closed-form solution
is obtained for uniform elastic modulus
![]() $E_{e}=1$
when the cross-section has constant shape (i.e.
$E_{e}=1$
when the cross-section has constant shape (i.e.
![]() $h_{o}=h_{o}(s)$
and
$h_{o}=h_{o}(s)$
and
![]() $\ell =A_{o}=1$
), so that
$\ell =A_{o}=1$
), so that
![]() $Q=\text{const}$
.
$Q=\text{const}$
.
For a given canal geometry, defined by
![]() $h_{o}(x,s)$
,
$h_{o}(x,s)$
,
![]() $\ell (x)$
and
$\ell (x)$
and
![]() $A_{o}(x)=\ell (x)\int _{0}^{1}h_{o}\,\text{d}s$
, with given elastic properties, defined by
$A_{o}(x)=\ell (x)\int _{0}^{1}h_{o}\,\text{d}s$
, with given elastic properties, defined by
![]() $E_{e}(x)$
, the determination of the oscillatory motion begins by employing (3.15) to compute
$E_{e}(x)$
, the determination of the oscillatory motion begins by employing (3.15) to compute
![]() $Q(x)$
. The resulting function is to be used in (3.18) when computing
$Q(x)$
. The resulting function is to be used in (3.18) when computing
![]() $P^{\prime }(x)$
, which in turn provides through (3.19) the deformation
$P^{\prime }(x)$
, which in turn provides through (3.19) the deformation
![]() $H^{\prime }$
. The associated gradient
$H^{\prime }$
. The associated gradient
![]() $\text{d}P^{\prime }/\text{d}x$
can be used in (3.8) to compute
$\text{d}P^{\prime }/\text{d}x$
can be used in (3.8) to compute
![]() $U$
and in (3.20) to evaluate
$U$
and in (3.20) to evaluate
![]() $\unicode[STIX]{x2202}\tilde{P}/\unicode[STIX]{x2202}s$
, which allows us to determine
$\unicode[STIX]{x2202}\tilde{P}/\unicode[STIX]{x2202}s$
, which allows us to determine
![]() $W$
and
$W$
and
![]() $V$
from (3.8) and (3.13). Finally, the complex functions
$V$
from (3.8) and (3.13). Finally, the complex functions
![]() $U$
,
$U$
,
![]() $V$
,
$V$
,
![]() $W$
,
$W$
,
![]() $P^{\prime }$
and
$P^{\prime }$
and
![]() $H^{\prime }$
can be used in (3.7) to provide
$H^{\prime }$
can be used in (3.7) to provide
![]() $u_{0}$
,
$u_{0}$
,
![]() $v_{0}$
,
$v_{0}$
,
![]() $w_{0}$
,
$w_{0}$
,
![]() $p_{0}^{\prime }$
and
$p_{0}^{\prime }$
and
![]() $h_{0}^{\prime }$
.
$h_{0}^{\prime }$
.
4 Steady-streaming motion
Because of nonlinear interactions, associated with the convective terms and with the temporal and spatial variations of the canal width, the first-order corrections to the flow contain a steady component, additional to the oscillatory component. The computation of this steady-streaming flow begins by collecting terms of order
![]() $\unicode[STIX]{x1D700}$
in (2.21) and (2.22). Taking the time average
$\unicode[STIX]{x1D700}$
in (2.21) and (2.22). Taking the time average
![]() $\langle \cdot \rangle =(1/2\unicode[STIX]{x03C0})\int _{0}^{2\unicode[STIX]{x03C0}}\cdot \,\,\text{d}t$
of the resulting equations yields
$\langle \cdot \rangle =(1/2\unicode[STIX]{x03C0})\int _{0}^{2\unicode[STIX]{x03C0}}\cdot \,\,\text{d}t$
of the resulting equations yields
where
 $$\begin{eqnarray}\displaystyle {\mathcal{F}}_{x} & = & \displaystyle \frac{1}{\ell }\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}(\ell \langle u_{0}^{2}\rangle )+\frac{1}{h_{o}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\langle u_{0}v_{0}\rangle +\frac{1}{\ell }\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}s}\langle u_{0}w_{0}\rangle \nonumber\\ \displaystyle & & \displaystyle -\,\frac{\unicode[STIX]{x1D702}}{h_{o}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left\langle \frac{\unicode[STIX]{x2202}h_{0}^{\prime }}{\unicode[STIX]{x2202}t}u_{0}\right\rangle -\frac{\unicode[STIX]{x2202}h_{o}}{\unicode[STIX]{x2202}x}\frac{\unicode[STIX]{x1D702}}{h_{o}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\langle u_{0}^{2}\rangle -\frac{1}{\ell }\frac{\unicode[STIX]{x2202}h_{o}}{\unicode[STIX]{x2202}s}\frac{\unicode[STIX]{x1D702}}{h_{o}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\langle u_{0}w_{0}\rangle +\frac{2}{h_{o}^{3}\unicode[STIX]{x1D6FC}^{2}}\frac{\unicode[STIX]{x2202}^{2}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}^{2}}\langle h_{0}^{\prime }u_{0}\rangle \qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{F}}_{x} & = & \displaystyle \frac{1}{\ell }\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}(\ell \langle u_{0}^{2}\rangle )+\frac{1}{h_{o}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\langle u_{0}v_{0}\rangle +\frac{1}{\ell }\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}s}\langle u_{0}w_{0}\rangle \nonumber\\ \displaystyle & & \displaystyle -\,\frac{\unicode[STIX]{x1D702}}{h_{o}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left\langle \frac{\unicode[STIX]{x2202}h_{0}^{\prime }}{\unicode[STIX]{x2202}t}u_{0}\right\rangle -\frac{\unicode[STIX]{x2202}h_{o}}{\unicode[STIX]{x2202}x}\frac{\unicode[STIX]{x1D702}}{h_{o}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\langle u_{0}^{2}\rangle -\frac{1}{\ell }\frac{\unicode[STIX]{x2202}h_{o}}{\unicode[STIX]{x2202}s}\frac{\unicode[STIX]{x1D702}}{h_{o}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\langle u_{0}w_{0}\rangle +\frac{2}{h_{o}^{3}\unicode[STIX]{x1D6FC}^{2}}\frac{\unicode[STIX]{x2202}^{2}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}^{2}}\langle h_{0}^{\prime }u_{0}\rangle \qquad\end{eqnarray}$$
and
 $$\begin{eqnarray}\displaystyle {\mathcal{F}}_{s} & = & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\langle u_{0}w_{0}\rangle +2\frac{\langle u_{0}w_{0}\rangle }{\ell }\frac{\unicode[STIX]{x2202}\ell }{\unicode[STIX]{x2202}x}+\frac{1}{h_{o}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\langle v_{0}w_{0}\rangle +\frac{1}{\ell }\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}s}\langle w_{0}^{2}\rangle -\frac{\unicode[STIX]{x1D702}}{h_{o}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left\langle \frac{\unicode[STIX]{x2202}h_{0}^{\prime }}{\unicode[STIX]{x2202}t}w_{0}\right\rangle \nonumber\\ \displaystyle & & \displaystyle -\,\frac{\unicode[STIX]{x2202}h_{o}}{\unicode[STIX]{x2202}x}\frac{\unicode[STIX]{x1D702}}{h_{o}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\langle u_{0}w_{0}\rangle -\frac{1}{\ell }\frac{\unicode[STIX]{x2202}h_{o}}{\unicode[STIX]{x2202}s}\frac{\unicode[STIX]{x1D702}}{h_{o}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\langle w_{0}^{2}\rangle +\frac{2}{h_{o}^{3}\unicode[STIX]{x1D6FC}^{2}}\frac{\unicode[STIX]{x2202}^{2}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}^{2}}\langle h_{0}^{\prime }w_{0}\rangle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{F}}_{s} & = & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\langle u_{0}w_{0}\rangle +2\frac{\langle u_{0}w_{0}\rangle }{\ell }\frac{\unicode[STIX]{x2202}\ell }{\unicode[STIX]{x2202}x}+\frac{1}{h_{o}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\langle v_{0}w_{0}\rangle +\frac{1}{\ell }\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}s}\langle w_{0}^{2}\rangle -\frac{\unicode[STIX]{x1D702}}{h_{o}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left\langle \frac{\unicode[STIX]{x2202}h_{0}^{\prime }}{\unicode[STIX]{x2202}t}w_{0}\right\rangle \nonumber\\ \displaystyle & & \displaystyle -\,\frac{\unicode[STIX]{x2202}h_{o}}{\unicode[STIX]{x2202}x}\frac{\unicode[STIX]{x1D702}}{h_{o}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\langle u_{0}w_{0}\rangle -\frac{1}{\ell }\frac{\unicode[STIX]{x2202}h_{o}}{\unicode[STIX]{x2202}s}\frac{\unicode[STIX]{x1D702}}{h_{o}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\langle w_{0}^{2}\rangle +\frac{2}{h_{o}^{3}\unicode[STIX]{x1D6FC}^{2}}\frac{\unicode[STIX]{x2202}^{2}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}^{2}}\langle h_{0}^{\prime }w_{0}\rangle\end{eqnarray}$$
can be evaluated in terms of the leading-order solution. The steady–streaming velocities must satisfy
![]() $\langle u_{1}\rangle =\langle w_{1}\rangle =0$
at
$\langle u_{1}\rangle =\langle w_{1}\rangle =0$
at
![]() $\unicode[STIX]{x1D702}=0,1$
.
$\unicode[STIX]{x1D702}=0,1$
.
The functions
![]() ${\mathcal{F}}_{x}$
and
${\mathcal{F}}_{x}$
and
![]() ${\mathcal{F}}_{s}$
drive the steady-streaming motion, in that, if they were zero, the solution to (4.1) and (4.2) would reduce to
${\mathcal{F}}_{s}$
drive the steady-streaming motion, in that, if they were zero, the solution to (4.1) and (4.2) would reduce to
![]() $\langle u_{1}\rangle =\langle w_{1}\rangle =0$
. Besides the well-known contributions arising from the time average of the nonlinear convective acceleration, present in any steady-streaming phenomenon, additional terms appear in (4.3) and (4.4) due to the deformation of the canal (i.e. the terms involving
$\langle u_{1}\rangle =\langle w_{1}\rangle =0$
. Besides the well-known contributions arising from the time average of the nonlinear convective acceleration, present in any steady-streaming phenomenon, additional terms appear in (4.3) and (4.4) due to the deformation of the canal (i.e. the terms involving
![]() $h_{0}^{\prime }$
and
$h_{0}^{\prime }$
and
![]() $\unicode[STIX]{x2202}h_{0}^{\prime }/\unicode[STIX]{x2202}t$
). Similar contributions have been identified earlier in studies of steady-streaming in elastic tubes (Wang & Tarbell Reference Wang and Tarbell1992). In principle, all terms in (4.3) and (4.4) can contribute significantly to the motion depending on the flow conditions and on the specific geometrical features of the canal. For the specific model problem considered below in § 5 the canal width
$\unicode[STIX]{x2202}h_{0}^{\prime }/\unicode[STIX]{x2202}t$
). Similar contributions have been identified earlier in studies of steady-streaming in elastic tubes (Wang & Tarbell Reference Wang and Tarbell1992). In principle, all terms in (4.3) and (4.4) can contribute significantly to the motion depending on the flow conditions and on the specific geometrical features of the canal. For the specific model problem considered below in § 5 the canal width
![]() $h_{o}$
and its perimeter
$h_{o}$
and its perimeter
![]() $\ell$
are selected to be independent of
$\ell$
are selected to be independent of
![]() $x$
, so that the terms involving
$x$
, so that the terms involving
![]() $\unicode[STIX]{x2202}h_{o}/\unicode[STIX]{x2202}x$
and
$\unicode[STIX]{x2202}h_{o}/\unicode[STIX]{x2202}x$
and
![]() $\unicode[STIX]{x2202}\ell /\unicode[STIX]{x2202}x$
are identically zero. All other terms were found to be significant, with their relative importance varying along the canal.
$\unicode[STIX]{x2202}\ell /\unicode[STIX]{x2202}x$
are identically zero. All other terms were found to be significant, with their relative importance varying along the canal.
Integrating (4.1) and (4.2) subject to
![]() $\langle u_{1}\rangle =\langle w_{1}\rangle =0$
at
$\langle u_{1}\rangle =\langle w_{1}\rangle =0$
at
![]() $\unicode[STIX]{x1D702}=0,1$
yields
$\unicode[STIX]{x1D702}=0,1$
yields
and
The average streamwise pressure gradient
![]() $\text{d}\langle p_{1}^{\prime }\rangle /\text{d}x$
, which completes the determination of
$\text{d}\langle p_{1}^{\prime }\rangle /\text{d}x$
, which completes the determination of
![]() $\langle u_{1}\rangle$
, is a function of
$\langle u_{1}\rangle$
, is a function of
![]() $x$
that can be computed by imposing the condition
$x$
that can be computed by imposing the condition
obtained at this order from the time average of (2.25) with use made of (2.30). Similarly, the azimuthal pressure gradient
![]() $\unicode[STIX]{x2202}\langle \tilde{p}_{1}\rangle /\unicode[STIX]{x2202}s$
appearing in (4.6) can be determined from the condition
$\unicode[STIX]{x2202}\langle \tilde{p}_{1}\rangle /\unicode[STIX]{x2202}s$
appearing in (4.6) can be determined from the condition
obtained at this order from the time average of (2.28).
5 Selected results for a model problem
A simple geometrical model will be used to illustrate some of the salient features of the flow. Specifically, we consider the flow in the annular canal bounded between two cylindrical surfaces of radii
![]() $R$
and
$R$
and
![]() $R+h_{c}$
whose axes are separated by a distance
$R+h_{c}$
whose axes are separated by a distance
![]() $\unicode[STIX]{x1D6FD}h_{c}$
, with
$\unicode[STIX]{x1D6FD}h_{c}$
, with
![]() $h_{c}\ll R$
and
$h_{c}\ll R$
and
![]() $0\leqslant \unicode[STIX]{x1D6FD}<1$
(see the schematic view shown in figure 4(a), to be discussed later). Using
$0\leqslant \unicode[STIX]{x1D6FD}<1$
(see the schematic view shown in figure 4(a), to be discussed later). Using
![]() $h_{c}$
and
$h_{c}$
and
![]() $\ell _{c}=2\unicode[STIX]{x03C0}R$
as characteristic scales leads to the dimensionless geometrical functions
$\ell _{c}=2\unicode[STIX]{x03C0}R$
as characteristic scales leads to the dimensionless geometrical functions
![]() $h_{o}=1-\unicode[STIX]{x1D6FD}\cos (2\unicode[STIX]{x03C0}s)$
,
$h_{o}=1-\unicode[STIX]{x1D6FD}\cos (2\unicode[STIX]{x03C0}s)$
,
![]() $\ell =1$
and
$\ell =1$
and
![]() $A_{o}=1$
, resulting in a constant value of the reduced volume flux
$A_{o}=1$
, resulting in a constant value of the reduced volume flux
![]() $Q$
, as can be computed from (3.15). Furthermore, a uniform elastic modulus
$Q$
, as can be computed from (3.15). Furthermore, a uniform elastic modulus
![]() $E_{e}=1$
is assumed, so that the complex function
$E_{e}=1$
is assumed, so that the complex function
![]() $P^{\prime }(x)$
for the axial pressure variation reduces to (3.21). Similar simple models involving coaxial flexible tubes have been considered in analyses of pressure-wave propagation in the spinal canal (Berkouk, Carpenter & Lucey Reference Berkouk, Carpenter and Lucey2003; Carpenter, Berkouk & Lucey Reference Carpenter, Berkouk and Lucey2003).
$P^{\prime }(x)$
for the axial pressure variation reduces to (3.21). Similar simple models involving coaxial flexible tubes have been considered in analyses of pressure-wave propagation in the spinal canal (Berkouk, Carpenter & Lucey Reference Berkouk, Carpenter and Lucey2003; Carpenter, Berkouk & Lucey Reference Carpenter, Berkouk and Lucey2003).
Besides the geometry, which is defined by the eccentricity parameter
![]() $\unicode[STIX]{x1D6FD}$
for the simplified problem, the solution depends on the values of
$\unicode[STIX]{x1D6FD}$
for the simplified problem, the solution depends on the values of
![]() $k$
and
$k$
and
![]() $\unicode[STIX]{x1D6FC}$
, both assumed to be of order unity, as corresponds to the scales characterizing the flow in the spinal canal. As can be seen from the definitions given in (2.10) and (2.20), the specific values
$\unicode[STIX]{x1D6FC}$
, both assumed to be of order unity, as corresponds to the scales characterizing the flow in the spinal canal. As can be seen from the definitions given in (2.10) and (2.20), the specific values
![]() $k=0.5$
and
$k=0.5$
and
![]() $\unicode[STIX]{x1D6FC}=3$
employed in the computations used for figures 3 through 5 correspond to a canal with width
$\unicode[STIX]{x1D6FC}=3$
employed in the computations used for figures 3 through 5 correspond to a canal with width
![]() $h_{c}\sim 1$
mm and elastic wave speed
$h_{c}\sim 1$
mm and elastic wave speed
![]() $(E_{c}/\unicode[STIX]{x1D70C})^{1/2}\sim 10~\text{m}~\text{s}^{-1}$
.
$(E_{c}/\unicode[STIX]{x1D70C})^{1/2}\sim 10~\text{m}~\text{s}^{-1}$
.
Figure 2. The value of
![]() $|Q\,\text{d}P^{\prime }/\text{d}x|$
evaluated with use made of (3.21) and (5.1) for
$|Q\,\text{d}P^{\prime }/\text{d}x|$
evaluated with use made of (3.21) and (5.1) for
![]() $h_{o}=1-\unicode[STIX]{x1D6FD}\cos (2\unicode[STIX]{x03C0}s)$
,
$h_{o}=1-\unicode[STIX]{x1D6FD}\cos (2\unicode[STIX]{x03C0}s)$
,
![]() $\ell =1$
and
$\ell =1$
and
![]() $\unicode[STIX]{x1D6FD}=0.5$
. Panel (a) shows the variation with
$\unicode[STIX]{x1D6FD}=0.5$
. Panel (a) shows the variation with
![]() $x$
, whereas (b) shows the parametric dependence of the entrance value
$x$
, whereas (b) shows the parametric dependence of the entrance value
![]() $|Q\,\text{d}P^{\prime }/\text{d}x|_{x=0}$
.
$|Q\,\text{d}P^{\prime }/\text{d}x|_{x=0}$
.
The leading-order oscillatory flow is investigated in figures 2 and 3. In particular, figure 2 represents the variation of
which is the amplitude of the tidal volume flux across the canal, according to (3.17). The plot includes the variation of this quantity with
![]() $x$
as well as the dependences of the entrance value
$x$
as well as the dependences of the entrance value
![]() $|Q\,\text{d}P^{\prime }/\text{d}x|_{x=0}=|(\sqrt{Q}/k)\tan (k/\sqrt{Q})|$
on
$|Q\,\text{d}P^{\prime }/\text{d}x|_{x=0}=|(\sqrt{Q}/k)\tan (k/\sqrt{Q})|$
on
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $k$
for
$k$
for
![]() $\unicode[STIX]{x1D6FD}=0.5$
. Additional computations for other values of
$\unicode[STIX]{x1D6FD}=0.5$
. Additional computations for other values of
![]() $\unicode[STIX]{x1D6FD}$
(not shown here) revealed that the eccentricity has a negligible effect on the tidal volume flux, so that the curves obtained with
$\unicode[STIX]{x1D6FD}$
(not shown here) revealed that the eccentricity has a negligible effect on the tidal volume flux, so that the curves obtained with
![]() $\unicode[STIX]{x1D6FD}\neq 0.5$
are almost identical to those plotted in the figure.
$\unicode[STIX]{x1D6FD}\neq 0.5$
are almost identical to those plotted in the figure.

Figure 3. The distribution of
![]() $|u_{0}|=|U|$
for
$|u_{0}|=|U|$
for
![]() $k=0.5$
and
$k=0.5$
and
![]() $\unicode[STIX]{x1D6FC}=3$
as obtained at different sections
$\unicode[STIX]{x1D6FC}=3$
as obtained at different sections
![]() $x$
for varying eccentricities.
$x$
for varying eccentricities.
As can be seen in figure 2(a), the tidal volume flux decreases along the canal to vanish at the closed end. As expected, larger values of
![]() $\unicode[STIX]{x1D6FC}$
, associated with smaller viscous forces, result in increased flow rates. The dependence of
$\unicode[STIX]{x1D6FC}$
, associated with smaller viscous forces, result in increased flow rates. The dependence of
![]() $|Q\,\text{d}P^{\prime }/\text{d}x|_{x=0}$
on
$|Q\,\text{d}P^{\prime }/\text{d}x|_{x=0}$
on
![]() $k$
is shown in figure 2(b). For small
$k$
is shown in figure 2(b). For small
![]() $k$
, i.e. wavelengths that are much larger than the canal length, the pressure along the canal is almost uniform, and the dura membrane deforms uniformly in response to the pressure oscillations in the cranial cavity, following (2.26), resulting in an entrance flow rate that is independent of the flow conditions, so that the value of
$k$
, i.e. wavelengths that are much larger than the canal length, the pressure along the canal is almost uniform, and the dura membrane deforms uniformly in response to the pressure oscillations in the cranial cavity, following (2.26), resulting in an entrance flow rate that is independent of the flow conditions, so that the value of
![]() $|Q\,\text{d}P^{\prime }/\text{d}x|_{x=0}$
for
$|Q\,\text{d}P^{\prime }/\text{d}x|_{x=0}$
for
![]() $k\ll 1$
is identical for all
$k\ll 1$
is identical for all
![]() $\unicode[STIX]{x1D6FC}$
. In the opposite limit
$\unicode[STIX]{x1D6FC}$
. In the opposite limit
![]() $k\gg 1$
the wavelength is much shorter than the canal length, so that at a given instant of time we find regions of positive and negative deformation of the dura membrane along the canal, which tend to have a cancelling effect on the entrance flow rate, reflected in the decrease of
$k\gg 1$
the wavelength is much shorter than the canal length, so that at a given instant of time we find regions of positive and negative deformation of the dura membrane along the canal, which tend to have a cancelling effect on the entrance flow rate, reflected in the decrease of
![]() $|Q\,\text{d}P^{\prime }/\text{d}x|_{x=0}$
for
$|Q\,\text{d}P^{\prime }/\text{d}x|_{x=0}$
for
![]() $k\gg 1$
. An interesting result from the model is that
$k\gg 1$
. An interesting result from the model is that
![]() $|Q\,\text{d}P^{\prime }/\text{d}x|_{x=0}$
reaches a maximum at an intermediate value of the wavenumber
$|Q\,\text{d}P^{\prime }/\text{d}x|_{x=0}$
reaches a maximum at an intermediate value of the wavenumber
![]() $k$
(i.e.
$k$
(i.e.
![]() $k\simeq 1$
for
$k\simeq 1$
for
![]() $\unicode[STIX]{x1D6FC}=3$
), associated with elastic wave speeds
$\unicode[STIX]{x1D6FC}=3$
), associated with elastic wave speeds
![]() $(E_{c}/\unicode[STIX]{x1D70C})^{1/2}$
on the order of
$(E_{c}/\unicode[STIX]{x1D70C})^{1/2}$
on the order of
![]() $\unicode[STIX]{x1D714}L$
.
$\unicode[STIX]{x1D714}L$
.
Although variations of the eccentricity do not significantly alter the tidal volume flux, the velocity fields associated with different values of
![]() $\unicode[STIX]{x1D6FD}$
are very different, as seen in the comparisons in figure 3, which exhibit the distributions of streamwise velocity amplitude
$\unicode[STIX]{x1D6FD}$
are very different, as seen in the comparisons in figure 3, which exhibit the distributions of streamwise velocity amplitude
![]() $|u_{0}|=|U|$
at different cross-sections and for varying eccentricities, including the concentric case,
$|u_{0}|=|U|$
at different cross-sections and for varying eccentricities, including the concentric case,
![]() $\unicode[STIX]{x1D6FD}=0$
. Although the analytical solution given above applies only to configurations with
$\unicode[STIX]{x1D6FD}=0$
. Although the analytical solution given above applies only to configurations with
![]() $h_{c}\ll R$
, the width of the annular cross-section in the figure is arbitrarily enlarged to facilitate visualization. As expected, the decelerating effect of viscous forces becomes more (less) effective in regions of smaller (larger) canal width, leading to the nonuniform velocity distributions depicted in the figure.
$h_{c}\ll R$
, the width of the annular cross-section in the figure is arbitrarily enlarged to facilitate visualization. As expected, the decelerating effect of viscous forces becomes more (less) effective in regions of smaller (larger) canal width, leading to the nonuniform velocity distributions depicted in the figure.

Figure 4. Schematic view of the model geometry considered here (a), distribution of
![]() $\langle u_{1}\rangle$
corresponding to
$\langle u_{1}\rangle$
corresponding to
![]() $k=0.5$
,
$k=0.5$
,
![]() $\unicode[STIX]{x1D6FC}=3$
and
$\unicode[STIX]{x1D6FC}=3$
and
![]() $\unicode[STIX]{x1D6FD}=0.5$
(b), and streamwise variation of the maximum (downward) and minimum (upward) velocities for different values of
$\unicode[STIX]{x1D6FD}=0.5$
(b), and streamwise variation of the maximum (downward) and minimum (upward) velocities for different values of
![]() $\unicode[STIX]{x1D6FD}$
(c).
$\unicode[STIX]{x1D6FD}$
(c).
Steady streaming velocities
![]() $\langle u_{1}\rangle$
, evaluated for
$\langle u_{1}\rangle$
, evaluated for
![]() $k=0.5$
and
$k=0.5$
and
![]() $\unicode[STIX]{x1D6FC}=3$
from (4.5) with
$\unicode[STIX]{x1D6FC}=3$
from (4.5) with
![]() $\text{d}\langle p_{1}^{\prime }\rangle /\text{d}x$
computed using (4.7), are plotted in figures 4 and 5. The circular plot in figure 4(b) shows the distribution of
$\text{d}\langle p_{1}^{\prime }\rangle /\text{d}x$
computed using (4.7), are plotted in figures 4 and 5. The circular plot in figure 4(b) shows the distribution of
![]() $\langle u_{1}\rangle$
for
$\langle u_{1}\rangle$
for
![]() $\unicode[STIX]{x1D6FD}=0.5$
and
$\unicode[STIX]{x1D6FD}=0.5$
and
![]() $x=0.25$
. Transverse profiles of
$x=0.25$
. Transverse profiles of
![]() $\langle u_{1}\rangle$
across the narrowest (
$\langle u_{1}\rangle$
across the narrowest (
![]() $s=0$
) and widest (
$s=0$
) and widest (
![]() $s=1/2$
) sections are plotted below at different heights for this same eccentricity. As can be seen, the resulting velocities are negative (upwards) in the narrow part of the canal and predominantly positive (downwards) in the wider regions. The associated flow pattern is schematically represented by the arrows in figure 4(a).
$s=1/2$
) sections are plotted below at different heights for this same eccentricity. As can be seen, the resulting velocities are negative (upwards) in the narrow part of the canal and predominantly positive (downwards) in the wider regions. The associated flow pattern is schematically represented by the arrows in figure 4(a).
The circular plots in figure 5 represent distributions of
![]() $\langle u_{1}\rangle$
across the canal section at different heights and eccentricities, as in figure 3. The computations for
$\langle u_{1}\rangle$
across the canal section at different heights and eccentricities, as in figure 3. The computations for
![]() $\unicode[STIX]{x1D6FD}\neq 0$
reveal that the maximum velocity
$\unicode[STIX]{x1D6FD}\neq 0$
reveal that the maximum velocity
![]() $\langle u_{1}\rangle _{max}$
always occurs in the symmetry plane at the centre point of the widest section. By way of contrast, negative (upward) velocities are found in the narrow part of the canal, in agreement with the transverse profiles shown in figure 4. The minimum velocity
$\langle u_{1}\rangle _{max}$
always occurs in the symmetry plane at the centre point of the widest section. By way of contrast, negative (upward) velocities are found in the narrow part of the canal, in agreement with the transverse profiles shown in figure 4. The minimum velocity
![]() $\langle u_{1}\rangle _{min}$
occurs at the narrowest section
$\langle u_{1}\rangle _{min}$
occurs at the narrowest section
![]() $s=0$
for sufficiently small values of
$s=0$
for sufficiently small values of
![]() $\unicode[STIX]{x1D6FD}>0$
but moves away from the symmetry plane for large eccentricities, as can be clearly observed in the results for
$\unicode[STIX]{x1D6FD}>0$
but moves away from the symmetry plane for large eccentricities, as can be clearly observed in the results for
![]() $\unicode[STIX]{x1D6FD}=0.75$
. Also of interest is the fact that, as can be inferred from the plots corresponding to
$\unicode[STIX]{x1D6FD}=0.75$
. Also of interest is the fact that, as can be inferred from the plots corresponding to
![]() $\unicode[STIX]{x1D6FD}=0$
, the apparent volume flux
$\unicode[STIX]{x1D6FD}=0$
, the apparent volume flux
![]() $\int _{0}^{1}h_{o}(\int _{0}^{1}\langle u_{1}\rangle \,\text{d}\unicode[STIX]{x1D702})\,\text{d}s$
associated with the steady-steaming flow is nonzero, that being a direct consequence of the deformation of the canal wall, which enters in the integral continuity balance (4.7).
$\int _{0}^{1}h_{o}(\int _{0}^{1}\langle u_{1}\rangle \,\text{d}\unicode[STIX]{x1D702})\,\text{d}s$
associated with the steady-steaming flow is nonzero, that being a direct consequence of the deformation of the canal wall, which enters in the integral continuity balance (4.7).
The distributions of
![]() $\langle u_{1}\rangle _{max}$
and
$\langle u_{1}\rangle _{max}$
and
![]() $\langle u_{1}\rangle _{min}$
along the canal are plotted on figure 4(b) for different values of
$\langle u_{1}\rangle _{min}$
along the canal are plotted on figure 4(b) for different values of
![]() $\unicode[STIX]{x1D6FD}$
. The bulk motion, characterized by these two bounding values, is found to be extremely weak for concentric cylinders, but becomes much more pronounced for eccentric canals, for which we find values of
$\unicode[STIX]{x1D6FD}$
. The bulk motion, characterized by these two bounding values, is found to be extremely weak for concentric cylinders, but becomes much more pronounced for eccentric canals, for which we find values of
![]() $\langle u_{1}\rangle$
of order unity, corresponding to dimensional steady-streaming velocities of order
$\langle u_{1}\rangle$
of order unity, corresponding to dimensional steady-streaming velocities of order
![]() $\unicode[STIX]{x1D700}^{2}\unicode[STIX]{x1D714}L$
. It is also of interest that the configuration with intermediate eccentricity (
$\unicode[STIX]{x1D700}^{2}\unicode[STIX]{x1D714}L$
. It is also of interest that the configuration with intermediate eccentricity (
![]() $\unicode[STIX]{x1D6FD}=0.5$
) exhibits velocities that are larger than those found with
$\unicode[STIX]{x1D6FD}=0.5$
) exhibits velocities that are larger than those found with
![]() $\unicode[STIX]{x1D6FD}=0.25$
and
$\unicode[STIX]{x1D6FD}=0.25$
and
![]() $\unicode[STIX]{x1D6FD}=0.75$
. This non-monotonic dependence, associated with the nonlinear interactions of the steady-streaming flow, is an indication of the importance of the geometrical effects. The results suggest that accurate quantifications of CSF flow in the spinal canal should consider the specific geometric features of the SAS, described in our model by the functions
$\unicode[STIX]{x1D6FD}=0.75$
. This non-monotonic dependence, associated with the nonlinear interactions of the steady-streaming flow, is an indication of the importance of the geometrical effects. The results suggest that accurate quantifications of CSF flow in the spinal canal should consider the specific geometric features of the SAS, described in our model by the functions
![]() $h_{o}(x,s)$
and
$h_{o}(x,s)$
and
![]() $\ell (x)$
.
$\ell (x)$
.

Figure 5. The distribution of
![]() $\langle u_{1}\rangle$
for
$\langle u_{1}\rangle$
for
![]() $k=0.5$
and
$k=0.5$
and
![]() $\unicode[STIX]{x1D6FC}=3$
as obtained at different sections
$\unicode[STIX]{x1D6FC}=3$
as obtained at different sections
![]() $x$
for varying eccentricities.
$x$
for varying eccentricities.
For completeness, the distributions of azimuthal velocity
![]() $\langle w_{1}\rangle$
across the canal section are shown in figure 6 for the case
$\langle w_{1}\rangle$
across the canal section are shown in figure 6 for the case
![]() $k=0.5$
and
$k=0.5$
and
![]() $\unicode[STIX]{x1D6FC}=3$
corresponding to the plots in figure 5. As can be seen, the distributions exhibit the expected symmetry, with the azimuthal velocity vanishing at the symmetry plane, defined by the sections
$\unicode[STIX]{x1D6FC}=3$
corresponding to the plots in figure 5. As can be seen, the distributions exhibit the expected symmetry, with the azimuthal velocity vanishing at the symmetry plane, defined by the sections
![]() $s=0$
and
$s=0$
and
![]() $s=0.5$
. The circumferential motion, identically zero for concentric configurations, becomes more pronounced for increasing
$s=0.5$
. The circumferential motion, identically zero for concentric configurations, becomes more pronounced for increasing
![]() $\unicode[STIX]{x1D6FD}$
, with the configuration with
$\unicode[STIX]{x1D6FD}$
, with the configuration with
![]() $\unicode[STIX]{x1D6FD}=0.5$
exhibiting the largest values of
$\unicode[STIX]{x1D6FD}=0.5$
exhibiting the largest values of
![]() $\langle w_{1}\rangle$
. It is also of interest that the azimuthal motion is faster near the canal end, as needed to accommodate the more rapid deceleration of the streamwise motion occurring there, which is apparent in figure 4(c). The location of the peak values of
$\langle w_{1}\rangle$
. It is also of interest that the azimuthal motion is faster near the canal end, as needed to accommodate the more rapid deceleration of the streamwise motion occurring there, which is apparent in figure 4(c). The location of the peak values of
![]() $\langle w_{1}\rangle$
, found near
$\langle w_{1}\rangle$
, found near
![]() $s\approx 0.25$
at the entrance, progressively move towards the narrowest section (
$s\approx 0.25$
at the entrance, progressively move towards the narrowest section (
![]() $s=0$
) for increasing values of
$s=0$
) for increasing values of
![]() $x$
, an effect that is more noticeable as
$x$
, an effect that is more noticeable as
![]() $\unicode[STIX]{x1D6FD}$
increases.
$\unicode[STIX]{x1D6FD}$
increases.
Figure 6. The distribution of
![]() $\langle w_{1}\rangle$
for
$\langle w_{1}\rangle$
for
![]() $k=0.5$
and
$k=0.5$
and
![]() $\unicode[STIX]{x1D6FC}=3$
as obtained at different sections
$\unicode[STIX]{x1D6FC}=3$
as obtained at different sections
![]() $x$
for varying eccentricities.
$x$
for varying eccentricities.
6 Experiments of steady streaming in slender elastic annular tubes
We have conducted a series of in-vitro experiments in order to qualitatively validate the predictions of our asymptotic analysis. The experiments involve the simplified geometry depicted in figure 4(a), that is, a straight, slender, elastic annular canal of length
![]() $L=25~\text{cm}$
bounded between cylindrical tubes of radii
$L=25~\text{cm}$
bounded between cylindrical tubes of radii
![]() $R=7~\text{mm}$
and
$R=7~\text{mm}$
and
![]() $R+h_{c}=10.5~\text{mm}$
. Axisymmetric cases (
$R+h_{c}=10.5~\text{mm}$
. Axisymmetric cases (
![]() $\unicode[STIX]{x1D6FD}=0$
) with coaxial tubes were investigated along with a case with eccentricity
$\unicode[STIX]{x1D6FD}=0$
) with coaxial tubes were investigated along with a case with eccentricity
![]() $\unicode[STIX]{x1D6FD}=0.1$
. The annular tube is connected at one end to a rigid container where the pressure
$\unicode[STIX]{x1D6FD}=0.1$
. The annular tube is connected at one end to a rigid container where the pressure
![]() $p_{c}$
is varied periodically through a peristaltic pump with a frequency of 1 Hz to produce an oscillatory flow at the entrance of the channel of
$p_{c}$
is varied periodically through a peristaltic pump with a frequency of 1 Hz to produce an oscillatory flow at the entrance of the channel of
![]() $\pm 2~\text{cm}~\text{s}^{-1}$
. The values of
$\pm 2~\text{cm}~\text{s}^{-1}$
. The values of
![]() $h_{c}$
and
$h_{c}$
and
![]() $\unicode[STIX]{x1D714}$
yield
$\unicode[STIX]{x1D714}$
yield
![]() $\unicode[STIX]{x1D6FC}=h_{c}/(\unicode[STIX]{x1D708}/\unicode[STIX]{x1D714})^{1/2}\simeq 8.7$
for the associated Womersley number. The ratio of the displaced volume to that contained in the unperturbed annular tube was selected to be
$\unicode[STIX]{x1D6FC}=h_{c}/(\unicode[STIX]{x1D708}/\unicode[STIX]{x1D714})^{1/2}\simeq 8.7$
for the associated Womersley number. The ratio of the displaced volume to that contained in the unperturbed annular tube was selected to be
![]() $\unicode[STIX]{x0394}V/V=1/50$
, consistent with the values in the clinical observations. The results shown below correspond to an elastic outer tube, representing the deformable dura membrane, with an inner rigid rod, representing the spinal cord. Additional experiments using an inner elastic tube surrounded by a rigid outer cylinder and two elastic tubes were found to give similar flow features.
$\unicode[STIX]{x0394}V/V=1/50$
, consistent with the values in the clinical observations. The results shown below correspond to an elastic outer tube, representing the deformable dura membrane, with an inner rigid rod, representing the spinal cord. Additional experiments using an inner elastic tube surrounded by a rigid outer cylinder and two elastic tubes were found to give similar flow features.
The flow velocity was measured in a coaxial plane at various downstream locations along the tube by particle image velocimetry (PIV) using neutrally buoyant hollow, spherical, silver-coated micro particles with a diameter of
![]() $0.5~\unicode[STIX]{x03BC}\text{m}$
. Figure 7 shows the time variation of the oscillatory velocity, averaged over the cross-section of the annular gap at various downstream locations along the tube for the case of a concentric annular tube (
$0.5~\unicode[STIX]{x03BC}\text{m}$
. Figure 7 shows the time variation of the oscillatory velocity, averaged over the cross-section of the annular gap at various downstream locations along the tube for the case of a concentric annular tube (
![]() $\unicode[STIX]{x1D6FD}=0$
). The flow corresponds to a pure harmonic motion of biphasic periodic tides of ebb-and-flow with frequency
$\unicode[STIX]{x1D6FD}=0$
). The flow corresponds to a pure harmonic motion of biphasic periodic tides of ebb-and-flow with frequency
![]() $\unicode[STIX]{x1D714}$
, with amplitudes monotonically decreasing as one moves from the open end to the closed end of the annular tube, consistent with the predictions of the zeroth-order solution of the asymptotic analysis shown in figures 2 and 3, and as also observed in many clinical MRI measurements.
$\unicode[STIX]{x1D714}$
, with amplitudes monotonically decreasing as one moves from the open end to the closed end of the annular tube, consistent with the predictions of the zeroth-order solution of the asymptotic analysis shown in figures 2 and 3, and as also observed in many clinical MRI measurements.
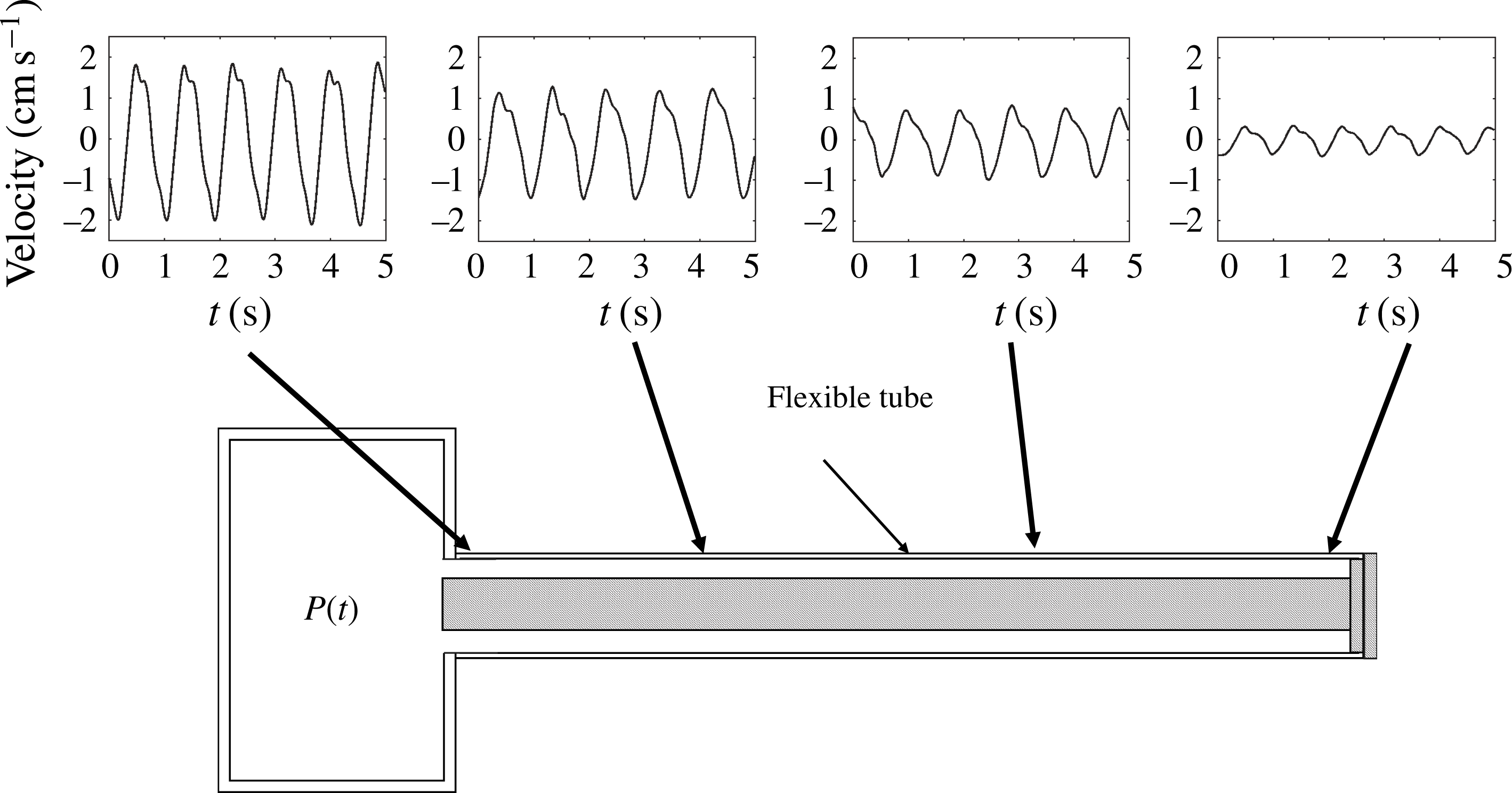
Figure 7. Time variation of the oscillatory axial velocity averaged along the cross-section at various downstream locations along the tube for the case of an axisymmetric annular canal (
![]() $\unicode[STIX]{x1D6FD}=0$
) with flexible outer wall and rigid inner surface.
$\unicode[STIX]{x1D6FD}=0$
) with flexible outer wall and rigid inner surface.

Figure 8. (a) Time evolution of the fluorescent marker initially injected in the annular gap at the midpoint between the entrance and closed end of the tube. The open entrance to the channel is located on the left-hand side. (b) Schematic representation of the evolution of the fluorescent marker injected at the midpoint along the tube. (c) Propagation velocity of the dye front towards the open entrance of the tube. Note the monotonic increase of the streaming velocity
![]() $\langle u_{1}\rangle$
approaching the open entrance. The measurements correspond to an eccentric case with
$\langle u_{1}\rangle$
approaching the open entrance. The measurements correspond to an eccentric case with
![]() $\unicode[STIX]{x1D6FD}=0.1$
$\unicode[STIX]{x1D6FD}=0.1$
The PIV measurements were sufficiently accurate to capture the decay in the amplitude of the leading-order oscillatory flow as shown in figure 7. Unfortunately, the polymer tubes that are necessary for simulation of the compliance of the canal are not optically clean and give rise to undesirable reflections and scattering effects that affected the accuracy of the PIV velocity measurements near the walls of the narrow annular gap. Because the resulting measurement error is much greater than the streaming velocities, integrating these measurements over 20–30 min (1200–1800 cycles) results in very noisy measurements. Thus, to quantify the velocity of the streaming motion we opted to use the far more reliable method of injecting a bolus of neutrally buoyant fluorescent dye in the annular gap of the canal at the midpoint between its entrance and closed end, and accurately measure over 20–30 min the velocity of the upward and downward propagation of the fronts as shown in the schematic panels of figure 8. We selected this method not only for its accuracy compared to the PIV measurements but also because it fully resembles the technique used in all the radiological measurements done in the clinical setting, where a bolus of marker is injected in the lumbar region, making our results easier to understand by the medical community. The tube was oriented horizontally with the inner tube offset slightly to introduce an eccentricity (
![]() $\unicode[STIX]{x1D6FD}=0.1$
), as shown in figure 8(b).
$\unicode[STIX]{x1D6FD}=0.1$
), as shown in figure 8(b).
The annular tube was illuminated with an ultraviolet light and imaged using a CCD camera with a resolution of
![]() $2000\times 2000~\text{pixels}$
. Fluorescence images were recorded at the same oscillation phase every 30 s over 20 min to track the time evolution of the injected patch. Figure 8 shows the images at 150 s intervals for the first 15 min. These measurements clearly demonstrate that, in addition to the periodic harmonic oscillatory motion described in figure 7, there is a bulk motion that gradually transports the dye upwards (to the left in this experiment) into the tank and downwards (right) towards the closed end. Measurements of the speed at which these two fronts propagate allowed us to obtain order-of-magnitude estimates for the local velocity of the mean streaming motion (as an example, figure 8(c) represents the upward velocity of the front recorded in one of the experiments). Consistent with the analysis in § 5, we found that the speed of the dye front propagating towards the tank gradually increases as the open end is approached, while at the same time the speed of the opposite front moving to the right decreases on approaching the closed end of the tube, in agreement with the results in figures 4 and 5. It is important to emphasize that, as predicted by the analysis, these streaming velocities are a factor
$2000\times 2000~\text{pixels}$
. Fluorescence images were recorded at the same oscillation phase every 30 s over 20 min to track the time evolution of the injected patch. Figure 8 shows the images at 150 s intervals for the first 15 min. These measurements clearly demonstrate that, in addition to the periodic harmonic oscillatory motion described in figure 7, there is a bulk motion that gradually transports the dye upwards (to the left in this experiment) into the tank and downwards (right) towards the closed end. Measurements of the speed at which these two fronts propagate allowed us to obtain order-of-magnitude estimates for the local velocity of the mean streaming motion (as an example, figure 8(c) represents the upward velocity of the front recorded in one of the experiments). Consistent with the analysis in § 5, we found that the speed of the dye front propagating towards the tank gradually increases as the open end is approached, while at the same time the speed of the opposite front moving to the right decreases on approaching the closed end of the tube, in agreement with the results in figures 4 and 5. It is important to emphasize that, as predicted by the analysis, these streaming velocities are a factor
![]() $\unicode[STIX]{x1D700}$
smaller (i.e. about two orders of magnitude) than the amplitude of the velocity fluctuations measured for the harmonic base flow described above. Our results are consistent with many radiological measurements; see, for example, the measurements of Greitz & Hannerz (Reference Greitz and Hannerz1996), who showed in their radionuclide cisternography (figure 4 in that paper) that tracers injected in the lumbar region reached the thoracic area much faster than they moved downwards into the sacral end.
$\unicode[STIX]{x1D700}$
smaller (i.e. about two orders of magnitude) than the amplitude of the velocity fluctuations measured for the harmonic base flow described above. Our results are consistent with many radiological measurements; see, for example, the measurements of Greitz & Hannerz (Reference Greitz and Hannerz1996), who showed in their radionuclide cisternography (figure 4 in that paper) that tracers injected in the lumbar region reached the thoracic area much faster than they moved downwards into the sacral end.
We have further corroborated that the observed bulk transport is not due to any gravitational or thermal effects by repeating the above experiments without the imposed pressure pulsations in the tank. For this case, the dye diffused only several millimetres left and right over 10 h.
7 Conclusions
We have investigated the physical mechanism responsible for recirculation of CSF in the spinal canal by formulating an asymptotic analysis of a physiologically relevant geometry accounting for the small compliance of the dura membrane through a small parameter
![]() $\unicode[STIX]{x1D700}$
, on the order of the ratio of the tidal volume to the total CSF volume in the spinal canal. We have shown that the flow at leading order, in the limit
$\unicode[STIX]{x1D700}$
, on the order of the ratio of the tidal volume to the total CSF volume in the spinal canal. We have shown that the flow at leading order, in the limit
![]() $\unicode[STIX]{x1D700}\ll 1$
, reduces to an oscillatory linear lubrication problem, while the first-order corrections provide the description for the steady-streaming flow, responsible for the bulk motion along the canal.
$\unicode[STIX]{x1D700}\ll 1$
, reduces to an oscillatory linear lubrication problem, while the first-order corrections provide the description for the steady-streaming flow, responsible for the bulk motion along the canal.
The general asymptotic formulation has been applied to the simplified case of a closed-end, compliant, constant diameter tube (spinal canal) containing an eccentric coaxial cylindrical insert (spinal cord). We have shown that, consistent with radiological observations in human adults, the small pressure pulsation imposed at the entrance results in an oscillatory motion whose amplitude decreases along the length of the compliant canal. We have also demonstrated that this oscillatory motion induces a slow streaming motion with velocities two orders of magnitude smaller, and establishes a slow recirculating bulk motion bringing fluid downwards along the canal and returning it upwards to its entrance. The amplitude of the oscillatory flow measured by MRI in human subjects in the cervical region is
![]() $1{-}2~\text{cm}~\text{s}^{-1}$
decreasing as one moves downwards along the spinal canal, and one can then estimate from our analysis the magnitude of the mean steady streaming velocity (bulk recirculating flow) of the CSF in the human spinal canal in physiologically relevant conditions to be on the order of
$1{-}2~\text{cm}~\text{s}^{-1}$
decreasing as one moves downwards along the spinal canal, and one can then estimate from our analysis the magnitude of the mean steady streaming velocity (bulk recirculating flow) of the CSF in the human spinal canal in physiologically relevant conditions to be on the order of
![]() $1{-}2~\text{cm}~\text{min}^{-1}$
, which is also consistent with radiological observations. Based on the values of the variation of the streaming velocity experimentally measured along the length of the canal, one can estimate the time for the bulk recirculating flow to refresh the whole CSF in and out of the canal to be on the order of a few hours.
$1{-}2~\text{cm}~\text{min}^{-1}$
, which is also consistent with radiological observations. Based on the values of the variation of the streaming velocity experimentally measured along the length of the canal, one can estimate the time for the bulk recirculating flow to refresh the whole CSF in and out of the canal to be on the order of a few hours.
In summary, our analysis of an idealized geometry of the spinal canal has provided a mechanistic physical explanation of a known physiological process that has remained unexplained for the past 50 years. Although the anatomy of the SAS in the spinal canal is far more complex than the specific geometry used in the exploratory quantification presented above, the order of magnitude of the results is fully consistent with current radiological observations. The formulation developed here, combined with and accurate anatomical descriptions of the SAS geometry, given by the functions
![]() $h_{o}(x,s)$
and
$h_{o}(x,s)$
and
![]() $\ell (x)$
, and of the elastic properties of the dura membrane, embodied in the distribution of
$\ell (x)$
, and of the elastic properties of the dura membrane, embodied in the distribution of
![]() $E_{e}(x)$
, could be employed in future work to develop more accurate quantitative predictions. Our formulation could also be extended to account for additional effects, including a more detailed description of the elastic properties of the dura membrane as well as the possible axial oscillatory motion of the spinal cord. The contribution to the Lagrangian motion arising from Stokes drift could be evaluated on the basis of the leading-order velocity description. Also, corrections associated with shear-enhanced diffusion, anticipated to be small in our previous estimates, could be incorporated in the model by introducing a passive scalar governed by an unsteady convection–diffusion equation. The improved understanding of the mechanism regulating the bulk motion of the CSF in the spinal canal resulting from this analysis may have potential implications in optimizing intrathecal targeted drug delivery systems (injecting the drug directly in the CSF around the spinal cord) and in improving the current understanding of the etiology of a large class of neurological conditions.
$E_{e}(x)$
, could be employed in future work to develop more accurate quantitative predictions. Our formulation could also be extended to account for additional effects, including a more detailed description of the elastic properties of the dura membrane as well as the possible axial oscillatory motion of the spinal cord. The contribution to the Lagrangian motion arising from Stokes drift could be evaluated on the basis of the leading-order velocity description. Also, corrections associated with shear-enhanced diffusion, anticipated to be small in our previous estimates, could be incorporated in the model by introducing a passive scalar governed by an unsteady convection–diffusion equation. The improved understanding of the mechanism regulating the bulk motion of the CSF in the spinal canal resulting from this analysis may have potential implications in optimizing intrathecal targeted drug delivery systems (injecting the drug directly in the CSF around the spinal cord) and in improving the current understanding of the etiology of a large class of neurological conditions.
Acknowledgements
C.M.-B. wants to thank the Spanish MEDC and the Salvador Madariaga Program for the financial support provided during their sabbatical stay at UC San Diego. E.C.-H. would like to thank ‘la Caixa’ (Caja de Ahorros y Pensiones de Barcelona) for partial financial support through a ‘la Caixa’ Fellowship. We wish to dedicate this work to Professor W. (Bill) Bradley who suddenly passed away on November 20th, 2017, just days before this manuscript was accepted for publication. Bill was an outstanding neuroradiologist and the source of the inspiration that guided our work on the motion of the CSF in the CNS.