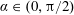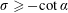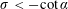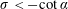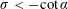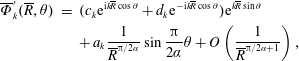1 Introduction
In Gallagher, Needham & Billingham (Reference Gallagher, Needham and Billingham2018) (henceforth referred to as GNB) we considered the problem of the two-dimensional, irrotational flow generated by the uniform acceleration of a flat, rigid plate, inclined at an angle
![]() $\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
to the horizontal, into or away from a uniform, horizontal strip of inviscid fluid under gravity. This work followed on from that of King & Needham (Reference King and Needham1994), Needham, Billingham & King (Reference Needham, Billingham and King2007), Needham, Chamberlain & Billingham (Reference Needham, Chamberlain and Billingham2008) and Needham (Reference Needham2012), a discussion of which can be found in GNB. In GNB we established that the structure of the solution to this principal free surface flow is characterised in terms of the parameters
$\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
to the horizontal, into or away from a uniform, horizontal strip of inviscid fluid under gravity. This work followed on from that of King & Needham (Reference King and Needham1994), Needham, Billingham & King (Reference Needham, Billingham and King2007), Needham, Chamberlain & Billingham (Reference Needham, Chamberlain and Billingham2008) and Needham (Reference Needham2012), a discussion of which can be found in GNB. In GNB we established that the structure of the solution to this principal free surface flow is characterised in terms of the parameters
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D707}$
(where
$\unicode[STIX]{x1D707}$
(where
![]() $\unicode[STIX]{x1D707}=1+\unicode[STIX]{x1D70E}\tan \unicode[STIX]{x1D6FC}$
, with
$\unicode[STIX]{x1D707}=1+\unicode[STIX]{x1D70E}\tan \unicode[STIX]{x1D6FC}$
, with
![]() $\unicode[STIX]{x1D70E}$
being the dimensionless acceleration of the plate), with a bifurcation in structure as
$\unicode[STIX]{x1D70E}$
being the dimensionless acceleration of the plate), with a bifurcation in structure as
![]() $\unicode[STIX]{x1D707}$
changes sign. This change in local structure leads us to question the well-posedness and stability of the principal flow, and specifically, on short time scales
$\unicode[STIX]{x1D707}$
changes sign. This change in local structure leads us to question the well-posedness and stability of the principal flow, and specifically, on short time scales
![]() $(\ll \sqrt{h/g})$
, with respect to perturbations in the initially horizontal free surface close to the plate contact point and this question is examined in detail in this companion paper to GNB.
$(\ll \sqrt{h/g})$
, with respect to perturbations in the initially horizontal free surface close to the plate contact point and this question is examined in detail in this companion paper to GNB.
The structure of this paper is as follows. In § 2 we formulate the mathematical problem through the introduction of initial perturbations in the horizontal free surface, close to the initial plate contact point. Subsequently §§ 3 and 4 consider the well-posedness and stability of the principal flow (formulated as [IBVP] in GNB) determined by [IBVP] for plates inclined at all angles
![]() $\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
with constant acceleration
$\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
with constant acceleration
![]() $\unicode[STIX]{x1D70E}$
.
$\unicode[STIX]{x1D70E}$
.
Figure 1. Definition sketch showing the displacement of the plate and free surface at time
![]() $t$
.
$t$
.
2 Problem statement
As discussed in the introduction, it is the purpose of this paper to address the well-posedness and stability of the principal flow described in detail in GNB. A definition sketch of the principal flow in GNB is given in figure 1. To this end we adopt all of the notation and terminology established in GNB without repetition (except where it is highlighted by (
![]() $\dagger$
) that a re-definition has been introduced, as, for example, after (3.31)). The principal flow was described in GNB by the initial boundary value problem denoted by [IBVP]. To analyse the well-posedness and stability of the problem [IBVP] with respect to initial perturbations in the horizontal free surface, close to the contact point, we introduce a perturbation on the zero initial data in [IBVP] in the following form, so that the initial conditions in [IBVP] are modified to
$\dagger$
) that a re-definition has been introduced, as, for example, after (3.31)). The principal flow was described in GNB by the initial boundary value problem denoted by [IBVP]. To analyse the well-posedness and stability of the problem [IBVP] with respect to initial perturbations in the horizontal free surface, close to the contact point, we introduce a perturbation on the zero initial data in [IBVP] in the following form, so that the initial conditions in [IBVP] are modified to
with
![]() $0<\unicode[STIX]{x1D6FF}\ll 1$
and
$0<\unicode[STIX]{x1D6FF}\ll 1$
and
![]() $m>0$
, whilst
$m>0$
, whilst
where
![]() $\overline{\unicode[STIX]{x1D702}}_{0}(z)$
is continuous with continuous derivative, and
$\overline{\unicode[STIX]{x1D702}}_{0}(z)$
is continuous with continuous derivative, and
![]() $\overline{\unicode[STIX]{x1D702}}_{0}(0)=\overline{\unicode[STIX]{x1D702}}_{0}(1)=\overline{\unicode[STIX]{x1D702}}_{0,z}(1)=0$
. The form of the initial perturbation is chosen to localise the disturbance in an inner region close to the initial contact point, as it is the main purpose of this paper to examine the rapid localised interaction at the initial contact point between the surface perturbation and its principal development and, since the outer region will be passive in this evolution, the form (2.2) is used to eliminate the need for consideration of a perturbed form of the passive outer problem. The objective of interest is to study the evolution of the perturbation close to the initial contact point, within the innermost regions of the structure of the principal solution to [IBVP], as detailed in GNB. We will choose
$\overline{\unicode[STIX]{x1D702}}_{0}(0)=\overline{\unicode[STIX]{x1D702}}_{0}(1)=\overline{\unicode[STIX]{x1D702}}_{0,z}(1)=0$
. The form of the initial perturbation is chosen to localise the disturbance in an inner region close to the initial contact point, as it is the main purpose of this paper to examine the rapid localised interaction at the initial contact point between the surface perturbation and its principal development and, since the outer region will be passive in this evolution, the form (2.2) is used to eliminate the need for consideration of a perturbed form of the passive outer problem. The objective of interest is to study the evolution of the perturbation close to the initial contact point, within the innermost regions of the structure of the principal solution to [IBVP], as detailed in GNB. We will choose
![]() $m>0$
in (2.1) to achieve this end most effectively. Specifically, the principal flow problem [IBVP] studied in GNB will be referred to as well-posed when the solution to the perturbed problem approaches the solution to [IBVP] as
$m>0$
in (2.1) to achieve this end most effectively. Specifically, the principal flow problem [IBVP] studied in GNB will be referred to as well-posed when the solution to the perturbed problem approaches the solution to [IBVP] as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
, uniformly on
$\unicode[STIX]{x1D6FF}\rightarrow 0$
, uniformly on
![]() ${\mathcal{S}}_{\unicode[STIX]{x1D70F}}=\cup _{\unicode[STIX]{x1D70F}\in [0,T]}(\overline{{\mathcal{D}}}(\unicode[STIX]{x1D70F})\times \{\unicode[STIX]{x1D70F}\})$
for each
${\mathcal{S}}_{\unicode[STIX]{x1D70F}}=\cup _{\unicode[STIX]{x1D70F}\in [0,T]}(\overline{{\mathcal{D}}}(\unicode[STIX]{x1D70F})\times \{\unicode[STIX]{x1D70F}\})$
for each
![]() $T>0$
where
$T>0$
where
![]() $\unicode[STIX]{x1D70F}$
is time scaled on a short time scale associated with
$\unicode[STIX]{x1D70F}$
is time scaled on a short time scale associated with
![]() $\unicode[STIX]{x1D6FF}$
, as given in (3.2) or (4.3). In addition, when [IBVP] is well-posed, we refer to [IBVP] as stable when the solution to the perturbed problem approaches the solution to [IBVP] as
$\unicode[STIX]{x1D6FF}$
, as given in (3.2) or (4.3). In addition, when [IBVP] is well-posed, we refer to [IBVP] as stable when the solution to the perturbed problem approaches the solution to [IBVP] as
![]() $\unicode[STIX]{x1D70F}\rightarrow \infty$
, uniformly in
$\unicode[STIX]{x1D70F}\rightarrow \infty$
, uniformly in
![]() $\overline{{\mathcal{D}}}(\unicode[STIX]{x1D70F})$
; otherwise [IBVP] is said to be unstable. The structure of the solution to [IBVP], as detailed in GNB, determines that there are two cases to consider, which we address in turn. Specifically, as we shall see in what follows, we are interested in the initial dynamics of the flow and free surface close to the initial contact point, and we shall see that this flow develops rapidly on a time scale
$\overline{{\mathcal{D}}}(\unicode[STIX]{x1D70F})$
; otherwise [IBVP] is said to be unstable. The structure of the solution to [IBVP], as detailed in GNB, determines that there are two cases to consider, which we address in turn. Specifically, as we shall see in what follows, we are interested in the initial dynamics of the flow and free surface close to the initial contact point, and we shall see that this flow develops rapidly on a time scale
![]() $t=O(\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x1D6FC}/\unicode[STIX]{x03C0}})$
as
$t=O(\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x1D6FC}/\unicode[STIX]{x03C0}})$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
. Therefore the questions of stability and well-posedness must be addressed on the short time scale
$\unicode[STIX]{x1D6FF}\rightarrow 0$
. Therefore the questions of stability and well-posedness must be addressed on the short time scale
![]() $t=O(\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x1D6FC}/\unicode[STIX]{x03C0}})$
, and, in particular, consider when local (to the initial contact point) well-posedness and stability properties emerge for
$t=O(\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x1D6FC}/\unicode[STIX]{x03C0}})$
, and, in particular, consider when local (to the initial contact point) well-posedness and stability properties emerge for
![]() $t\gg O(\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x1D6FC}/\unicode[STIX]{x03C0}})$
(even though, in the bulk flow
$t\gg O(\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x1D6FC}/\unicode[STIX]{x03C0}})$
(even though, in the bulk flow
![]() $t\ll 1$
). This becomes formally clear in the rescalings that follow.
$t\ll 1$
). This becomes formally clear in the rescalings that follow.
3 The case
 $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in \{(0,\unicode[STIX]{x03C0}/2)\times \mathbb{R}\}\backslash \{(\unicode[STIX]{x03C0}/4,\unicode[STIX]{x03C0}/2)\times \{0\}\}$
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in \{(0,\unicode[STIX]{x03C0}/2)\times \mathbb{R}\}\backslash \{(\unicode[STIX]{x03C0}/4,\unicode[STIX]{x03C0}/2)\times \{0\}\}$
Following an examination of the inner asymptotic regions of [IBVP], as
![]() $t\rightarrow 0^{+}$
, presented in GNB (see GNB (4.1), (4.3) and (4.7)), for the initial perturbation in the free surface to interact with the inner asymptotic region of the solution to [IBVP] as
$t\rightarrow 0^{+}$
, presented in GNB (see GNB (4.1), (4.3) and (4.7)), for the initial perturbation in the free surface to interact with the inner asymptotic region of the solution to [IBVP] as
![]() $t\rightarrow 0^{+}$
, we require
$t\rightarrow 0^{+}$
, we require
![]() $t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}}\sim \unicode[STIX]{x1D6FF}$
and
$t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}}\sim \unicode[STIX]{x1D6FF}$
and
![]() $t^{2}\sim \unicode[STIX]{x1D6FF}^{m}$
, which, as
$t^{2}\sim \unicode[STIX]{x1D6FF}^{m}$
, which, as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
, determines
$\unicode[STIX]{x1D6FF}\rightarrow 0$
, determines
In what follows, we will refer to the initially perturbed modification of [IBVP] as
![]() $\text{[IBVP]}^{\prime }$
, and we will address
$\text{[IBVP]}^{\prime }$
, and we will address
![]() $\text{[IBVP]}^{\prime }$
as
$\text{[IBVP]}^{\prime }$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
with
$\unicode[STIX]{x1D6FF}\rightarrow 0$
with
![]() $t=O(\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x1D6FC}/\unicode[STIX]{x03C0}})$
. Thus we write
$t=O(\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x1D6FC}/\unicode[STIX]{x03C0}})$
. Thus we write
where
![]() $\unicode[STIX]{x1D70F}=O(1)$
as
$\unicode[STIX]{x1D70F}=O(1)$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
. We can now write
$\unicode[STIX]{x1D6FF}\rightarrow 0$
. We can now write
![]() $\text{[IBVP]}^{\prime }$
in terms of
$\text{[IBVP]}^{\prime }$
in terms of
![]() $\overline{x}$
,
$\overline{x}$
,
![]() $y$
,
$y$
,
![]() $\unicode[STIX]{x1D719}$
,
$\unicode[STIX]{x1D719}$
,
![]() $\unicode[STIX]{x1D702}$
,
$\unicode[STIX]{x1D702}$
,
![]() $\unicode[STIX]{x1D70F}$
and
$\unicode[STIX]{x1D70F}$
and
![]() $\unicode[STIX]{x1D6FF}$
, which becomes
$\unicode[STIX]{x1D6FF}$
, which becomes
where
![]() $\unicode[STIX]{x1D702}_{0}:\mathbb{R}\rightarrow \mathbb{R}$
is given by (2.1) and
$\unicode[STIX]{x1D702}_{0}:\mathbb{R}\rightarrow \mathbb{R}$
is given by (2.1) and
![]() $\hat{\boldsymbol{n}}$
is the unit vector normal to the plate pointing into the fluid region. Note that throughout
$\hat{\boldsymbol{n}}$
is the unit vector normal to the plate pointing into the fluid region. Note that throughout
![]() ${\dot{s}}(t)=\unicode[STIX]{x1D70E}t$
and
${\dot{s}}(t)=\unicode[STIX]{x1D70E}t$
and
![]() $\unicode[STIX]{x1D70E}$
has been eliminated in favour of
$\unicode[STIX]{x1D70E}$
has been eliminated in favour of
![]() $\unicode[STIX]{x1D707}$
.
$\unicode[STIX]{x1D707}$
.
The structure of the solution to [IBVP] as
![]() $t\rightarrow 0^{+}$
(as discussed in GNB) indicates that there will be two asymptotic regions in the solution to
$t\rightarrow 0^{+}$
(as discussed in GNB) indicates that there will be two asymptotic regions in the solution to
![]() $\text{[IBVP]}^{\prime }$
as
$\text{[IBVP]}^{\prime }$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
when
$\unicode[STIX]{x1D6FF}\rightarrow 0$
when
![]() $\unicode[STIX]{x1D70F}=O(1)$
. In the outer asymptotic region we have
$\unicode[STIX]{x1D70F}=O(1)$
. In the outer asymptotic region we have
![]() $(\overline{x},y)(\in \overline{{\mathcal{D}}}(\unicode[STIX]{x1D70F}))=O(1)$
and
$(\overline{x},y)(\in \overline{{\mathcal{D}}}(\unicode[STIX]{x1D70F}))=O(1)$
and
![]() $\unicode[STIX]{x1D70F}=O(1)$
as
$\unicode[STIX]{x1D70F}=O(1)$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
, and we consider this first.
$\unicode[STIX]{x1D6FF}\rightarrow 0$
, and we consider this first.
3.1 Outer region for
 $\text{[IBVP]}^{\prime }$
when
$\text{[IBVP]}^{\prime }$
when
 $\unicode[STIX]{x1D70F}=O(1)$
as
$\unicode[STIX]{x1D70F}=O(1)$
as
 $\unicode[STIX]{x1D6FF}\rightarrow 0$
$\unicode[STIX]{x1D6FF}\rightarrow 0$
We begin in an outer region in which
![]() $(\overline{x},y)(\in \overline{{\mathcal{D}}}(\unicode[STIX]{x1D70F}))=O(1)$
and
$(\overline{x},y)(\in \overline{{\mathcal{D}}}(\unicode[STIX]{x1D70F}))=O(1)$
and
![]() $\unicode[STIX]{x1D70F}=O(1)$
as
$\unicode[STIX]{x1D70F}=O(1)$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
, after which we will require an inner region, in which
$\unicode[STIX]{x1D6FF}\rightarrow 0$
, after which we will require an inner region, in which
![]() $(\overline{x},y)=o(1)$
and
$(\overline{x},y)=o(1)$
and
![]() $\unicode[STIX]{x1D70F}=O(1)$
as
$\unicode[STIX]{x1D70F}=O(1)$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
, in order to capture the initial interaction between the plate and the perturbed fluid free surface. We first observe that the initial conditions (3.11) and (3.12) require that
$\unicode[STIX]{x1D6FF}\rightarrow 0$
, in order to capture the initial interaction between the plate and the perturbed fluid free surface. We first observe that the initial conditions (3.11) and (3.12) require that
![]() $\unicode[STIX]{x1D702}$
,
$\unicode[STIX]{x1D702}$
,
![]() $\unicode[STIX]{x1D719}=o(1)$
as
$\unicode[STIX]{x1D719}=o(1)$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
in the outer region. Specifically, conditions (3.4) and (3.6) require that
$\unicode[STIX]{x1D6FF}\rightarrow 0$
in the outer region. Specifically, conditions (3.4) and (3.6) require that
![]() $\unicode[STIX]{x1D719}=O(\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x1D6FC}/\unicode[STIX]{x03C0}})$
and
$\unicode[STIX]{x1D719}=O(\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x1D6FC}/\unicode[STIX]{x03C0}})$
and
![]() $\unicode[STIX]{x1D702}=O(\unicode[STIX]{x1D6FF}^{2\unicode[STIX]{x1D6FC}/\unicode[STIX]{x03C0}})$
as
$\unicode[STIX]{x1D702}=O(\unicode[STIX]{x1D6FF}^{2\unicode[STIX]{x1D6FC}/\unicode[STIX]{x03C0}})$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
. Thus we introduce the asymptotic expansions
$\unicode[STIX]{x1D6FF}\rightarrow 0$
. Thus we introduce the asymptotic expansions
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
in the outer region, with the factor
$\unicode[STIX]{x1D6FF}\rightarrow 0$
in the outer region, with the factor
![]() $(\unicode[STIX]{x1D707}-1)\cos \unicode[STIX]{x1D6FC}$
in (3.13) included for algebraic convenience at a later stage. Here we note that the notation
$(\unicode[STIX]{x1D707}-1)\cos \unicode[STIX]{x1D6FC}$
in (3.13) included for algebraic convenience at a later stage. Here we note that the notation
![]() $^{\prime }$
is not to be confused with the indication of dimensionality in GNB, nor does it refer to differentiation. Substituting the expansions (3.13) and (3.14) into
$^{\prime }$
is not to be confused with the indication of dimensionality in GNB, nor does it refer to differentiation. Substituting the expansions (3.13) and (3.14) into
![]() $\text{[IBVP]}^{\prime }$
, we obtain the leading-order evolution problem in the outer region for
$\text{[IBVP]}^{\prime }$
, we obtain the leading-order evolution problem in the outer region for
![]() $\unicode[STIX]{x1D719}^{\prime }$
, namely
$\unicode[STIX]{x1D719}^{\prime }$
, namely
with
![]() $\unicode[STIX]{x1D702}^{\prime }$
then given by
$\unicode[STIX]{x1D702}^{\prime }$
then given by
Note that the free surface perturbation is absent in (3.22) as the perturbation is localised in the inner region. We next introduce
![]() $\overline{\unicode[STIX]{x1D719}}^{\prime }(\overline{x},y)$
and
$\overline{\unicode[STIX]{x1D719}}^{\prime }(\overline{x},y)$
and
![]() $\overline{\unicode[STIX]{x1D702}}^{\prime }(\overline{x})$
by writing
$\overline{\unicode[STIX]{x1D702}}^{\prime }(\overline{x})$
by writing
The resulting problem for
![]() $\overline{\unicode[STIX]{x1D719}}^{\prime }$
and
$\overline{\unicode[STIX]{x1D719}}^{\prime }$
and
![]() $\overline{\unicode[STIX]{x1D702}}^{\prime }$
, obtained after substituting (3.23) into (3.15)–(3.22), is the same as the outer region problem which was solved and discussed in GNB, and as such details are omitted here. We thus have that
$\overline{\unicode[STIX]{x1D702}}^{\prime }$
, obtained after substituting (3.23) into (3.15)–(3.22), is the same as the outer region problem which was solved and discussed in GNB, and as such details are omitted here. We thus have that
![]() $\overline{\unicode[STIX]{x1D719}}^{\prime }$
is given, for some real constants
$\overline{\unicode[STIX]{x1D719}}^{\prime }$
is given, for some real constants
![]() $A_{n}$
,
$A_{n}$
,
![]() $B_{n}$
and
$B_{n}$
and
![]() $C_{n}(n=0,1,2,\ldots )$
, by
$C_{n}(n=0,1,2,\ldots )$
, by
for
![]() $0\leqslant r<\text{cosec}\,\unicode[STIX]{x1D6FC}$
,
$0\leqslant r<\text{cosec}\,\unicode[STIX]{x1D6FC}$
,
![]() $-\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D703}\leqslant 0$
, where
$-\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D703}\leqslant 0$
, where
![]() $\overline{x}=r\cos \unicode[STIX]{x1D703}$
and
$\overline{x}=r\cos \unicode[STIX]{x1D703}$
and
![]() $y=r\sin \unicode[STIX]{x1D703}$
, whilst
$y=r\sin \unicode[STIX]{x1D703}$
, whilst
for
![]() $0\leqslant \unicode[STIX]{x1D70C}<1$
,
$0\leqslant \unicode[STIX]{x1D70C}<1$
,
![]() $0\leqslant \overline{\unicode[STIX]{x1D703}}\leqslant \unicode[STIX]{x03C0}-\unicode[STIX]{x1D6FC}$
, where
$0\leqslant \overline{\unicode[STIX]{x1D703}}\leqslant \unicode[STIX]{x03C0}-\unicode[STIX]{x1D6FC}$
, where
![]() $\overline{x}-\cot \unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D70C}\cos \overline{\unicode[STIX]{x1D703}}$
, and
$\overline{x}-\cot \unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D70C}\cos \overline{\unicode[STIX]{x1D703}}$
, and
![]() $y+1=\unicode[STIX]{x1D70C}\sin \overline{\unicode[STIX]{x1D703}}$
, and finally
$y+1=\unicode[STIX]{x1D70C}\sin \overline{\unicode[STIX]{x1D703}}$
, and finally
for
![]() $\overline{x}>\cot \unicode[STIX]{x1D6FC}$
,
$\overline{x}>\cot \unicode[STIX]{x1D6FC}$
,
![]() $-1\leqslant y\leqslant 0$
. It then follows from (3.21), (3.24) and (3.26), that
$-1\leqslant y\leqslant 0$
. It then follows from (3.21), (3.24) and (3.26), that
for
![]() $0\leqslant \overline{x}<\text{cosec}\,\unicode[STIX]{x1D6FC}$
, and
$0\leqslant \overline{x}<\text{cosec}\,\unicode[STIX]{x1D6FC}$
, and
for
![]() $\overline{x}\geqslant \text{cosec}\,\unicode[STIX]{x1D6FC}$
. We observe from (3.24) and (3.27) that, as
$\overline{x}\geqslant \text{cosec}\,\unicode[STIX]{x1D6FC}$
. We observe from (3.24) and (3.27) that, as
![]() $(\overline{x},y)\rightarrow (0,0)$
,
$(\overline{x},y)\rightarrow (0,0)$
,
 $$\begin{eqnarray}\displaystyle \overline{\unicode[STIX]{x1D719}}^{\prime }(r,\unicode[STIX]{x1D703}) & = & \displaystyle \frac{r\sin \unicode[STIX]{x1D703}}{\cos \unicode[STIX]{x1D6FC}}+A_{0}(\unicode[STIX]{x1D6FC})r^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}}\sin \frac{\unicode[STIX]{x03C0}\unicode[STIX]{x1D703}}{2\unicode[STIX]{x1D6FC}}+O(r^{3\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}}),\nonumber\\ \displaystyle & & \displaystyle \quad \text{as }r\rightarrow 0^{+},\text{ with }-\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D703}\leqslant 0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \overline{\unicode[STIX]{x1D719}}^{\prime }(r,\unicode[STIX]{x1D703}) & = & \displaystyle \frac{r\sin \unicode[STIX]{x1D703}}{\cos \unicode[STIX]{x1D6FC}}+A_{0}(\unicode[STIX]{x1D6FC})r^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}}\sin \frac{\unicode[STIX]{x03C0}\unicode[STIX]{x1D703}}{2\unicode[STIX]{x1D6FC}}+O(r^{3\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}}),\nonumber\\ \displaystyle & & \displaystyle \quad \text{as }r\rightarrow 0^{+},\text{ with }-\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D703}\leqslant 0,\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \overline{\unicode[STIX]{x1D702}}^{\prime }(\overline{x}) & = & \displaystyle \frac{1}{2}(\unicode[STIX]{x1D707}-1)+A_{0}(\unicode[STIX]{x1D6FC})\frac{\unicode[STIX]{x03C0}}{4\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D707}-1)\cos \unicode[STIX]{x1D6FC}\overline{x}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-1}+O(\overline{x}^{3\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-1}),\nonumber\\ \displaystyle & & \displaystyle \quad \text{as }\overline{x}\rightarrow 0^{+},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \overline{\unicode[STIX]{x1D702}}^{\prime }(\overline{x}) & = & \displaystyle \frac{1}{2}(\unicode[STIX]{x1D707}-1)+A_{0}(\unicode[STIX]{x1D6FC})\frac{\unicode[STIX]{x03C0}}{4\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D707}-1)\cos \unicode[STIX]{x1D6FC}\overline{x}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-1}+O(\overline{x}^{3\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-1}),\nonumber\\ \displaystyle & & \displaystyle \quad \text{as }\overline{x}\rightarrow 0^{+},\end{eqnarray}$$
where
![]() $r$
and
$r$
and
![]() $\unicode[STIX]{x1D703}$
are the polar coordinates defined above, and
$\unicode[STIX]{x1D703}$
are the polar coordinates defined above, and
![]() $A_{0}(\unicode[STIX]{x1D6FC})({<}\!0)$
as given in GNB (see GNB (3.10)). Equation (3.30) reveals a weak singularity in
$A_{0}(\unicode[STIX]{x1D6FC})({<}\!0)$
as given in GNB (see GNB (3.10)). Equation (3.30) reveals a weak singularity in
![]() $\overline{\unicode[STIX]{x1D702}}_{\overline{x}}^{\prime }(\overline{x})$
as
$\overline{\unicode[STIX]{x1D702}}_{\overline{x}}^{\prime }(\overline{x})$
as
![]() $\overline{x}\rightarrow 0^{+}$
. This singular behaviour as
$\overline{x}\rightarrow 0^{+}$
. This singular behaviour as
![]() $\overline{x}\rightarrow 0^{+}$
is compounded in higher-order terms in the outer expansions (3.13) and (3.14), and so the regularity conditions (see GNB (2.16)) fail to be satisfied by the outer region asymptotic expansions in a neighbourhood of the initial intersection point of the plate and the free surface, where
$\overline{x}\rightarrow 0^{+}$
is compounded in higher-order terms in the outer expansions (3.13) and (3.14), and so the regularity conditions (see GNB (2.16)) fail to be satisfied by the outer region asymptotic expansions in a neighbourhood of the initial intersection point of the plate and the free surface, where
![]() $(\overline{x},y)=o(1)$
as
$(\overline{x},y)=o(1)$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
. Therefore, in order to capture the full regularity in the neighbourhood of the intersection point of the plate and the free surface, the introduction of an inner region is required.
$\unicode[STIX]{x1D6FF}\rightarrow 0$
. Therefore, in order to capture the full regularity in the neighbourhood of the intersection point of the plate and the free surface, the introduction of an inner region is required.
3.2 Inner region for
 $\text{[IBVP]}^{\prime }$
when
$\text{[IBVP]}^{\prime }$
when
 $\unicode[STIX]{x1D70F}=O(1)$
as
$\unicode[STIX]{x1D70F}=O(1)$
as
 $\unicode[STIX]{x1D6FF}\rightarrow 0$
$\unicode[STIX]{x1D6FF}\rightarrow 0$
We have
![]() $(\overline{x},y)=O(\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF}))$
, with
$(\overline{x},y)=O(\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF}))$
, with
![]() $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})=o(1)$
as
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})=o(1)$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
in the inner region. It then follows from (3.14), (3.23) and (3.30) that
$\unicode[STIX]{x1D6FF}\rightarrow 0$
in the inner region. It then follows from (3.14), (3.23) and (3.30) that
![]() $\unicode[STIX]{x1D702}=O(\unicode[STIX]{x1D6FF}^{2\unicode[STIX]{x1D6FC}/\unicode[STIX]{x03C0}})$
as
$\unicode[STIX]{x1D702}=O(\unicode[STIX]{x1D6FF}^{2\unicode[STIX]{x1D6FC}/\unicode[STIX]{x03C0}})$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
in the inner region, so that, to capture the free surface in the inner region, we must take
$\unicode[STIX]{x1D6FF}\rightarrow 0$
in the inner region, so that, to capture the free surface in the inner region, we must take
![]() $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})=O(\unicode[STIX]{x1D6FF}^{2\unicode[STIX]{x1D6FC}/\unicode[STIX]{x03C0}})$
as
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})=O(\unicode[STIX]{x1D6FF}^{2\unicode[STIX]{x1D6FC}/\unicode[STIX]{x03C0}})$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
; therefore, without loss of generality, we set
$\unicode[STIX]{x1D6FF}\rightarrow 0$
; therefore, without loss of generality, we set
![]() $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})=\unicode[STIX]{x1D6FF}^{2\unicode[STIX]{x1D6FC}/\unicode[STIX]{x03C0}}$
. An examination of (3.13), (3.23), and (3.29) then requires that
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})=\unicode[STIX]{x1D6FF}^{2\unicode[STIX]{x1D6FC}/\unicode[STIX]{x03C0}}$
. An examination of (3.13), (3.23), and (3.29) then requires that
![]() $\unicode[STIX]{x1D719}=O(\unicode[STIX]{x1D6FF}^{2\unicode[STIX]{x1D6FC}/\unicode[STIX]{x03C0}})$
as
$\unicode[STIX]{x1D719}=O(\unicode[STIX]{x1D6FF}^{2\unicode[STIX]{x1D6FC}/\unicode[STIX]{x03C0}})$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
in the inner region. Thus we introduce scaled inner region coordinates
$\unicode[STIX]{x1D6FF}\rightarrow 0$
in the inner region. Thus we introduce scaled inner region coordinates
![]() $(X,Y)$
by
$(X,Y)$
by
with
![]() $(X,Y)=O(1)$
as
$(X,Y)=O(1)$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
(
$\unicode[STIX]{x1D6FF}\rightarrow 0$
(
![]() $\dagger$
). The plate is located in the inner region at
$\dagger$
). The plate is located in the inner region at
![]() $Y=-X\tan \unicode[STIX]{x1D6FC}$
, with the contact point denoted by
$Y=-X\tan \unicode[STIX]{x1D6FC}$
, with the contact point denoted by
![]() $(X,Y)=(X_{p}(\unicode[STIX]{x1D70F}),Y_{p}(\unicode[STIX]{x1D70F}))$
, where
$(X,Y)=(X_{p}(\unicode[STIX]{x1D70F}),Y_{p}(\unicode[STIX]{x1D70F}))$
, where
![]() $\overline{x}_{p}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D6FF}^{2\unicode[STIX]{x1D6FC}/\unicode[STIX]{x03C0}}X_{p}(\unicode[STIX]{x1D70F})$
and
$\overline{x}_{p}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D6FF}^{2\unicode[STIX]{x1D6FC}/\unicode[STIX]{x03C0}}X_{p}(\unicode[STIX]{x1D70F})$
and
![]() $y_{p}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D6FF}^{2\unicode[STIX]{x1D6FC}/\unicode[STIX]{x03C0}}Y_{p}(\unicode[STIX]{x1D70F})$
(
$y_{p}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D6FF}^{2\unicode[STIX]{x1D6FC}/\unicode[STIX]{x03C0}}Y_{p}(\unicode[STIX]{x1D70F})$
(
![]() $\dagger$
). We now write the free surface and velocity potential in the inner region as
$\dagger$
). We now write the free surface and velocity potential in the inner region as
where
![]() $\unicode[STIX]{x1D702}_{I}(X,\unicode[STIX]{x1D70F})$
,
$\unicode[STIX]{x1D702}_{I}(X,\unicode[STIX]{x1D70F})$
,
![]() $\unicode[STIX]{x1D719}_{I}(X,Y,\unicode[STIX]{x1D70F})=O(1)$
as
$\unicode[STIX]{x1D719}_{I}(X,Y,\unicode[STIX]{x1D70F})=O(1)$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
(
$\unicode[STIX]{x1D6FF}\rightarrow 0$
(
![]() $\dagger$
). The inner region expansions are introduced as
$\dagger$
). The inner region expansions are introduced as
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
with
$\unicode[STIX]{x1D6FF}\rightarrow 0$
with
![]() $(X,Y)=O(1)$
, where the form of the correction terms have been deduced from (3.31), together with (3.14), (3.23) and (3.30). It follows from (3.31) and (3.34) that the free surface in the inner region is located at
$(X,Y)=O(1)$
, where the form of the correction terms have been deduced from (3.31), together with (3.14), (3.23) and (3.30). It follows from (3.31) and (3.34) that the free surface in the inner region is located at
Hence we must expand
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
, after which
$\unicode[STIX]{x1D6FF}\rightarrow 0$
, after which
![]() $Y_{p}(\unicode[STIX]{x1D70F})=-X_{p}(\unicode[STIX]{x1D70F})\tan \unicode[STIX]{x1D6FC}$
(
$Y_{p}(\unicode[STIX]{x1D70F})=-X_{p}(\unicode[STIX]{x1D70F})\tan \unicode[STIX]{x1D6FC}$
(
![]() $\dagger$
).
$\dagger$
).
We now write
![]() $\text{[IBVP]}^{\prime }$
in terms of the inner variables and substitute from (3.34) and (3.35). The problem obtained at leading order, when supplemented with matching conditions to the outer region (obtained through Van Dyke’s matching principle (Van Dyke Reference Van Dyke1964)), has the solution
$\text{[IBVP]}^{\prime }$
in terms of the inner variables and substitute from (3.34) and (3.35). The problem obtained at leading order, when supplemented with matching conditions to the outer region (obtained through Van Dyke’s matching principle (Van Dyke Reference Van Dyke1964)), has the solution
It follows from (3.38) and (3.39), with (3.31)–(3.35), that the regularity conditions (see GNB (2.16)) are satisfied at leading order in the inner region. We now formulate the problem at
![]() $O(\unicode[STIX]{x1D6FF}^{1-2\unicode[STIX]{x1D6FC}/\unicode[STIX]{x03C0}})$
, where it is convenient to introduce the coordinates
$O(\unicode[STIX]{x1D6FF}^{1-2\unicode[STIX]{x1D6FC}/\unicode[STIX]{x03C0}})$
, where it is convenient to introduce the coordinates
![]() $(\overline{X},\overline{Y})$
as
$(\overline{X},\overline{Y})$
as
which is simply a shift of origin from the original inner coordinates
![]() $(X,Y)$
. We next write
$(X,Y)$
. We next write
where
![]() $\widetilde{\unicode[STIX]{x1D702}}_{1}^{\prime }|_{0}$
and
$\widetilde{\unicode[STIX]{x1D702}}_{1}^{\prime }|_{0}$
and
![]() $\widetilde{\unicode[STIX]{x1D719}}_{1}^{\prime }|_{0}$
are given by
$\widetilde{\unicode[STIX]{x1D719}}_{1}^{\prime }|_{0}$
are given by
 $$\begin{eqnarray}\displaystyle \widetilde{\unicode[STIX]{x1D719}}_{1}^{\prime }(\overline{X},\overline{Y},\unicode[STIX]{x1D70F})|_{0} & = & \displaystyle A_{0}(\unicode[STIX]{x1D6FC})(\unicode[STIX]{x1D707}-1)\cos \unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70F}^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}\widehat{\unicode[STIX]{x1D719}}\left(\frac{\overline{X}}{\unicode[STIX]{x1D70F}^{2}},\frac{\overline{Y}}{\unicode[STIX]{x1D70F}^{2}}\right),\nonumber\\ \displaystyle & & \displaystyle \quad \overline{X}\geqslant 0,-\overline{X}\tan \unicode[STIX]{x1D6FC}\leqslant \overline{Y}\leqslant 0,\unicode[STIX]{x1D70F}>0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widetilde{\unicode[STIX]{x1D719}}_{1}^{\prime }(\overline{X},\overline{Y},\unicode[STIX]{x1D70F})|_{0} & = & \displaystyle A_{0}(\unicode[STIX]{x1D6FC})(\unicode[STIX]{x1D707}-1)\cos \unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70F}^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}\widehat{\unicode[STIX]{x1D719}}\left(\frac{\overline{X}}{\unicode[STIX]{x1D70F}^{2}},\frac{\overline{Y}}{\unicode[STIX]{x1D70F}^{2}}\right),\nonumber\\ \displaystyle & & \displaystyle \quad \overline{X}\geqslant 0,-\overline{X}\tan \unicode[STIX]{x1D6FC}\leqslant \overline{Y}\leqslant 0,\unicode[STIX]{x1D70F}>0,\end{eqnarray}$$
and
![]() $\widehat{\unicode[STIX]{x1D702}}$
and
$\widehat{\unicode[STIX]{x1D702}}$
and
![]() $\widehat{\unicode[STIX]{x1D719}}$
are solutions to the boundary value problem in GNB (see (3.10)–(4.16)) when written in the similarity coordinates
$\widehat{\unicode[STIX]{x1D719}}$
are solutions to the boundary value problem in GNB (see (3.10)–(4.16)) when written in the similarity coordinates
![]() $(\overline{X},\overline{Y})\rightarrow \unicode[STIX]{x1D70F}^{-2}(\overline{X},\overline{Y})$
. Rewriting the problem at
$(\overline{X},\overline{Y})\rightarrow \unicode[STIX]{x1D70F}^{-2}(\overline{X},\overline{Y})$
. Rewriting the problem at
![]() $O(\unicode[STIX]{x1D6FF}^{1-2\unicode[STIX]{x1D6FC}/\unicode[STIX]{x03C0}})$
in terms of
$O(\unicode[STIX]{x1D6FF}^{1-2\unicode[STIX]{x1D6FC}/\unicode[STIX]{x03C0}})$
in terms of
![]() $H^{\prime }$
and
$H^{\prime }$
and
![]() $\unicode[STIX]{x1D6F7}^{\prime }$
we obtain
$\unicode[STIX]{x1D6F7}^{\prime }$
we obtain
Here
![]() $\overline{\unicode[STIX]{x1D735}}=(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\overline{X},\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\overline{Y})$
and we have, for convenience, introduced polar coordinates
$\overline{\unicode[STIX]{x1D735}}=(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\overline{X},\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\overline{Y})$
and we have, for convenience, introduced polar coordinates
![]() $(\overline{R},\unicode[STIX]{x1D703})$
, given by
$(\overline{R},\unicode[STIX]{x1D703})$
, given by
![]() $\overline{X}=\overline{R}\cos \unicode[STIX]{x1D703}$
,
$\overline{X}=\overline{R}\cos \unicode[STIX]{x1D703}$
,
![]() $\overline{Y}=\overline{R}\sin \unicode[STIX]{x1D703}$
(
$\overline{Y}=\overline{R}\sin \unicode[STIX]{x1D703}$
(
![]() $\dagger$
). We begin our investigation of the problem (3.45)–(3.52) in the case
$\dagger$
). We begin our investigation of the problem (3.45)–(3.52) in the case
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,\unicode[STIX]{x03C0}/2)\times (\mathbb{R}\backslash \{0\})$
. We seek solutions of the form
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,\unicode[STIX]{x03C0}/2)\times (\mathbb{R}\backslash \{0\})$
. We seek solutions of the form
where
![]() $\unicode[STIX]{x1D706}\in \mathbb{C}$
, which leads to a decoupled linear harmonic boundary value problem for
$\unicode[STIX]{x1D706}\in \mathbb{C}$
, which leads to a decoupled linear harmonic boundary value problem for
![]() $\overline{\unicode[STIX]{x1D6F7}}^{\prime }$
, given by
$\overline{\unicode[STIX]{x1D6F7}}^{\prime }$
, given by
where
![]() $k=-\unicode[STIX]{x1D706}^{2}/\unicode[STIX]{x1D707}$
(for
$k=-\unicode[STIX]{x1D706}^{2}/\unicode[STIX]{x1D707}$
(for
![]() $\unicode[STIX]{x1D707}\neq 0$
). Although unnecessary, if required we obtain
$\unicode[STIX]{x1D707}\neq 0$
). Although unnecessary, if required we obtain
![]() $\overline{H}^{\prime }$
from
$\overline{H}^{\prime }$
from
Here, according to the regularity conditions (see GNB (2.16)), we require that solutions to (3.54)–(3.57),
![]() $\overline{\unicode[STIX]{x1D6F7}}^{\prime }:\overline{{\mathcal{G}}}_{\infty }\rightarrow \mathbb{C}$
, have regularity
$\overline{\unicode[STIX]{x1D6F7}}^{\prime }:\overline{{\mathcal{G}}}_{\infty }\rightarrow \mathbb{C}$
, have regularity
where
The linear harmonic problem (3.54)–(3.57) is a spectral problem with spectral parameter
![]() $k\in \mathbb{C}$
. We henceforth refer to this spectral problem as [SP
$k\in \mathbb{C}$
. We henceforth refer to this spectral problem as [SP
![]() $(k)$
]. It is clear that [SP
$(k)$
]. It is clear that [SP
![]() $(k)$
] has the trivial solution for each
$(k)$
] has the trivial solution for each
![]() $k\in \mathbb{C}$
. Further, let
$k\in \mathbb{C}$
. Further, let
![]() $\overline{\unicode[STIX]{x1D6F7}}_{k}^{\prime }:{\mathcal{G}}_{\infty }\rightarrow \mathbb{C}$
be a non-trivial solution to [SP
$\overline{\unicode[STIX]{x1D6F7}}_{k}^{\prime }:{\mathcal{G}}_{\infty }\rightarrow \mathbb{C}$
be a non-trivial solution to [SP
![]() $(k)$
], then it is straightforward to establish the following.
$(k)$
], then it is straightforward to establish the following.
-
(i) When
 $k\in \mathbb{R}^{+}$
(3.61)as
$k\in \mathbb{R}^{+}$
(3.61)as $$\begin{eqnarray}\displaystyle \overline{\unicode[STIX]{x1D6F7}}_{k}^{\prime }(\overline{R},\unicode[STIX]{x1D703}) & = & \displaystyle (c_{k}\text{e}^{\text{i}k\overline{R}\cos \unicode[STIX]{x1D703}}+d_{k}\text{e}^{-\text{i}k\overline{R}\cos \unicode[STIX]{x1D703}})\text{e}^{k\overline{R}\sin \unicode[STIX]{x1D703}}\nonumber\\ \displaystyle & & \displaystyle +\,a_{k}\frac{1}{\overline{R}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}}}\sin \frac{\unicode[STIX]{x03C0}}{2\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D703}+O\left(\frac{1}{\overline{R}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}+1}}\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \overline{\unicode[STIX]{x1D6F7}}_{k}^{\prime }(\overline{R},\unicode[STIX]{x1D703}) & = & \displaystyle (c_{k}\text{e}^{\text{i}k\overline{R}\cos \unicode[STIX]{x1D703}}+d_{k}\text{e}^{-\text{i}k\overline{R}\cos \unicode[STIX]{x1D703}})\text{e}^{k\overline{R}\sin \unicode[STIX]{x1D703}}\nonumber\\ \displaystyle & & \displaystyle +\,a_{k}\frac{1}{\overline{R}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}}}\sin \frac{\unicode[STIX]{x03C0}}{2\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D703}+O\left(\frac{1}{\overline{R}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}+1}}\right),\end{eqnarray}$$
 $\overline{R}\rightarrow \infty$
uniformly for
$\overline{R}\rightarrow \infty$
uniformly for
 $-\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D703}\leqslant 0$
. Here,
$-\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D703}\leqslant 0$
. Here,
 $c_{k}$
,
$c_{k}$
,
 $d_{k}$
,
$d_{k}$
,
 $a_{k}\in \mathbb{C}$
are not all zero constants.
$a_{k}\in \mathbb{C}$
are not all zero constants.
-
(ii) When
 $k=0$
(3.62)as
$k=0$
(3.62)as $$\begin{eqnarray}\overline{\unicode[STIX]{x1D6F7}}_{0}^{\prime }(\overline{R},\unicode[STIX]{x1D703})=a_{0}+b_{0}\frac{1}{\overline{R}^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}}}\cos \frac{\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D703}+O\left(\frac{1}{\overline{R}^{2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}}}\right),\end{eqnarray}$$
$$\begin{eqnarray}\overline{\unicode[STIX]{x1D6F7}}_{0}^{\prime }(\overline{R},\unicode[STIX]{x1D703})=a_{0}+b_{0}\frac{1}{\overline{R}^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}}}\cos \frac{\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D703}+O\left(\frac{1}{\overline{R}^{2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}}}\right),\end{eqnarray}$$
 $\overline{R}\rightarrow \infty$
uniformly for
$\overline{R}\rightarrow \infty$
uniformly for
 $-\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D703}\leqslant 0$
. Here
$-\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D703}\leqslant 0$
. Here
 $a_{0}$
,
$a_{0}$
,
 $b_{0}\in \mathbb{C}$
are not both zero constants.
$b_{0}\in \mathbb{C}$
are not both zero constants.
-
(iii) When
 $k\in \mathbb{C}\backslash (\mathbb{R}^{+}\cup \{0\})$
(3.63)as
$k\in \mathbb{C}\backslash (\mathbb{R}^{+}\cup \{0\})$
(3.63)as $$\begin{eqnarray}\overline{\unicode[STIX]{x1D6F7}}_{k}^{\prime }(\overline{R},\unicode[STIX]{x1D703})=a_{k}\frac{1}{\overline{R}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}}}\sin \frac{\unicode[STIX]{x03C0}}{2\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D703}+O\left(\frac{1}{\overline{R}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}+1}}\right),\end{eqnarray}$$
$$\begin{eqnarray}\overline{\unicode[STIX]{x1D6F7}}_{k}^{\prime }(\overline{R},\unicode[STIX]{x1D703})=a_{k}\frac{1}{\overline{R}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}}}\sin \frac{\unicode[STIX]{x03C0}}{2\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D703}+O\left(\frac{1}{\overline{R}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}+1}}\right),\end{eqnarray}$$
 $\overline{R}\rightarrow \infty$
uniformly for
$\overline{R}\rightarrow \infty$
uniformly for
 $-\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D703}\leqslant 0$
. Here,
$-\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D703}\leqslant 0$
. Here,
 $a_{k}\in \mathbb{C}$
is a non-zero constant.
$a_{k}\in \mathbb{C}$
is a non-zero constant.
Our objective now is to classify the spectrum of [SP
![]() $(k)$
]. We define the spectrum of [SP
$(k)$
]. We define the spectrum of [SP
![]() $(k)$
] to be
$(k)$
] to be
![]() $\boldsymbol{S}$
, where
$\boldsymbol{S}$
, where
The set of eigenvalues of [SP
![]() $(k)$
] is
$(k)$
] is
![]() $\boldsymbol{S}^{d}$
, where
$\boldsymbol{S}^{d}$
, where
and the continuous spectrum of [SP
![]() $(k)$
] is
$(k)$
] is
![]() $\boldsymbol{S}^{c}$
, where
$\boldsymbol{S}^{c}$
, where
with the limits as
![]() $\overline{R}\rightarrow \infty$
considered as uniform for
$\overline{R}\rightarrow \infty$
considered as uniform for
![]() $-\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D703}\leqslant 0$
. We observe that
$-\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D703}\leqslant 0$
. We observe that
Following Needham (Reference Needham2012), together with the use of (3.61)–(3.63) above we can establish that (see appendix A)
and so
We now introduce
![]() $\boldsymbol{S}_{\unicode[STIX]{x1D706}}\subseteq \mathbb{C}$
, where
$\boldsymbol{S}_{\unicode[STIX]{x1D706}}\subseteq \mathbb{C}$
, where
Following (3.69), for
![]() $\unicode[STIX]{x1D707}>0$
, we have
$\unicode[STIX]{x1D707}>0$
, we have
and, for
![]() $\unicode[STIX]{x1D707}<0$
, we have
$\unicode[STIX]{x1D707}<0$
, we have
Now, the linear evolution problem (3.45)–(3.52) has a solution represented as a Fourier type integral with respect to
![]() $\unicode[STIX]{x1D706}$
over the elementary solutions (3.53), with
$\unicode[STIX]{x1D706}$
over the elementary solutions (3.53), with
![]() $\unicode[STIX]{x1D706}\in \boldsymbol{S}_{\unicode[STIX]{x1D706}}^{+}$
(
$\unicode[STIX]{x1D706}\in \boldsymbol{S}_{\unicode[STIX]{x1D706}}^{+}$
(
![]() $\unicode[STIX]{x1D707}>0$
) or
$\unicode[STIX]{x1D707}>0$
) or
![]() $\unicode[STIX]{x1D706}\in \boldsymbol{S}_{\unicode[STIX]{x1D706}}^{-}$
(
$\unicode[STIX]{x1D706}\in \boldsymbol{S}_{\unicode[STIX]{x1D706}}^{-}$
(
![]() $\unicode[STIX]{x1D707}<0$
) and density functions chosen to satisfy the initial conditions (3.51) and (3.52). We conclude that the linear evolution problem (3.45)–(3.52) is:
$\unicode[STIX]{x1D707}<0$
) and density functions chosen to satisfy the initial conditions (3.51) and (3.52). We conclude that the linear evolution problem (3.45)–(3.52) is:
-
(i) well-posed and stable when
 $\text{Re}(\unicode[STIX]{x1D706})\geqslant 0$
for all
$\text{Re}(\unicode[STIX]{x1D706})\geqslant 0$
for all
 $\unicode[STIX]{x1D706}\in \boldsymbol{S}_{\unicode[STIX]{x1D706}}$
;
$\unicode[STIX]{x1D706}\in \boldsymbol{S}_{\unicode[STIX]{x1D706}}$
; -
(ii) well-posed and unstable when there exists
 $M\in \mathbb{R}$
such that
$M\in \mathbb{R}$
such that
 $\text{Re}(\unicode[STIX]{x1D706})\geqslant M$
for all
$\text{Re}(\unicode[STIX]{x1D706})\geqslant M$
for all
 $\unicode[STIX]{x1D706}\in \boldsymbol{S}_{\unicode[STIX]{x1D706}}$
, and there exists
$\unicode[STIX]{x1D706}\in \boldsymbol{S}_{\unicode[STIX]{x1D706}}$
, and there exists
 $\unicode[STIX]{x1D706}^{\ast }\in \boldsymbol{S}_{\unicode[STIX]{x1D706}}$
such that
$\unicode[STIX]{x1D706}^{\ast }\in \boldsymbol{S}_{\unicode[STIX]{x1D706}}$
such that
 $\text{Re}(\unicode[STIX]{x1D706}^{\ast })<0$
;
$\text{Re}(\unicode[STIX]{x1D706}^{\ast })<0$
; -
(iii) ill-posed when there exists a sequence
 $\{\unicode[STIX]{x1D706}_{n}\}_{n\in \mathbb{N}}$
, with
$\{\unicode[STIX]{x1D706}_{n}\}_{n\in \mathbb{N}}$
, with
 $\unicode[STIX]{x1D706}_{n}\in \boldsymbol{S}_{\unicode[STIX]{x1D706}}$
for all
$\unicode[STIX]{x1D706}_{n}\in \boldsymbol{S}_{\unicode[STIX]{x1D706}}$
for all
 $n\in \mathbb{N}$
, and such that
$n\in \mathbb{N}$
, and such that
 $\text{Re}(\unicode[STIX]{x1D706}_{n})\rightarrow -\infty$
as
$\text{Re}(\unicode[STIX]{x1D706}_{n})\rightarrow -\infty$
as
 $n\rightarrow \infty$
.
$n\rightarrow \infty$
.
It now follows directly from (3.71) and (3.72) that the linear evolution problem (3.45)–(3.52) is:
-
(i) well-posed and stable when
 $\unicode[STIX]{x1D707}>0$
;
$\unicode[STIX]{x1D707}>0$
; -
(ii) ill-posed when
 $\unicode[STIX]{x1D707}<0$
.
$\unicode[STIX]{x1D707}<0$
.
We conclude that [IBVP] is well-posed and stable when
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,\unicode[STIX]{x03C0}/2)\times \mathbb{R}^{+}$
, whilst [IBVP] is ill-posed when
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,\unicode[STIX]{x03C0}/2)\times \mathbb{R}^{+}$
, whilst [IBVP] is ill-posed when
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,\unicode[STIX]{x03C0}/2)\times \mathbb{R}^{-}$
. We should note here that the time scale for ill-posed growth or stable decay for the perturbation close to the initial contact point corresponds to
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,\unicode[STIX]{x03C0}/2)\times \mathbb{R}^{-}$
. We should note here that the time scale for ill-posed growth or stable decay for the perturbation close to the initial contact point corresponds to
![]() $\unicode[STIX]{x1D70F}\gg 1$
, which in the original time variable has
$\unicode[STIX]{x1D70F}\gg 1$
, which in the original time variable has
![]() $t\gg O(\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x1D6FC}/\unicode[STIX]{x03C0}})$
.
$t\gg O(\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x1D6FC}/\unicode[STIX]{x03C0}})$
.
We next consider the problem (3.45)–(3.52) in the case
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,\unicode[STIX]{x03C0}/4]\times \{0\}$
, where it is straightforward to show that the only solution is given by
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,\unicode[STIX]{x03C0}/4]\times \{0\}$
, where it is straightforward to show that the only solution is given by
and thus the linear evolution problem (3.45)–(3.52) is well-posed and stable for all pairs
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,\unicode[STIX]{x03C0}/4]\times \{0\}$
. We conclude that [IBVP] is well-posed and stable when
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,\unicode[STIX]{x03C0}/4]\times \{0\}$
. We conclude that [IBVP] is well-posed and stable when
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,\unicode[STIX]{x03C0}/4]\times \{0\}$
.
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,\unicode[STIX]{x03C0}/4]\times \{0\}$
.
It remains to consider the well-posedness and stability of [IBVP] for those pairs
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (\unicode[STIX]{x03C0}/4,\unicode[STIX]{x03C0}/2)\times {\mathcal{G}}(\unicode[STIX]{x1D6FF})$
, with
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (\unicode[STIX]{x03C0}/4,\unicode[STIX]{x03C0}/2)\times {\mathcal{G}}(\unicode[STIX]{x1D6FF})$
, with
![]() ${\mathcal{G}}(\unicode[STIX]{x1D6FF})$
being an
${\mathcal{G}}(\unicode[STIX]{x1D6FF})$
being an
![]() $o(1)$
neighbourhood of
$o(1)$
neighbourhood of
![]() $\unicode[STIX]{x1D707}=0$
as
$\unicode[STIX]{x1D707}=0$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
.
$\unicode[STIX]{x1D6FF}\rightarrow 0$
.
4 The case
 $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (\unicode[STIX]{x03C0}/4,\unicode[STIX]{x03C0}/2)\times {\mathcal{G}}(\unicode[STIX]{x1D6FF})$
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (\unicode[STIX]{x03C0}/4,\unicode[STIX]{x03C0}/2)\times {\mathcal{G}}(\unicode[STIX]{x1D6FF})$
We now investigate the well-posedness and stability of the problem [IBVP] with respect to perturbations in the initial data for those pairs
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (\unicode[STIX]{x03C0}/4,\unicode[STIX]{x03C0}/2)\times {\mathcal{G}}(\unicode[STIX]{x1D6FF})$
, with
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (\unicode[STIX]{x03C0}/4,\unicode[STIX]{x03C0}/2)\times {\mathcal{G}}(\unicode[STIX]{x1D6FF})$
, with
![]() ${\mathcal{G}}(\unicode[STIX]{x1D6FF})$
being an
${\mathcal{G}}(\unicode[STIX]{x1D6FF})$
being an
![]() $o(1)$
neighbourhood of
$o(1)$
neighbourhood of
![]() $\unicode[STIX]{x1D707}=0$
as
$\unicode[STIX]{x1D707}=0$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
. We write
$\unicode[STIX]{x1D6FF}\rightarrow 0$
. We write
where
![]() $\overline{\unicode[STIX]{x1D707}}=O(1)$
and
$\overline{\unicode[STIX]{x1D707}}=O(1)$
and
![]() $\unicode[STIX]{x1D700}(\unicode[STIX]{x1D6FF})=o(1)$
as
$\unicode[STIX]{x1D700}(\unicode[STIX]{x1D6FF})=o(1)$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
. Here the gauge function
$\unicode[STIX]{x1D6FF}\rightarrow 0$
. Here the gauge function
![]() $\unicode[STIX]{x1D700}(\unicode[STIX]{x1D6FF})$
will be determined in the course of the analysis. Following an examination of the inner–inner region asymptotic expansions given in GNB (see (5.2) and (5.3)), we require
$\unicode[STIX]{x1D700}(\unicode[STIX]{x1D6FF})$
will be determined in the course of the analysis. Following an examination of the inner–inner region asymptotic expansions given in GNB (see (5.2) and (5.3)), we require
![]() $t^{\unicode[STIX]{x1D6FE}}\sim \unicode[STIX]{x1D6FF}$
and
$t^{\unicode[STIX]{x1D6FE}}\sim \unicode[STIX]{x1D6FF}$
and
![]() $t^{\unicode[STIX]{x1D6FE}}\sim \unicode[STIX]{x1D6FF}^{m}$
, which, as
$t^{\unicode[STIX]{x1D6FE}}\sim \unicode[STIX]{x1D6FF}^{m}$
, which, as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
, requires
$\unicode[STIX]{x1D6FF}\rightarrow 0$
, requires
where
![]() $\unicode[STIX]{x1D6FE}=1/(1-\unicode[STIX]{x03C0}/4\unicode[STIX]{x1D6FC})$
. Hereafter we will refer to the initially perturbed modification of [IBVP] as
$\unicode[STIX]{x1D6FE}=1/(1-\unicode[STIX]{x03C0}/4\unicode[STIX]{x1D6FC})$
. Hereafter we will refer to the initially perturbed modification of [IBVP] as
![]() $\text{[IBVP]}^{\prime \prime }$
, and we will address
$\text{[IBVP]}^{\prime \prime }$
, and we will address
![]() $\text{[IBVP]}^{\prime \prime }$
as
$\text{[IBVP]}^{\prime \prime }$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
with
$\unicode[STIX]{x1D6FF}\rightarrow 0$
with
![]() $t=O(\unicode[STIX]{x1D6FF}^{1/\unicode[STIX]{x1D6FE}})$
. Thus we write
$t=O(\unicode[STIX]{x1D6FF}^{1/\unicode[STIX]{x1D6FE}})$
. Thus we write
where
![]() $\unicode[STIX]{x1D70F}=O(1)$
as
$\unicode[STIX]{x1D70F}=O(1)$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
. We can now write
$\unicode[STIX]{x1D6FF}\rightarrow 0$
. We can now write
![]() $\text{[IBVP]}^{\prime \prime }$
in terms of
$\text{[IBVP]}^{\prime \prime }$
in terms of
![]() $\overline{x}$
,
$\overline{x}$
,
![]() $y$
,
$y$
,
![]() $\unicode[STIX]{x1D719}$
,
$\unicode[STIX]{x1D719}$
,
![]() $\unicode[STIX]{x1D702}$
,
$\unicode[STIX]{x1D702}$
,
![]() $\unicode[STIX]{x1D70F}$
and
$\unicode[STIX]{x1D70F}$
and
![]() $\unicode[STIX]{x1D6FF}$
, which becomes
$\unicode[STIX]{x1D6FF}$
, which becomes
The structure of the solution to [IBVP] as
![]() $t\rightarrow 0^{+}$
(see GNB) indicates that there will be three asymptotic regions in the solution to
$t\rightarrow 0^{+}$
(see GNB) indicates that there will be three asymptotic regions in the solution to
![]() $\text{[IBVP]}^{\prime \prime }$
as
$\text{[IBVP]}^{\prime \prime }$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
when
$\unicode[STIX]{x1D6FF}\rightarrow 0$
when
![]() $\unicode[STIX]{x1D70F}=O(1)$
. In the outer region we have
$\unicode[STIX]{x1D70F}=O(1)$
. In the outer region we have
![]() $(\overline{x},y)\in \overline{{\mathcal{D}}}(\unicode[STIX]{x1D70F})=O(1)$
as
$(\overline{x},y)\in \overline{{\mathcal{D}}}(\unicode[STIX]{x1D70F})=O(1)$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
when
$\unicode[STIX]{x1D6FF}\rightarrow 0$
when
![]() $\unicode[STIX]{x1D70F}=O(1)$
, and we consider this first.
$\unicode[STIX]{x1D70F}=O(1)$
, and we consider this first.
4.1 Outer region for
 $\text{[IBVP]}^{\prime \prime }$
when
$\text{[IBVP]}^{\prime \prime }$
when
 $\unicode[STIX]{x1D70F}=O(1)$
as
$\unicode[STIX]{x1D70F}=O(1)$
as
 $\unicode[STIX]{x1D6FF}\rightarrow 0$
$\unicode[STIX]{x1D6FF}\rightarrow 0$
We begin in an outer region in which
![]() $(\overline{x},y)\in \overline{{\mathcal{D}}}(\unicode[STIX]{x1D70F})=O(1)$
, when
$(\overline{x},y)\in \overline{{\mathcal{D}}}(\unicode[STIX]{x1D70F})=O(1)$
, when
![]() $\unicode[STIX]{x1D70F}=O(1)$
as
$\unicode[STIX]{x1D70F}=O(1)$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
, after which we will require two additional regions, in which
$\unicode[STIX]{x1D6FF}\rightarrow 0$
, after which we will require two additional regions, in which
![]() $(\overline{x},y)=o(1)$
as
$(\overline{x},y)=o(1)$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
, in order to capture the initial interaction between the plate and the free surface. We observe that conditions (4.5) and (4.7) require
$\unicode[STIX]{x1D6FF}\rightarrow 0$
, in order to capture the initial interaction between the plate and the free surface. We observe that conditions (4.5) and (4.7) require
![]() $\unicode[STIX]{x1D719}=O(\unicode[STIX]{x1D6FF}^{1/\unicode[STIX]{x1D6FE}})$
and
$\unicode[STIX]{x1D719}=O(\unicode[STIX]{x1D6FF}^{1/\unicode[STIX]{x1D6FE}})$
and
![]() $\unicode[STIX]{x1D702}=O(\unicode[STIX]{x1D6FF}^{2/\unicode[STIX]{x1D6FE}})$
as
$\unicode[STIX]{x1D702}=O(\unicode[STIX]{x1D6FF}^{2/\unicode[STIX]{x1D6FE}})$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
in the outer region. Thus we introduce the asymptotic expansions
$\unicode[STIX]{x1D6FF}\rightarrow 0$
in the outer region. Thus we introduce the asymptotic expansions
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
in the outer region, with the factor
$\unicode[STIX]{x1D6FF}\rightarrow 0$
in the outer region, with the factor
![]() $-\cos \,\unicode[STIX]{x1D6FC}$
in (4.14) included for algebraic convenience at a later stage. Substituting the expansions (4.14) and (4.15) into
$-\cos \,\unicode[STIX]{x1D6FC}$
in (4.14) included for algebraic convenience at a later stage. Substituting the expansions (4.14) and (4.15) into
![]() $\text{[IBVP]}^{\prime \prime }$
we obtain, at leading order, a problem equivalent to (3.15)–(3.22) in the case
$\text{[IBVP]}^{\prime \prime }$
we obtain, at leading order, a problem equivalent to (3.15)–(3.22) in the case
![]() $\unicode[STIX]{x1D707}=0$
. It follows that, after writing
$\unicode[STIX]{x1D707}=0$
. It follows that, after writing
then
![]() $\overline{\unicode[STIX]{x1D719}}^{\prime \prime }$
and
$\overline{\unicode[STIX]{x1D719}}^{\prime \prime }$
and
![]() $\overline{\unicode[STIX]{x1D702}}^{\prime \prime }$
are given (for some real constants
$\overline{\unicode[STIX]{x1D702}}^{\prime \prime }$
are given (for some real constants
![]() $A_{n}$
,
$A_{n}$
,
![]() $B_{n}$
and
$B_{n}$
and
![]() $C_{n}$
) by (3.24)–(3.28). The form of
$C_{n}$
) by (3.24)–(3.28). The form of
![]() $\overline{\unicode[STIX]{x1D719}}^{\prime \prime }$
and
$\overline{\unicode[STIX]{x1D719}}^{\prime \prime }$
and
![]() $\overline{\unicode[STIX]{x1D702}}^{\prime \prime }$
as
$\overline{\unicode[STIX]{x1D702}}^{\prime \prime }$
as
![]() $(\overline{x},y)\rightarrow (0,0)$
is given by (3.29) and (3.30), where we again have singular behaviour as
$(\overline{x},y)\rightarrow (0,0)$
is given by (3.29) and (3.30), where we again have singular behaviour as
![]() $(\overline{x},y)\rightarrow (0,0)$
, which motivates the introduction of an inner region in which
$(\overline{x},y)\rightarrow (0,0)$
, which motivates the introduction of an inner region in which
![]() $(\overline{x},y)=o(1)$
as
$(\overline{x},y)=o(1)$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
.
$\unicode[STIX]{x1D6FF}\rightarrow 0$
.
4.2 Inner region for
 $\text{[IBVP]}^{\prime \prime }$
when
$\text{[IBVP]}^{\prime \prime }$
when
 $\unicode[STIX]{x1D70F}=O(1)$
as
$\unicode[STIX]{x1D70F}=O(1)$
as
 $\unicode[STIX]{x1D6FF}\rightarrow 0$
$\unicode[STIX]{x1D6FF}\rightarrow 0$
We set
![]() $(\overline{x},y)=O(\overline{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D6FF}))$
with
$(\overline{x},y)=O(\overline{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D6FF}))$
with
![]() $\overline{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D6FF})=o(1)$
as
$\overline{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D6FF})=o(1)$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
in the inner region. It follows from (4.15), and (4.16), along with (3.23) and (3.30), that
$\unicode[STIX]{x1D6FF}\rightarrow 0$
in the inner region. It follows from (4.15), and (4.16), along with (3.23) and (3.30), that
![]() $\unicode[STIX]{x1D702}=O(\unicode[STIX]{x1D6FF}^{2/\unicode[STIX]{x1D6FE}})$
as
$\unicode[STIX]{x1D702}=O(\unicode[STIX]{x1D6FF}^{2/\unicode[STIX]{x1D6FE}})$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
in the inner region, and so, in order to capture the free surface in the inner region, we must take
$\unicode[STIX]{x1D6FF}\rightarrow 0$
in the inner region, and so, in order to capture the free surface in the inner region, we must take
![]() $\overline{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D6FF})=O(\unicode[STIX]{x1D6FF}^{2/\unicode[STIX]{x1D6FE}})$
as
$\overline{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D6FF})=O(\unicode[STIX]{x1D6FF}^{2/\unicode[STIX]{x1D6FE}})$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
; thus without loss of generality, we set
$\unicode[STIX]{x1D6FF}\rightarrow 0$
; thus without loss of generality, we set
![]() $\overline{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D6FF})=\unicode[STIX]{x1D6FF}^{2/\unicode[STIX]{x1D6FE}}$
. An examination of (4.14), together with (3.23) and (3.29), then requires that
$\overline{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D6FF})=\unicode[STIX]{x1D6FF}^{2/\unicode[STIX]{x1D6FE}}$
. An examination of (4.14), together with (3.23) and (3.29), then requires that
![]() $\unicode[STIX]{x1D719}=O(\unicode[STIX]{x1D6FF}^{3/\unicode[STIX]{x1D6FE}})$
as
$\unicode[STIX]{x1D719}=O(\unicode[STIX]{x1D6FF}^{3/\unicode[STIX]{x1D6FE}})$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
in the inner region. Thus we introduce scaled inner region coordinates
$\unicode[STIX]{x1D6FF}\rightarrow 0$
in the inner region. Thus we introduce scaled inner region coordinates
![]() $(X,Y)$
by
$(X,Y)$
by
with
![]() $(X,Y)=O(1)$
as
$(X,Y)=O(1)$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
in the inner region (
$\unicode[STIX]{x1D6FF}\rightarrow 0$
in the inner region (
![]() $\dagger$
). The location of the plate in the inner region is given by
$\dagger$
). The location of the plate in the inner region is given by
![]() $Y=-X\tan \unicode[STIX]{x1D6FC}$
, whilst the contact point is denoted by
$Y=-X\tan \unicode[STIX]{x1D6FC}$
, whilst the contact point is denoted by
![]() $(X,Y)=(X_{p}(\unicode[STIX]{x1D70F}),Y_{p}(\unicode[STIX]{x1D70F}))$
, where
$(X,Y)=(X_{p}(\unicode[STIX]{x1D70F}),Y_{p}(\unicode[STIX]{x1D70F}))$
, where
![]() $\overline{x}_{p}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D6FF}^{2/\unicode[STIX]{x1D6FE}}X_{p}(\unicode[STIX]{x1D70F})$
and
$\overline{x}_{p}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D6FF}^{2/\unicode[STIX]{x1D6FE}}X_{p}(\unicode[STIX]{x1D70F})$
and
![]() $y_{p}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D6FF}^{2/\unicode[STIX]{x1D6FE}}Y_{p}(\unicode[STIX]{x1D70F})$
(
$y_{p}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D6FF}^{2/\unicode[STIX]{x1D6FE}}Y_{p}(\unicode[STIX]{x1D70F})$
(
![]() $\dagger$
). We now write the free surface and velocity potential in the inner region as
$\dagger$
). We now write the free surface and velocity potential in the inner region as
where
![]() $\unicode[STIX]{x1D702}_{I}(X,\unicode[STIX]{x1D70F})$
,
$\unicode[STIX]{x1D702}_{I}(X,\unicode[STIX]{x1D70F})$
,
![]() $\unicode[STIX]{x1D719}_{I}(X,Y,\unicode[STIX]{x1D70F})=O(1)$
as
$\unicode[STIX]{x1D719}_{I}(X,Y,\unicode[STIX]{x1D70F})=O(1)$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
(
$\unicode[STIX]{x1D6FF}\rightarrow 0$
(
![]() $\dagger$
). The inner region expansions are then introduced as
$\dagger$
). The inner region expansions are then introduced as
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
where
$\unicode[STIX]{x1D6FF}\rightarrow 0$
where
![]() $(X,Y)=O(1)$
, with the form of the correction terms having been deduced from (4.17), together with (3.14), (3.23) and (3.30). It also follows from (4.17) and (4.20) that the free surface in the inner region is located at
$(X,Y)=O(1)$
, with the form of the correction terms having been deduced from (4.17), together with (3.14), (3.23) and (3.30). It also follows from (4.17) and (4.20) that the free surface in the inner region is located at
and hence we must expand
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
, after which
$\unicode[STIX]{x1D6FF}\rightarrow 0$
, after which
![]() $Y_{p}(\unicode[STIX]{x1D70F})=-X_{p}(\unicode[STIX]{x1D70F})\tan \unicode[STIX]{x1D6FC}$
(
$Y_{p}(\unicode[STIX]{x1D70F})=-X_{p}(\unicode[STIX]{x1D70F})\tan \unicode[STIX]{x1D6FC}$
(
![]() $\dagger$
).
$\dagger$
).
We can now write
![]() $\text{[IBVP]}^{\prime \prime }$
in terms of the inner variables and substitute from (4.20) and (4.21). The problem obtained at leading order, when supplemented with matching conditions to the outer region (via Van Dyke’s matching principle, (Van Dyke Reference Van Dyke1964)), has the solution
$\text{[IBVP]}^{\prime \prime }$
in terms of the inner variables and substitute from (4.20) and (4.21). The problem obtained at leading order, when supplemented with matching conditions to the outer region (via Van Dyke’s matching principle, (Van Dyke Reference Van Dyke1964)), has the solution
It follows from (4.24) and (4.25), using (4.17)–(4.21), that the regularity conditions (see GNB (2.16)) are satisfied at leading order in the inner region. We now formulate the problem at
![]() $O(\unicode[STIX]{x1D6FF}^{(\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2)/\unicode[STIX]{x1D6FE}})$
, where it is convenient to introduce the coordinates
$O(\unicode[STIX]{x1D6FF}^{(\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2)/\unicode[STIX]{x1D6FE}})$
, where it is convenient to introduce the coordinates
![]() $(\overline{X},\overline{Y})$
according to
$(\overline{X},\overline{Y})$
according to
which is simply a shift of origin from the original inner region coordinates
![]() $(X,Y)$
(
$(X,Y)$
(
![]() $\dagger$
). We now obtain the problem for
$\dagger$
). We now obtain the problem for
![]() $\widetilde{\unicode[STIX]{x1D719}}_{1}^{\prime \prime }$
,
$\widetilde{\unicode[STIX]{x1D719}}_{1}^{\prime \prime }$
,
![]() $\widetilde{\unicode[STIX]{x1D702}}_{1}^{\prime \prime }$
and
$\widetilde{\unicode[STIX]{x1D702}}_{1}^{\prime \prime }$
and
![]() $X_{1}$
, as
$X_{1}$
, as
 $$\begin{eqnarray}\displaystyle & & \displaystyle \widetilde{\unicode[STIX]{x1D719}}_{1}^{\prime \prime }(\overline{R},\unicode[STIX]{x1D703})=\unicode[STIX]{x1D70F}A_{0}(\unicode[STIX]{x1D6FC})\cos \unicode[STIX]{x1D6FC}\overline{R}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}}\cos \frac{\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D703}+\unicode[STIX]{x1D6FC})+o(\overline{R}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}})\nonumber\\ \displaystyle & & \displaystyle \quad \text{as }\overline{R}\rightarrow \infty ,-\unicode[STIX]{x1D6FC}<\unicode[STIX]{x1D703}<0,\unicode[STIX]{x1D70F}>0;\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \widetilde{\unicode[STIX]{x1D719}}_{1}^{\prime \prime }(\overline{R},\unicode[STIX]{x1D703})=\unicode[STIX]{x1D70F}A_{0}(\unicode[STIX]{x1D6FC})\cos \unicode[STIX]{x1D6FC}\overline{R}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}}\cos \frac{\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D703}+\unicode[STIX]{x1D6FC})+o(\overline{R}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}})\nonumber\\ \displaystyle & & \displaystyle \quad \text{as }\overline{R}\rightarrow \infty ,-\unicode[STIX]{x1D6FC}<\unicode[STIX]{x1D703}<0,\unicode[STIX]{x1D70F}>0;\end{eqnarray}$$
Here
![]() $\overline{\unicode[STIX]{x1D735}}=(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\overline{X},\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\overline{Y})$
, (4.32) and (4.33) are the matching conditions with the outer region,
$\overline{\unicode[STIX]{x1D735}}=(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\overline{X},\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\overline{Y})$
, (4.32) and (4.33) are the matching conditions with the outer region,
![]() $A_{0}(\unicode[STIX]{x1D6FC})({<}\!0)$
is given in GNB (see (3.10)), and we have introduced polar coordinates
$A_{0}(\unicode[STIX]{x1D6FC})({<}\!0)$
is given in GNB (see (3.10)), and we have introduced polar coordinates
![]() $(\overline{R},\unicode[STIX]{x1D703})$
, given by
$(\overline{R},\unicode[STIX]{x1D703})$
, given by
![]() $\overline{X}=\overline{R}\cos \unicode[STIX]{x1D703}$
,
$\overline{X}=\overline{R}\cos \unicode[STIX]{x1D703}$
,
![]() $\overline{Y}=\overline{R}\sin \unicode[STIX]{x1D703}$
(
$\overline{Y}=\overline{R}\sin \unicode[STIX]{x1D703}$
(
![]() $\dagger$
). Additionally we have
$\dagger$
). Additionally we have
It is straightforward to show that, in this degenerate case, the solution to the problem (4.28)–(4.35), which has least singular behaviour at
![]() $(\overline{X},\overline{Y})=(0,0)$
is simply given exactly by the far-field functions, that is
$(\overline{X},\overline{Y})=(0,0)$
is simply given exactly by the far-field functions, that is
 $$\begin{eqnarray}\displaystyle \widetilde{\unicode[STIX]{x1D719}}_{1}^{\prime \prime }(\overline{R},\unicode[STIX]{x1D703},\unicode[STIX]{x1D70F}) & = & \displaystyle \unicode[STIX]{x1D70F}A_{0}(\unicode[STIX]{x1D6FC})\cos \unicode[STIX]{x1D6FC}\overline{R}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}}\cos \frac{\unicode[STIX]{x03C0}}{2\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D703}+\unicode[STIX]{x1D6FC}),\nonumber\\ \displaystyle & & \displaystyle \quad \overline{R}>0,-\unicode[STIX]{x1D6FC}<\unicode[STIX]{x1D703}<0,\unicode[STIX]{x1D70F}>0;\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widetilde{\unicode[STIX]{x1D719}}_{1}^{\prime \prime }(\overline{R},\unicode[STIX]{x1D703},\unicode[STIX]{x1D70F}) & = & \displaystyle \unicode[STIX]{x1D70F}A_{0}(\unicode[STIX]{x1D6FC})\cos \unicode[STIX]{x1D6FC}\overline{R}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}}\cos \frac{\unicode[STIX]{x03C0}}{2\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D703}+\unicode[STIX]{x1D6FC}),\nonumber\\ \displaystyle & & \displaystyle \quad \overline{R}>0,-\unicode[STIX]{x1D6FC}<\unicode[STIX]{x1D703}<0,\unicode[STIX]{x1D70F}>0;\end{eqnarray}$$
We see from (4.37) and (4.38) that a weak singularity in derivatives (that is
![]() $\widetilde{\unicode[STIX]{x1D702}}_{1,\overline{X}}^{\prime \prime }$
, and
$\widetilde{\unicode[STIX]{x1D702}}_{1,\overline{X}}^{\prime \prime }$
, and
![]() $\overline{\unicode[STIX]{x1D735}}\widetilde{\unicode[STIX]{x1D719}}_{1}^{\prime \prime }$
) persists close to the contact point and, in particular, when
$\overline{\unicode[STIX]{x1D735}}\widetilde{\unicode[STIX]{x1D719}}_{1}^{\prime \prime }$
) persists close to the contact point and, in particular, when
![]() $(\overline{X},\overline{Y})=O(\unicode[STIX]{x1D6FF}^{(\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2)/\unicode[STIX]{x1D6FE}})$
. This requires the introduction of an inner–inner region, in which
$(\overline{X},\overline{Y})=O(\unicode[STIX]{x1D6FF}^{(\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2)/\unicode[STIX]{x1D6FE}})$
. This requires the introduction of an inner–inner region, in which
![]() $(\overline{X},\overline{Y})=o(1)$
as
$(\overline{X},\overline{Y})=o(1)$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
and within which the full regularity conditions at the contact point are satisfied.
$\unicode[STIX]{x1D6FF}\rightarrow 0$
and within which the full regularity conditions at the contact point are satisfied.
4.3 Inner–inner region for
 $\text{[IBVP]}^{\prime \prime }$
when
$\text{[IBVP]}^{\prime \prime }$
when
 $\unicode[STIX]{x1D70F}=O(1)$
as
$\unicode[STIX]{x1D70F}=O(1)$
as
 $\unicode[STIX]{x1D6FF}\rightarrow 0$
$\unicode[STIX]{x1D6FF}\rightarrow 0$
We set
![]() $(\overline{X},\overline{Y})=O(\unicode[STIX]{x0394}(\unicode[STIX]{x1D6FF}))$
, with
$(\overline{X},\overline{Y})=O(\unicode[STIX]{x0394}(\unicode[STIX]{x1D6FF}))$
, with
![]() $\unicode[STIX]{x0394}(\unicode[STIX]{x1D6FF})=O(1)$
as
$\unicode[STIX]{x0394}(\unicode[STIX]{x1D6FF})=O(1)$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
. It then follows from (4.20), (4.25) and (4.38) that the free surface is located at
$\unicode[STIX]{x1D6FF}\rightarrow 0$
. It then follows from (4.20), (4.25) and (4.38) that the free surface is located at
![]() $\overline{Y}=\unicode[STIX]{x1D70F}^{2}/2+\unicode[STIX]{x1D702}_{I}=O(\unicode[STIX]{x1D6FF}^{(\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2)/\unicode[STIX]{x1D6FE}}\unicode[STIX]{x0394}(\unicode[STIX]{x1D6FF})^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-1})$
as
$\overline{Y}=\unicode[STIX]{x1D70F}^{2}/2+\unicode[STIX]{x1D702}_{I}=O(\unicode[STIX]{x1D6FF}^{(\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2)/\unicode[STIX]{x1D6FE}}\unicode[STIX]{x0394}(\unicode[STIX]{x1D6FF})^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-1})$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
in the inner–inner region. Therefore, to capture the free surface in the inner–inner region, we must take
$\unicode[STIX]{x1D6FF}\rightarrow 0$
in the inner–inner region. Therefore, to capture the free surface in the inner–inner region, we must take
![]() $\unicode[STIX]{x0394}(\unicode[STIX]{x1D6FF})=O(\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-1})$
, and so, without loss of generality, we set
$\unicode[STIX]{x0394}(\unicode[STIX]{x1D6FF})=O(\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-1})$
, and so, without loss of generality, we set
![]() $\unicode[STIX]{x0394}(\unicode[STIX]{x1D6FF})=\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-1}$
. We introduce scaled inner–inner region coordinates
$\unicode[STIX]{x0394}(\unicode[STIX]{x1D6FF})=\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-1}$
. We introduce scaled inner–inner region coordinates
![]() $(\widetilde{x},\widetilde{y})$
by
$(\widetilde{x},\widetilde{y})$
by
where
![]() $(\widetilde{x},\widetilde{y})=O(1)$
as
$(\widetilde{x},\widetilde{y})=O(1)$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
in the inner–inner region (
$\unicode[STIX]{x1D6FF}\rightarrow 0$
in the inner–inner region (
![]() $\dagger$
). The location of the plate in the inner–inner region is given by
$\dagger$
). The location of the plate in the inner–inner region is given by
![]() $\widetilde{y}=-\widetilde{x}\tan \unicode[STIX]{x1D6FC}$
, with the plate and contact point denoted by
$\widetilde{y}=-\widetilde{x}\tan \unicode[STIX]{x1D6FC}$
, with the plate and contact point denoted by
![]() $(\widetilde{x},\widetilde{y})=(\widetilde{x}_{p}(\unicode[STIX]{x1D70F}),\widetilde{y}_{p}(\unicode[STIX]{x1D70F}))$
, with
$(\widetilde{x},\widetilde{y})=(\widetilde{x}_{p}(\unicode[STIX]{x1D70F}),\widetilde{y}_{p}(\unicode[STIX]{x1D70F}))$
, with
![]() $\widetilde{x}_{p}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-1}\overline{X}_{p}(\unicode[STIX]{x1D70F})$
and
$\widetilde{x}_{p}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-1}\overline{X}_{p}(\unicode[STIX]{x1D70F})$
and
![]() $\widetilde{y}_{p}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-1}\overline{Y}_{p}(\unicode[STIX]{x1D70F})$
(
$\widetilde{y}_{p}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-1}\overline{Y}_{p}(\unicode[STIX]{x1D70F})$
(
![]() $\dagger$
), where
$\dagger$
), where
An examination of (4.20), (4.21), (4.24), (4.25), (4.37) and (4.38) requires that
![]() $\unicode[STIX]{x1D702}_{I}=-\unicode[STIX]{x1D70F}^{2}/2+O(\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-1})$
and
$\unicode[STIX]{x1D702}_{I}=-\unicode[STIX]{x1D70F}^{2}/2+O(\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-1})$
and
![]() $\unicode[STIX]{x1D719}_{I}=\unicode[STIX]{x1D70F}^{3}/3-\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-1}\unicode[STIX]{x1D70F}\widetilde{y}+O(\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2})$
as
$\unicode[STIX]{x1D719}_{I}=\unicode[STIX]{x1D70F}^{3}/3-\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-1}\unicode[STIX]{x1D70F}\widetilde{y}+O(\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2})$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
. We thus write the free surface and velocity potential in the inner–inner region as
$\unicode[STIX]{x1D6FF}\rightarrow 0$
. We thus write the free surface and velocity potential in the inner–inner region as
where
![]() $\unicode[STIX]{x1D702}_{II}$
,
$\unicode[STIX]{x1D702}_{II}$
,
![]() $\unicode[STIX]{x1D719}_{II}=O(1)$
as
$\unicode[STIX]{x1D719}_{II}=O(1)$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
(
$\unicode[STIX]{x1D6FF}\rightarrow 0$
(
![]() $\dagger$
). The inner–inner region asymptotic expansions are then introduced as
$\dagger$
). The inner–inner region asymptotic expansions are then introduced as
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
, where
$\unicode[STIX]{x1D6FF}\rightarrow 0$
, where
![]() $(\widetilde{x},\widetilde{y})=O(1)$
. It follows from (4.39) and (4.43) that the free surface in the inner–inner region is located at
$(\widetilde{x},\widetilde{y})=O(1)$
. It follows from (4.39) and (4.43) that the free surface in the inner–inner region is located at
and hence we must expand
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
, after which
$\unicode[STIX]{x1D6FF}\rightarrow 0$
, after which
![]() $\widetilde{y}_{p}(\unicode[STIX]{x1D70F})=-\widetilde{x}_{p}(\unicode[STIX]{x1D70F})\tan \unicode[STIX]{x1D6FC}$
(
$\widetilde{y}_{p}(\unicode[STIX]{x1D70F})=-\widetilde{x}_{p}(\unicode[STIX]{x1D70F})\tan \unicode[STIX]{x1D6FC}$
(
![]() $\dagger$
). An examination of the plate boundary condition (4.5), (4.39) and (4.42), together with (4.1), then requires that the gauge function
$\dagger$
). An examination of the plate boundary condition (4.5), (4.39) and (4.42), together with (4.1), then requires that the gauge function
![]() $\unicode[STIX]{x1D700}(\unicode[STIX]{x1D6FF})=O(\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-1})$
(from which it follows that
$\unicode[STIX]{x1D700}(\unicode[STIX]{x1D6FF})=O(\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-1})$
(from which it follows that
![]() ${\mathcal{G}}(\unicode[STIX]{x1D700})=O(\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-1})$
), and so, without loss of generality, we set
${\mathcal{G}}(\unicode[STIX]{x1D700})=O(\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-1})$
), and so, without loss of generality, we set
![]() $\unicode[STIX]{x1D700}(\unicode[STIX]{x1D6FF})=\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-1}$
. We are now able to write
$\unicode[STIX]{x1D700}(\unicode[STIX]{x1D6FF})=\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-1}$
. We are now able to write
![]() $\text{[IBVP]}^{\prime \prime }$
in terms of the inner–inner region variables and substitute from (4.43). It is convenient to first introduce the dependent variables
$\text{[IBVP]}^{\prime \prime }$
in terms of the inner–inner region variables and substitute from (4.43). It is convenient to first introduce the dependent variables
![]() $\unicode[STIX]{x1D6F7}^{\prime \prime }$
and
$\unicode[STIX]{x1D6F7}^{\prime \prime }$
and
![]() $H^{\prime \prime }$
, according to
$H^{\prime \prime }$
, according to
along with the translated coordinates
![]() $(\widehat{x},\widehat{y})$
, according to
$(\widehat{x},\widehat{y})$
, according to
which is simply a shift of origin from the original inner–inner coordinates
![]() $(\widetilde{x},\widetilde{y})$
(
$(\widetilde{x},\widetilde{y})$
(
![]() $\dagger$
). The variable changes (4.46) and (4.47) have been chosen for algebraic convenience at a later stage. We obtain at leading order the following nonlinear harmonic evolution free boundary problem for
$\dagger$
). The variable changes (4.46) and (4.47) have been chosen for algebraic convenience at a later stage. We obtain at leading order the following nonlinear harmonic evolution free boundary problem for
![]() $\unicode[STIX]{x1D6F7}^{\prime \prime }$
,
$\unicode[STIX]{x1D6F7}^{\prime \prime }$
,
![]() $H^{\prime \prime }$
and
$H^{\prime \prime }$
and
![]() $\widehat{x}_{0}$
, namely
$\widehat{x}_{0}$
, namely
where
Here
![]() $\widehat{\unicode[STIX]{x1D735}}=(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\widehat{x},\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\widehat{y})$
,
$\widehat{\unicode[STIX]{x1D735}}=(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\widehat{x},\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\widehat{y})$
,
![]() $A_{0}(\unicode[STIX]{x1D6FC})({<}0)$
is as given in GNB (see (3.10)), and we have introduced polar coordinates
$A_{0}(\unicode[STIX]{x1D6FC})({<}0)$
is as given in GNB (see (3.10)), and we have introduced polar coordinates
![]() $(\widehat{r},\unicode[STIX]{x1D703})$
as
$(\widehat{r},\unicode[STIX]{x1D703})$
as
![]() $\widehat{x}=\widehat{r}\cos \unicode[STIX]{x1D703}$
,
$\widehat{x}=\widehat{r}\cos \unicode[STIX]{x1D703}$
,
![]() $\widehat{y}=\widehat{r}\sin \unicode[STIX]{x1D703}$
(
$\widehat{y}=\widehat{r}\sin \unicode[STIX]{x1D703}$
(
![]() $\dagger$
). The initial boundary value problem (4.48)–(4.56), henceforth referred to as [EBVP], can now be solved numerically using a boundary integral method, which follows the approach discussed in GNB, with implicit time stepping to evolve the solution in time
$\dagger$
). The initial boundary value problem (4.48)–(4.56), henceforth referred to as [EBVP], can now be solved numerically using a boundary integral method, which follows the approach discussed in GNB, with implicit time stepping to evolve the solution in time
![]() $\unicode[STIX]{x1D70F}$
.
$\unicode[STIX]{x1D70F}$
.
Figure 2. Graph of the evolution of
![]() $H^{\prime \prime }(\widehat{x},\unicode[STIX]{x1D70F})$
(related to the free surface displacement through (4.46), (4.43), (4.41) and (4.18)) against
$H^{\prime \prime }(\widehat{x},\unicode[STIX]{x1D70F})$
(related to the free surface displacement through (4.46), (4.43), (4.41) and (4.18)) against
![]() $\widehat{x}$
for the numerical solution of [EBVP], for
$\widehat{x}$
for the numerical solution of [EBVP], for
![]() $\unicode[STIX]{x1D70F}=0$
,
$\unicode[STIX]{x1D70F}=0$
,
![]() $\unicode[STIX]{x1D70F}=0.75$
,
$\unicode[STIX]{x1D70F}=0.75$
,
![]() $\unicode[STIX]{x1D70F}=1.5$
,
$\unicode[STIX]{x1D70F}=1.5$
,
![]() $\unicode[STIX]{x1D70F}=2.25$
,
$\unicode[STIX]{x1D70F}=2.25$
,
![]() $\unicode[STIX]{x1D70F}=3$
,
$\unicode[STIX]{x1D70F}=3$
,
![]() $\unicode[STIX]{x1D70F}=3.75$
,
$\unicode[STIX]{x1D70F}=3.75$
,
![]() $\unicode[STIX]{x1D70F}=4.5$
,
$\unicode[STIX]{x1D70F}=4.5$
,
![]() $\unicode[STIX]{x1D70F}=5.25$
and
$\unicode[STIX]{x1D70F}=5.25$
and
![]() $\unicode[STIX]{x1D70F}=6$
, (a–i) where
$\unicode[STIX]{x1D70F}=6$
, (a–i) where
![]() $\overline{\unicode[STIX]{x1D707}}=1$
and
$\overline{\unicode[STIX]{x1D707}}=1$
and
![]() $\unicode[STIX]{x1D6FC}=1.4$
. In each plot a dash-dot line shows the location of the plate, a dotted line shows the solution for the case of zero initial data and a solid line shows the solution when the initial data are as given in (4.61).
$\unicode[STIX]{x1D6FC}=1.4$
. In each plot a dash-dot line shows the location of the plate, a dotted line shows the solution for the case of zero initial data and a solid line shows the solution when the initial data are as given in (4.61).

Figure 3. Graph of the evolution of
![]() $H^{\prime \prime }(\widehat{x},\unicode[STIX]{x1D70F})$
(related to the free surface displacement through (4.46), (4.43), (4.41) and (4.18)) against
$H^{\prime \prime }(\widehat{x},\unicode[STIX]{x1D70F})$
(related to the free surface displacement through (4.46), (4.43), (4.41) and (4.18)) against
![]() $\widehat{x}$
for the numerical solution of [EBVP], for
$\widehat{x}$
for the numerical solution of [EBVP], for
![]() $\unicode[STIX]{x1D70F}=0$
,
$\unicode[STIX]{x1D70F}=0$
,
![]() $\unicode[STIX]{x1D70F}=0.13$
,
$\unicode[STIX]{x1D70F}=0.13$
,
![]() $\unicode[STIX]{x1D70F}=0.25$
,
$\unicode[STIX]{x1D70F}=0.25$
,
![]() $\unicode[STIX]{x1D70F}=0.38$
,
$\unicode[STIX]{x1D70F}=0.38$
,
![]() $\unicode[STIX]{x1D70F}=0.5$
,
$\unicode[STIX]{x1D70F}=0.5$
,
![]() $\unicode[STIX]{x1D70F}=0.63$
,
$\unicode[STIX]{x1D70F}=0.63$
,
![]() $\unicode[STIX]{x1D70F}=0.75$
,
$\unicode[STIX]{x1D70F}=0.75$
,
![]() $\unicode[STIX]{x1D70F}=0.88$
and
$\unicode[STIX]{x1D70F}=0.88$
and
![]() $\unicode[STIX]{x1D70F}=1$
, (a–i) where
$\unicode[STIX]{x1D70F}=1$
, (a–i) where
![]() $\overline{\unicode[STIX]{x1D707}}=0$
and
$\overline{\unicode[STIX]{x1D707}}=0$
and
![]() $\unicode[STIX]{x1D6FC}=1.4$
. In each plot a dash-dot line shows the location of the plate, a dotted line shows the solution for the case of zero initial data and a solid line shows the solution when the initial data are as given in (4.61).
$\unicode[STIX]{x1D6FC}=1.4$
. In each plot a dash-dot line shows the location of the plate, a dotted line shows the solution for the case of zero initial data and a solid line shows the solution when the initial data are as given in (4.61).

Figure 4. Graph of the evolution of
![]() $H^{\prime \prime }(\widehat{x},\unicode[STIX]{x1D70F})$
(related to the free surface displacement through (4.46), (4.43), (4.41) and (4.18)) against
$H^{\prime \prime }(\widehat{x},\unicode[STIX]{x1D70F})$
(related to the free surface displacement through (4.46), (4.43), (4.41) and (4.18)) against
![]() $\widehat{x}$
, showing agreement with the far-field asymptotic form (4.56) for the numerical solution of [EBVP], for
$\widehat{x}$
, showing agreement with the far-field asymptotic form (4.56) for the numerical solution of [EBVP], for
![]() $\unicode[STIX]{x1D70F}=0$
,
$\unicode[STIX]{x1D70F}=0$
,
![]() $\unicode[STIX]{x1D70F}=0.75$
,
$\unicode[STIX]{x1D70F}=0.75$
,
![]() $\unicode[STIX]{x1D70F}=1.5$
,
$\unicode[STIX]{x1D70F}=1.5$
,
![]() $\unicode[STIX]{x1D70F}=2.25$
,
$\unicode[STIX]{x1D70F}=2.25$
,
![]() $\unicode[STIX]{x1D70F}=3$
,
$\unicode[STIX]{x1D70F}=3$
,
![]() $\unicode[STIX]{x1D70F}=3.75$
,
$\unicode[STIX]{x1D70F}=3.75$
,
![]() $\unicode[STIX]{x1D70F}=4.5$
,
$\unicode[STIX]{x1D70F}=4.5$
,
![]() $\unicode[STIX]{x1D70F}=5.25$
and
$\unicode[STIX]{x1D70F}=5.25$
and
![]() $\unicode[STIX]{x1D70F}=6$
, where
$\unicode[STIX]{x1D70F}=6$
, where
![]() $\overline{\unicode[STIX]{x1D707}}=1$
, and
$\overline{\unicode[STIX]{x1D707}}=1$
, and
![]() $\unicode[STIX]{x1D6FC}=1.4$
. Here
$\unicode[STIX]{x1D6FC}=1.4$
. Here
![]() $\unicode[STIX]{x1D70F}$
increases reading from the bottom of the figure to the top. The dash-dot line shows the location of the plate, solid lines show the numerical solution when the initial data are as given in (4.61), and dotted lines plot the far-field asymptotic form (4.56).
$\unicode[STIX]{x1D70F}$
increases reading from the bottom of the figure to the top. The dash-dot line shows the location of the plate, solid lines show the numerical solution when the initial data are as given in (4.61), and dotted lines plot the far-field asymptotic form (4.56).
Figure 5. Graph of the evolution of
![]() $H^{\prime \prime }(\widehat{x},\unicode[STIX]{x1D70F})$
(related to the free surface displacement through (4.46), (4.43), (4.41) and (4.18)) against
$H^{\prime \prime }(\widehat{x},\unicode[STIX]{x1D70F})$
(related to the free surface displacement through (4.46), (4.43), (4.41) and (4.18)) against
![]() $\widehat{x}$
, showing agreement with the far-field asymptotic form (4.56) for the numerical solution of [EBVP], for
$\widehat{x}$
, showing agreement with the far-field asymptotic form (4.56) for the numerical solution of [EBVP], for
![]() $\unicode[STIX]{x1D70F}=0$
,
$\unicode[STIX]{x1D70F}=0$
,
![]() $\unicode[STIX]{x1D70F}=0.13$
,
$\unicode[STIX]{x1D70F}=0.13$
,
![]() $\unicode[STIX]{x1D70F}=0.25$
,
$\unicode[STIX]{x1D70F}=0.25$
,
![]() $\unicode[STIX]{x1D70F}=0.38$
,
$\unicode[STIX]{x1D70F}=0.38$
,
![]() $\unicode[STIX]{x1D70F}=0.5$
,
$\unicode[STIX]{x1D70F}=0.5$
,
![]() $\unicode[STIX]{x1D70F}=0.63$
,
$\unicode[STIX]{x1D70F}=0.63$
,
![]() $\unicode[STIX]{x1D70F}=0.75$
,
$\unicode[STIX]{x1D70F}=0.75$
,
![]() $\unicode[STIX]{x1D70F}=0.88$
and
$\unicode[STIX]{x1D70F}=0.88$
and
![]() $\unicode[STIX]{x1D70F}=1$
, where
$\unicode[STIX]{x1D70F}=1$
, where
![]() $\overline{\unicode[STIX]{x1D707}}=0$
and
$\overline{\unicode[STIX]{x1D707}}=0$
and
![]() $\unicode[STIX]{x1D6FC}=1.4$
. Here
$\unicode[STIX]{x1D6FC}=1.4$
. Here
![]() $\unicode[STIX]{x1D70F}$
increases reading from the bottom of the figure to the top. The dash-dot line shows the location of the plate, solid lines show the numerical solution when the initial data are as given in (4.61), and dotted lines plot the far-field asymptotic form (4.56).
$\unicode[STIX]{x1D70F}$
increases reading from the bottom of the figure to the top. The dash-dot line shows the location of the plate, solid lines show the numerical solution when the initial data are as given in (4.61), and dotted lines plot the far-field asymptotic form (4.56).
The first thing to observe concerning [EBVP], is that in the case when
![]() $\unicode[STIX]{x1D702}_{0}(\widehat{x})=0$
for
$\unicode[STIX]{x1D702}_{0}(\widehat{x})=0$
for
![]() $\widehat{x}\geqslant 0$
, then the solution to [EBVP] has the similarity structure
$\widehat{x}\geqslant 0$
, then the solution to [EBVP] has the similarity structure
where
![]() $\widehat{c}$
is the constant satisfying
$\widehat{c}$
is the constant satisfying
![]() $\widehat{H}^{\prime \prime }(\widehat{c})+\widehat{c}=0$
and
$\widehat{H}^{\prime \prime }(\widehat{c})+\widehat{c}=0$
and
![]() $\unicode[STIX]{x1D6E4}$
as in GNB (see (5.1)). This is anticipated from, and conforms with, the details in GNB (§ 5). We now proceed with the numerical solution of [EBVP].
$\unicode[STIX]{x1D6E4}$
as in GNB (see (5.1)). This is anticipated from, and conforms with, the details in GNB (§ 5). We now proceed with the numerical solution of [EBVP].
In solving [EBVP] numerically we must specify the initial free surface profile. For the following results we have taken
![]() $H^{\prime \prime }(\widehat{x},0)$
as
$H^{\prime \prime }(\widehat{x},0)$
as
We note that the original free surface displacement is then given by
Numerical solutions of [EBVP] are plotted in figures 2–5. In figure 2 we present the comparison between the free surface
![]() $H^{\prime \prime }(\widehat{x},\unicode[STIX]{x1D70F})$
calculated with zero initial data (shown in each plot as a dotted line) and the free surface
$H^{\prime \prime }(\widehat{x},\unicode[STIX]{x1D70F})$
calculated with zero initial data (shown in each plot as a dotted line) and the free surface
![]() $H^{\prime \prime }(\widehat{x},\unicode[STIX]{x1D70F})$
calculated with the initial free surface profile given in (4.61) (shown in each plot as a solid line) for the case
$H^{\prime \prime }(\widehat{x},\unicode[STIX]{x1D70F})$
calculated with the initial free surface profile given in (4.61) (shown in each plot as a solid line) for the case
![]() $\unicode[STIX]{x1D6FC}=1.4$
, with
$\unicode[STIX]{x1D6FC}=1.4$
, with
![]() $\overline{\unicode[STIX]{x1D707}}=1$
. It is clear to see, as may be anticipated from § 3.2, that, when initially perturbed, the free surface
$\overline{\unicode[STIX]{x1D707}}=1$
. It is clear to see, as may be anticipated from § 3.2, that, when initially perturbed, the free surface
![]() $H^{\prime \prime }(\widehat{x},\unicode[STIX]{x1D70F})$
collapses to the free surface corresponding to zero perturbation (which has the similarity solution (4.59)) as
$H^{\prime \prime }(\widehat{x},\unicode[STIX]{x1D70F})$
collapses to the free surface corresponding to zero perturbation (which has the similarity solution (4.59)) as
![]() $\unicode[STIX]{x1D70F}\rightarrow \infty$
, indicating that the problem [EBVP] is well-posed and stable in this case. This behaviour is typical of all pairs
$\unicode[STIX]{x1D70F}\rightarrow \infty$
, indicating that the problem [EBVP] is well-posed and stable in this case. This behaviour is typical of all pairs
![]() $(\unicode[STIX]{x1D6FC},\overline{\unicode[STIX]{x1D707}})$
tested in the range
$(\unicode[STIX]{x1D6FC},\overline{\unicode[STIX]{x1D707}})$
tested in the range
![]() $(\unicode[STIX]{x1D6FC},\overline{\unicode[STIX]{x1D707}})\in (\unicode[STIX]{x03C0}/4,\unicode[STIX]{x03C0}/2)\times \mathbb{R}^{+}$
, and of all initial free surface profiles
$(\unicode[STIX]{x1D6FC},\overline{\unicode[STIX]{x1D707}})\in (\unicode[STIX]{x03C0}/4,\unicode[STIX]{x03C0}/2)\times \mathbb{R}^{+}$
, and of all initial free surface profiles
![]() $\unicode[STIX]{x1D702}_{0}(\widehat{x})$
tested. As we decrease
$\unicode[STIX]{x1D702}_{0}(\widehat{x})$
tested. As we decrease
![]() $\overline{\unicode[STIX]{x1D707}}$
and take values with
$\overline{\unicode[STIX]{x1D707}}$
and take values with
![]() $\overline{\unicode[STIX]{x1D707}}<0$
we are unable to obtain numerically any converged solutions to [EBVP]. This indicates that the problem [EBVP] is ill-posed, which may also be anticipated from the theory presented in § 3.2. In figure 3 we present the comparison between the free surface
$\overline{\unicode[STIX]{x1D707}}<0$
we are unable to obtain numerically any converged solutions to [EBVP]. This indicates that the problem [EBVP] is ill-posed, which may also be anticipated from the theory presented in § 3.2. In figure 3 we present the comparison between the free surface
![]() $H^{\prime \prime }(\widehat{x},\unicode[STIX]{x1D70F})$
calculated with zero initial data (shown in each plot as a dotted line) and the free surface
$H^{\prime \prime }(\widehat{x},\unicode[STIX]{x1D70F})$
calculated with zero initial data (shown in each plot as a dotted line) and the free surface
![]() $H^{\prime \prime }(\widehat{x},\unicode[STIX]{x1D70F})$
calculated with the initial free surface profile given in (4.61) (shown in each plot as a solid line) for the case
$H^{\prime \prime }(\widehat{x},\unicode[STIX]{x1D70F})$
calculated with the initial free surface profile given in (4.61) (shown in each plot as a solid line) for the case
![]() $\unicode[STIX]{x1D6FC}=1.4$
, with
$\unicode[STIX]{x1D6FC}=1.4$
, with
![]() $\overline{\unicode[STIX]{x1D707}}=0$
. The case
$\overline{\unicode[STIX]{x1D707}}=0$
. The case
![]() $\overline{\unicode[STIX]{x1D707}}=0$
separates the regions on the
$\overline{\unicode[STIX]{x1D707}}=0$
separates the regions on the
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})$
plane where the problem [EBVP] is well-posed and stable (
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})$
plane where the problem [EBVP] is well-posed and stable (
![]() $\overline{\unicode[STIX]{x1D707}}>0$
) from ill-posed (
$\overline{\unicode[STIX]{x1D707}}>0$
) from ill-posed (
![]() $\overline{\unicode[STIX]{x1D707}}<0$
), with
$\overline{\unicode[STIX]{x1D707}}<0$
), with
![]() $\unicode[STIX]{x1D707}=0$
falling into the well-posed and stable case. Finally, figures 4 and 5 demonstrate the agreement of the numerical solution with the far-field asymptotic form in [EBVP] (4.56), at least to the graphical scales shown.
$\unicode[STIX]{x1D707}=0$
falling into the well-posed and stable case. Finally, figures 4 and 5 demonstrate the agreement of the numerical solution with the far-field asymptotic form in [EBVP] (4.56), at least to the graphical scales shown.
5 Conclusion
In this paper we have studied the well-posedness and stability of the problem [IBVP]. In particular, concerning the early stage motion close to the contact point, which was examined in detail in GNB, with respect to perturbations of amplitude
![]() $\unicode[STIX]{x1D6FF}\ll 1$
in initial data, located in the innermost asymptotic region of the solution to [IBVP] as
$\unicode[STIX]{x1D6FF}\ll 1$
in initial data, located in the innermost asymptotic region of the solution to [IBVP] as
![]() $t\rightarrow 0^{+}$
, for each pair
$t\rightarrow 0^{+}$
, for each pair
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,\unicode[STIX]{x03C0}/2)\times \mathbb{R}$
, where
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,\unicode[STIX]{x03C0}/2)\times \mathbb{R}$
, where
![]() $\unicode[STIX]{x1D707}=1+\unicode[STIX]{x1D70E}\tan \unicode[STIX]{x1D6FC}$
. This has enabled us to draw the following conclusions.
$\unicode[STIX]{x1D707}=1+\unicode[STIX]{x1D70E}\tan \unicode[STIX]{x1D6FC}$
. This has enabled us to draw the following conclusions.
-
(i)
 $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,\unicode[STIX]{x03C0}/2)\times \overline{\mathbb{R}}^{+}$
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,\unicode[STIX]{x03C0}/2)\times \overline{\mathbb{R}}^{+}$
Here, the initial boundary value problem [IBVP] is well-posed and stable with respect to perturbations in the initial data located in the inner region of the solution to [IBVP]. The time scale for decay is
 $t\gg O(\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x1D6FC}/\unicode[STIX]{x03C0}})$
.
$t\gg O(\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x1D6FC}/\unicode[STIX]{x03C0}})$
. -
(ii)
 $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,\unicode[STIX]{x03C0}/2)\times \mathbb{R}^{-}$
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,\unicode[STIX]{x03C0}/2)\times \mathbb{R}^{-}$
Here, the initial boundary value problem [IBVP] is ill-posed with respect to perturbations in initial data located in the inner region of the solution to [IBVP] with the time scale for the growth due to ill-posedness being
 $t\gg O(\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x1D6FC}/\unicode[STIX]{x03C0}})$
.
$t\gg O(\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x1D6FC}/\unicode[STIX]{x03C0}})$
.
In the above case (ii), when the solution to the unperturbed problem [IBVP] is ill-posed with respect to initial perturbations localised close to the contact point, we anticipate that the inclusion of weak surface tension effects in the model, leading to the problems [IBVP],
![]() $\text{[IBVP]}^{\prime }$
and
$\text{[IBVP]}^{\prime }$
and
![]() $\text{[IBVP]}^{\prime \prime }$
, will restore well-posedness, with the problem [IBVP] then becoming well-posed but unstable. The physical source of the ill-posedness of the problem [IBVP], is revealed on making the following observation. Returning to GNB (see §§ 4 and 5) we observe in the innermost regions that the leading-order displacement of the free surface has
$\text{[IBVP]}^{\prime \prime }$
, will restore well-posedness, with the problem [IBVP] then becoming well-posed but unstable. The physical source of the ill-posedness of the problem [IBVP], is revealed on making the following observation. Returning to GNB (see §§ 4 and 5) we observe in the innermost regions that the leading-order displacement of the free surface has
when
![]() $O(\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x1D6FC}/\unicode[STIX]{x03C0}})\ll t\ll 1$
. This represents a horizontal free surface accelerating vertically downwards, with dimensionless uniform acceleration of
$O(\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x1D6FC}/\unicode[STIX]{x03C0}})\ll t\ll 1$
. This represents a horizontal free surface accelerating vertically downwards, with dimensionless uniform acceleration of
![]() $-\unicode[STIX]{x1D70E}\tan \unicode[STIX]{x1D6FC}$
. With the dimensionless acceleration due to gravity on this localised block of fluid being unity, the situation is analogous to a local Rayleigh–Taylor problem (see, for example, Sharp Reference Sharp1984), which (in the absence of surface tension effects) would predict the horizontal free surface to be well-posed and stable to perturbations when
$-\unicode[STIX]{x1D70E}\tan \unicode[STIX]{x1D6FC}$
. With the dimensionless acceleration due to gravity on this localised block of fluid being unity, the situation is analogous to a local Rayleigh–Taylor problem (see, for example, Sharp Reference Sharp1984), which (in the absence of surface tension effects) would predict the horizontal free surface to be well-posed and stable to perturbations when
![]() $1>-\unicode[STIX]{x1D70E}\tan \unicode[STIX]{x1D6FC}$
, but ill-posed when
$1>-\unicode[STIX]{x1D70E}\tan \unicode[STIX]{x1D6FC}$
, but ill-posed when
![]() $1<-\unicode[STIX]{x1D70E}\tan \unicode[STIX]{x1D6FC}$
. Recalling that
$1<-\unicode[STIX]{x1D70E}\tan \unicode[STIX]{x1D6FC}$
. Recalling that
![]() $\unicode[STIX]{x1D707}=1+\unicode[STIX]{x1D70E}\tan \unicode[STIX]{x1D6FC}$
, this precisely accords with the cases above emerging from the detailed theory. This further supports our contention that the inclusion of weak surface tension effects will restore well-posedness in case (ii). In a more general context, we should note that, in both parts I and II of this pair of papers, the inner regions are driven principally by the matching conditions with the outer region, and in particular through the constant
$\unicode[STIX]{x1D707}=1+\unicode[STIX]{x1D70E}\tan \unicode[STIX]{x1D6FC}$
, this precisely accords with the cases above emerging from the detailed theory. This further supports our contention that the inclusion of weak surface tension effects will restore well-posedness in case (ii). In a more general context, we should note that, in both parts I and II of this pair of papers, the inner regions are driven principally by the matching conditions with the outer region, and in particular through the constant
![]() $A_{0}(\unicode[STIX]{x1D6FC})$
. Thus, the local flow structure, close to the initial contact point, in the early stages, will be the same for more general shaped surface piercing bodies which advance or retreat into an expanse of initially stationary fluid under gravity. Here
$A_{0}(\unicode[STIX]{x1D6FC})$
. Thus, the local flow structure, close to the initial contact point, in the early stages, will be the same for more general shaped surface piercing bodies which advance or retreat into an expanse of initially stationary fluid under gravity. Here
![]() $\unicode[STIX]{x1D6FC}$
will represent the body slope at the initial contact point when motion is initiated, and the detailed body shape is simply encompassed in the value of
$\unicode[STIX]{x1D6FC}$
will represent the body slope at the initial contact point when motion is initiated, and the detailed body shape is simply encompassed in the value of
![]() $A_{0}(\unicode[STIX]{x1D6FC})$
.
$A_{0}(\unicode[STIX]{x1D6FC})$
.
Acknowledgements
M.T.G. gratefully acknowledges financial support from EPSRC grant EP/H007830/1. We should like to thank all the referees for their detailed reading of the paper. Their comments have enabled us to significantly improve the paper.
Appendix A. Classification of the spectrum of [SP
 $(k)$
]
$(k)$
]
This appendix details the classification of the spectrum of [SP
![]() $(k)$
]. In § 3.2 we define the spectral problem [SP
$(k)$
]. In § 3.2 we define the spectral problem [SP
![]() $(k)$
] to be given by
$(k)$
] to be given by
with
![]() $k=-\unicode[STIX]{x1D706}^{2}/\unicode[STIX]{x1D707}$
(for
$k=-\unicode[STIX]{x1D706}^{2}/\unicode[STIX]{x1D707}$
(for
![]() $\unicode[STIX]{x1D707}\neq 0$
), and we require that solutions to [SP
$\unicode[STIX]{x1D707}\neq 0$
), and we require that solutions to [SP
![]() $(k)$
],
$(k)$
],
![]() $\overline{\unicode[STIX]{x1D6F7}}^{\prime }:\overline{{\mathcal{G}}}_{\infty }\rightarrow \mathbb{C}$
, have regularity given by (3.59). We define the spectrum of [SP
$\overline{\unicode[STIX]{x1D6F7}}^{\prime }:\overline{{\mathcal{G}}}_{\infty }\rightarrow \mathbb{C}$
, have regularity given by (3.59). We define the spectrum of [SP
![]() $(k)$
] to be given by
$(k)$
] to be given by
The set of eigenvalues of [SP
![]() $(k)$
] is
$(k)$
] is
![]() $\boldsymbol{S}^{d}$
, where
$\boldsymbol{S}^{d}$
, where
and the continuous spectrum of [SP
![]() $(k)$
] is
$(k)$
] is
![]() $\boldsymbol{S}^{c}$
, where
$\boldsymbol{S}^{c}$
, where
with the limits as
![]() $\overline{R}\rightarrow \infty$
considered as uniform for
$\overline{R}\rightarrow \infty$
considered as uniform for
![]() $-\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D703}\leqslant 0$
. Finally, we observe that
$-\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D703}\leqslant 0$
. Finally, we observe that
We now determine
![]() $\boldsymbol{S}$
. Following Needham (Reference Needham2012), we obtain the following results.
$\boldsymbol{S}$
. Following Needham (Reference Needham2012), we obtain the following results.
Theorem 1.
Proof. The proof requires that, for each
![]() $k\in \mathbb{C}\backslash R_{+}$
, we establish that [SP
$k\in \mathbb{C}\backslash R_{+}$
, we establish that [SP
![]() $(k)$
] has only the trivial solution. Let
$(k)$
] has only the trivial solution. Let
![]() $k\in \mathbb{C}\backslash R_{+}$
, and let
$k\in \mathbb{C}\backslash R_{+}$
, and let
![]() $\overline{\unicode[STIX]{x1D6F7}}^{\prime }:\overline{{\mathcal{G}}}_{\infty }\rightarrow \mathbb{C}$
be a solution to [SP
$\overline{\unicode[STIX]{x1D6F7}}^{\prime }:\overline{{\mathcal{G}}}_{\infty }\rightarrow \mathbb{C}$
be a solution to [SP
![]() $(k)$
]. Take any
$(k)$
]. Take any
![]() $R_{0}>0$
and set
$R_{0}>0$
and set
![]() $\overline{{\mathcal{G}}}_{R_{0}}=\overline{{\mathcal{G}}}_{\infty }\backslash (R_{0},\infty )\times [-\unicode[STIX]{x1D6FC},0]$
, and
$\overline{{\mathcal{G}}}_{R_{0}}=\overline{{\mathcal{G}}}_{\infty }\backslash (R_{0},\infty )\times [-\unicode[STIX]{x1D6FC},0]$
, and
![]() $\unicode[STIX]{x2202}{\mathcal{G}}=\{(\overline{R},\unicode[STIX]{x1D703}):0\leqslant \overline{R}\leqslant R_{0},\unicode[STIX]{x1D703}=0\}\cup \{(\overline{R},\unicode[STIX]{x1D703}):\overline{R}=R_{0},-\unicode[STIX]{x1D6FC}<\unicode[STIX]{x1D703}<0\}\cup \{(\overline{R},\unicode[STIX]{x1D703}):0\leqslant \overline{R}\leqslant R_{0},\unicode[STIX]{x1D703}=-\unicode[STIX]{x1D6FC}\}$
, then Green’s Theorem (see, for example, Kaplan (Reference Kaplan2002)), along with the regularity (3.59) and (A 1), gives
$\unicode[STIX]{x2202}{\mathcal{G}}=\{(\overline{R},\unicode[STIX]{x1D703}):0\leqslant \overline{R}\leqslant R_{0},\unicode[STIX]{x1D703}=0\}\cup \{(\overline{R},\unicode[STIX]{x1D703}):\overline{R}=R_{0},-\unicode[STIX]{x1D6FC}<\unicode[STIX]{x1D703}<0\}\cup \{(\overline{R},\unicode[STIX]{x1D703}):0\leqslant \overline{R}\leqslant R_{0},\unicode[STIX]{x1D703}=-\unicode[STIX]{x1D6FC}\}$
, then Green’s Theorem (see, for example, Kaplan (Reference Kaplan2002)), along with the regularity (3.59) and (A 1), gives
where superscript
![]() $^{\ast }$
denotes complex conjugation. It follows from (A 10) and (A 2) that
$^{\ast }$
denotes complex conjugation. It follows from (A 10) and (A 2) that
which becomes, using (A 3),
for each
![]() $R_{0}>0$
. We now introduce
$R_{0}>0$
. We now introduce
![]() $u$
and
$u$
and
![]() $v$
, where
$v$
, where
after which we obtain from (A 12)
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\overline{{\mathcal{G}}}_{R_{0}}}\int \left(|\overline{\unicode[STIX]{x1D6F7}}_{\overline{R}}^{\prime }|^{2}+\left|\frac{1}{\overline{R}}\overline{\unicode[STIX]{x1D6F7}}_{\unicode[STIX]{x1D703}}^{\prime }\right|^{2}\right)\overline{R}\,\text{d}\overline{R}\,\text{d}\unicode[STIX]{x1D703}-k\int _{0}^{R_{0}}(|\overline{\unicode[STIX]{x1D6F7}}^{\prime }|^{2})_{\unicode[STIX]{x1D703}=0}\,\text{d}\overline{R}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2}R_{0}\frac{\text{d}}{\text{d}R_{0}}\left\{\int _{-\unicode[STIX]{x1D6FC}}^{0}(|\overline{\unicode[STIX]{x1D6F7}}^{\prime }|_{\overline{R}=R_{0}}^{2}\,\text{d}\unicode[STIX]{x1D703})\right\}+\text{i}R_{0}\int _{-\unicode[STIX]{x1D6FC}}^{0}(uv_{\overline{R}}-u_{\overline{R}}v)_{\overline{R}=R_{0}}\,\text{d}\unicode[STIX]{x1D703}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\overline{{\mathcal{G}}}_{R_{0}}}\int \left(|\overline{\unicode[STIX]{x1D6F7}}_{\overline{R}}^{\prime }|^{2}+\left|\frac{1}{\overline{R}}\overline{\unicode[STIX]{x1D6F7}}_{\unicode[STIX]{x1D703}}^{\prime }\right|^{2}\right)\overline{R}\,\text{d}\overline{R}\,\text{d}\unicode[STIX]{x1D703}-k\int _{0}^{R_{0}}(|\overline{\unicode[STIX]{x1D6F7}}^{\prime }|^{2})_{\unicode[STIX]{x1D703}=0}\,\text{d}\overline{R}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2}R_{0}\frac{\text{d}}{\text{d}R_{0}}\left\{\int _{-\unicode[STIX]{x1D6FC}}^{0}(|\overline{\unicode[STIX]{x1D6F7}}^{\prime }|_{\overline{R}=R_{0}}^{2}\,\text{d}\unicode[STIX]{x1D703})\right\}+\text{i}R_{0}\int _{-\unicode[STIX]{x1D6FC}}^{0}(uv_{\overline{R}}-u_{\overline{R}}v)_{\overline{R}=R_{0}}\,\text{d}\unicode[STIX]{x1D703}.\end{eqnarray}$$
Taking the real part of (A 14) gives
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\overline{{\mathcal{G}}}_{R_{0}}}\int \left(|\overline{\unicode[STIX]{x1D6F7}}_{\overline{R}}^{\prime }|^{2}+\left|\frac{1}{\overline{R}}\overline{\unicode[STIX]{x1D6F7}}_{\unicode[STIX]{x1D703}}^{\prime }\right|^{2}\right)\overline{R}\,\text{d}\overline{R}\,\text{d}\unicode[STIX]{x1D703}-\text{Re}(k)\int _{0}^{R_{0}}(|\overline{\unicode[STIX]{x1D6F7}}^{\prime }|^{2})_{\unicode[STIX]{x1D703}=0}\,\text{d}\overline{R}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2}R_{0}\frac{\text{d}}{\text{d}R_{0}}\left\{\int _{-\unicode[STIX]{x1D6FC}}^{0}(|\overline{\unicode[STIX]{x1D6F7}}^{\prime }|_{\overline{R}=R_{0}}^{2})\,\text{d}\unicode[STIX]{x1D703}\right\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\overline{{\mathcal{G}}}_{R_{0}}}\int \left(|\overline{\unicode[STIX]{x1D6F7}}_{\overline{R}}^{\prime }|^{2}+\left|\frac{1}{\overline{R}}\overline{\unicode[STIX]{x1D6F7}}_{\unicode[STIX]{x1D703}}^{\prime }\right|^{2}\right)\overline{R}\,\text{d}\overline{R}\,\text{d}\unicode[STIX]{x1D703}-\text{Re}(k)\int _{0}^{R_{0}}(|\overline{\unicode[STIX]{x1D6F7}}^{\prime }|^{2})_{\unicode[STIX]{x1D703}=0}\,\text{d}\overline{R}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2}R_{0}\frac{\text{d}}{\text{d}R_{0}}\left\{\int _{-\unicode[STIX]{x1D6FC}}^{0}(|\overline{\unicode[STIX]{x1D6F7}}^{\prime }|_{\overline{R}=R_{0}}^{2})\,\text{d}\unicode[STIX]{x1D703}\right\},\end{eqnarray}$$
for each
![]() $R_{0}>0$
. Using (3.63) we can now write the right-hand side of (A 15), in the limit
$R_{0}>0$
. Using (3.63) we can now write the right-hand side of (A 15), in the limit
![]() $R_{0}\rightarrow \infty$
, as
$R_{0}\rightarrow \infty$
, as
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{2}R_{0}\frac{\text{d}}{\text{d}R_{0}}\left\{\int _{-\unicode[STIX]{x1D6FC}}^{0}(|\overline{\unicode[STIX]{x1D6F7}}^{\prime }|_{\overline{R}=R_{0}}^{2}\,\text{d}\unicode[STIX]{x1D703})\right\}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2}R_{0}\frac{\text{d}}{\text{d}R_{0}}\left\{\int _{-\unicode[STIX]{x1D6FC}}^{0}\left(|a_{k}|^{2}\frac{1}{R_{0}^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}}}\cos ^{2}\frac{\unicode[STIX]{x03C0}}{2\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D703}+\unicode[STIX]{x1D6FC})+O\left(\frac{1}{R_{0}^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}+1}}\right)\right)\,\text{d}\unicode[STIX]{x1D703}\right\}\nonumber\\ \displaystyle & & \displaystyle \quad =-\frac{\unicode[STIX]{x03C0}}{4}|a_{k}|^{2}\frac{1}{R_{0}^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}}}+O\left(\frac{1}{R_{0}^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}+1}}\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{2}R_{0}\frac{\text{d}}{\text{d}R_{0}}\left\{\int _{-\unicode[STIX]{x1D6FC}}^{0}(|\overline{\unicode[STIX]{x1D6F7}}^{\prime }|_{\overline{R}=R_{0}}^{2}\,\text{d}\unicode[STIX]{x1D703})\right\}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2}R_{0}\frac{\text{d}}{\text{d}R_{0}}\left\{\int _{-\unicode[STIX]{x1D6FC}}^{0}\left(|a_{k}|^{2}\frac{1}{R_{0}^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}}}\cos ^{2}\frac{\unicode[STIX]{x03C0}}{2\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D703}+\unicode[STIX]{x1D6FC})+O\left(\frac{1}{R_{0}^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}+1}}\right)\right)\,\text{d}\unicode[STIX]{x1D703}\right\}\nonumber\\ \displaystyle & & \displaystyle \quad =-\frac{\unicode[STIX]{x03C0}}{4}|a_{k}|^{2}\frac{1}{R_{0}^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}}}+O\left(\frac{1}{R_{0}^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}+1}}\right),\end{eqnarray}$$
which is bounded as
![]() $R_{0}\rightarrow \infty$
. Since
$R_{0}\rightarrow \infty$
. Since
![]() $\text{Re}(k)\leqslant 0$
, it then follows from (A 15) that
$\text{Re}(k)\leqslant 0$
, it then follows from (A 15) that
and so the left-hand side of (A 17) is bounded and non-decreasing as
![]() $R_{0}\rightarrow \infty$
, and thus has a finite non-negative limit as
$R_{0}\rightarrow \infty$
, and thus has a finite non-negative limit as
![]() $R_{0}\rightarrow \infty$
, so that
$R_{0}\rightarrow \infty$
, so that
for some
![]() $\unicode[STIX]{x1D6FD}\geqslant 0$
. However, it now follows from (A 16) to (A 18) that
$\unicode[STIX]{x1D6FD}\geqslant 0$
. However, it now follows from (A 16) to (A 18) that
![]() $\unicode[STIX]{x1D6FD}\leqslant 0$
, and so we conclude that
$\unicode[STIX]{x1D6FD}\leqslant 0$
, and so we conclude that
![]() $\unicode[STIX]{x1D6FD}=0$
. We then have from (A 18) that
$\unicode[STIX]{x1D6FD}=0$
. We then have from (A 18) that
for all
![]() $R_{0}>0$
. The condition (A 19) (along with regularity (3.59)) then requires that
$R_{0}>0$
. The condition (A 19) (along with regularity (3.59)) then requires that
![]() $\overline{\unicode[STIX]{x1D6F7}}^{\prime }(\overline{R},\unicode[STIX]{x1D703})=C$
for all
$\overline{\unicode[STIX]{x1D6F7}}^{\prime }(\overline{R},\unicode[STIX]{x1D703})=C$
for all
![]() $(\overline{R},\unicode[STIX]{x1D703})\in [0,\infty )\times [-\unicode[STIX]{x1D6FC},0]$
, for some constant
$(\overline{R},\unicode[STIX]{x1D703})\in [0,\infty )\times [-\unicode[STIX]{x1D6FC},0]$
, for some constant
![]() $C\in \mathbb{C}$
. However, since
$C\in \mathbb{C}$
. However, since
![]() $k\neq 0$
, we have from (A 3) that
$k\neq 0$
, we have from (A 3) that
![]() $C=0$
, so that
$C=0$
, so that
![]() $\overline{\unicode[STIX]{x1D6F7}}^{\prime }(\overline{R},\unicode[STIX]{x1D703})=0$
for all
$\overline{\unicode[STIX]{x1D6F7}}^{\prime }(\overline{R},\unicode[STIX]{x1D703})=0$
for all
![]() $(\overline{R},\unicode[STIX]{x1D703})\in [0,\infty )\times [-\unicode[STIX]{x1D6FC},0]$
, which is the trivial solution, and the proof is complete. ☐
$(\overline{R},\unicode[STIX]{x1D703})\in [0,\infty )\times [-\unicode[STIX]{x1D6FC},0]$
, which is the trivial solution, and the proof is complete. ☐
Theorem 2.
Proof. Let
![]() $k\in R_{+}\backslash (\mathbb{R}^{+}\cup \{0\})$
, and
$k\in R_{+}\backslash (\mathbb{R}^{+}\cup \{0\})$
, and
![]() $\overline{\unicode[STIX]{x1D6F7}}^{\prime }:\overline{{\mathcal{G}}}_{\infty }\rightarrow \mathbb{C}$
be a solution to [SP
$\overline{\unicode[STIX]{x1D6F7}}^{\prime }:\overline{{\mathcal{G}}}_{\infty }\rightarrow \mathbb{C}$
be a solution to [SP
![]() $(k)$
]. We must show that
$(k)$
]. We must show that
![]() $\overline{\unicode[STIX]{x1D6F7}}^{\prime }$
is the trivial solution. We have from (3.63) that
$\overline{\unicode[STIX]{x1D6F7}}^{\prime }$
is the trivial solution. We have from (3.63) that
as
![]() $\overline{R}\rightarrow \infty$
, uniformly for
$\overline{R}\rightarrow \infty$
, uniformly for
![]() $-\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D703}\leqslant 0$
, with
$-\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D703}\leqslant 0$
, with
![]() $a\in \mathbb{C}$
being a non-zero constant. We also have from (A 14), that
$a\in \mathbb{C}$
being a non-zero constant. We also have from (A 14), that
and
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\overline{{\mathcal{G}}}_{R_{0}}}\int \left(|\overline{\unicode[STIX]{x1D6F7}}_{\overline{R}}^{\prime }|^{2}+\left|\frac{1}{\overline{R}}\overline{\unicode[STIX]{x1D6F7}}_{\unicode[STIX]{x1D703}}^{\prime }\right|^{2}\right)\overline{R}\,\text{d}\overline{R}\,\text{d}\unicode[STIX]{x1D703}-\text{Re}(k)\int _{0}^{R_{0}}(|\overline{\unicode[STIX]{x1D6F7}}^{\prime }|^{2})_{\unicode[STIX]{x1D703}=0}\,\text{d}\overline{R}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2}R_{0}\frac{\text{d}}{\text{d}R_{0}}\left\{\int _{-\unicode[STIX]{x1D6FC}}^{0}(|\overline{\unicode[STIX]{x1D6F7}}^{\prime }|^{2})_{\overline{R}=R_{0}}\,\text{d}\unicode[STIX]{x1D703}\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\overline{{\mathcal{G}}}_{R_{0}}}\int \left(|\overline{\unicode[STIX]{x1D6F7}}_{\overline{R}}^{\prime }|^{2}+\left|\frac{1}{\overline{R}}\overline{\unicode[STIX]{x1D6F7}}_{\unicode[STIX]{x1D703}}^{\prime }\right|^{2}\right)\overline{R}\,\text{d}\overline{R}\,\text{d}\unicode[STIX]{x1D703}-\text{Re}(k)\int _{0}^{R_{0}}(|\overline{\unicode[STIX]{x1D6F7}}^{\prime }|^{2})_{\unicode[STIX]{x1D703}=0}\,\text{d}\overline{R}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2}R_{0}\frac{\text{d}}{\text{d}R_{0}}\left\{\int _{-\unicode[STIX]{x1D6FC}}^{0}(|\overline{\unicode[STIX]{x1D6F7}}^{\prime }|^{2})_{\overline{R}=R_{0}}\,\text{d}\unicode[STIX]{x1D703}\right\}.\end{eqnarray}$$
Now, via (A 21), we have that
Since
![]() $\text{Im}(k)\neq 0$
it then follows from (A 22) that
$\text{Im}(k)\neq 0$
it then follows from (A 22) that
and so
for all
![]() $R_{0}>0$
. Next, considering (A 23), (A 26), and (A 16), we have that
$R_{0}>0$
. Next, considering (A 23), (A 26), and (A 16), we have that
It then immediately follows that
![]() $\overline{\unicode[STIX]{x1D6F7}}^{\prime }(\overline{R},\unicode[STIX]{x1D703})=0$
, for all
$\overline{\unicode[STIX]{x1D6F7}}^{\prime }(\overline{R},\unicode[STIX]{x1D703})=0$
, for all
![]() $(\overline{R},\unicode[STIX]{x1D703})\in [0,\infty )\times [-\unicode[STIX]{x1D6FC},0]$
, which is the trivial solution, and the proof is complete.☐
$(\overline{R},\unicode[STIX]{x1D703})\in [0,\infty )\times [-\unicode[STIX]{x1D6FC},0]$
, which is the trivial solution, and the proof is complete.☐
In fact
![]() $\boldsymbol{S}=\mathbb{R}^{+}\cup \{0\}$
. Clearly,
$\boldsymbol{S}=\mathbb{R}^{+}\cup \{0\}$
. Clearly,
![]() $0\in \boldsymbol{S}$
, since when
$0\in \boldsymbol{S}$
, since when
![]() $k=0$
,
$k=0$
,
![]() $\overline{\unicode[STIX]{x1D6F7}}^{\prime }(\overline{R},\unicode[STIX]{x1D703})=1$
for all
$\overline{\unicode[STIX]{x1D6F7}}^{\prime }(\overline{R},\unicode[STIX]{x1D703})=1$
for all
![]() $(\overline{R},\unicode[STIX]{x1D703})\in [0,\infty )\times [-\unicode[STIX]{x1D6FC},0]$
, solves
$(\overline{R},\unicode[STIX]{x1D703})\in [0,\infty )\times [-\unicode[STIX]{x1D6FC},0]$
, solves
![]() $[SP(0)]$
. Moreover John (Reference John1948) has established that
$[SP(0)]$
. Moreover John (Reference John1948) has established that
![]() $k\in \boldsymbol{S}$
for all
$k\in \boldsymbol{S}$
for all
![]() $k\in \mathbb{R}^{+}$
, and in addition that,
$k\in \mathbb{R}^{+}$
, and in addition that,
![]() $\boldsymbol{S}^{c}=\mathbb{R}^{+}\cup (0)$
whilst
$\boldsymbol{S}^{c}=\mathbb{R}^{+}\cup (0)$
whilst
![]() $\boldsymbol{S}^{d}=\varnothing$
.
$\boldsymbol{S}^{d}=\varnothing$
.