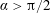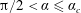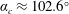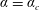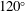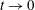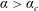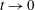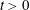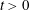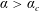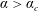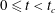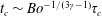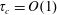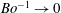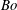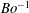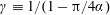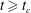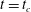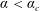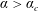1 Introduction
Fluid flows driven by moving solid boundaries occur in many practical situations, the most obvious being those associated with the motion of ships and other floating bodies. In this series of papers we have studied various aspects of a two-dimensional model problem that has direct relevance to the motion of ships, namely the irrotational flow of a finite layer of inviscid fluid generated by the motion of a flat, rigid, bounding wall (King & Needham Reference King and Needham1994; Needham, Billingham & King Reference Needham, Billingham and King2007; Needham, Chamberlain & Billingham Reference Needham, Chamberlain and Billingham2008). In Needham et al. (Reference Needham, Chamberlain and Billingham2008), hereafter referred to as Part 3, we used formal, small-time matched asymptotic expansions to study the free surface flow generated when the plate is inclined at an external angle
![]() $\unicode[STIX]{x1D6FC}$
to the horizontal and driven into the fluid with a constant, horizontal acceleration. It is this problem that we study here, but we will also include the effect of surface tension on the flow. We do this because we found strong numerical evidence that for
$\unicode[STIX]{x1D6FC}$
to the horizontal and driven into the fluid with a constant, horizontal acceleration. It is this problem that we study here, but we will also include the effect of surface tension on the flow. We do this because we found strong numerical evidence that for
![]() $\unicode[STIX]{x1D6FC}$
greater than a critical angle
$\unicode[STIX]{x1D6FC}$
greater than a critical angle
![]() $\unicode[STIX]{x1D6FC}_{c}\approx 102.6^{\circ }$
, in the absence of surface tension, no small-time asymptotic solution of the initial boundary value problem exists as we posed it for any time
$\unicode[STIX]{x1D6FC}_{c}\approx 102.6^{\circ }$
, in the absence of surface tension, no small-time asymptotic solution of the initial boundary value problem exists as we posed it for any time
![]() $t>0$
. This unphysical state of affairs does not persist for
$t>0$
. This unphysical state of affairs does not persist for
![]() $\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D6FC}_{c}$
. We can put the situation into context by noting that when
$\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D6FC}_{c}$
. We can put the situation into context by noting that when
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{c}$
we found strong numerical evidence for the existence of a
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{c}$
we found strong numerical evidence for the existence of a
![]() $120^{\circ }$
corner on the free surface at leading order as
$120^{\circ }$
corner on the free surface at leading order as
![]() $t\rightarrow 0$
. We constructed a local solution of this form, which we later generalised (Needham & Billingham Reference Needham and Billingham2009). This situation is an unsteady analogue of steady gravity waves, the highest of which is topped by a locally identical
$t\rightarrow 0$
. We constructed a local solution of this form, which we later generalised (Needham & Billingham Reference Needham and Billingham2009). This situation is an unsteady analogue of steady gravity waves, the highest of which is topped by a locally identical
![]() $120^{\circ }$
corner (Michell Reference Michell1893).
$120^{\circ }$
corner (Michell Reference Michell1893).
The likely non-existence of a solution for
![]() $\unicode[STIX]{x1D6FC}>\unicode[STIX]{x1D6FC}_{c}$
suggests that some of the physics neglected in the original model needs to be reinstated, and the obvious candidate is surface tension. A real free surface cannot support the infinite curvature of a
$\unicode[STIX]{x1D6FC}>\unicode[STIX]{x1D6FC}_{c}$
suggests that some of the physics neglected in the original model needs to be reinstated, and the obvious candidate is surface tension. A real free surface cannot support the infinite curvature of a
![]() $120^{\circ }$
corner because surface tension forces are proportional to curvature, so we have good reason to believe that the form of the solution will be strongly affected by surface tension when
$120^{\circ }$
corner because surface tension forces are proportional to curvature, so we have good reason to believe that the form of the solution will be strongly affected by surface tension when
![]() $\unicode[STIX]{x1D6FC}$
is close to
$\unicode[STIX]{x1D6FC}$
is close to
![]() $\unicode[STIX]{x1D6FC}_{c}$
. We speculate (correctly) that surface tension must therefore be important when
$\unicode[STIX]{x1D6FC}_{c}$
. We speculate (correctly) that surface tension must therefore be important when
![]() $\unicode[STIX]{x1D6FC}>\unicode[STIX]{x1D6FC}_{c}$
, and indeed, at small enough times, for all
$\unicode[STIX]{x1D6FC}>\unicode[STIX]{x1D6FC}_{c}$
, and indeed, at small enough times, for all
![]() $\unicode[STIX]{x1D6FC}>\unicode[STIX]{x03C0}/2$
.
$\unicode[STIX]{x1D6FC}>\unicode[STIX]{x03C0}/2$
.
A key point to consider throughout this paper is that we have no comment to make on the stability of any of the solutions that we discuss. The solution emerges from a simple, well-defined initial condition and develops the structures that we discuss below. Although we could speculate about the stability of solutions with
![]() $\unicode[STIX]{x1D6FC}$
close to
$\unicode[STIX]{x1D6FC}$
close to
![]() $\unicode[STIX]{x1D6FC}_{c}$
, in which case a high curvature region develops on the free surface, we have not done so, as we do not believe that this is the most important aspect of the system that we are studying. For an example of a similar system where stability of the free surface is a crucial factor in understanding the flow, see Gallagher, Needham & Billingham (Reference Gallagher, Needham and Billingham2017).
$\unicode[STIX]{x1D6FC}_{c}$
, in which case a high curvature region develops on the free surface, we have not done so, as we do not believe that this is the most important aspect of the system that we are studying. For an example of a similar system where stability of the free surface is a crucial factor in understanding the flow, see Gallagher, Needham & Billingham (Reference Gallagher, Needham and Billingham2017).
Note also that for
![]() $0\leqslant Bo^{-1}\ll 1$
the initial boundary value problem presented in this paper is singular as
$0\leqslant Bo^{-1}\ll 1$
the initial boundary value problem presented in this paper is singular as
![]() $t\rightarrow 0$
, as shown by the emergence of the asymptotic structures described below, and is therefore not amenable to direct numerical solution. In principle it is possible to solve the full problem numerically from
$t\rightarrow 0$
, as shown by the emergence of the asymptotic structures described below, and is therefore not amenable to direct numerical solution. In principle it is possible to solve the full problem numerically from
![]() $t=t_{0}\ll 1$
, using the asymptotic solution developed in this paper as the initial condition, but this would not lead to any more insight than that which we gain by considering the asymptotic solution directly, either for
$t=t_{0}\ll 1$
, using the asymptotic solution developed in this paper as the initial condition, but this would not lead to any more insight than that which we gain by considering the asymptotic solution directly, either for
![]() $t\ll 1$
or
$t\ll 1$
or
![]() $0<Bo^{-1}\ll 1$
.
$0<Bo^{-1}\ll 1$
.
We begin in § 2 by setting up the initial boundary value problem that governs the motion of the fluid, including the effect of surface tension, and briefly recapitulate the relevant key results when surface tension is neglected (for more details, see Part 3). In § 3 we elucidate the asymptotic structure of the solution when the Bond number is large (capillary length much smaller than the initial depth of the fluid – weak surface tension), focusing on the unsteady problem in the small, inner region, close to the contact line where the free surface meets the plate. We are able to determine the structure of the small-time asymptotic solution of this problem (§ 3.1) and, by solving the leading-order problem numerically, provide strong evidence that the solution exists, at least for some finite time, in particular when
![]() $\unicode[STIX]{x1D6FC}>\unicode[STIX]{x1D6FC}_{c}$
. This supports our conjecture that neglecting surface tension is a singular perturbation for
$\unicode[STIX]{x1D6FC}>\unicode[STIX]{x1D6FC}_{c}$
. This supports our conjecture that neglecting surface tension is a singular perturbation for
![]() $\unicode[STIX]{x1D6FC}>\unicode[STIX]{x1D6FC}_{c}$
. In § 3.2 we present numerical solutions of the unsteady inner problem. These show that for all
$\unicode[STIX]{x1D6FC}>\unicode[STIX]{x1D6FC}_{c}$
. In § 3.2 we present numerical solutions of the unsteady inner problem. These show that for all
![]() $\unicode[STIX]{x1D6FC}>\unicode[STIX]{x03C0}/2$
a capillary wave is generated on the free surface ahead of a wavecrest. When
$\unicode[STIX]{x1D6FC}>\unicode[STIX]{x03C0}/2$
a capillary wave is generated on the free surface ahead of a wavecrest. When
![]() $\unicode[STIX]{x1D6FC}<\unicode[STIX]{x1D6FC}_{c}$
, this wave decays in amplitude as the free surface evolves. However, when
$\unicode[STIX]{x1D6FC}<\unicode[STIX]{x1D6FC}_{c}$
, this wave decays in amplitude as the free surface evolves. However, when
![]() $\unicode[STIX]{x1D6FC}>\unicode[STIX]{x1D6FC}_{c}$
the amplitude of the capillary wave grows and eventually leads to self-intersection of the free surface (in practice, entrainment of air) close to a point of high curvature at some small but finite time (we refer to this as pinch-off). These capillary waves are an unsteady analogue of the parasitic capillary waves that can be generated ahead of steadily propagating, periodic, capillary–gravity waves when surface tension is weak (for example, Longuet-Higgins Reference Longuet-Higgins1992; Lin & Rockwell Reference Lin and Rockwell1995; Deike, Popinet & Kendall Melville Reference Deike, Popinet and Kendall Melville2015).
$\unicode[STIX]{x1D6FC}>\unicode[STIX]{x1D6FC}_{c}$
the amplitude of the capillary wave grows and eventually leads to self-intersection of the free surface (in practice, entrainment of air) close to a point of high curvature at some small but finite time (we refer to this as pinch-off). These capillary waves are an unsteady analogue of the parasitic capillary waves that can be generated ahead of steadily propagating, periodic, capillary–gravity waves when surface tension is weak (for example, Longuet-Higgins Reference Longuet-Higgins1992; Lin & Rockwell Reference Lin and Rockwell1995; Deike, Popinet & Kendall Melville Reference Deike, Popinet and Kendall Melville2015).
We also briefly present a comparison with some experimental results in § 4 (these will be reported in more detail elsewhere), which demonstrate good agreement with the unsteady asymptotic solution, at least for a case where the dynamic contact angle is approximately constant, an assumption that we make in this paper. We conclude in § 5.
2 The initial boundary value problem
2.1 Governing equations
We consider an initially stationary, semi-infinite layer of inviscid, incompressible fluid with constant depth
![]() $h$
, bounded below by a rigid, horizontal surface, and bounded to the left by a rigid, flat plate inclined to the horizontal at an angle
$h$
, bounded below by a rigid, horizontal surface, and bounded to the left by a rigid, flat plate inclined to the horizontal at an angle
![]() $\unicode[STIX]{x1D6FC}>\unicode[STIX]{x03C0}/2$
. The initially horizontal free surface extends to infinity away from the inclined plate. When time
$\unicode[STIX]{x1D6FC}>\unicode[STIX]{x03C0}/2$
. The initially horizontal free surface extends to infinity away from the inclined plate. When time
![]() $t\geqslant 0$
, the inclined plate is driven into the fluid with a constant horizontal acceleration of magnitude
$t\geqslant 0$
, the inclined plate is driven into the fluid with a constant horizontal acceleration of magnitude
![]() $a$
. Throughout this paper, we will assume that the contact angle (strictly speaking, the apparent contact angle) is constant and equal to
$a$
. Throughout this paper, we will assume that the contact angle (strictly speaking, the apparent contact angle) is constant and equal to
![]() $\unicode[STIX]{x1D6FC}$
, independent of contact line velocity, so that the initially horizontal free surface is in equilibrium. We will consider the case of an arbitrary constant contact angle in a later paper, with the initial shape of the free surface a meniscus at equilibrium. The assumption that the contact angle does not vary with the velocity of the contact line is a strong one, but there is no experimentally validated model that gives accurate results for the unsteady motion of a contact line across a solid surface, particularly a rough surface. Moreover, the experimental results of Korsukova (Reference Korsukova2014), which we will discuss in some detail below, show that the solution when the contact angle is constant and equal to
$\unicode[STIX]{x1D6FC}$
, independent of contact line velocity, so that the initially horizontal free surface is in equilibrium. We will consider the case of an arbitrary constant contact angle in a later paper, with the initial shape of the free surface a meniscus at equilibrium. The assumption that the contact angle does not vary with the velocity of the contact line is a strong one, but there is no experimentally validated model that gives accurate results for the unsteady motion of a contact line across a solid surface, particularly a rough surface. Moreover, the experimental results of Korsukova (Reference Korsukova2014), which we will discuss in some detail below, show that the solution when the contact angle is constant and equal to
![]() $\unicode[STIX]{x1D6FC}$
is qualitatively similar to real experimental solutions, and that the measured contact angle remains close to constant.
$\unicode[STIX]{x1D6FC}$
is qualitatively similar to real experimental solutions, and that the measured contact angle remains close to constant.
We non-dimensionalise the problem using
![]() $h$
and the gravitational acceleration,
$h$
and the gravitational acceleration,
![]() $g$
, and work in a frame of reference in which the moving, inclined plate is fixed. The velocity field relative to the stationary bottom is
$g$
, and work in a frame of reference in which the moving, inclined plate is fixed. The velocity field relative to the stationary bottom is
![]() $\boldsymbol{u}(x,y,t)=\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}(x,y,t)$
, where
$\boldsymbol{u}(x,y,t)=\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}(x,y,t)$
, where
![]() $\unicode[STIX]{x1D719}$
is the velocity potential, and
$\unicode[STIX]{x1D719}$
is the velocity potential, and
![]() $(x,y)$
is a Cartesian coordinate system with horizontal
$(x,y)$
is a Cartesian coordinate system with horizontal
![]() $x$
-axis and origin at the initial contact point between the free surface and the plate, as shown in figure 1.
$x$
-axis and origin at the initial contact point between the free surface and the plate, as shown in figure 1.

Figure 1. The Cartesian coordinate system, fixed in the inclined plate.
The initial boundary value problem (IBVP) whose solution we wish to study is therefore given by conservation of mass,
impermeability of the inclined plate,
where
![]() $\unicode[STIX]{x1D70E}\equiv a/g$
is the dimensionless acceleration of the plate, no penetration at the bottom of the fluid,
$\unicode[STIX]{x1D70E}\equiv a/g$
is the dimensionless acceleration of the plate, no penetration at the bottom of the fluid,
the kinematic condition on the free surface,
the Bernoulli condition (constant pressure) at the free surface,
the contact angle condition,
no flow at infinity,
and the fluid initially at rest in equilibrium,
In these equations,
![]() $y=\unicode[STIX]{x1D702}(x,t)$
is the position of the free surface,
$y=\unicode[STIX]{x1D702}(x,t)$
is the position of the free surface,
![]() $(x_{c}(t),y_{c}(t))$
is the position of the contact line on the inclined plate and
$(x_{c}(t),y_{c}(t))$
is the position of the contact line on the inclined plate and
![]() $Bo\equiv \unicode[STIX]{x1D70C}gh^{2}/T$
is the Bond number, where
$Bo\equiv \unicode[STIX]{x1D70C}gh^{2}/T$
is the Bond number, where
![]() $\unicode[STIX]{x1D70C}$
is the constant density of the fluid and
$\unicode[STIX]{x1D70C}$
is the constant density of the fluid and
![]() $T$
the constant surface tension coefficient (in order to find solutions numerically later in the paper, we will use a Lagrangian formulation, and not implicitly assume either that
$T$
the constant surface tension coefficient (in order to find solutions numerically later in the paper, we will use a Lagrangian formulation, and not implicitly assume either that
![]() $y$
at the free surface is a single-valued function of
$y$
at the free surface is a single-valued function of
![]() $x$
or that
$x$
or that
![]() $x\geqslant x_{c}(t)$
on the free surface, but for ease of presentation, we do so here). Note that we can also write
$x\geqslant x_{c}(t)$
on the free surface, but for ease of presentation, we do so here). Note that we can also write
![]() $Bo^{-1}\equiv h_{c}^{2}/h^{2}$
, where
$Bo^{-1}\equiv h_{c}^{2}/h^{2}$
, where
![]() $h_{c}\equiv \sqrt{T/\unicode[STIX]{x1D70C}g}$
is the capillary length, which is approximately 2 mm in clean water at room temperature and pressure.
$h_{c}\equiv \sqrt{T/\unicode[STIX]{x1D70C}g}$
is the capillary length, which is approximately 2 mm in clean water at room temperature and pressure.
2.2 Key results when
 $Bo^{-1}=0$
and
$Bo^{-1}=0$
and
 $t\ll 1$
$t\ll 1$
Before we study IBVP, we briefly summarise some key results presented in Part 3 concerning the small-time asymptotic solution of IBVP in the absence of surface tension (
![]() $Bo^{-1}=0$
), and refer the interested reader to that paper for a more careful and detailed discussion.
$Bo^{-1}=0$
), and refer the interested reader to that paper for a more careful and detailed discussion.
The most important feature of the solution when
![]() $t\ll 1$
is that its asymptotic structure has both an inner and an outer region.
$t\ll 1$
is that its asymptotic structure has both an inner and an outer region.
2.2.1 Outer solution,
 $x=O(1)$
,
$x=O(1)$
,
 $y=O(1)$
,
$y=O(1)$
,
 $\unicode[STIX]{x1D719}=O(t)$
,
$\unicode[STIX]{x1D719}=O(t)$
,
 $\unicode[STIX]{x1D702}=O(t^{2})$
$\unicode[STIX]{x1D702}=O(t^{2})$
In the outer region, where the leading-order problem is set in the fixed, semi-infinite polygon initially occupied by the fluid with
![]() $x$
,
$x$
,
![]() $y=O(1)$
, we find that
$y=O(1)$
, we find that
as
![]() $t\rightarrow 0$
. Because of the simple geometry of the domain of solution, the
$t\rightarrow 0$
. Because of the simple geometry of the domain of solution, the
![]() $O(1)$
functions
$O(1)$
functions
![]() $\bar{\unicode[STIX]{x1D719}}$
and
$\bar{\unicode[STIX]{x1D719}}$
and
![]() $\bar{\unicode[STIX]{x1D702}}$
can be determined by conformal mapping. As
$\bar{\unicode[STIX]{x1D702}}$
can be determined by conformal mapping. As
![]() $r\equiv \sqrt{x^{2}+y^{2}}\rightarrow 0$
, we find that
$r\equiv \sqrt{x^{2}+y^{2}}\rightarrow 0$
, we find that
where
![]() $A_{0}(\unicode[STIX]{x1D6FC})$
is known and positive, as reported in Part 3. This solution becomes singular and non-uniform as
$A_{0}(\unicode[STIX]{x1D6FC})$
is known and positive, as reported in Part 3. This solution becomes singular and non-uniform as
![]() $r\rightarrow 0$
, since
$r\rightarrow 0$
, since
![]() $\unicode[STIX]{x1D6FC}>\unicode[STIX]{x03C0}/2$
means that
$\unicode[STIX]{x1D6FC}>\unicode[STIX]{x03C0}/2$
means that
![]() $\bar{\unicode[STIX]{x1D702}}\rightarrow \infty$
, which requires the introduction of an inner region.
$\bar{\unicode[STIX]{x1D702}}\rightarrow \infty$
, which requires the introduction of an inner region.
2.2.2 Inner solution,
 $x=O(t^{\unicode[STIX]{x1D6FE}})$
,
$x=O(t^{\unicode[STIX]{x1D6FE}})$
,
 $y=O(t^{\unicode[STIX]{x1D6FE}})$
,
$y=O(t^{\unicode[STIX]{x1D6FE}})$
,
 $\unicode[STIX]{x1D719}=O(t^{2\unicode[STIX]{x1D6FE}-1})$
,
$\unicode[STIX]{x1D719}=O(t^{2\unicode[STIX]{x1D6FE}-1})$
,
 $\unicode[STIX]{x1D702}=O(t^{\unicode[STIX]{x1D6FE}})$
$\unicode[STIX]{x1D702}=O(t^{\unicode[STIX]{x1D6FE}})$
In the inner region, close to the contact line, we define scaled variables using
with hatted variables of
![]() $O(1)$
as
$O(1)$
as
![]() $t\rightarrow 0$
,
$t\rightarrow 0$
,
![]() $l\equiv (A_{0}(\unicode[STIX]{x1D6FC})\unicode[STIX]{x1D70E}\sin \unicode[STIX]{x1D6FC})^{\unicode[STIX]{x1D6FE}/2}$
and
$l\equiv (A_{0}(\unicode[STIX]{x1D6FC})\unicode[STIX]{x1D70E}\sin \unicode[STIX]{x1D6FC})^{\unicode[STIX]{x1D6FE}/2}$
and
![]() $\unicode[STIX]{x1D6FE}\equiv 1/(1-\unicode[STIX]{x03C0}/4\unicode[STIX]{x1D6FC})$
(
$\unicode[STIX]{x1D6FE}\equiv 1/(1-\unicode[STIX]{x03C0}/4\unicode[STIX]{x1D6FC})$
(
![]() $4/3<\unicode[STIX]{x1D6FE}<2$
). At leading order, we obtain a nonlinear boundary value problem that is independent of
$4/3<\unicode[STIX]{x1D6FE}<2$
). At leading order, we obtain a nonlinear boundary value problem that is independent of
![]() $\unicode[STIX]{x1D70E}$
, and depends parametrically on
$\unicode[STIX]{x1D70E}$
, and depends parametrically on
![]() $\unicode[STIX]{x1D6FC}$
alone. Note that the dependence of the solution on the dimensionless acceleration,
$\unicode[STIX]{x1D6FC}$
alone. Note that the dependence of the solution on the dimensionless acceleration,
![]() $\unicode[STIX]{x1D70E}$
, has been scaled out of the problem using
$\unicode[STIX]{x1D70E}$
, has been scaled out of the problem using
![]() $l$
, which shows that the applied acceleration controls the length and time scales, but not the functional form, of the leading-order flow. In Part 3 we were able to solve the leading-order asymptotic problem numerically for
$l$
, which shows that the applied acceleration controls the length and time scales, but not the functional form, of the leading-order flow. In Part 3 we were able to solve the leading-order asymptotic problem numerically for
![]() $\unicode[STIX]{x03C0}/2<\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D6FC}_{c}$
, with
$\unicode[STIX]{x03C0}/2<\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D6FC}_{c}$
, with
![]() $\unicode[STIX]{x1D6FC}_{c}\approx 1.791\approx 102.6^{\circ }$
. Some representative solutions are shown here in figure 2. As
$\unicode[STIX]{x1D6FC}_{c}\approx 1.791\approx 102.6^{\circ }$
. Some representative solutions are shown here in figure 2. As
![]() $\unicode[STIX]{x1D6FC}$
approaches
$\unicode[STIX]{x1D6FC}$
approaches
![]() $\unicode[STIX]{x1D6FC}_{c}$
, the free surface develops a small region of high curvature, which becomes a
$\unicode[STIX]{x1D6FC}_{c}$
, the free surface develops a small region of high curvature, which becomes a
![]() $120^{\circ }$
corner when
$120^{\circ }$
corner when
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{c}$
. For
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{c}$
. For
![]() $\unicode[STIX]{x1D6FC}>\unicode[STIX]{x1D6FC}_{c}$
, we were unable to find a numerical solution and hypothesised that no solution exists for any
$\unicode[STIX]{x1D6FC}>\unicode[STIX]{x1D6FC}_{c}$
, we were unable to find a numerical solution and hypothesised that no solution exists for any
![]() $t>0$
in this case.
$t>0$
in this case.
Note also that, by constructing a local asymptotic solution in the absence of surface tension (in which case (2.6) is no longer imposed), the contact angle can be shown to be
![]() $\unicode[STIX]{x03C0}/2$
. However, the free surface is highly oscillatory close to the contact line with decreasing amplitude and increasing frequency, such that, although the slope is bounded at the contact line, the curvature is not (see Part 3, appendix C, figure C.1). These local singularities in the free surface curvature (at the contact line for all
$\unicode[STIX]{x03C0}/2$
. However, the free surface is highly oscillatory close to the contact line with decreasing amplitude and increasing frequency, such that, although the slope is bounded at the contact line, the curvature is not (see Part 3, appendix C, figure C.1). These local singularities in the free surface curvature (at the contact line for all
![]() $\unicode[STIX]{x1D6FC}>\unicode[STIX]{x03C0}/2$
and also at an interior free surface point when
$\unicode[STIX]{x1D6FC}>\unicode[STIX]{x03C0}/2$
and also at an interior free surface point when
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{c}$
) suggest that it makes sense to introduce surface tension into the problem and study IBVP with
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{c}$
) suggest that it makes sense to introduce surface tension into the problem and study IBVP with
![]() $Bo^{-1}>0$
.
$Bo^{-1}>0$
.

Figure 2. The free surface in the inner region in the absence of surface tension (
![]() $Bo^{-1}=0$
). The solutions shown have
$Bo^{-1}=0$
). The solutions shown have
![]() $\unicode[STIX]{x1D6FC}=1.6$
, 1.65, 1.7, 1.75, 1.76, 1.77, 1.78 and 1.791.
$\unicode[STIX]{x1D6FC}=1.6$
, 1.65, 1.7, 1.75, 1.76, 1.77, 1.78 and 1.791.
3 Asymptotic solution for
 $Bo^{-1}\ll 1$
$Bo^{-1}\ll 1$
When
![]() $Bo^{-1}\ll 1$
(capillary length much smaller than initial fluid depth) it is possible to determine the asymptotic solution structure of the correction terms due to surface tension in the outer region. However, the part of the solution structure in which we are mainly interested is the inner region that lies close to the contact line, which we described above, where all the interesting fluid mechanics occurs (including all of the capillary ripples and the possibility of pinch-off, which we will discuss below). We therefore focus our attention on how surface tension affects this region.
$Bo^{-1}\ll 1$
(capillary length much smaller than initial fluid depth) it is possible to determine the asymptotic solution structure of the correction terms due to surface tension in the outer region. However, the part of the solution structure in which we are mainly interested is the inner region that lies close to the contact line, which we described above, where all the interesting fluid mechanics occurs (including all of the capillary ripples and the possibility of pinch-off, which we will discuss below). We therefore focus our attention on how surface tension affects this region.
For
![]() $Bo^{-1}\ll 1$
, the outer solution discussed in § 2.2.1 remains the leading-order solution for
$Bo^{-1}\ll 1$
, the outer solution discussed in § 2.2.1 remains the leading-order solution for
![]() $x$
,
$x$
,
![]() $y=O(1)$
. When we now consider how this solution behaves as
$y=O(1)$
. When we now consider how this solution behaves as
![]() $r\rightarrow 0$
, given by (2.10), in particular the orders of magnitude of the terms in the Bernoulli equation, (2.5), we find that the dominant terms on the left-hand side are of
$r\rightarrow 0$
, given by (2.10), in particular the orders of magnitude of the terms in the Bernoulli equation, (2.5), we find that the dominant terms on the left-hand side are of
![]() $O(t^{2\unicode[STIX]{x1D6FE}-2})$
, and the surface tension term on the right-hand side is of
$O(t^{2\unicode[STIX]{x1D6FE}-2})$
, and the surface tension term on the right-hand side is of
![]() $O(Bo^{-1}t^{-\unicode[STIX]{x1D6FE}})$
. This suggests that, as
$O(Bo^{-1}t^{-\unicode[STIX]{x1D6FE}})$
. This suggests that, as
![]() $t\rightarrow 0$
, the outer solution becomes non-uniform when
$t\rightarrow 0$
, the outer solution becomes non-uniform when
![]() $t=O(Bo^{-1/(3\unicode[STIX]{x1D6FE}-2)})$
and
$t=O(Bo^{-1/(3\unicode[STIX]{x1D6FE}-2)})$
and
![]() $x$
,
$x$
,
![]() $y$
,
$y$
,
![]() $\unicode[STIX]{x1D702}=O(Bo^{-\unicode[STIX]{x1D6FE}/(3\unicode[STIX]{x1D6FE}-2)})$
. Note that
$\unicode[STIX]{x1D702}=O(Bo^{-\unicode[STIX]{x1D6FE}/(3\unicode[STIX]{x1D6FE}-2)})$
. Note that
![]() $-1/2<-(1/(3\unicode[STIX]{x1D6FE}-2))<-1/4$
and
$-1/2<-(1/(3\unicode[STIX]{x1D6FE}-2))<-1/4$
and
![]() $-2/3<-(\unicode[STIX]{x1D6FE}/(3\unicode[STIX]{x1D6FE}-2))<-1/2$
.
$-2/3<-(\unicode[STIX]{x1D6FE}/(3\unicode[STIX]{x1D6FE}-2))<-1/2$
.
We therefore define new dimensionless variables in an inner region, close to the contact line, using
with all tilded variables of
![]() $O(1)$
as
$O(1)$
as
![]() $Bo^{-1}\rightarrow 0$
. After rewriting IBVP in terms of these new variables we obtain, at leading order,
$Bo^{-1}\rightarrow 0$
. After rewriting IBVP in terms of these new variables we obtain, at leading order,
where
![]() $(\tilde{r},\unicode[STIX]{x1D703})$
are polar coordinates centred at the origin (the initial position of the contact line), with
$(\tilde{r},\unicode[STIX]{x1D703})$
are polar coordinates centred at the origin (the initial position of the contact line), with
![]() $\unicode[STIX]{x1D703}=0$
on the inclined plate.
$\unicode[STIX]{x1D703}=0$
on the inclined plate.
We will refer to the initial boundary value problem given by (3.3)–(3.10) as IP (inner problem). For the most part, IP is a standard free surface flow problem, with the usual kinematic and Bernoulli conditions, a constant contact angle condition at the contact line,
![]() $(\tilde{x}_{c}(\tilde{t}),{\tilde{y}}_{c}(\tilde{t}))$
and the fluid initially at rest with the free surface horizontal. However, it is unusual in that it is forced at infinity by an unsteady flow that becomes stronger as
$(\tilde{x}_{c}(\tilde{t}),{\tilde{y}}_{c}(\tilde{t}))$
and the fluid initially at rest with the free surface horizontal. However, it is unusual in that it is forced at infinity by an unsteady flow that becomes stronger as
![]() $\tilde{t}$
increases, given by (3.9) and (3.10), which comes from matching to the outer solution, (2.10), which is singular as the inner region is approached, and dominates the effect of both gravity and the motion of the plate at leading order (the right-hand side of (3.4) is zero and there are no terms due to the moving frame of reference in (3.5)). As scaled, the driving acceleration only appears in (3.6) where it quantifies the importance of surface tension forces through the coefficient
$\tilde{t}$
increases, given by (3.9) and (3.10), which comes from matching to the outer solution, (2.10), which is singular as the inner region is approached, and dominates the effect of both gravity and the motion of the plate at leading order (the right-hand side of (3.4) is zero and there are no terms due to the moving frame of reference in (3.5)). As scaled, the driving acceleration only appears in (3.6) where it quantifies the importance of surface tension forces through the coefficient
![]() $l^{-3}$
, which is a decreasing function of
$l^{-3}$
, which is a decreasing function of
![]() $\unicode[STIX]{x1D70E}$
. Note also that only the first term on the right-hand side of (3.9) is given by matching at leading order. The other term appears at higher order, but can be determined by seeking an asymptotic expansion valid for
$\unicode[STIX]{x1D70E}$
. Note also that only the first term on the right-hand side of (3.9) is given by matching at leading order. The other term appears at higher order, but can be determined by seeking an asymptotic expansion valid for
![]() $\tilde{r}\gg 1$
. This term is included to improve the accuracy of our numerical solutions, which will be discussed in § 3.2.
$\tilde{r}\gg 1$
. This term is included to improve the accuracy of our numerical solutions, which will be discussed in § 3.2.
A key point to note is that as
![]() $\tilde{t}\rightarrow \infty$
, the inner solution of the problem with
$\tilde{t}\rightarrow \infty$
, the inner solution of the problem with
![]() $Bo^{-1}=0$
, discussed in § 2.2.2, is the large-time solution of IP. Thus, when
$Bo^{-1}=0$
, discussed in § 2.2.2, is the large-time solution of IP. Thus, when
![]() $\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D6FC}_{c}$
, we know the large-time asymptotic solution, which we will see below does give the large-time structure of the numerical solutions of IP that we calculate. However, for
$\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D6FC}_{c}$
, we know the large-time asymptotic solution, which we will see below does give the large-time structure of the numerical solutions of IP that we calculate. However, for
![]() $\unicode[STIX]{x1D6FC}>\unicode[STIX]{x1D6FC}_{c}$
, as discussed above, this means that there is strong numerical evidence that no large-time solution of IP exists. As we shall see below, the solution does indeed fail to exist beyond a finite time at which the free surface self-intersects (pinch-off). A real fluid flow of this type would continue after this topological change, but the mathematical problem that models the system after the pinch-off time would need to be reformulated to take into account the trapped air pocket.
$\unicode[STIX]{x1D6FC}>\unicode[STIX]{x1D6FC}_{c}$
, as discussed above, this means that there is strong numerical evidence that no large-time solution of IP exists. As we shall see below, the solution does indeed fail to exist beyond a finite time at which the free surface self-intersects (pinch-off). A real fluid flow of this type would continue after this topological change, but the mathematical problem that models the system after the pinch-off time would need to be reformulated to take into account the trapped air pocket.
3.1 Small-time solution of the unsteady inner problem
The interesting dynamics of the free surface in the solution of IP occurs when
![]() $\tilde{t}=O(1)$
, and it would not usually be worth presenting the details of the solution when
$\tilde{t}=O(1)$
, and it would not usually be worth presenting the details of the solution when
![]() $\tilde{t}$
is small. However, one of the key questions that we want to investigate is whether, when
$\tilde{t}$
is small. However, one of the key questions that we want to investigate is whether, when
![]() $\unicode[STIX]{x1D6FC}>\unicode[STIX]{x1D6FC}_{c}$
, the inclusion of surface tension allows a solution to exist, at least for some finite time. We can investigate this by constructing the formal asymptotic solution of IP when
$\unicode[STIX]{x1D6FC}>\unicode[STIX]{x1D6FC}_{c}$
, the inclusion of surface tension allows a solution to exist, at least for some finite time. We can investigate this by constructing the formal asymptotic solution of IP when
![]() $\tilde{t}\ll 1$
. The obvious natural scaling, driven by the far-field conditions, equations (3.9) and (3.10), has
$\tilde{t}\ll 1$
. The obvious natural scaling, driven by the far-field conditions, equations (3.9) and (3.10), has
![]() $\tilde{\unicode[STIX]{x1D719}}=O(\tilde{t})$
and
$\tilde{\unicode[STIX]{x1D719}}=O(\tilde{t})$
and
![]() $\tilde{\unicode[STIX]{x1D702}}=O(\tilde{t}^{2})$
as
$\tilde{\unicode[STIX]{x1D702}}=O(\tilde{t}^{2})$
as
![]() $\tilde{t}\rightarrow 0$
. However, at leading order, this simply reproduces the far-field solution, with the surface tension term in the Bernoulli condition not active at leading order. In the absence of surface tension, we know that there is an inner region where
$\tilde{t}\rightarrow 0$
. However, at leading order, this simply reproduces the far-field solution, with the surface tension term in the Bernoulli condition not active at leading order. In the absence of surface tension, we know that there is an inner region where
![]() $(\tilde{x},{\tilde{y}})=O(\tilde{t}^{\unicode[STIX]{x1D6FE}})$
as
$(\tilde{x},{\tilde{y}})=O(\tilde{t}^{\unicode[STIX]{x1D6FE}})$
as
![]() $\tilde{t}\rightarrow 0$
. However, with surface tension present, the curvature term becomes comparable to the leading-order terms when
$\tilde{t}\rightarrow 0$
. However, with surface tension present, the curvature term becomes comparable to the leading-order terms when
![]() $(\tilde{x},{\tilde{y}})=O(\tilde{t}^{2/3})$
. Since
$(\tilde{x},{\tilde{y}})=O(\tilde{t}^{2/3})$
. Since
![]() $\unicode[STIX]{x1D6FE}>2/3$
, it is this second length scale that dominates and hence surface tension suppresses the emergence of the structures that we studied in Part 3 and allows the solution to exist at small times. The emergence of a solution with lengths scaling like
$\unicode[STIX]{x1D6FE}>2/3$
, it is this second length scale that dominates and hence surface tension suppresses the emergence of the structures that we studied in Part 3 and allows the solution to exist at small times. The emergence of a solution with lengths scaling like
![]() $\tilde{t}^{2/3}$
as
$\tilde{t}^{2/3}$
as
![]() $\tilde{t}\rightarrow 0$
is typical for problems where the motion is dominated by surface tension forces and inertia (for example Keller & Miksis Reference Keller and Miksis1983; Billingham Reference Billingham2006).
$\tilde{t}\rightarrow 0$
is typical for problems where the motion is dominated by surface tension forces and inertia (for example Keller & Miksis Reference Keller and Miksis1983; Billingham Reference Billingham2006).
In order to formulate the asymptotic structure of the solution of IP as
![]() $\tilde{t}\rightarrow 0$
, we define scaled variables
$\tilde{t}\rightarrow 0$
, we define scaled variables
with
![]() $X$
,
$X$
,
![]() $Y$
,
$Y$
,
![]() $Y_{s}$
,
$Y_{s}$
,
![]() $\unicode[STIX]{x1D6F7}=O(1)$
as
$\unicode[STIX]{x1D6F7}=O(1)$
as
![]() $\tilde{t}\rightarrow 0$
. At leading order we obtain a boundary value problem that depends only on
$\tilde{t}\rightarrow 0$
. At leading order we obtain a boundary value problem that depends only on
![]() $\unicode[STIX]{x1D6FC}$
, namely
$\unicode[STIX]{x1D6FC}$
, namely
Note that, unlike the small-time problem in the absence of surface tension, this boundary value problem is linear, and the domain of solution is a wedge. We also note that
We have solved (3.12) to (3.18) using a boundary integral method, with linear elements, integrating over a domain bounded by an arc of a large circle. We used a similar numerical method to solve the nonlinear problem in appendix B of Part 3. The free surface,
![]() $Y_{s}(X)$
, and potential on the free surface,
$Y_{s}(X)$
, and potential on the free surface,
![]() $\unicode[STIX]{x1D6F7}(X,Y_{s}(X))$
, are shown in figures 3 and 4. The amplitude of both these functions increases as the angle of the plate,
$\unicode[STIX]{x1D6F7}(X,Y_{s}(X))$
, are shown in figures 3 and 4. The amplitude of both these functions increases as the angle of the plate,
![]() $\unicode[STIX]{x1D6FC}$
, increases, but it is noticeable that the position of the contact line,
$\unicode[STIX]{x1D6FC}$
, increases, but it is noticeable that the position of the contact line,
![]() $Y_{s}(0)$
, remains close to 0.5, independent of
$Y_{s}(0)$
, remains close to 0.5, independent of
![]() $\unicode[STIX]{x1D6FC}$
.
$\unicode[STIX]{x1D6FC}$
.

Figure 3. The position of the free surface at small times. The larger the angle
![]() $\unicode[STIX]{x1D6FC}$
, the larger the deformation of the free surface.
$\unicode[STIX]{x1D6FC}$
, the larger the deformation of the free surface.

Figure 4. The potential on the free surface at small times. The larger the angle
![]() $\unicode[STIX]{x1D6FC}$
, the larger the size of this potential.
$\unicode[STIX]{x1D6FC}$
, the larger the size of this potential.
We have been able to determine numerically the small-time asymptotic solution for
![]() $\unicode[STIX]{x1D6FC}>\unicode[STIX]{x03C0}/2$
, which provides strong evidence that, in the presence of surface tension, a solution exists for some time interval, even if
$\unicode[STIX]{x1D6FC}>\unicode[STIX]{x03C0}/2$
, which provides strong evidence that, in the presence of surface tension, a solution exists for some time interval, even if
![]() $\unicode[STIX]{x1D6FC}>\unicode[STIX]{x1D6FC}_{c}$
. This strongly suggests that taking
$\unicode[STIX]{x1D6FC}>\unicode[STIX]{x1D6FC}_{c}$
. This strongly suggests that taking
![]() $Bo^{-1}=0$
is a singular perturbation. We now need to determine what happens when
$Bo^{-1}=0$
is a singular perturbation. We now need to determine what happens when
![]() $\tilde{t}=O(1)$
by solving IP numerically.
$\tilde{t}=O(1)$
by solving IP numerically.
3.2 Numerical solution of the unsteady inner problem
We solve IP numerically, using a boundary integral method to solve Laplace’s equation at each time step. The key points of our numerical method are:
-
(i) We use an iterative method to solve the boundary integral equation for the streamfunction,
 $\tilde{\unicode[STIX]{x1D713}}$
, which can easily be related to the potential
$\tilde{\unicode[STIX]{x1D713}}$
, which can easily be related to the potential
 $\tilde{\unicode[STIX]{x1D719}}$
.
$\tilde{\unicode[STIX]{x1D719}}$
. -
(ii) We close the domain of solution using an arc of a large circle, where we impose the equivalent of the boundary condition (3.9) on
 $\tilde{\unicode[STIX]{x1D713}}$
.
$\tilde{\unicode[STIX]{x1D713}}$
. -
(iii) We use straight line elements with
 $\tilde{\unicode[STIX]{x1D713}}$
varying linearly on each.
$\tilde{\unicode[STIX]{x1D713}}$
varying linearly on each. -
(iv) The integrals along each free surface element are evaluated analytically. This is a better option than Gaussian quadrature for this particular problem, since boundary elements can become close to each other prior to the free surface pinching off, which makes it important to deal accurately with the logarithmic singularities on close, but non-consecutive, elements. The integrals on the elements on the large circle are calculated using four-point Gaussian quadrature.
-
(v) Since we know that the solution develops on a length scale of
 $O(l^{-1}\tilde{t}^{2/3})$
when
$O(l^{-1}\tilde{t}^{2/3})$
when
 $\tilde{t}\ll 1$
and of
$\tilde{t}\ll 1$
and of
 $O(\tilde{t}^{\unicode[STIX]{x1D6FE}})$
when
$O(\tilde{t}^{\unicode[STIX]{x1D6FE}})$
when
 $\tilde{t}\gg 1$
, we scale lengths with
$\tilde{t}\gg 1$
, we scale lengths with
 $l^{-1}k\tilde{t}^{2/3}+L\tilde{t}^{\unicode[STIX]{x1D6FE}}$
. By judicious choice of the constants
$l^{-1}k\tilde{t}^{2/3}+L\tilde{t}^{\unicode[STIX]{x1D6FE}}$
. By judicious choice of the constants
 $k$
and
$k$
and
 $L$
, we can keep the active part of the solution within the finite numerical domain.
$L$
, we can keep the active part of the solution within the finite numerical domain. -
(vi) Time stepping is fully implicit Euler. Implicit time stepping is the only way to deal with the contact angle boundary condition, equation (2.6).
-
(vii) The tangential velocities of the discrete points that determine the piecewise linear free boundary are solved for implicitly as part of the quasi-Newton iteration, and are constrained to preserve the ratio of successive element lengths, thereby preventing unwanted shrinkage or stretching of boundary elements.
-
(viii) We use a quasi-Newton method to solve the resulting system of nonlinear equations at each time step.
-
(ix) The free surface is adaptively regridded in order to concentrate points in regions of high curvature. Specifically, we fit quintic splines to the free surface, so that the curvature is fitted by a cubic spline, and regrid based on this representation of all surface variables. This is done whenever the local ratio of the radius of curvature to grid spacing passes over a threshold value.
-
(x) No smoothing is applied to the solution, and a very weak, high-frequency instability can cause the solution to terminate just before pinch-off. The instability manifests itself as a sawtooth disturbance to the curvature of the free surface and is probably related to similar instabilities observed when boundary integral methods are used in related flows (for example Dold Reference Dold1992; Im & Billingham Reference Im and Billingham2016).
We computed the time,
![]() $\tilde{t}=\unicode[STIX]{x1D70F}_{c}$
, of pinch-off by detecting when non-adjacent parts of the interface become close, monitoring their separation as a function of time and extrapolating. In order to avoid the weak instability discussed above, we terminated the simulation when this distance had halved. A typical plot of this distance as a function of time, along with the extrapolation used is shown in figure 5.
$\tilde{t}=\unicode[STIX]{x1D70F}_{c}$
, of pinch-off by detecting when non-adjacent parts of the interface become close, monitoring their separation as a function of time and extrapolating. In order to avoid the weak instability discussed above, we terminated the simulation when this distance had halved. A typical plot of this distance as a function of time, along with the extrapolation used is shown in figure 5.

Figure 5. The shortest distance between non-adjacent parts of the free surface as a function of time when
![]() $\unicode[STIX]{x1D70E}=1$
and
$\unicode[STIX]{x1D70E}=1$
and
![]() $\unicode[STIX]{x1D6FC}=2.3$
. In this case,
$\unicode[STIX]{x1D6FC}=2.3$
. In this case,
![]() $\unicode[STIX]{x1D70F}_{c}\approx 4.69$
.
$\unicode[STIX]{x1D70F}_{c}\approx 4.69$
.
3.3 Numerical solutions
We begin by comparing our numerical solutions to the small-time asymptotic solution that we obtained in § 3.1. The numerical solution when
![]() $\tilde{t}$
is small is in good agreement with the asymptotic solution. The position of the contact line and the potential at the contact line for both the full numerical and small-time solutions are shown in figure 6 for the typical case
$\tilde{t}$
is small is in good agreement with the asymptotic solution. The position of the contact line and the potential at the contact line for both the full numerical and small-time solutions are shown in figure 6 for the typical case
![]() $\unicode[STIX]{x1D6FC}=2.3$
.
$\unicode[STIX]{x1D6FC}=2.3$
.

Figure 6. A comparison of the numerical and asymptotic solutions with
![]() $\unicode[STIX]{x1D6FC}=2.3$
.
$\unicode[STIX]{x1D6FC}=2.3$
.
Figures 7–9 show the evolution of the free surface for various
![]() $\unicode[STIX]{x1D6FC}$
with
$\unicode[STIX]{x1D6FC}$
with
![]() $\unicode[STIX]{x03C0}/2<\unicode[STIX]{x1D6FC}\leqslant 1.8$
. In each case, we drew on the numerical results in Part 3 to ensure that the resolution of the free surface was such that the critical value of
$\unicode[STIX]{x03C0}/2<\unicode[STIX]{x1D6FC}\leqslant 1.8$
. In each case, we drew on the numerical results in Part 3 to ensure that the resolution of the free surface was such that the critical value of
![]() $\unicode[STIX]{x1D6FC}$
, the inclination of the plate to the horizontal, is well resolved at
$\unicode[STIX]{x1D6FC}$
, the inclination of the plate to the horizontal, is well resolved at
![]() $\unicode[STIX]{x1D6FC}_{c}\approx 1.791$
. Recall that, in the absence of surface tension, there is strong evidence that no solution exists for
$\unicode[STIX]{x1D6FC}_{c}\approx 1.791$
. Recall that, in the absence of surface tension, there is strong evidence that no solution exists for
![]() $\unicode[STIX]{x1D6FC}>\unicode[STIX]{x1D6FC}_{c}$
. On this scale, each of the solutions in figures 7–9 looks qualitatively very similar. Small amplitude capillary ripples appear on the surface ahead of a local maximum in height, which we will refer to as the wavecrest. These ripples are an unsteady analogue of the parasitic capillary ripples that appear ahead of the wavecrest in steady capillary/gravity waves (see, for example, Longuet-Higgins (Reference Longuet-Higgins1997), Ceniceros & Hou (Reference Ceniceros and Hou1999) for other approaches to studying unsteady capillary ripples). At the smallest value of
$\unicode[STIX]{x1D6FC}>\unicode[STIX]{x1D6FC}_{c}$
. On this scale, each of the solutions in figures 7–9 looks qualitatively very similar. Small amplitude capillary ripples appear on the surface ahead of a local maximum in height, which we will refer to as the wavecrest. These ripples are an unsteady analogue of the parasitic capillary ripples that appear ahead of the wavecrest in steady capillary/gravity waves (see, for example, Longuet-Higgins (Reference Longuet-Higgins1997), Ceniceros & Hou (Reference Ceniceros and Hou1999) for other approaches to studying unsteady capillary ripples). At the smallest value of
![]() $\unicode[STIX]{x1D6FC}$
shown here (
$\unicode[STIX]{x1D6FC}$
shown here (
![]() $\unicode[STIX]{x1D6FC}=1.75$
), these ripples can be seen to decay as the free surface rises up the plate, and the solution asymptotes to the large-time solution that exists in the absence of surface tension, with a capillary boundary layer near the plate that allows the contact angle to adjust to
$\unicode[STIX]{x1D6FC}=1.75$
), these ripples can be seen to decay as the free surface rises up the plate, and the solution asymptotes to the large-time solution that exists in the absence of surface tension, with a capillary boundary layer near the plate that allows the contact angle to adjust to
![]() $\unicode[STIX]{x1D6FC}$
instead of the natural value,
$\unicode[STIX]{x1D6FC}$
instead of the natural value,
![]() $\unicode[STIX]{x03C0}/2$
, associated with the large-time solution (this is very hard to see in the figures, since we have plotted on a scale that emphasises the behaviour of the ripples, but the capillary boundary layer is there). As
$\unicode[STIX]{x03C0}/2$
, associated with the large-time solution (this is very hard to see in the figures, since we have plotted on a scale that emphasises the behaviour of the ripples, but the capillary boundary layer is there). As
![]() $\unicode[STIX]{x1D6FC}$
increases, these ripples can be seen to persist. Figure 10 shows a close up of the ripples just ahead of the wavecrest for four values of
$\unicode[STIX]{x1D6FC}$
increases, these ripples can be seen to persist. Figure 10 shows a close up of the ripples just ahead of the wavecrest for four values of
![]() $\unicode[STIX]{x1D6FC}$
when
$\unicode[STIX]{x1D6FC}$
when
![]() $\tilde{t}=9$
. The ripples when
$\tilde{t}=9$
. The ripples when
![]() $\unicode[STIX]{x1D6FC}=1.78$
are significantly weaker than those for the other three values shown, and decay as
$\unicode[STIX]{x1D6FC}=1.78$
are significantly weaker than those for the other three values shown, and decay as
![]() $\tilde{t}\rightarrow \infty$
, leaving only the large-time solution. In the other three cases, the ripples are very similar in form, amplitude and frequency, with decreasing amplitude and increasing frequency down the wavecrest. However, for
$\tilde{t}\rightarrow \infty$
, leaving only the large-time solution. In the other three cases, the ripples are very similar in form, amplitude and frequency, with decreasing amplitude and increasing frequency down the wavecrest. However, for
![]() $\unicode[STIX]{x1D6FC}=1.79<\unicode[STIX]{x1D6FC}_{c}$
, the ripples decay as
$\unicode[STIX]{x1D6FC}=1.79<\unicode[STIX]{x1D6FC}_{c}$
, the ripples decay as
![]() $\tilde{t}\rightarrow \infty$
, whilst for the other two cases, pinch-off occurs at finite
$\tilde{t}\rightarrow \infty$
, whilst for the other two cases, pinch-off occurs at finite
![]() $\tilde{t}$
, as shown in figure 11. These are the final free surface profiles computed before the solution became too close to pinch-off, as calculated using the extrapolation procedure described above. In all cases, the shape of the free surface close to pinch-off is qualitatively very similar to the most extreme nonlinear capillary waves discovered by Crapper (Reference Crapper1957). Note also the slight irregularity of the nonlinear capillary waves shown in figure 10. Although a specific cause of this irregularity is not immediately obvious, this is a well-resolved feature of the flow, and not a numerical artefact, and is probably caused by the nonlinear interaction between the peaks and troughs of the wave, coupled with the unsteady, asymmetric nature of the flow. It is within this region of nonlinear interaction that pinch-off occurs. However, as discussed below, the occurrence of free surface pinch-off appears to be a global feature of the flow, controlled by the plate angle
$\tilde{t}$
, as shown in figure 11. These are the final free surface profiles computed before the solution became too close to pinch-off, as calculated using the extrapolation procedure described above. In all cases, the shape of the free surface close to pinch-off is qualitatively very similar to the most extreme nonlinear capillary waves discovered by Crapper (Reference Crapper1957). Note also the slight irregularity of the nonlinear capillary waves shown in figure 10. Although a specific cause of this irregularity is not immediately obvious, this is a well-resolved feature of the flow, and not a numerical artefact, and is probably caused by the nonlinear interaction between the peaks and troughs of the wave, coupled with the unsteady, asymmetric nature of the flow. It is within this region of nonlinear interaction that pinch-off occurs. However, as discussed below, the occurrence of free surface pinch-off appears to be a global feature of the flow, controlled by the plate angle
![]() $\unicode[STIX]{x1D6FC}$
alone, and not dependent on the local dynamics of the capillary waves.
$\unicode[STIX]{x1D6FC}$
alone, and not dependent on the local dynamics of the capillary waves.

Figure 7. The evolution of the free surface for various
![]() $\unicode[STIX]{x1D6FC}$
, with
$\unicode[STIX]{x1D6FC}$
, with
![]() $\unicode[STIX]{x1D70E}=1$
. In each case, the solution is plotted at intervals of 0.5 time units in
$\unicode[STIX]{x1D70E}=1$
. In each case, the solution is plotted at intervals of 0.5 time units in
![]() $\tilde{t}$
.
$\tilde{t}$
.

Figure 8. The evolution of the free surface for various
![]() $\unicode[STIX]{x1D6FC}$
, with
$\unicode[STIX]{x1D6FC}$
, with
![]() $\unicode[STIX]{x1D70E}=1$
. In each case, the solution is plotted at intervals of 0.5 time units in
$\unicode[STIX]{x1D70E}=1$
. In each case, the solution is plotted at intervals of 0.5 time units in
![]() $\tilde{t}$
.
$\tilde{t}$
.

Figure 9. The evolution of the free surface for various
![]() $\unicode[STIX]{x1D6FC}$
, with
$\unicode[STIX]{x1D6FC}$
, with
![]() $\unicode[STIX]{x1D70E}=1$
. In each case, the solution is plotted at intervals of 0.5 time units in
$\unicode[STIX]{x1D70E}=1$
. In each case, the solution is plotted at intervals of 0.5 time units in
![]() $\tilde{t}$
.
$\tilde{t}$
.

Figure 10. Enlarged view of the parasitic capillary wave on the free surface just ahead of the wavecrest for various
![]() $\unicode[STIX]{x1D6FC}$
with
$\unicode[STIX]{x1D6FC}$
with
![]() $\unicode[STIX]{x1D70E}=1$
when
$\unicode[STIX]{x1D70E}=1$
when
![]() $\tilde{t}=9$
. Note the slight irregularity in the nonlinear capillary waves, probably due to the nonlinear interaction of their peaks and troughs, and their response to the unsteady, asymmetric nature of the flow.
$\tilde{t}=9$
. Note the slight irregularity in the nonlinear capillary waves, probably due to the nonlinear interaction of their peaks and troughs, and their response to the unsteady, asymmetric nature of the flow.
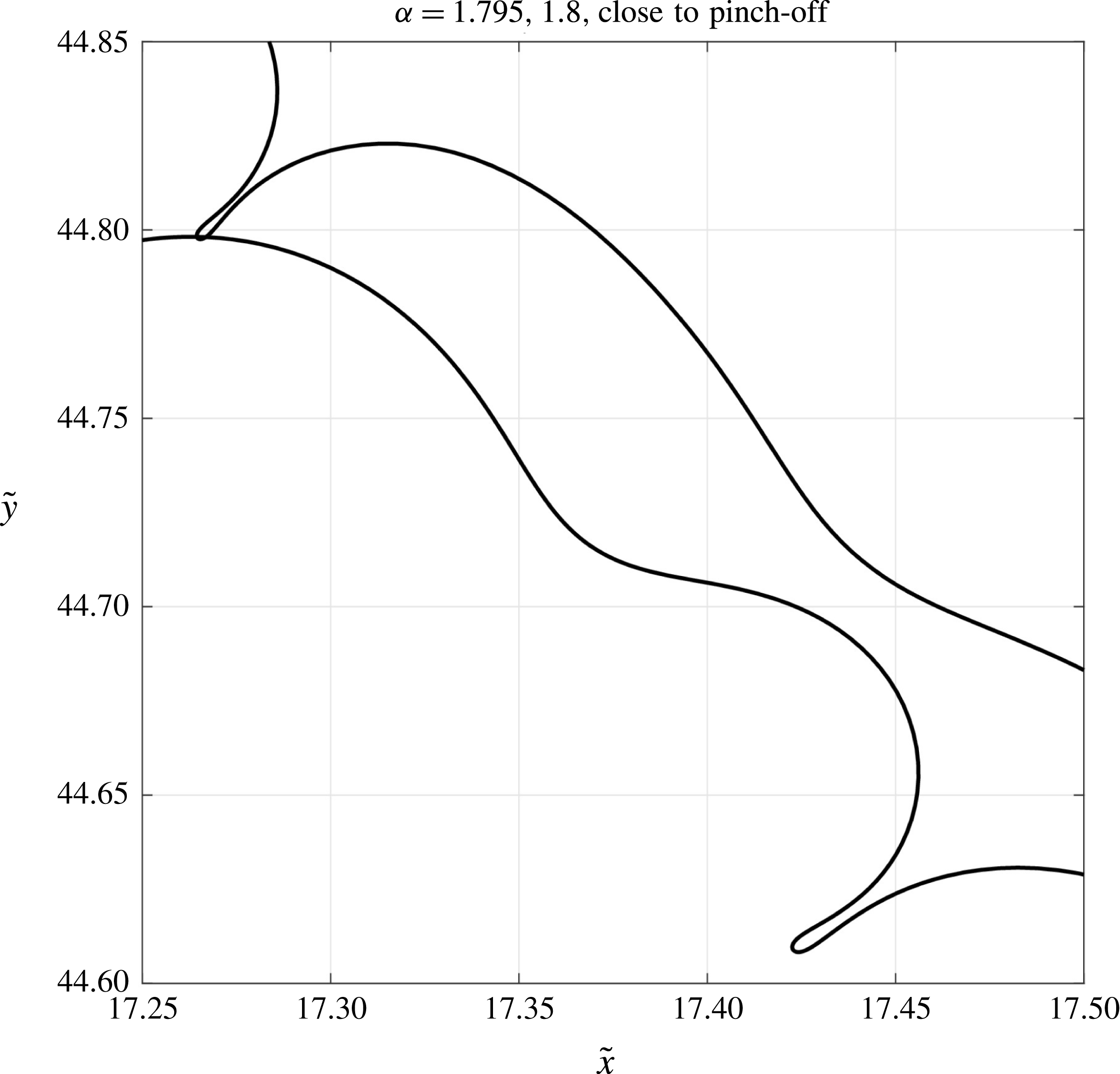
Figure 11. The local free surface just before pinch-off for
![]() $\unicode[STIX]{x1D6FC}=1.795$
and
$\unicode[STIX]{x1D6FC}=1.795$
and
![]() $\unicode[STIX]{x1D6FC}=1.8$
, with
$\unicode[STIX]{x1D6FC}=1.8$
, with
![]() $\unicode[STIX]{x1D70E}=1$
.
$\unicode[STIX]{x1D70E}=1$
.
There is no a priori reason either why the existence of a large-time solution for
![]() $\unicode[STIX]{x1D6FC}<\unicode[STIX]{x1D6FC}_{c}$
should preclude the existence of solutions that pinch-off, given the fact that capillary ripples also form on the free surface in this case, or that the non-existence of a large-time solution when
$\unicode[STIX]{x1D6FC}<\unicode[STIX]{x1D6FC}_{c}$
should preclude the existence of solutions that pinch-off, given the fact that capillary ripples also form on the free surface in this case, or that the non-existence of a large-time solution when
![]() $\unicode[STIX]{x1D6FC}>\unicode[STIX]{x1D6FC}_{c}$
should mean that an unsteady solution with propagating capillary ripples that do not pinch off does not exist. However, we have been unable to find any numerical evidence of either of these phenomena, even when varying the acceleration
$\unicode[STIX]{x1D6FC}>\unicode[STIX]{x1D6FC}_{c}$
should mean that an unsteady solution with propagating capillary ripples that do not pinch off does not exist. However, we have been unable to find any numerical evidence of either of these phenomena, even when varying the acceleration
![]() $\unicode[STIX]{x1D70E}$
to extreme values. This leads us to conjecture that for
$\unicode[STIX]{x1D70E}$
to extreme values. This leads us to conjecture that for
![]() $\unicode[STIX]{x1D6FC}<\unicode[STIX]{x1D6FC}_{c}$
, the solution asymptotes to the large-time solution, with any capillary ripples that form decaying away as
$\unicode[STIX]{x1D6FC}<\unicode[STIX]{x1D6FC}_{c}$
, the solution asymptotes to the large-time solution, with any capillary ripples that form decaying away as
![]() $\tilde{t}\rightarrow \infty$
, and that when
$\tilde{t}\rightarrow \infty$
, and that when
![]() $\unicode[STIX]{x1D6FC}>\unicode[STIX]{x1D6FC}_{c}$
, the capillary ripples ahead of the wavecrest always lead to pinch-off at finite
$\unicode[STIX]{x1D6FC}>\unicode[STIX]{x1D6FC}_{c}$
, the capillary ripples ahead of the wavecrest always lead to pinch-off at finite
![]() $\tilde{t}$
. The growth of the ripples and the subsequent pinch-off is very clear for values of
$\tilde{t}$
. The growth of the ripples and the subsequent pinch-off is very clear for values of
![]() $\unicode[STIX]{x1D6FC}$
somewhat larger than
$\unicode[STIX]{x1D6FC}$
somewhat larger than
![]() $\unicode[STIX]{x1D6FC}_{c}$
, as shown in figures 12 and 13. As
$\unicode[STIX]{x1D6FC}_{c}$
, as shown in figures 12 and 13. As
![]() $\unicode[STIX]{x1D6FC}$
increases towards
$\unicode[STIX]{x1D6FC}$
increases towards
![]() $\unicode[STIX]{x03C0}$
, the free surface moves more rapidly, and pinch-off occurs earlier. The pinch-off time,
$\unicode[STIX]{x03C0}$
, the free surface moves more rapidly, and pinch-off occurs earlier. The pinch-off time,
![]() $\unicode[STIX]{x1D70F}_{c}$
, is plotted in figure 14 as a function of
$\unicode[STIX]{x1D70F}_{c}$
, is plotted in figure 14 as a function of
![]() $\unicode[STIX]{x1D6FC}$
for
$\unicode[STIX]{x1D6FC}$
for
![]() $\unicode[STIX]{x1D70E}=1$
. There is strong numerical evidence that
$\unicode[STIX]{x1D70E}=1$
. There is strong numerical evidence that
![]() $\unicode[STIX]{x1D70F}_{c}\rightarrow \infty$
as
$\unicode[STIX]{x1D70F}_{c}\rightarrow \infty$
as
![]() $\unicode[STIX]{x1D6FC}\rightarrow \unicode[STIX]{x1D6FC}_{c}^{+}$
, and also a suggestion that
$\unicode[STIX]{x1D6FC}\rightarrow \unicode[STIX]{x1D6FC}_{c}^{+}$
, and also a suggestion that
![]() $\unicode[STIX]{x1D70F}_{c}\rightarrow 0$
as
$\unicode[STIX]{x1D70F}_{c}\rightarrow 0$
as
![]() $\unicode[STIX]{x1D6FC}\rightarrow \unicode[STIX]{x03C0}^{-}$
. The latter limit is singular (planing), and would need to be studied separately.
$\unicode[STIX]{x1D6FC}\rightarrow \unicode[STIX]{x03C0}^{-}$
. The latter limit is singular (planing), and would need to be studied separately.

Figure 12. The evolution of the free surface for various
![]() $\unicode[STIX]{x1D6FC}$
, with
$\unicode[STIX]{x1D6FC}$
, with
![]() $\unicode[STIX]{x1D70E}=1$
. In each case, the solution is plotted at intervals of 0.5 time units in
$\unicode[STIX]{x1D70E}=1$
. In each case, the solution is plotted at intervals of 0.5 time units in
![]() $\tilde{t}$
.
$\tilde{t}$
.

Figure 13. The evolution of the free surface for various
![]() $\unicode[STIX]{x1D6FC}$
, with
$\unicode[STIX]{x1D6FC}$
, with
![]() $\unicode[STIX]{x1D70E}=1$
. In each case, the solution is plotted at intervals of 0.25 time units in
$\unicode[STIX]{x1D70E}=1$
. In each case, the solution is plotted at intervals of 0.25 time units in
![]() $\tilde{t}$
. Note this difference in output time interval from previous figures, and also that the scale of each plot is different.
$\tilde{t}$
. Note this difference in output time interval from previous figures, and also that the scale of each plot is different.

Figure 14. The pinch-off time,
![]() $\tilde{t}=\unicode[STIX]{x1D70F}_{c}$
as a function of
$\tilde{t}=\unicode[STIX]{x1D70F}_{c}$
as a function of
![]() $\unicode[STIX]{x1D6FC}$
when
$\unicode[STIX]{x1D6FC}$
when
![]() $\unicode[STIX]{x1D70E}=1$
. The change of curvature of this curve close to
$\unicode[STIX]{x1D70E}=1$
. The change of curvature of this curve close to
![]() $\unicode[STIX]{x1D6FC}=2.3$
is correlated with the change in distance along the plate at pinch-off shown in figure 15.
$\unicode[STIX]{x1D6FC}=2.3$
is correlated with the change in distance along the plate at pinch-off shown in figure 15.
Figure 15 shows the displacement of the contact line up the plate as a function of time,
![]() $\tilde{t}$
. After the initial motion, where the displacement is of
$\tilde{t}$
. After the initial motion, where the displacement is of
![]() $O(\tilde{t}^{4/3+\unicode[STIX]{x03C0}/3\unicode[STIX]{x1D6FC}})$
, its behaviour is almost linear, with a slight deceleration before pinch-off at time
$O(\tilde{t}^{4/3+\unicode[STIX]{x03C0}/3\unicode[STIX]{x1D6FC}})$
, its behaviour is almost linear, with a slight deceleration before pinch-off at time
![]() $\unicode[STIX]{x1D70F}_{c}$
. Note that when
$\unicode[STIX]{x1D70F}_{c}$
. Note that when
![]() $\unicode[STIX]{x1D6FC}=1.7$
, the contact line continues up the plate indefinitely (there is no pinch-off), and its displacement is of
$\unicode[STIX]{x1D6FC}=1.7$
, the contact line continues up the plate indefinitely (there is no pinch-off), and its displacement is of
![]() $O(\tilde{t}^{\unicode[STIX]{x1D6FE}})$
for
$O(\tilde{t}^{\unicode[STIX]{x1D6FE}})$
for
![]() $\tilde{t}\gg 1$
as the solution approaches its large-time asymptotic form, studied in Part 3. Figure 16 shows how the evolution of the free surface is affected by the dimensionless acceleration,
$\tilde{t}\gg 1$
as the solution approaches its large-time asymptotic form, studied in Part 3. Figure 16 shows how the evolution of the free surface is affected by the dimensionless acceleration,
![]() $\unicode[STIX]{x1D70E}$
, for the typical case,
$\unicode[STIX]{x1D70E}$
, for the typical case,
![]() $\unicode[STIX]{x1D6FC}=2.3$
. In each case, although the length and time scales are strongly dependent on
$\unicode[STIX]{x1D6FC}=2.3$
. In each case, although the length and time scales are strongly dependent on
![]() $\unicode[STIX]{x1D70E}$
, the shape of the free surface is not. We saw in Part 3 that the large-time solution of this problem is only affected by
$\unicode[STIX]{x1D70E}$
, the shape of the free surface is not. We saw in Part 3 that the large-time solution of this problem is only affected by
![]() $\unicode[STIX]{x1D70E}$
through a scaling of lengths and time. The situation is similar here, except that
$\unicode[STIX]{x1D70E}$
through a scaling of lengths and time. The situation is similar here, except that
![]() $\unicode[STIX]{x1D70E}$
does appear explicitly in the leading-order equations through the parameter
$\unicode[STIX]{x1D70E}$
does appear explicitly in the leading-order equations through the parameter
![]() $l^{-3}$
in (3.6), which multiplies the term that governs the effect of surface tension. These and other numerical simulations not presented here suggest that the effect of this term is mainly confined to regions of high curvature, and does not strongly affect the overall, qualitative nature of the evolution of the free surface.
$l^{-3}$
in (3.6), which multiplies the term that governs the effect of surface tension. These and other numerical simulations not presented here suggest that the effect of this term is mainly confined to regions of high curvature, and does not strongly affect the overall, qualitative nature of the evolution of the free surface.

Figure 15. The displacement of the contact line along the plate as a function of time, for
![]() $\unicode[STIX]{x1D6FC}=1.7,1.9,2.1,2.3,2.5,2.7$
and 2.9, with
$\unicode[STIX]{x1D6FC}=1.7,1.9,2.1,2.3,2.5,2.7$
and 2.9, with
![]() $\unicode[STIX]{x1D70E}=1$
. Note that the distance the contact line has travelled along the plate at pinch-off increases with
$\unicode[STIX]{x1D70E}=1$
. Note that the distance the contact line has travelled along the plate at pinch-off increases with
![]() $\unicode[STIX]{x1D6FC}$
until
$\unicode[STIX]{x1D6FC}$
until
![]() $\unicode[STIX]{x1D6FC}\approx 2.3$
, and that pinch-off occurs with the contact line successively closer to its original position as
$\unicode[STIX]{x1D6FC}\approx 2.3$
, and that pinch-off occurs with the contact line successively closer to its original position as
![]() $\unicode[STIX]{x1D6FC}$
increases further.
$\unicode[STIX]{x1D6FC}$
increases further.

Figure 16. The evolution of the free surface when
![]() $\unicode[STIX]{x1D6FC}=2.3$
for
$\unicode[STIX]{x1D6FC}=2.3$
for
![]() $\unicode[STIX]{x1D70E}=0.2$
, 1 and 5. The plots are at time intervals of 0.1 in
$\unicode[STIX]{x1D70E}=0.2$
, 1 and 5. The plots are at time intervals of 0.1 in
![]() $\tilde{t}$
. Note the different scales of the axes.
$\tilde{t}$
. Note the different scales of the axes.
4 Experimental results
In the experiments reported by Korsukova (Reference Korsukova2014), a programmable linear-drive mechanism mounted above an open rectangular channel was used to investigate the evolution of the free surface of a shallow liquid layer when displaced by an inclined (or vertical) plate, moving from rest with constant acceleration. The open channel (with horizontal base and vertical side walls) was of glass construction with internal dimensions
![]() $2355\times 298\times 200~\text{mm}^{3}$
. The drive mechanism was mounted above the rear half of the channel, giving a front working section of length 1260 mm. The channel and linear-drive mechanism were both held securely inside a rigid, other steel frame which was bolted to the floor of the laboratory.
$2355\times 298\times 200~\text{mm}^{3}$
. The drive mechanism was mounted above the rear half of the channel, giving a front working section of length 1260 mm. The channel and linear-drive mechanism were both held securely inside a rigid, other steel frame which was bolted to the floor of the laboratory.
The channel was partially filled with a liquid layer of uniform depth
![]() $h=25~\text{mm}$
. Three liquids were used: water (
$h=25~\text{mm}$
. Three liquids were used: water (
![]() $T=0.073~\text{N}~\text{m}^{-1}$
), glycerol (
$T=0.073~\text{N}~\text{m}^{-1}$
), glycerol (
![]() $T=0.064~\text{N}~\text{m}^{-1}$
) and a mixture of the two (
$T=0.064~\text{N}~\text{m}^{-1}$
) and a mixture of the two (
![]() $T=0.069~\text{N}~\text{m}^{-1}$
), corresponding to
$T=0.069~\text{N}~\text{m}^{-1}$
), corresponding to
![]() $Bo^{-1}\approx 10^{-2}$
. The rigid plate used to displace the liquid layer was of (polished) stainless steel construction and mounted below the linear-drive mechanism inside a housing designed so that the inclination angle of the plate could be varied between
$Bo^{-1}\approx 10^{-2}$
. The rigid plate used to displace the liquid layer was of (polished) stainless steel construction and mounted below the linear-drive mechanism inside a housing designed so that the inclination angle of the plate could be varied between
![]() $\unicode[STIX]{x1D6FC}=60^{\circ }$
and
$\unicode[STIX]{x1D6FC}=60^{\circ }$
and
![]() $140^{\circ }$
. The drive mechanism was programmed to move the plate (horizontally) with accelerations ranging from
$140^{\circ }$
. The drive mechanism was programmed to move the plate (horizontally) with accelerations ranging from
![]() $0.63g$
to
$0.63g$
to
![]() $4.3g$
. The static contact angle,
$4.3g$
. The static contact angle,
![]() $\unicode[STIX]{x1D6FD}_{0}$
, was varied by using a number of identical steel plates, one uncoated and the others with various hydrophilic and hydrophobic coatings applied to their surface. Note that the static contact angle is measured through the fluid, so that
$\unicode[STIX]{x1D6FD}_{0}$
, was varied by using a number of identical steel plates, one uncoated and the others with various hydrophilic and hydrophobic coatings applied to their surface. Note that the static contact angle is measured through the fluid, so that
![]() $\unicode[STIX]{x1D6FD}_{0}=\unicode[STIX]{x1D6FC}$
in the asymptotic solution, which corresponds to an initially horizontal free surface. A more detailed description of the experimental set-up can be found in Korsukova (Reference Korsukova2014).
$\unicode[STIX]{x1D6FD}_{0}=\unicode[STIX]{x1D6FC}$
in the asymptotic solution, which corresponds to an initially horizontal free surface. A more detailed description of the experimental set-up can be found in Korsukova (Reference Korsukova2014).
The deformation of the free surface, from the onset of the plate’s horizontal motion, was captured using high-speed photography. The free surface was visualised by adding fluorescent dye to the liquid and using a thin, vertical light sheet, directed upward through the base of the channel, to illuminate the liquid in front of the plate, in the plane perpendicular to the plate’s vertical centreline. As the plate accelerated, images of the illuminated region were recorded by a high-speed digital video camera (sampling at 3000 frames per second). Each captured image was post-processed to extract the free surface profile, which was then used to measure the dynamic contact angle, the contact line position and other key characteristics close to the contact line.

Figure 17. A comparison of the experimentally observed free surface with the inner solution, with
![]() $\unicode[STIX]{x1D6FC}=140^{\circ }$
,
$\unicode[STIX]{x1D6FC}=140^{\circ }$
,
![]() $\unicode[STIX]{x1D70E}=1.25$
(and hence
$\unicode[STIX]{x1D70E}=1.25$
(and hence
![]() $l\approx 1.85$
) and
$l\approx 1.85$
) and
![]() $T=0.07~\text{N}~\text{m}^{-1}$
.
$T=0.07~\text{N}~\text{m}^{-1}$
.

Figure 18. The experimentally observed contact angle (in degrees) as a function of time, for the same data set as that shown in figure 17.
Figures 17 and 18 show the experimentally observed free surface and contact angle. The measurement of the dynamic contact angle is very noisy, and the data shown suggest a contact angle of between
![]() $130$
and
$130$
and
![]() $140^{\circ }$
during the motion of the plate (the noise level is typically between
$140^{\circ }$
during the motion of the plate (the noise level is typically between
![]() $10$
and
$10$
and
![]() $15^{\circ }$
). This set of data should therefore be reasonably well described by our asymptotic theory, for which we assumed a constant contact angle, here
$15^{\circ }$
). This set of data should therefore be reasonably well described by our asymptotic theory, for which we assumed a constant contact angle, here
![]() $140^{\circ }$
. The qualitative agreement of the shape of the surface predicted by our asymptotic theory with that observed in this experiment is striking, and indicates that we have captured the key physical effects in our model. Moreover, recall that this flow is driven not by the local motion of the plate, but by the global effect of the paddle on the flow, which leads to a singularity at the contact line in the outer flow that emerges close to the contact line as the structure shown in figure 17. Note that the constant acceleration of the plate leads, in this case, to a structure that moves up the plate with close to constant velocity in both experiment and theory; a somewhat counterintuitive result that is not easy to predict by purely physical arguments. However, the theoretically predicted time scale for the flow is in error by a factor of three. The theoretical flow moves three times as fast as the experimentally observed flow.
$140^{\circ }$
. The qualitative agreement of the shape of the surface predicted by our asymptotic theory with that observed in this experiment is striking, and indicates that we have captured the key physical effects in our model. Moreover, recall that this flow is driven not by the local motion of the plate, but by the global effect of the paddle on the flow, which leads to a singularity at the contact line in the outer flow that emerges close to the contact line as the structure shown in figure 17. Note that the constant acceleration of the plate leads, in this case, to a structure that moves up the plate with close to constant velocity in both experiment and theory; a somewhat counterintuitive result that is not easy to predict by purely physical arguments. However, the theoretically predicted time scale for the flow is in error by a factor of three. The theoretical flow moves three times as fast as the experimentally observed flow.
There are several experimental factors that need to be taken into account in a discussion of this discrepancy.
-
(i) The initial, static contact angle,
 $150^{\circ }$
, is slightly larger than
$150^{\circ }$
, is slightly larger than
 $\unicode[STIX]{x1D6FC}=140^{\circ }$
, so the initial free surface is not precisely horizontal.
$\unicode[STIX]{x1D6FC}=140^{\circ }$
, so the initial free surface is not precisely horizontal. -
(ii) The acceleration of the paddle that drives the flow in the experiment is not perfectly constant. This means that, although we have taken this into account in estimating that
 $\unicode[STIX]{x1D70E}\approx 1.25$
in the experiment, this is definitely an estimate, and the time variation of the acceleration may be a significant factor. However, even allowing for a range of accelerations consistent with the observed motion of the plate does not account for the discrepancy between the time scales of theory and experiment.
$\unicode[STIX]{x1D70E}\approx 1.25$
in the experiment, this is definitely an estimate, and the time variation of the acceleration may be a significant factor. However, even allowing for a range of accelerations consistent with the observed motion of the plate does not account for the discrepancy between the time scales of theory and experiment. -
(iii) To avoid direct contact between stainless steel plate and glass channel, a narrow gap of 2 mm was left between the perimeter of the plate and inner surface of the channel walls. The flow induced by the accelerating plate was therefore not strictly two-dimensional, due to flow around and under the plate. To minimise this effect, measurements of the free surface were always taken in the plane normal to the vertical centreline of the plate, where edge effects were of least significance, especially at the small times considered here. The most significant edge effect was due to flow under the plate, but this was small, with the ratio of the liquid volume flowing under the plate to that displaced in front of the plate typically less than 8 %. This would certainly lead to a small error in the value of
 $A_{0}(\unicode[STIX]{x1D6FC})$
used in the theory for comparison.
$A_{0}(\unicode[STIX]{x1D6FC})$
used in the theory for comparison. -
(iv) We have assumed that the flow is irrotational, but the motion of the paddle may generate some vorticity in the outer flow, which could be significant.
-
(v) Although surface contamination may lead to a final surface tension coefficient lower than that measured initially, care was taken to prevent this. The surface tension of the fluid was measured both before and after the experiment and showed no significant difference.
-
(vi) The Bond number is not very small in the experiment (
 $Bo\approx 0.01$
,
$Bo\approx 0.01$
,
 $h_{c}/h\approx 0.1$
), so the asymptotic approximation we use is not highly accurate. More precisely, the correction term in the asymptotic expansion is of
$h_{c}/h\approx 0.1$
), so the asymptotic approximation we use is not highly accurate. More precisely, the correction term in the asymptotic expansion is of
 $O(Bo^{(\unicode[STIX]{x1D6FE}-2)/(3\unicode[STIX]{x1D6FE}-2)})=O(Bo^{(\unicode[STIX]{x03C0}-2\unicode[STIX]{x1D6FC})/(\unicode[STIX]{x03C0}+2\unicode[STIX]{x1D6FC})})\approx 0.37$
in this experiment.
$O(Bo^{(\unicode[STIX]{x1D6FE}-2)/(3\unicode[STIX]{x1D6FE}-2)})=O(Bo^{(\unicode[STIX]{x03C0}-2\unicode[STIX]{x1D6FC})/(\unicode[STIX]{x03C0}+2\unicode[STIX]{x1D6FC})})\approx 0.37$
in this experiment. -
(vii) The direct effect of the motion of the plate is neglected in the leading-order solutions shown in figure 17, but it appears at next order, which likely accounts for some of the difference between theory and experiment.
-
(viii) Viscosity has a strong effect on the dynamics of the contact angle (see our earlier discussion), but any other effect on the flow is confined to the boundary layer on the plate, and does not influence the flow on the length scales considered here.
In terms of our theory, the outer flow interacts with the inner flow through the parameters
![]() $l$
and
$l$
and
![]() $Bo$
. The parameter
$Bo$
. The parameter
![]() $l\equiv (A_{0}(\unicode[STIX]{x1D6FC})\unicode[STIX]{x1D70E}\sin \unicode[STIX]{x1D6FC})^{\unicode[STIX]{x1D6FE}/2}$
is determined by the constant applied acceleration,
$l\equiv (A_{0}(\unicode[STIX]{x1D6FC})\unicode[STIX]{x1D70E}\sin \unicode[STIX]{x1D6FC})^{\unicode[STIX]{x1D6FE}/2}$
is determined by the constant applied acceleration,
![]() $\unicode[STIX]{x1D70E}\equiv a/g$
, and the detailed nature of the outer solution, through
$\unicode[STIX]{x1D70E}\equiv a/g$
, and the detailed nature of the outer solution, through
![]() $A_{0}(\unicode[STIX]{x1D6FC})$
. It is therefore not unreasonable to use
$A_{0}(\unicode[STIX]{x1D6FC})$
. It is therefore not unreasonable to use
![]() $l$
as a fitting parameter, given the uncertainties described above. The Bond number,
$l$
as a fitting parameter, given the uncertainties described above. The Bond number,
![]() $Bo\equiv \unicode[STIX]{x1D70C}gh^{2}/T$
is also somewhat uncertain, through its dependence on
$Bo\equiv \unicode[STIX]{x1D70C}gh^{2}/T$
is also somewhat uncertain, through its dependence on
![]() $T$
. Figure 19 shows the effect of using
$T$
. Figure 19 shows the effect of using
![]() $l$
and
$l$
and
![]() $T$
as fitting parameters, which allows us to obtain good agreement with the experiment. However, the very low value of
$T$
as fitting parameters, which allows us to obtain good agreement with the experiment. However, the very low value of
![]() $T$
seems unlikely to be correct, so there remains some uncertainty as to the source of the discrepancy.
$T$
seems unlikely to be correct, so there remains some uncertainty as to the source of the discrepancy.

Figure 19. A comparison of the experimentally observed free surface with the inner solution, with
![]() $\unicode[STIX]{x1D6FC}=140^{\circ }$
,
$\unicode[STIX]{x1D6FC}=140^{\circ }$
,
![]() $l=0.4$
and
$l=0.4$
and
![]() $T=0.01~\text{N}~\text{m}^{-1}$
.
$T=0.01~\text{N}~\text{m}^{-1}$
.
5 Conclusion
In this paper, we have shown that when an inclined plate is driven with constant, horizontal acceleration into an initially stationary, horizontal layer of inviscid, incompressible fluid with depth much greater than the capillary length and constant contact angle, parasitic capillary waves form on the evolving free surface. For inclination angle
![]() $\unicode[STIX]{x1D6FC}<\unicode[STIX]{x1D6FC}_{c}$
, these waves decay away on a time scale
$\unicode[STIX]{x1D6FC}<\unicode[STIX]{x1D6FC}_{c}$
, these waves decay away on a time scale
![]() $Bo^{-1/(3\unicode[STIX]{x1D6FE}-1)}\sqrt{h/g}$
, and surface tension has a negligible effect on the later evolution of the surface. However, when
$Bo^{-1/(3\unicode[STIX]{x1D6FE}-1)}\sqrt{h/g}$
, and surface tension has a negligible effect on the later evolution of the surface. However, when
![]() $\unicode[STIX]{x1D6FC}>\unicode[STIX]{x1D6FC}_{c}$
, the amplitude of these parasitic capillary waves grows and regions of high curvature develop. These eventually lead to pinch-off of the free surface at some finite time that also scales with
$\unicode[STIX]{x1D6FC}>\unicode[STIX]{x1D6FC}_{c}$
, the amplitude of these parasitic capillary waves grows and regions of high curvature develop. These eventually lead to pinch-off of the free surface at some finite time that also scales with
![]() $Bo^{-1/(3\unicode[STIX]{x1D6FE}-1)}\sqrt{h/g}$
. We were able to compare a numerical solution of the initial boundary value problem with an experimental realisation of this flow. Although there was a significant discrepancy in the time scale of the flow, which could be due to a number of factors discussed in the paper, the qualitative form of the developing parasitic capillary wave was in excellent agreement with our numerical solution.
$Bo^{-1/(3\unicode[STIX]{x1D6FE}-1)}\sqrt{h/g}$
. We were able to compare a numerical solution of the initial boundary value problem with an experimental realisation of this flow. Although there was a significant discrepancy in the time scale of the flow, which could be due to a number of factors discussed in the paper, the qualitative form of the developing parasitic capillary wave was in excellent agreement with our numerical solution.
The case of an initially horizontal layer of fluid (contact angle equal to plate inclination) is a rather special one. Although the experimental result presented here suggests that a small deviation of the contact angle from horizontal may not have a strong effect on the evolution of the free surface, large deviations do have a strong effect (Korsukova Reference Korsukova2014). In a later paper we will report on the effect of a constant, non-horizontal contact angle, and show that in this case the contact angle has a stronger effect on the evolution of the flow than the inclination of the plate (these are equal in the results reported here).
Acknowledgement
This work was supported by the Engineering and Physical Sciences Research Council (grant no. EP/H007830/1).