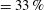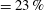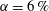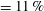1 Introduction
In the maritime industry, air lubrication is seen as one of the most promising techniques to reduce the overall fuel consumption (Kodama et al. Reference Kodama, Kakugawa, Takahashi and Kawashima2000; Foeth Reference Foeth2008; Mäkiharju, Perlin & Ceccio Reference Mäkiharju, Perlin and Ceccio2012). Air lubrication has been studied for several decades, and it is found that a few per cent of air can significantly decrease the overall friction, e.g. with 4 % bubbles, drag reductions up to 40 % were shown (van Gils et al. Reference van Gils, Narezo Guzman, Sun and Lohse2013; Verschoof et al. Reference Verschoof, van der Veen, Sun and Lohse2016). Notwithstanding its clear industrial potential, it remains difficult to translate highly controlled laboratory results to drag reduction in large-scale vessels. So far, the vast majority of studies on bubble drag reduction (DR) have been performed in test facilities with purified water and smooth walls: see e.g. the review articles by Ceccio (Reference Ceccio2010) and Murai (Reference Murai2014). However, many surfaces in industry are rough to some extent, and also initially smooth surfaces can become rough by means of corrosion, cavitation, mineral scaling and (bio)fouling (Schultz Reference Schultz2007; Schultz et al. Reference Schultz, Bendick, Holm and Hertel2011). Furthermore, the dynamics of bubbles is strongly affected by any dissolved ions in oceanic water and surfactants (Takagi, Ogasawara & Matsumoto Reference Takagi, Ogasawara and Matsumoto2008; Takagi & Matsumoto Reference Takagi and Matsumoto2011). As the conditions in controlled experiments and real applications are so different, one can expect that bubble DR experiments will lead to very different results in practice. Only a limited number of studies focused on ‘non-ideal’ DR, either through wall roughness (Deutsch et al. Reference Deutsch, Moeny, Fontaine and Petrie2004; Van den Berg et al. Reference Van den Berg, van Gils, Lathrop and Lohse2007; Elbing et al. Reference Elbing, Winkel, Lay, Ceccio, Dowling and Perlin2008, Reference Elbing, Mäkiharju, Wiggins, Perlin, Dowling and Ceccio2013), surfactants or seawater (Takahashi et al. Reference Takahashi, Kakugawa, Nagaya, Yanagihara and Kodama2001; Winkel et al. Reference Winkel, Ceccio, Dowling and Perlin2004; Shen, Perlin & Ceccio Reference Shen, Perlin and Ceccio2006; Elbing et al. Reference Elbing, Winkel, Lay, Ceccio, Dowling and Perlin2008; Verschoof et al. Reference Verschoof, van der Veen, Sun and Lohse2016), and their results are somewhat inconsistent. Some studies found that wall roughness completely eliminates any drag reduction (Van den Berg et al. Reference Van den Berg, van Gils, Lathrop and Lohse2007). Another study with rough-wall flat plate measurements showed that bubble DR or air layer DR can still be effective, at the cost, however, of an increased required air injection flux as the roughness forces the air away from the wall (Elbing et al. Reference Elbing, Mäkiharju, Wiggins, Perlin, Dowling and Ceccio2013). A third study showed that roughness can even enhance drag reduction (Deutsch et al. Reference Deutsch, Moeny, Fontaine and Petrie2004). Given this variety of conclusions, there is a clear need to better understand the influence of wall roughness on bubble drag reduction.
In this work, we study the effect of wall roughness on bubble drag reduction. To do so, we employ the Taylor–Couette (TC) system, i.e. the flow between two concentric, independently rotating cylinders (Fardin, Perge & Taberlet Reference Fardin, Perge and Taberlet2014; Grossmann, Lohse & Sun Reference Grossmann, Lohse and Sun2016). TC flow is one of the canonical flow systems in which fluid mechanics concepts and theories are tested. Among the advantages of using a TC set-up are the ease with which the global void fraction
![]() $\unicode[STIX]{x1D6FC}$
is controlled, the absence of any streamwise spatial transients and, as it is a closed system, an exact balance that connects the global torque measurements with the local energy dissipation rate. The driving and response of the system are characterized by the Taylor number
$\unicode[STIX]{x1D6FC}$
is controlled, the absence of any streamwise spatial transients and, as it is a closed system, an exact balance that connects the global torque measurements with the local energy dissipation rate. The driving and response of the system are characterized by the Taylor number
![]() $Ta$
and the Nusselt number
$Ta$
and the Nusselt number
![]() $Nu_{\unicode[STIX]{x1D714}}$
, respectively (Grossmann et al.
Reference Grossmann, Lohse and Sun2016). The Nusselt number is defined as the ratio of the convective momentum transport to the diffusive flux, and using it underlines the close analogy between Taylor–Couette flow and Rayleigh–Bénard convection (Eckhardt, Grossmann & Lohse Reference Eckhardt, Grossmann and Lohse2007). In the currently studied parameter regime, an effective scaling of
$Nu_{\unicode[STIX]{x1D714}}$
, respectively (Grossmann et al.
Reference Grossmann, Lohse and Sun2016). The Nusselt number is defined as the ratio of the convective momentum transport to the diffusive flux, and using it underlines the close analogy between Taylor–Couette flow and Rayleigh–Bénard convection (Eckhardt, Grossmann & Lohse Reference Eckhardt, Grossmann and Lohse2007). In the currently studied parameter regime, an effective scaling of
![]() $Nu_{\unicode[STIX]{x1D714}}\propto Ta^{0.4}$
is observed (van Gils et al.
Reference van Gils, Huisman, Bruggert, Sun and Lohse2011b
). The TC set-up has been used frequently to study (bubble) drag reduction in turbulent flows (van den Berg et al.
Reference van den Berg, Luther, Lathrop and Lohse2005; van Gils et al.
Reference van Gils, Narezo Guzman, Sun and Lohse2013; Rosenberg et al.
Reference Rosenberg, van Buren, Matthew and Smits2016; Saranadhi et al.
Reference Saranadhi, Chen, Kleingartner, Srinivasan, Cohen and McKinley2016; Verschoof et al.
Reference Verschoof, van der Veen, Sun and Lohse2016), even numerically (Sugiyama, Calzavarini & Lohse Reference Sugiyama, Calzavarini and Lohse2008; Spandan, Verzicco & Lohse Reference Spandan, Verzicco and Lohse2017). In these studies, it was shown that a small air fraction can considerably reduce the drag. For example, with a void fraction of
$Nu_{\unicode[STIX]{x1D714}}\propto Ta^{0.4}$
is observed (van Gils et al.
Reference van Gils, Huisman, Bruggert, Sun and Lohse2011b
). The TC set-up has been used frequently to study (bubble) drag reduction in turbulent flows (van den Berg et al.
Reference van den Berg, Luther, Lathrop and Lohse2005; van Gils et al.
Reference van Gils, Narezo Guzman, Sun and Lohse2013; Rosenberg et al.
Reference Rosenberg, van Buren, Matthew and Smits2016; Saranadhi et al.
Reference Saranadhi, Chen, Kleingartner, Srinivasan, Cohen and McKinley2016; Verschoof et al.
Reference Verschoof, van der Veen, Sun and Lohse2016), even numerically (Sugiyama, Calzavarini & Lohse Reference Sugiyama, Calzavarini and Lohse2008; Spandan, Verzicco & Lohse Reference Spandan, Verzicco and Lohse2017). In these studies, it was shown that a small air fraction can considerably reduce the drag. For example, with a void fraction of
![]() $\unicode[STIX]{x1D6FC}=4\,\%$
, a drag reduction of
$\unicode[STIX]{x1D6FC}=4\,\%$
, a drag reduction of
![]() $40\,\%$
was observed (van Gils et al.
Reference van Gils, Narezo Guzman, Sun and Lohse2013; Verschoof et al.
Reference Verschoof, van der Veen, Sun and Lohse2016), which is significantly larger than the trivial effects of affected effective density and viscosity. These studies highlighted the importance of bubble deformability for large drag reduction, and thus a sufficiently large Weber number
$40\,\%$
was observed (van Gils et al.
Reference van Gils, Narezo Guzman, Sun and Lohse2013; Verschoof et al.
Reference Verschoof, van der Veen, Sun and Lohse2016), which is significantly larger than the trivial effects of affected effective density and viscosity. These studies highlighted the importance of bubble deformability for large drag reduction, and thus a sufficiently large Weber number
![]() $We=\unicode[STIX]{x1D70C}D_{b}u^{2}/\unicode[STIX]{x1D70E}$
, in which
$We=\unicode[STIX]{x1D70C}D_{b}u^{2}/\unicode[STIX]{x1D70E}$
, in which
![]() $\unicode[STIX]{x1D70C}$
is the fluid density,
$\unicode[STIX]{x1D70C}$
is the fluid density,
![]() $D_{b}$
the bubble diameter,
$D_{b}$
the bubble diameter,
![]() $u$
a characteristic velocity and
$u$
a characteristic velocity and
![]() $\unicode[STIX]{x1D70E}$
the interfacial surface tension. It was shown that large Weber number bubbles, i.e. large and deformable bubbles, are crucial to efficiently reduce the drag. The bubbles experience multiple forces. Most important are (i) centripetal forces, pushing air towards the inner cylinder, (ii) buoyancy forces, pushing air towards the top and (iii) turbulent fluctuations, mixing the bubbles throughout the flow. Large bubbles are hardly affected by the turbulent fluctuations, and are therefore strongly pushed towards the inner cylinder. The role of the buoyancy forces decreases with increasing rotation rates. Wall roughness, on the other hand, obviously increases the friction. Its effects have been studied extensively for single-phase turbulence flows, mostly in pipe or channel flow configurations given their industrial relevance: see e.g. Marusic et al. (Reference Marusic, McKeon, Monkewitz, Nagib, Smits and Sreenivasan2010), Flack & Schultz (Reference Flack and Schultz2014) and references therein. For TC flow, adding sufficiently large, rough ribs results in a
$\unicode[STIX]{x1D70E}$
the interfacial surface tension. It was shown that large Weber number bubbles, i.e. large and deformable bubbles, are crucial to efficiently reduce the drag. The bubbles experience multiple forces. Most important are (i) centripetal forces, pushing air towards the inner cylinder, (ii) buoyancy forces, pushing air towards the top and (iii) turbulent fluctuations, mixing the bubbles throughout the flow. Large bubbles are hardly affected by the turbulent fluctuations, and are therefore strongly pushed towards the inner cylinder. The role of the buoyancy forces decreases with increasing rotation rates. Wall roughness, on the other hand, obviously increases the friction. Its effects have been studied extensively for single-phase turbulence flows, mostly in pipe or channel flow configurations given their industrial relevance: see e.g. Marusic et al. (Reference Marusic, McKeon, Monkewitz, Nagib, Smits and Sreenivasan2010), Flack & Schultz (Reference Flack and Schultz2014) and references therein. For TC flow, adding sufficiently large, rough ribs results in a
![]() $Nu_{\unicode[STIX]{x1D714}}\propto Ta^{1/2}$
scaling, rather than the aforementioned
$Nu_{\unicode[STIX]{x1D714}}\propto Ta^{1/2}$
scaling, rather than the aforementioned
![]() $Nu_{\unicode[STIX]{x1D714}}\propto Ta^{0.4}$
smooth-wall scaling (Cadot et al.
Reference Cadot, Couder, Daerr, Douady and Tsinober1997; van den Berg et al.
Reference van den Berg, Doering, Lohse and Lathrop2003; Zhu et al.
Reference Zhu, Verschoof, Bakhuis, Huisman, Verzicco, Sun and Lohse2018). In this regime, the main contribution to the torque originates from the pressure force acting on the ribs rather than the skin friction on the cylinder (Zhu et al.
Reference Zhu, Verschoof, Bakhuis, Huisman, Verzicco, Sun and Lohse2018). The
$Nu_{\unicode[STIX]{x1D714}}\propto Ta^{0.4}$
smooth-wall scaling (Cadot et al.
Reference Cadot, Couder, Daerr, Douady and Tsinober1997; van den Berg et al.
Reference van den Berg, Doering, Lohse and Lathrop2003; Zhu et al.
Reference Zhu, Verschoof, Bakhuis, Huisman, Verzicco, Sun and Lohse2018). In this regime, the main contribution to the torque originates from the pressure force acting on the ribs rather than the skin friction on the cylinder (Zhu et al.
Reference Zhu, Verschoof, Bakhuis, Huisman, Verzicco, Sun and Lohse2018). The
![]() $Nu_{\unicode[STIX]{x1D714}}\propto Ta^{1/2}$
scaling, mathematically equivalent to a constant friction coefficient in the fully rough regime, is the mathematical upper bound to the transport of momentum. In this regime, the roughness decreases the near-wall velocity gradient, whereas the streamwise velocity fluctuations are increased. The bubble dynamics is largely governed by the motion of the surrounding fluid, but to which extent any drag reduction is affected by the changed fluid motion is unknown.
$Nu_{\unicode[STIX]{x1D714}}\propto Ta^{1/2}$
scaling, mathematically equivalent to a constant friction coefficient in the fully rough regime, is the mathematical upper bound to the transport of momentum. In this regime, the roughness decreases the near-wall velocity gradient, whereas the streamwise velocity fluctuations are increased. The bubble dynamics is largely governed by the motion of the surrounding fluid, but to which extent any drag reduction is affected by the changed fluid motion is unknown.
A number of studies focused on wall modifications to stimulate air to attach to the inner cylinder wall of Taylor–Couette flow, either by a hydrophobic coating (Srinivasan et al. Reference Srinivasan, Kleingartner, Gilbert, Cohen, Milne and McKinley2015) or by using cavitors to try to create an air layer (Verschoof et al. Reference Verschoof, Bakhuis, Bullee, Huisman, Sun and Lohse2018). Van den Berg et al. (Reference Van den Berg, van Gils, Lathrop and Lohse2007) studied the effects of roughness on bubble drag reduction, and found that ribs attached to both cylinders prevent bubbles from reducing the overall friction. Therefore, it was suggested that bubbly drag reduction is a boundary layer effect. However, the exact reason why the drag reduction was lost remained elusive. Therefore, here we aim to repeat and extend those experiments in a more accurate and controlled set-up and to visualize the flow, to better understand the physics of the aforementioned conclusions.

Figure 1. Experimental set-up. (a) Top view schematic of the T
![]() $^{3}$
C facility. We attached six vertical transverse ribs (not to scale) equally distributed around the perimeter of the inner cylinder, the outer cylinder or both cylinders. We also measure a smooth-wall case without any ribs. (b) Vertical cross-section of the set-up at rest, showing the position of the torque sensor. To control the void fraction, we fill the cylinder only partially with water, so that the void fraction
$^{3}$
C facility. We attached six vertical transverse ribs (not to scale) equally distributed around the perimeter of the inner cylinder, the outer cylinder or both cylinders. We also measure a smooth-wall case without any ribs. (b) Vertical cross-section of the set-up at rest, showing the position of the torque sensor. To control the void fraction, we fill the cylinder only partially with water, so that the void fraction
![]() $\unicode[STIX]{x1D6FC}$
is controlled by measuring the relative height of the water level. (c) Vertical cross-section of the set-up during a measurement. The free surface disappears, and all air is entrained by the turbulent flow (bubbles not to scale).
$\unicode[STIX]{x1D6FC}$
is controlled by measuring the relative height of the water level. (c) Vertical cross-section of the set-up during a measurement. The free surface disappears, and all air is entrained by the turbulent flow (bubbles not to scale).
2 Experimental method
The experiments are performed in the Twente Turbulent Taylor–Couette facility (T
![]() $^{3}$
C) (van Gils et al.
Reference van Gils, Bruggert, Lathrop, Sun and Lohse2011a
), in which the flow is fully turbulent. TC flow is driven by the angular velocity of the inner and outer cylinder, denoted by
$^{3}$
C) (van Gils et al.
Reference van Gils, Bruggert, Lathrop, Sun and Lohse2011a
), in which the flow is fully turbulent. TC flow is driven by the angular velocity of the inner and outer cylinder, denoted by
![]() $\unicode[STIX]{x1D714}_{i}$
and
$\unicode[STIX]{x1D714}_{i}$
and
![]() $\unicode[STIX]{x1D714}_{o}$
, respectively. The set-up has a height of
$\unicode[STIX]{x1D714}_{o}$
, respectively. The set-up has a height of
![]() $L=927~\text{mm}$
, an inner radius
$L=927~\text{mm}$
, an inner radius
![]() $r_{i}=200~\text{mm}$
and an outer radius
$r_{i}=200~\text{mm}$
and an outer radius
![]() $r_{o}=279.4~\text{mm}$
, giving a gap width
$r_{o}=279.4~\text{mm}$
, giving a gap width
![]() $d=r_{o}-r_{i}=79.4~\text{mm}$
. The geometry can therefore be described by two geometric parameters: the radius ratio
$d=r_{o}-r_{i}=79.4~\text{mm}$
. The geometry can therefore be described by two geometric parameters: the radius ratio
![]() $\unicode[STIX]{x1D702}=r_{i}/r_{o}=0.716$
and the aspect ratio
$\unicode[STIX]{x1D702}=r_{i}/r_{o}=0.716$
and the aspect ratio
![]() $\unicode[STIX]{x1D6E4}=L/d=11.7$
; see also figure 1(a). The inner cylinder and outer cylinder rotate up to
$\unicode[STIX]{x1D6E4}=L/d=11.7$
; see also figure 1(a). The inner cylinder and outer cylinder rotate up to
![]() $f_{i}=\unicode[STIX]{x1D714}_{i}/(2\unicode[STIX]{x03C0})=10$
Hz and
$f_{i}=\unicode[STIX]{x1D714}_{i}/(2\unicode[STIX]{x03C0})=10$
Hz and
![]() $f_{o}=-4$
Hz, respectively. These result in two Reynolds numbers,
$f_{o}=-4$
Hz, respectively. These result in two Reynolds numbers,
![]() $Re_{i,o}=\unicode[STIX]{x1D714}_{i,o}r_{i,o}(r_{o}-r_{i})/\unicode[STIX]{x1D708}$
, respectively, in which
$Re_{i,o}=\unicode[STIX]{x1D714}_{i,o}r_{i,o}(r_{o}-r_{i})/\unicode[STIX]{x1D708}$
, respectively, in which
![]() $\unicode[STIX]{x1D708}$
is the viscosity of the working fluid. The rotation ratio
$\unicode[STIX]{x1D708}$
is the viscosity of the working fluid. The rotation ratio
![]() $a$
is defined as
$a$
is defined as
![]() $a=-\unicode[STIX]{x1D714}_{o}/\unicode[STIX]{x1D714}_{i}$
. We here express the driving using the Taylor number
$a=-\unicode[STIX]{x1D714}_{o}/\unicode[STIX]{x1D714}_{i}$
. We here express the driving using the Taylor number
![]() $Ta=[(1+\unicode[STIX]{x1D702})^{4}/(64\unicode[STIX]{x1D702}^{2})]d^{2}(r_{i}+r_{o})^{2}(\unicode[STIX]{x1D714}_{i}-\unicode[STIX]{x1D714}_{o})^{2}\unicode[STIX]{x1D708}^{-2}\propto (Re_{i}-\unicode[STIX]{x1D702}Re_{o})^{2}$
, which thus incorporates the rotation of both cylinders in one dimensionless number. In the current study, we measure at Taylor numbers of
$Ta=[(1+\unicode[STIX]{x1D702})^{4}/(64\unicode[STIX]{x1D702}^{2})]d^{2}(r_{i}+r_{o})^{2}(\unicode[STIX]{x1D714}_{i}-\unicode[STIX]{x1D714}_{o})^{2}\unicode[STIX]{x1D708}^{-2}\propto (Re_{i}-\unicode[STIX]{x1D702}Re_{o})^{2}$
, which thus incorporates the rotation of both cylinders in one dimensionless number. In the current study, we measure at Taylor numbers of
![]() $O(10^{12})$
, or, equivalently, Reynolds numbers up to
$O(10^{12})$
, or, equivalently, Reynolds numbers up to
![]() $O(10^{6})$
. The primary response parameter is the torque
$O(10^{6})$
. The primary response parameter is the torque
![]() $\unicode[STIX]{x1D70F}$
necessary to maintain the inner cylinder at a constant angular velocity. The torque is measured with a co-axial torque transducer (Honeywell Hollow Reaction Torque Sensor 2404-1K, maximum capacity of 115 Nm), which is located inside the inner cylinder to avoid measurement errors due to seal and bearing friction: see figure 1(b). The torque is made dimensionless with the torque for laminar non-vertical flow, resulting in the Nusselt number
$\unicode[STIX]{x1D70F}$
necessary to maintain the inner cylinder at a constant angular velocity. The torque is measured with a co-axial torque transducer (Honeywell Hollow Reaction Torque Sensor 2404-1K, maximum capacity of 115 Nm), which is located inside the inner cylinder to avoid measurement errors due to seal and bearing friction: see figure 1(b). The torque is made dimensionless with the torque for laminar non-vertical flow, resulting in the Nusselt number
![]() $Nu_{\unicode[STIX]{x1D714}}=\unicode[STIX]{x1D70F}/\unicode[STIX]{x1D70F}_{lam}$
, with
$Nu_{\unicode[STIX]{x1D714}}=\unicode[STIX]{x1D70F}/\unicode[STIX]{x1D70F}_{lam}$
, with
![]() $\unicode[STIX]{x1D70F}_{lam}=4\unicode[STIX]{x03C0}L\unicode[STIX]{x1D70C}\unicode[STIX]{x1D708}r_{i}^{2}r_{o}^{2}(\unicode[STIX]{x1D714}_{i}-\unicode[STIX]{x1D714}_{o})/(r_{o}^{2}-r_{i}^{2})$
. The flow is cooled through both endplates to counteract viscous heating, keeping the water temperature constant within
$\unicode[STIX]{x1D70F}_{lam}=4\unicode[STIX]{x03C0}L\unicode[STIX]{x1D70C}\unicode[STIX]{x1D708}r_{i}^{2}r_{o}^{2}(\unicode[STIX]{x1D714}_{i}-\unicode[STIX]{x1D714}_{o})/(r_{o}^{2}-r_{i}^{2})$
. The flow is cooled through both endplates to counteract viscous heating, keeping the water temperature constant within
![]() $T=21\pm 0.5~^{\circ }\text{C}$
. Although the effective viscosity and density are altered by the presence of bubbles, we chose to consequently use the pure water material properties, as we are interested in the net changes in drag.
$T=21\pm 0.5~^{\circ }\text{C}$
. Although the effective viscosity and density are altered by the presence of bubbles, we chose to consequently use the pure water material properties, as we are interested in the net changes in drag.
The cylinders are made rough by attaching six transverse ribs over the entire height of the cylinders, as shown in figure 1(a). The rib dimensions are 6 mm by 6 mm, corresponding to 7.5 % of the gap width, and to
![]() $O(10^{3})$
in wall units, depending on the Taylor number and roughness case. We study the torque and resulting drag reduction for four cases: both cylinders smooth (SS), both cylinders rough (RR), and roughness either only on the inner cylinder (RS) or only on the outer cylinder (SR). We here chose to apply rib roughness, which, for the RR case, causes the flow to be in the ‘fully rough’ state, or the ‘asymptotic ultimate turbulence’ regime (Zhu et al.
Reference Zhu, Verschoof, Bakhuis, Huisman, Verzicco, Sun and Lohse2018) in the studied parameter regime. In this regime, the behaviour in the boundary layers becomes independent of the viscosity. Consequently, a
$O(10^{3})$
in wall units, depending on the Taylor number and roughness case. We study the torque and resulting drag reduction for four cases: both cylinders smooth (SS), both cylinders rough (RR), and roughness either only on the inner cylinder (RS) or only on the outer cylinder (SR). We here chose to apply rib roughness, which, for the RR case, causes the flow to be in the ‘fully rough’ state, or the ‘asymptotic ultimate turbulence’ regime (Zhu et al.
Reference Zhu, Verschoof, Bakhuis, Huisman, Verzicco, Sun and Lohse2018) in the studied parameter regime. In this regime, the behaviour in the boundary layers becomes independent of the viscosity. Consequently, a
![]() $Nu_{\unicode[STIX]{x1D714}}\propto Ta^{1/2}$
is observed rather than the effective
$Nu_{\unicode[STIX]{x1D714}}\propto Ta^{1/2}$
is observed rather than the effective
![]() $Nu_{\unicode[STIX]{x1D714}}\propto Ta^{0.4}$
scaling found for the smooth-wall case in the currently studied parameter regime (Kraichnan Reference Kraichnan1962; van Gils et al.
Reference van Gils, Huisman, Bruggert, Sun and Lohse2011b
; Zhu et al.
Reference Zhu, Verschoof, Bakhuis, Huisman, Verzicco, Sun and Lohse2018). For the cases of ribs on a single cylinder, the exponent
$Nu_{\unicode[STIX]{x1D714}}\propto Ta^{0.4}$
scaling found for the smooth-wall case in the currently studied parameter regime (Kraichnan Reference Kraichnan1962; van Gils et al.
Reference van Gils, Huisman, Bruggert, Sun and Lohse2011b
; Zhu et al.
Reference Zhu, Verschoof, Bakhuis, Huisman, Verzicco, Sun and Lohse2018). For the cases of ribs on a single cylinder, the exponent
![]() $\unicode[STIX]{x1D6FE}$
of the
$\unicode[STIX]{x1D6FE}$
of the
![]() $Nu_{\unicode[STIX]{x1D714}}\propto Ta^{\unicode[STIX]{x1D6FE}}$
-scaling is between these two bounds.
$Nu_{\unicode[STIX]{x1D714}}\propto Ta^{\unicode[STIX]{x1D6FE}}$
-scaling is between these two bounds.
The gap is either partially or completely filled with water, so that the void fraction is precisely set at
![]() $0\,\%\leqslant \unicode[STIX]{x1D6FC}\leqslant 6\,\%$
: see figure 1(b). We determine the void fraction with both cylinders at rest. During a flow measurement, the air is distributed over the height of the cylinder because of turbulent mixing: see figure 1(c). The uncertainty in the void fraction
$0\,\%\leqslant \unicode[STIX]{x1D6FC}\leqslant 6\,\%$
: see figure 1(b). We determine the void fraction with both cylinders at rest. During a flow measurement, the air is distributed over the height of the cylinder because of turbulent mixing: see figure 1(c). The uncertainty in the void fraction
![]() $\unicode[STIX]{x1D6FC}$
is around
$\unicode[STIX]{x1D6FC}$
is around
![]() $\pm 0.2\,\%$
. We note that a perfect homogeneous axial distribution is not feasable, even with continuous bubble injection through the bottom end cap (as was shown in van Gils et al. (Reference van Gils, Narezo Guzman, Sun and Lohse2013)), but it becomes more homogeneous with increasing Taylor number.
$\pm 0.2\,\%$
. We note that a perfect homogeneous axial distribution is not feasable, even with continuous bubble injection through the bottom end cap (as was shown in van Gils et al. (Reference van Gils, Narezo Guzman, Sun and Lohse2013)), but it becomes more homogeneous with increasing Taylor number.

Figure 2. (a) Dimensionless angular velocity flux
![]() $Nu_{\unicode[STIX]{x1D714}}$
as a function of
$Nu_{\unicode[STIX]{x1D714}}$
as a function of
![]() $Ta$
for
$Ta$
for
![]() $\unicode[STIX]{x1D6FC}=0\,\%$
and
$\unicode[STIX]{x1D6FC}=0\,\%$
and
![]() $\unicode[STIX]{x1D6FC}=6\,\%$
. To increase readability, we do not show
$\unicode[STIX]{x1D6FC}=6\,\%$
. To increase readability, we do not show
![]() $Nu_{\unicode[STIX]{x1D714}}$
for
$Nu_{\unicode[STIX]{x1D714}}$
for
![]() $\unicode[STIX]{x1D6FC}=\{2\,\%,4\,\%\}$
, which are used to calculate the DR shown in figure 3. The two short black lines indicate the
$\unicode[STIX]{x1D6FC}=\{2\,\%,4\,\%\}$
, which are used to calculate the DR shown in figure 3. The two short black lines indicate the
![]() $Nu_{\unicode[STIX]{x1D714}}\propto Ta^{\unicode[STIX]{x1D6FE}}$
scaling relations for the pure liquid cases. The exponents are
$Nu_{\unicode[STIX]{x1D714}}\propto Ta^{\unicode[STIX]{x1D6FE}}$
scaling relations for the pure liquid cases. The exponents are
![]() $\unicode[STIX]{x1D6FE}=0.4$
and
$\unicode[STIX]{x1D6FE}=0.4$
and
![]() $\unicode[STIX]{x1D6FE}=1/2$
for the SS and RR cases, respectively. (b) Resulting drag reduction as a function of
$\unicode[STIX]{x1D6FE}=1/2$
for the SS and RR cases, respectively. (b) Resulting drag reduction as a function of
![]() $Ta$
. The outer cylinder is stationary. The DR is calculated with (3.1). Typical error bars are shown.
$Ta$
. The outer cylinder is stationary. The DR is calculated with (3.1). Typical error bars are shown.

Figure 3. Drag reduction percentages as a function of
![]() $Ta$
for all roughness cases. In the RR case, the highest achievable Taylor number is slightly smaller due to experimental limitations. The outer cylinder is stationary. The DR is calculated with (3.1). Typical error bars are shown.
$Ta$
for all roughness cases. In the RR case, the highest achievable Taylor number is slightly smaller due to experimental limitations. The outer cylinder is stationary. The DR is calculated with (3.1). Typical error bars are shown.
3 Results
We measure the torque and present our findings in figures 2 and 3. The drag reduction is calculated as
in which we compare the
![]() $Nu_{\unicode[STIX]{x1D714}}$
values for the same roughness case. In figure 2, we show the Nusselt number and resulting drag reduction for all roughness cases. As was shown before,
$Nu_{\unicode[STIX]{x1D714}}$
values for the same roughness case. In figure 2, we show the Nusselt number and resulting drag reduction for all roughness cases. As was shown before,
![]() $Nu_{\unicode[STIX]{x1D714}}$
depends tremendously on the applied roughness (Zhu et al.
Reference Zhu, Verschoof, Bakhuis, Huisman, Verzicco, Sun and Lohse2018). In the current study, however, we are more interested in the relative bubbly drag reduction as compared to the smooth-wall case, rather than the absolute friction increase by roughness. From figure 2 two different regimes can be distinguished: we observe strong drag reduction for the SS and RS cases, up to DR
$Nu_{\unicode[STIX]{x1D714}}$
depends tremendously on the applied roughness (Zhu et al.
Reference Zhu, Verschoof, Bakhuis, Huisman, Verzicco, Sun and Lohse2018). In the current study, however, we are more interested in the relative bubbly drag reduction as compared to the smooth-wall case, rather than the absolute friction increase by roughness. From figure 2 two different regimes can be distinguished: we observe strong drag reduction for the SS and RS cases, up to DR
![]() $=33\,\%$
with a void fraction of
$=33\,\%$
with a void fraction of
![]() $\unicode[STIX]{x1D6FC}=6\,\%$
, whereas for the SR and RR cases, the DR is only weak, with the same void fraction never exceeding DR
$\unicode[STIX]{x1D6FC}=6\,\%$
, whereas for the SR and RR cases, the DR is only weak, with the same void fraction never exceeding DR
![]() $=12\,\%$
.
$=12\,\%$
.
To study the DR per roughness case further, we show the drag reduction for void fractions of
![]() $2\,\%$
,
$2\,\%$
,
![]() $4\,\%$
and
$4\,\%$
and
![]() $6\,\%$
in figure 3. The DR increased monotonically with increasing void fraction for all cases. In the weak drag reduction cases (SR and RR), the DR is quite close to the trivial effect of reduced global density, which equals
$6\,\%$
in figure 3. The DR increased monotonically with increasing void fraction for all cases. In the weak drag reduction cases (SR and RR), the DR is quite close to the trivial effect of reduced global density, which equals
![]() $\unicode[STIX]{x1D70C}_{eff}=\unicode[STIX]{x1D70C}(1-\unicode[STIX]{x1D6FC})+\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70C}_{air}\approx \unicode[STIX]{x1D70C}(1-\unicode[STIX]{x1D6FC})$
, in which
$\unicode[STIX]{x1D70C}_{eff}=\unicode[STIX]{x1D70C}(1-\unicode[STIX]{x1D6FC})+\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70C}_{air}\approx \unicode[STIX]{x1D70C}(1-\unicode[STIX]{x1D6FC})$
, in which
![]() $\unicode[STIX]{x1D70C}_{air}$
is the air density. For the RS and SS cases, however, the drag reduction is significantly larger than the reduced density effect. Interestingly, given the strong DR in the RS case, it is clear that wall roughness does not necessarily prevent strong bubble drag reduction. In fact, ribs in the RS case have a similar effect on the flow as cavitators used in air cavity DR (Zverkhovskyi Reference Zverkhovskyi2014; Verschoof et al.
Reference Verschoof, Bakhuis, Bullee, Huisman, Sun and Lohse2018). The ribs create a low pressure region in the wake, attracting air to form an air layer. In the RS case, both bubble DR and air cavity DR contribute to the effective DR. For both the RS and SS cases, the drag reduction increases with Taylor number (van Gils et al.
Reference van Gils, Narezo Guzman, Sun and Lohse2013), contrasting the SR and RR cases, in which the drag reduction does not have a clear monotonic Taylor number dependence.
$\unicode[STIX]{x1D70C}_{air}$
is the air density. For the RS and SS cases, however, the drag reduction is significantly larger than the reduced density effect. Interestingly, given the strong DR in the RS case, it is clear that wall roughness does not necessarily prevent strong bubble drag reduction. In fact, ribs in the RS case have a similar effect on the flow as cavitators used in air cavity DR (Zverkhovskyi Reference Zverkhovskyi2014; Verschoof et al.
Reference Verschoof, Bakhuis, Bullee, Huisman, Sun and Lohse2018). The ribs create a low pressure region in the wake, attracting air to form an air layer. In the RS case, both bubble DR and air cavity DR contribute to the effective DR. For both the RS and SS cases, the drag reduction increases with Taylor number (van Gils et al.
Reference van Gils, Narezo Guzman, Sun and Lohse2013), contrasting the SR and RR cases, in which the drag reduction does not have a clear monotonic Taylor number dependence.

Figure 4. Instantaneous photographs of the flow for all four roughness cases: SS, RS, SR and RR. Clear differences in the flow patterns are visible. In the SS and RS cases, we see turbulent streaks, but no stable structures. Clear stable Taylor rolls are visible for the SR and RR cases. We indicate the position of the rolls with the dashed line and the roll pairs with the dotted line. The Taylor number is
![]() $Ta=1.5\times 10^{12}$
, except for the RR case (
$Ta=1.5\times 10^{12}$
, except for the RR case (
![]() $Ta=8.4\times 10^{11}$
), while the outer cylinder is kept stationary. The void fraction in all cases is
$Ta=8.4\times 10^{11}$
), while the outer cylinder is kept stationary. The void fraction in all cases is
![]() $\unicode[STIX]{x1D6FC}=6\,\%$
. Note that in all cases the bubbles are not homogeneously distributed over the height; this is most visible in the SS case.
$\unicode[STIX]{x1D6FC}=6\,\%$
. Note that in all cases the bubbles are not homogeneously distributed over the height; this is most visible in the SS case.
To better understand the flow dynamics, we visualize the flow for a void fraction of
![]() $\unicode[STIX]{x1D6FC}=6\,\%$
. As shown in figure 4, for all four cases the flow structures are significantly different. In the SS and RS cases, clear streaks and patterns are visualized by the bubbles, but stable turbulent Taylor vortices are not observed. For both cases with ribs on the outer cylinder, i.e. the SR and RR cases, we do however observe stable turbulent Taylor vortices.
$\unicode[STIX]{x1D6FC}=6\,\%$
. As shown in figure 4, for all four cases the flow structures are significantly different. In the SS and RS cases, clear streaks and patterns are visualized by the bubbles, but stable turbulent Taylor vortices are not observed. For both cases with ribs on the outer cylinder, i.e. the SR and RR cases, we do however observe stable turbulent Taylor vortices.
The existence and the dynamics of Taylor vortices have been studied extensively for the single-phase smooth-wall case (Lathrop, Fineberg & Swinney Reference Lathrop, Fineberg and Swinney1992a
,Reference Lathrop, Fineberg and Swinney
b
; Lewis & Swinney Reference Lewis and Swinney1999; Huisman et al.
Reference Huisman, van der Veen, Sun and Lohse2014; Grossmann et al.
Reference Grossmann, Lohse and Sun2016; van der Veen et al.
Reference van der Veen, Huisman, Dung, Tang, Sun and Lohse2016). In the explored Taylor number regime, measurements showed that for sufficiently strong turbulence (
![]() $Re_{i}>10^{5}$
), stable Taylor rolls do not exist in the pure inner cylinder rotation regime, and are only present in the counter-rotating regime (Ostilla-Mónico et al.
Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014; Grossmann et al.
Reference Grossmann, Lohse and Sun2016). Roughness elements promote the ejection of turbulent plumes, leading to localized radial flows towards the outer cylinder (Zhu et al.
Reference Zhu, Ostilla-Monico, Verzicco and Lohse2016; Toppaladoddi, Succi & Wettlaufer Reference Toppaladoddi, Succi and Wettlaufer2017). As the TC system is closed, consequently a radial flow towards the inner cylinder must be present. These flows can organize themselves as stable Taylor rolls. Thus, as the roughness promotes the ejection of turbulent plumes, the existence of Taylor vortices is stimulated.
$Re_{i}>10^{5}$
), stable Taylor rolls do not exist in the pure inner cylinder rotation regime, and are only present in the counter-rotating regime (Ostilla-Mónico et al.
Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014; Grossmann et al.
Reference Grossmann, Lohse and Sun2016). Roughness elements promote the ejection of turbulent plumes, leading to localized radial flows towards the outer cylinder (Zhu et al.
Reference Zhu, Ostilla-Monico, Verzicco and Lohse2016; Toppaladoddi, Succi & Wettlaufer Reference Toppaladoddi, Succi and Wettlaufer2017). As the TC system is closed, consequently a radial flow towards the inner cylinder must be present. These flows can organize themselves as stable Taylor rolls. Thus, as the roughness promotes the ejection of turbulent plumes, the existence of Taylor vortices is stimulated.
The roll dynamics observed with wall roughness is different from what has been observed hitherto in the same set-up. Earlier studies found six or eight rolls for the smooth-wall case with counter-rotating cylinders (Huisman et al.
Reference Huisman, van der Veen, Sun and Lohse2014; van der Veen et al.
Reference van der Veen, Huisman, Dung, Tang, Sun and Lohse2016). Here, for pure inner cylinder rotation, we see ten rolls for the RR case, whereas for the SR case we observe eight rolls. The number of rolls is related to the aspect ratio
![]() $\unicode[STIX]{x1D6E4}$
, which depends on the gap width. The roughness elements decrease the ‘effective gap width’, and thus increase the apparent aspect ratio
$\unicode[STIX]{x1D6E4}$
, which depends on the gap width. The roughness elements decrease the ‘effective gap width’, and thus increase the apparent aspect ratio
![]() $\unicode[STIX]{x1D6E4}_{eff}$
, which is calculated by subtracting the rib height from the gap width. This results in aspect ratios of
$\unicode[STIX]{x1D6E4}_{eff}$
, which is calculated by subtracting the rib height from the gap width. This results in aspect ratios of
![]() $\unicode[STIX]{x1D6E4}_{SR,RS}=L/(d-h)=12.7$
and
$\unicode[STIX]{x1D6E4}_{SR,RS}=L/(d-h)=12.7$
and
![]() $\unicode[STIX]{x1D6E4}_{RR}=L/(d-2h)=13.8$
, whereas
$\unicode[STIX]{x1D6E4}_{RR}=L/(d-2h)=13.8$
, whereas
![]() $\unicode[STIX]{x1D6E4}=L/d=11.7$
. Consequently, the system allows for an increased number of rolls in the rough-wall cases. A roll aspect ratio can be defined as
$\unicode[STIX]{x1D6E4}=L/d=11.7$
. Consequently, the system allows for an increased number of rolls in the rough-wall cases. A roll aspect ratio can be defined as
![]() $AR=\unicode[STIX]{x1D6E4}/N_{r}$
, in which
$AR=\unicode[STIX]{x1D6E4}/N_{r}$
, in which
![]() $N_{r}$
is the number of rolls (Chouippe et al.
Reference Chouippe, Climent, Legendre and Gabillet2014; Huisman et al.
Reference Huisman, van der Veen, Sun and Lohse2014; van der Veen et al.
Reference van der Veen, Huisman, Dung, Tang, Sun and Lohse2016). With the current radius ratio, the smooth wall roll aspect ratios are found to be
$N_{r}$
is the number of rolls (Chouippe et al.
Reference Chouippe, Climent, Legendre and Gabillet2014; Huisman et al.
Reference Huisman, van der Veen, Sun and Lohse2014; van der Veen et al.
Reference van der Veen, Huisman, Dung, Tang, Sun and Lohse2016). With the current radius ratio, the smooth wall roll aspect ratios are found to be
![]() $1.14\leqslant AR_{SS}\leqslant 1.96$
, with a value of
$1.14\leqslant AR_{SS}\leqslant 1.96$
, with a value of
![]() $AR_{SS}=1.46$
being most common in the currently used set-up. In the SR and RR cases, we observe eight and ten rolls, respectively, resulting in roll aspect ratios of
$AR_{SS}=1.46$
being most common in the currently used set-up. In the SR and RR cases, we observe eight and ten rolls, respectively, resulting in roll aspect ratios of
![]() $AR_{SR}=1.59$
and
$AR_{SR}=1.59$
and
![]() $AR_{RR}=1.38$
, respectively.
$AR_{RR}=1.38$
, respectively.
We argue that the existence of the Taylor vortices is the underlying mechanism through which the effectiveness of bubble drag reduction is reduced in the SR and RR cases. The Taylor vortices have two significant effects on the air: (i) the vortices enhance turbulent mixing of the flow, and (ii) the vortices attract air to the vortex core, as the local pressure in the core of the Taylor vortices is low. To effectively decrease the drag, it is crucial that large bubbles are present in or close to the boundary layer (van Gils et al. Reference van Gils, Narezo Guzman, Sun and Lohse2013; Verschoof et al. Reference Verschoof, van der Veen, Sun and Lohse2016; Spandan et al. Reference Spandan, Verzicco and Lohse2017). The flow visualizations show that the bubbles are dragged away from the inner cylinder wall, and are radially more mixed. Therefore, as the bubbles do not accumulate close to the inner cylinder, the drag reduction almost vanishes, and becomes close to the trivial effect of the reduced global effective density, as was shown in our torque measurements.

Figure 5. (a–d) Dimensionless torque as a function of rotation ratio
![]() $a$
for the roughness cases SS, SR, RS and RR with and without air. The Taylor number is kept constant at
$a$
for the roughness cases SS, SR, RS and RR with and without air. The Taylor number is kept constant at
![]() $Ta=7.3\times 10^{11}$
. We compensate
$Ta=7.3\times 10^{11}$
. We compensate
![]() $Nu_{\unicode[STIX]{x1D714}}$
by
$Nu_{\unicode[STIX]{x1D714}}$
by
![]() $Ta^{0.5}$
to remove viscosity changes due to temperature fluctuations, similar to Huisman et al. (Reference Huisman, van der Veen, Sun and Lohse2014). (e) Resulting drag reduction as a function of rotation ratio
$Ta^{0.5}$
to remove viscosity changes due to temperature fluctuations, similar to Huisman et al. (Reference Huisman, van der Veen, Sun and Lohse2014). (e) Resulting drag reduction as a function of rotation ratio
![]() $a$
, calculated here as
$a$
, calculated here as
![]() $\text{DR}=1-[Nu_{\unicode[STIX]{x1D714}}Ta^{-0.4}(\unicode[STIX]{x1D6FC}=6\,\%)]/[Nu_{\unicode[STIX]{x1D714}}Ta^{-0.4}(\unicode[STIX]{x1D6FC}=0\,\%)]$
. The rotation ratio was increased from
$\text{DR}=1-[Nu_{\unicode[STIX]{x1D714}}Ta^{-0.4}(\unicode[STIX]{x1D6FC}=6\,\%)]/[Nu_{\unicode[STIX]{x1D714}}Ta^{-0.4}(\unicode[STIX]{x1D6FC}=0\,\%)]$
. The rotation ratio was increased from
![]() $a=0$
to
$a=0$
to
![]() $a=1$
in a single, continuous quasi-static measurement. For figure (b), we binned the results using 40 linearly distributed bins. Typical error bars are shown.
$a=1$
in a single, continuous quasi-static measurement. For figure (b), we binned the results using 40 linearly distributed bins. Typical error bars are shown.
Up to here, we showed that in the SR and RR cases, the ribs induce turbulent Taylor vortices, and we argued that Taylor rolls eliminate DR. One could presume that the rolls, instead of being the underlying physical explanation, merely coincide with the weak DR. To further prove the effect of turbulent Taylor vortices on bubble DR, we study the DR behaviour in the counter-rotation regime. For the SS case, pronounced stable turbulent Taylor vortices exist in the counter-rotating regime within approximately
![]() $0.1\leqslant a\leqslant 0.5$
(van Gils et al.
Reference van Gils, Huisman, Grossmann, Sun and Lohse2012; Huisman et al.
Reference Huisman, van der Veen, Sun and Lohse2014; van der Veen et al.
Reference van der Veen, Huisman, Dung, Tang, Sun and Lohse2016). By measuring the DR as a function of rotation ratio
$0.1\leqslant a\leqslant 0.5$
(van Gils et al.
Reference van Gils, Huisman, Grossmann, Sun and Lohse2012; Huisman et al.
Reference Huisman, van der Veen, Sun and Lohse2014; van der Veen et al.
Reference van der Veen, Huisman, Dung, Tang, Sun and Lohse2016). By measuring the DR as a function of rotation ratio
![]() $a=-\unicode[STIX]{x1D714}_{o}/\unicode[STIX]{x1D714}_{i}$
while keeping the Taylor number constant, we can directly show the influence of Taylor rolls on the effectiveness of air lubrication. For all roughness cases, we show the torque in figure 5(a–d) and the resulting DR in figure 5(e). As already shown before, we observe strong DR for the SS and SR cases at
$a=-\unicode[STIX]{x1D714}_{o}/\unicode[STIX]{x1D714}_{i}$
while keeping the Taylor number constant, we can directly show the influence of Taylor rolls on the effectiveness of air lubrication. For all roughness cases, we show the torque in figure 5(a–d) and the resulting DR in figure 5(e). As already shown before, we observe strong DR for the SS and SR cases at
![]() $a=0$
. Then, for increasing
$a=0$
. Then, for increasing
![]() $a$
, we see that the DR decreases. The observation is very similar to the previously discussed weak DR in the SR and RR cases, namely in the counter-rotating regime the bubbles are trapped in the Taylor rolls, dragged away from the boundary layer and unable to effectively decrease the drag. For the SR case, the strength of the turbulent Taylor vortices decreases with increasing outer cylinder. Consequently, an increase in DR is observed. For the RR case, the DR remains weak for all cases, as the turbulent Taylor vortices exist for the entire scanned parameter space.
$a$
, we see that the DR decreases. The observation is very similar to the previously discussed weak DR in the SR and RR cases, namely in the counter-rotating regime the bubbles are trapped in the Taylor rolls, dragged away from the boundary layer and unable to effectively decrease the drag. For the SR case, the strength of the turbulent Taylor vortices decreases with increasing outer cylinder. Consequently, an increase in DR is observed. For the RR case, the DR remains weak for all cases, as the turbulent Taylor vortices exist for the entire scanned parameter space.
4 Conclusions
To conclude, we studied the influence of wall roughness on bubble drag reduction in a highly turbulent flow. We showed that in the SR and RR cases wall roughness promotes stable turbulent Taylor rolls, which induce strong secondary flows, suppressing the drag reduction. Bubbles are captured in low vorticity regions, and therefore dragged away from the inner cylinder boundary layer. As a result, the drag reduction is mostly lost, and the effective drag reduction is close to the trivial effect of reduced global density. These findings help us to understand earlier studies on air lubrication and wall roughness, which had conflicting results as to whether roughness influences bubble drag reduction. We here distinguish two different regimes: (i) a regime with strong drag reduction if the roughness does not introduce strong secondary flows, and (ii) a regime with weak drag reduction if strong secondary flows are induced by the roughness.
Future work will include studies on wall roughness combined with bubbles in other types of set-ups, e.g. flat plates, or pipe flow. In these set-ups, roughness increases the velocity fluctuations but does not necessarily induce stable large-scale secondary flows, and thus the bubble DR behaviour might be significantly different from that in the current study. Moreover, as we limited ourselves to the influence of rib roughness, more work is needed to understand the influence of more realistic types of roughness.
Acknowledgements
We thank Tom van Terwisga (MARIN, TU Delft) for the continuous and stimulating collaboration over the years on drag reduction in the marine context. We also thank Dennis van Gils, Gert-Wim Bruggert and Martin Bos for their technical support. The work was financially supported by NWO-TTW (project 13265). We acknowledge support from EuHIT and MCEC. C.S. and D.B. acknowledge financial support from VIDI grant no. 13477, and the Natural Science Foundation of China under grant no. 11672156. P.A.B acknowledges NWO-TTW (project 14504).