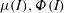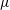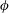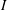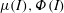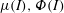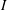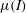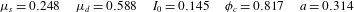1 Introduction
The original incompressible
![]() $\unicode[STIX]{x1D707}(I)$
-rheology was proposed (GDR MiDi 2004; Jop, Forterre & Pouliquen Reference Jop, Forterre and Pouliquen2006) to describe granular flow in which the particles are rigid and the solids volume fraction
$\unicode[STIX]{x1D707}(I)$
-rheology was proposed (GDR MiDi 2004; Jop, Forterre & Pouliquen Reference Jop, Forterre and Pouliquen2006) to describe granular flow in which the particles are rigid and the solids volume fraction
![]() $\unicode[STIX]{x1D719}$
is constant and uniform. The key physical insight behind the theory was that, under these circumstances, the only non-dimensional groups are the bulk friction coefficient
$\unicode[STIX]{x1D719}$
is constant and uniform. The key physical insight behind the theory was that, under these circumstances, the only non-dimensional groups are the bulk friction coefficient
![]() $\unicode[STIX]{x1D707}$
(the ratio
$\unicode[STIX]{x1D707}$
(the ratio
![]() $\unicode[STIX]{x1D70F}/p$
of shear stress to pressure) and the inertial number
$\unicode[STIX]{x1D70F}/p$
of shear stress to pressure) and the inertial number
where
![]() $d$
is the grain diameter,
$d$
is the grain diameter,
![]() $\dot{\unicode[STIX]{x1D6FE}}$
is the shear rate,
$\dot{\unicode[STIX]{x1D6FE}}$
is the shear rate,
![]() $p$
is the pressure and
$p$
is the pressure and
![]() $\unicode[STIX]{x1D70C}_{\ast }$
is the intrinsic grain density. When forming a constitutive law from these groups, dimensionless analysis implies that one group must be a function of the other, i.e.
$\unicode[STIX]{x1D70C}_{\ast }$
is the intrinsic grain density. When forming a constitutive law from these groups, dimensionless analysis implies that one group must be a function of the other, i.e.
This approach has led to significant progress in modelling granular flows (e.g. Lagrée, Staron & Popinet Reference Lagrée, Staron and Popinet2011; Staron, Lagrée & Popinet Reference Staron, Lagrée and Popinet2012; Gray & Edwards Reference Gray and Edwards2014; Barker & Gray Reference Barker and Gray2017). However, Barker et al. (Reference Barker, Schaeffer, Bohorquez and Gray2015) identified conditions on
![]() $\unicode[STIX]{x1D707}(I)$
and
$\unicode[STIX]{x1D707}(I)$
and
![]() $I$
under which incompressible
$I$
under which incompressible
![]() $\unicode[STIX]{x1D707}(I)$
-rheology is ill-posed.
$\unicode[STIX]{x1D707}(I)$
-rheology is ill-posed.
In reality granular flow is compressible and the solids volume fraction
![]() $\unicode[STIX]{x1D719}$
may vary. With compressibility there are multiple non-dimensional groups, which greatly complicates the possible rheology. Nevertheless, GDR MiDi (2004), da Cruz et al. (Reference da Cruz, Emam, Prochnow, Roux and Chevoir2005) and Pouliquen et al. (Reference Pouliquen, Cassar, Jop, Forterre and Nicolas2006) found that, in steady-state simulations and experiments,
$\unicode[STIX]{x1D719}$
may vary. With compressibility there are multiple non-dimensional groups, which greatly complicates the possible rheology. Nevertheless, GDR MiDi (2004), da Cruz et al. (Reference da Cruz, Emam, Prochnow, Roux and Chevoir2005) and Pouliquen et al. (Reference Pouliquen, Cassar, Jop, Forterre and Nicolas2006) found that, in steady-state simulations and experiments,
![]() $\unicode[STIX]{x1D719}$
depended on just the inertial number
$\unicode[STIX]{x1D719}$
depended on just the inertial number
where
![]() $\unicode[STIX]{x1D6F7}$
is a monotonically decreasing function of
$\unicode[STIX]{x1D6F7}$
is a monotonically decreasing function of
![]() $I$
. Note that (1.3) implies Bagnold scaling (Bagnold Reference Bagnold1954) for the pressure (i.e. it scales with the square of strain rate). Specifically, if
$I$
. Note that (1.3) implies Bagnold scaling (Bagnold Reference Bagnold1954) for the pressure (i.e. it scales with the square of strain rate). Specifically, if
![]() $\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D719})$
is the inverse function of
$\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D719})$
is the inverse function of
![]() $\unicode[STIX]{x1D6F7}(I)$
, then (1.1) may be rearranged to yield
$\unicode[STIX]{x1D6F7}(I)$
, then (1.1) may be rearranged to yield
This is consistent with the discrete element method (DEM) simulations of Chialvo, Sun & Sundaresan (Reference Chialvo, Sun and Sundaresan2012) in the inertial regime, in which the solids volume fraction
![]() $\unicode[STIX]{x1D719}$
is less than a critical volume fraction
$\unicode[STIX]{x1D719}$
is less than a critical volume fraction
![]() $\unicode[STIX]{x1D719}_{c}$
, namely the jamming point (Liu & Nagel Reference Liu and Nagel1998). For
$\unicode[STIX]{x1D719}_{c}$
, namely the jamming point (Liu & Nagel Reference Liu and Nagel1998). For
![]() $\unicode[STIX]{x1D719}>\unicode[STIX]{x1D719}_{c}$
, the stiffness of the particles becomes important and the rheology changes to either a ‘quasi-static’ or an ‘intermediate’ regime, which both depart from the Bagnold scaling. In general, the critical volume fraction
$\unicode[STIX]{x1D719}>\unicode[STIX]{x1D719}_{c}$
, the stiffness of the particles becomes important and the rheology changes to either a ‘quasi-static’ or an ‘intermediate’ regime, which both depart from the Bagnold scaling. In general, the critical volume fraction
![]() $\unicode[STIX]{x1D719}_{c}$
is dependent on the polydispersity of the grain-size distribution as well as the interparticle friction.
$\unicode[STIX]{x1D719}_{c}$
is dependent on the polydispersity of the grain-size distribution as well as the interparticle friction.
These observations led to the compressible
![]() $\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology (GDR MiDi 2004; Pouliquen et al.
Reference Pouliquen, Cassar, Jop, Forterre and Nicolas2006; Forterre & Pouliquen Reference Forterre and Pouliquen2008) in which the scalar relation (1.3), as well as (1.2), is assumed to hold even in non-steady situations. Although it might seem that compressibility would reduce the tendency to ill-posedness, in fact the compressible
$\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology (GDR MiDi 2004; Pouliquen et al.
Reference Pouliquen, Cassar, Jop, Forterre and Nicolas2006; Forterre & Pouliquen Reference Forterre and Pouliquen2008) in which the scalar relation (1.3), as well as (1.2), is assumed to hold even in non-steady situations. Although it might seem that compressibility would reduce the tendency to ill-posedness, in fact the compressible
![]() $\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology is even more prone to ill-posedness in time-dependent calculations than incompressible
$\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology is even more prone to ill-posedness in time-dependent calculations than incompressible
![]() $\unicode[STIX]{x1D707}(I)$
-rheology (Heyman et al.
Reference Heyman, Delannay, Tabuteau and Valance2017). Such instability is perhaps not surprising since the equations are not always dissipative (see appendix B). To demonstrate this ill-posedness, § 3 presents computations for a one-dimensional gravity-free shear cell in which the
$\unicode[STIX]{x1D707}(I)$
-rheology (Heyman et al.
Reference Heyman, Delannay, Tabuteau and Valance2017). Such instability is perhaps not surprising since the equations are not always dissipative (see appendix B). To demonstrate this ill-posedness, § 3 presents computations for a one-dimensional gravity-free shear cell in which the
![]() $\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology blows up catastrophically once the mesh size is refined sufficiently, even though the initial conditions are just a small perturbation of the steady solution.
$\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology blows up catastrophically once the mesh size is refined sufficiently, even though the initial conditions are just a small perturbation of the steady solution.
The purpose of this paper is to develop a viable alternative to
![]() $\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology that preserves its successes. This alternative is based on the compressible
$\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology that preserves its successes. This alternative is based on the compressible
![]() $I$
-dependent rheology (CIDR) introduced recently in Barker et al. (Reference Barker, Schaeffer, Shearer and Gray2017). After briefly recalling the general formulation of CIDR, specific yield and dilatancy functions are introduced, which ensure that the theory is well-posed and reduces to
$I$
-dependent rheology (CIDR) introduced recently in Barker et al. (Reference Barker, Schaeffer, Shearer and Gray2017). After briefly recalling the general formulation of CIDR, specific yield and dilatancy functions are introduced, which ensure that the theory is well-posed and reduces to
![]() $\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology in the correct limits. Specifically, the new inertial CIDR equations recover both the
$\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology in the correct limits. Specifically, the new inertial CIDR equations recover both the
![]() $\unicode[STIX]{x1D707}(I)$
and
$\unicode[STIX]{x1D707}(I)$
and
![]() $\unicode[STIX]{x1D6F7}(I)$
relations (1.2)–(1.3) when the flow is isochoric (
$\unicode[STIX]{x1D6F7}(I)$
relations (1.2)–(1.3) when the flow is isochoric (
![]() $\text{div}\,\boldsymbol{u}=0$
), which in many geometries corresponds to steady flow. Sample computations with the one-dimensional inertial CIDR equations in a gravity-free shear cell converge to the steady-state solution, even for initial conditions that are a long way from steady state. Moreover, these computations agree well with transient DEM simulations of the same flows.
$\text{div}\,\boldsymbol{u}=0$
), which in many geometries corresponds to steady flow. Sample computations with the one-dimensional inertial CIDR equations in a gravity-free shear cell converge to the steady-state solution, even for initial conditions that are a long way from steady state. Moreover, these computations agree well with transient DEM simulations of the same flows.
In §§ 2 and 3 the
![]() $\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology is described and computations that blow up because of ill-posedness are presented. Sections 4 and 5 introduce CIDR for the inertial regime and show that computations converge to steady state, and these computations are supported by DEM simulations described in § 6. The final two sections discuss a number of related issues and summarize the overall conclusions. Appendix A derives conditions for ill-posedness of the one-dimensional
$\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology is described and computations that blow up because of ill-posedness are presented. Sections 4 and 5 introduce CIDR for the inertial regime and show that computations converge to steady state, and these computations are supported by DEM simulations described in § 6. The final two sections discuss a number of related issues and summarize the overall conclusions. Appendix A derives conditions for ill-posedness of the one-dimensional
![]() $\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology in a gravity-free shear cell, appendix B relates the CIDR equations to the thermodynamic analysis of Goddard & Lee (Reference Goddard and Lee2018) and appendix C describes the formulation of the DEM simulations.
$\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology in a gravity-free shear cell, appendix B relates the CIDR equations to the thermodynamic analysis of Goddard & Lee (Reference Goddard and Lee2018) and appendix C describes the formulation of the DEM simulations.
2 The
 $\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology for granular flows
$\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology for granular flows
In a continuum formulation, dense granular flow is described by the solids fraction
![]() $\unicode[STIX]{x1D719}$
, the velocity vector
$\unicode[STIX]{x1D719}$
, the velocity vector
![]() $\boldsymbol{u}$
and the symmetric Cauchy stress tensor
$\boldsymbol{u}$
and the symmetric Cauchy stress tensor
![]() $\unicode[STIX]{x1D748}$
. In two dimensions (to which this paper is restricted) this formulation constitutes six scalar unknown functions of position and time. These satisfy governing equations including three conservation laws: one for conservation of mass
$\unicode[STIX]{x1D748}$
. In two dimensions (to which this paper is restricted) this formulation constitutes six scalar unknown functions of position and time. These satisfy governing equations including three conservation laws: one for conservation of mass
and two momentum conservation laws
where
![]() $\unicode[STIX]{x1D70C}_{\ast }$
is the intrinsic density of the grains and body forces have been neglected. In addition to the three conservation laws, three constitutive relations are needed to close this system.
$\unicode[STIX]{x1D70C}_{\ast }$
is the intrinsic density of the grains and body forces have been neglected. In addition to the three conservation laws, three constitutive relations are needed to close this system.
To write these constitutive laws, it is convenient to decompose the stress tensor into a pressure term
![]() $p=-\unicode[STIX]{x1D70E}_{ii}/2$
plus a trace-free tensor
$p=-\unicode[STIX]{x1D70E}_{ii}/2$
plus a trace-free tensor
![]() $\unicode[STIX]{x1D749}$
, called the shear-stress tensor or the deviatoric stress tensor, such that
$\unicode[STIX]{x1D749}$
, called the shear-stress tensor or the deviatoric stress tensor, such that
The constitutive law for the incompressible
![]() $\unicode[STIX]{x1D707}(I)$
-rheology (Jop et al.
Reference Jop, Forterre and Pouliquen2006; Forterre & Pouliquen Reference Forterre and Pouliquen2008; Barker et al.
Reference Barker, Schaeffer, Bohorquez and Gray2015) is formulated in terms of the (total) strain-rate tensor
$\unicode[STIX]{x1D707}(I)$
-rheology (Jop et al.
Reference Jop, Forterre and Pouliquen2006; Forterre & Pouliquen Reference Forterre and Pouliquen2008; Barker et al.
Reference Barker, Schaeffer, Bohorquez and Gray2015) is formulated in terms of the (total) strain-rate tensor
but for the compressible generalizations of the
![]() $\unicode[STIX]{x1D707}(I)$
-rheology (GDR MiDi 2004; Pouliquen et al.
Reference Pouliquen, Cassar, Jop, Forterre and Nicolas2006; Forterre & Pouliquen Reference Forterre and Pouliquen2008; Barker et al.
Reference Barker, Schaeffer, Shearer and Gray2017; Heyman et al.
Reference Heyman, Delannay, Tabuteau and Valance2017; Goddard & Lee Reference Goddard and Lee2018) it is also useful to define the deviatoric strain-rate tensor
$\unicode[STIX]{x1D707}(I)$
-rheology (GDR MiDi 2004; Pouliquen et al.
Reference Pouliquen, Cassar, Jop, Forterre and Nicolas2006; Forterre & Pouliquen Reference Forterre and Pouliquen2008; Barker et al.
Reference Barker, Schaeffer, Shearer and Gray2017; Heyman et al.
Reference Heyman, Delannay, Tabuteau and Valance2017; Goddard & Lee Reference Goddard and Lee2018) it is also useful to define the deviatoric strain-rate tensor
where
![]() $\unicode[STIX]{x1D61A}_{ij}$
is trace free. The alignment constitutive law, which is imposed in both
$\unicode[STIX]{x1D61A}_{ij}$
is trace free. The alignment constitutive law, which is imposed in both
![]() $\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology and CIDR, states that
$\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology and CIDR, states that
where the notation
![]() $\Vert \unicode[STIX]{x1D64F}\Vert =\sqrt{\text{tr}(\unicode[STIX]{x1D64F}^{2})/2}$
denotes the second invariant of any symmetric tensor
$\Vert \unicode[STIX]{x1D64F}\Vert =\sqrt{\text{tr}(\unicode[STIX]{x1D64F}^{2})/2}$
denotes the second invariant of any symmetric tensor
![]() $\unicode[STIX]{x1D64F}$
. In particular, the eigenvectors of the deviatoric stress tensor and the deviatoric strain-rate tensor are parallel. This matrix equation is in fact equivalent to just one scalar equation and relies upon the implicit assumption that
$\unicode[STIX]{x1D64F}$
. In particular, the eigenvectors of the deviatoric stress tensor and the deviatoric strain-rate tensor are parallel. This matrix equation is in fact equivalent to just one scalar equation and relies upon the implicit assumption that
![]() $\Vert \unicode[STIX]{x1D64E}\Vert \neq 0$
; i.e. that material is actually shearing. The other two constitutive laws in the
$\Vert \unicode[STIX]{x1D64E}\Vert \neq 0$
; i.e. that material is actually shearing. The other two constitutive laws in the
![]() $\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology specify the deviatoric stress
$\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology specify the deviatoric stress
![]() $\unicode[STIX]{x1D70F}=\Vert \unicode[STIX]{x1D749}\Vert$
and the solids fraction
$\unicode[STIX]{x1D70F}=\Vert \unicode[STIX]{x1D749}\Vert$
and the solids fraction
![]() $\unicode[STIX]{x1D719}$
:
$\unicode[STIX]{x1D719}$
:
in terms of the pressure
![]() $p$
and the inertial number
$p$
and the inertial number
where
![]() $\unicode[STIX]{x1D707}(I)$
is the bulk friction coefficient and
$\unicode[STIX]{x1D707}(I)$
is the bulk friction coefficient and
![]() $d$
is the grain diameter.
$d$
is the grain diameter.
The constitutive laws (2.6)–(2.8) are referred to as
![]() $\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology. Commonly used functional forms for
$\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology. Commonly used functional forms for
![]() $\unicode[STIX]{x1D707}(I)$
and
$\unicode[STIX]{x1D707}(I)$
and
![]() $\unicode[STIX]{x1D6F7}(I)$
in the constitutive laws (2.7) and (2.8) are
$\unicode[STIX]{x1D6F7}(I)$
in the constitutive laws (2.7) and (2.8) are
where
![]() $\unicode[STIX]{x1D707}_{s}$
,
$\unicode[STIX]{x1D707}_{s}$
,
![]() $\unicode[STIX]{x1D707}_{d}$
,
$\unicode[STIX]{x1D707}_{d}$
,
![]() $I_{0}$
,
$I_{0}$
,
![]() $\unicode[STIX]{x1D719}_{c}$
and
$\unicode[STIX]{x1D719}_{c}$
and
![]() $a$
are constant material parameters (GDR MiDi 2004; Jop et al.
Reference Jop, Forterre and Pouliquen2006; Forterre & Pouliquen Reference Forterre and Pouliquen2008; Trulsson et al.
Reference Trulsson, Bouzid, Claudin and Andreotti2013). As shown in figure 1, these functions provide a good fit for the DEM simulations performed in this paper (see appendix C). Table 1 lists the best-fit parameters extracted from the steady-state DEM simulations. Note that figure 1 includes data for multiple cases with differing particle stiffness and system size, which shows that the parameters do not depend on the details of the DEM simulations.
$a$
are constant material parameters (GDR MiDi 2004; Jop et al.
Reference Jop, Forterre and Pouliquen2006; Forterre & Pouliquen Reference Forterre and Pouliquen2008; Trulsson et al.
Reference Trulsson, Bouzid, Claudin and Andreotti2013). As shown in figure 1, these functions provide a good fit for the DEM simulations performed in this paper (see appendix C). Table 1 lists the best-fit parameters extracted from the steady-state DEM simulations. Note that figure 1 includes data for multiple cases with differing particle stiffness and system size, which shows that the parameters do not depend on the details of the DEM simulations.
Incidentally the form
![]() $\unicode[STIX]{x1D6F7}(I)=\unicode[STIX]{x1D719}_{c}-(\unicode[STIX]{x1D719}_{c}-\unicode[STIX]{x1D719}_{min})/(I_{\ast }/I+1)$
, where
$\unicode[STIX]{x1D6F7}(I)=\unicode[STIX]{x1D719}_{c}-(\unicode[STIX]{x1D719}_{c}-\unicode[STIX]{x1D719}_{min})/(I_{\ast }/I+1)$
, where
![]() $\unicode[STIX]{x1D719}_{min}$
and
$\unicode[STIX]{x1D719}_{min}$
and
![]() $I_{\ast }$
are constants, might be preferable to (2.11), which becomes negative for large
$I_{\ast }$
are constants, might be preferable to (2.11), which becomes negative for large
![]() $I$
. However, the simpler form (2.11) is adequate for most practical purposes, because
$I$
. However, the simpler form (2.11) is adequate for most practical purposes, because
![]() $I$
rarely becomes large enough to drive
$I$
rarely becomes large enough to drive
![]() $\unicode[STIX]{x1D6F7}(I)$
negative.
$\unicode[STIX]{x1D6F7}(I)$
negative.
Since (2.11) is a monotonically decreasing function, equation (2.8) can be inverted to write the inertial number as a function of the solids volume fraction
which, for the specific function (2.11) used here, gives
From this it is also possible to determine an equation of state for the pressure by substituting (2.12) into the inertial number (2.9) and solving for
![]() $p$
to give
$p$
to give
which, for fixed
![]() $\unicode[STIX]{x1D719}$
, exhibits the Bagnold scaling in that the pressure scales with the square of strain rate as in (1.4). Note that this pressure tends to infinity as
$\unicode[STIX]{x1D719}$
, exhibits the Bagnold scaling in that the pressure scales with the square of strain rate as in (1.4). Note that this pressure tends to infinity as
![]() $\unicode[STIX]{x1D719}\rightarrow \unicode[STIX]{x1D719}_{c}$
, behaviour that is discussed in § 7.2.
$\unicode[STIX]{x1D719}\rightarrow \unicode[STIX]{x1D719}_{c}$
, behaviour that is discussed in § 7.2.

Figure 1. Steady-state relations for (a) the bulk friction coefficient
![]() $\unicode[STIX]{x1D707}$
and (b) the solids volume fraction
$\unicode[STIX]{x1D707}$
and (b) the solids volume fraction
![]() $\unicode[STIX]{x1D719}$
as functions of the inertial number
$\unicode[STIX]{x1D719}$
as functions of the inertial number
![]() $I$
. Solid blue lines are the functional forms (2.10) and (2.11) evaluated with the parameters in table 1. Symbols are the results of multiple DEM simulations (see appendix C for details) in which the normal spring constant
$I$
. Solid blue lines are the functional forms (2.10) and (2.11) evaluated with the parameters in table 1. Symbols are the results of multiple DEM simulations (see appendix C for details) in which the normal spring constant
![]() $k^{(n)}$
, the cell height
$k^{(n)}$
, the cell height
![]() $H$
and number of particles
$H$
and number of particles
![]() $N$
have been varied.
$N$
have been varied.
3 Catastrophic failure with the
 $\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology
$\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology
As mentioned in the introduction, it follows from Heyman et al. (Reference Heyman, Delannay, Tabuteau and Valance2017) that the dynamic equations of
![]() $\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology for two-dimensional flow are always ill-posed. In this section it is demonstrated that ill-posedness can contaminate even the simplest of problems: flow in a two-dimensional shear cell that depends on only one spatial variable.
$\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology for two-dimensional flow are always ill-posed. In this section it is demonstrated that ill-posedness can contaminate even the simplest of problems: flow in a two-dimensional shear cell that depends on only one spatial variable.
3.1 Equations for one-dimensional flow in a shear cell
In a planar shear cell granular material is confined from above and below by two parallel flat frictional walls, whose relative motion, in the absence of gravity, provides the only driving for the flow. This is a popular idealized geometry for the study of granular rheology, and the set-up can be either volume controlled, by fixing the wall separation distance
![]() $H$
, or pressure controlled, by applying a normal force at the walls. In the following investigations
$H$
, or pressure controlled, by applying a normal force at the walls. In the following investigations
![]() $H$
will be fixed and solutions will be restricted to those which are invariant in the shearing direction
$H$
will be fixed and solutions will be restricted to those which are invariant in the shearing direction
![]() $x$
and depend only on the vertical coordinate
$x$
and depend only on the vertical coordinate
![]() $z$
and time. As such, this reduces the two-dimensional problem to one spatial dimension in the interval
$z$
and time. As such, this reduces the two-dimensional problem to one spatial dimension in the interval
![]() $0<z<H$
. As the flow is taken to be compressible, both components of the velocity
$0<z<H$
. As the flow is taken to be compressible, both components of the velocity
![]() $\boldsymbol{u}=(u,w)$
may be non-zero and depend on
$\boldsymbol{u}=(u,w)$
may be non-zero and depend on
![]() $z$
and
$z$
and
![]() $t$
. For this special class of flows, the conservation laws (2.1)–(2.2) simplify to
$t$
. For this special class of flows, the conservation laws (2.1)–(2.2) simplify to
since all
![]() $x$
-derivatives vanish. In addition, the deviatoric strain rate reduces to
$x$
-derivatives vanish. In addition, the deviatoric strain rate reduces to
and its second invariant becomes
It follows that in the shear cell the equation of state (2.14) reduces to
which provides an explicit expression for the pressure.
The alignment condition (2.6) implies that the relevant components of the deviatoric stress are
which using the constitutive law (2.7) and equations (3.5) and (2.12) implies
Equations (3.6) and (3.8) may then be substituted into the conservation laws (3.1)–(3.3) to obtain a system of three partial differential equations (PDEs) for
![]() $\unicode[STIX]{x1D719}$
,
$\unicode[STIX]{x1D719}$
,
![]() $u$
and
$u$
and
![]() $w$
that are first order in time and second order in space.
$w$
that are first order in time and second order in space.
For a given set of initial conditions
![]() $\unicode[STIX]{x1D719}(z,0)$
,
$\unicode[STIX]{x1D719}(z,0)$
,
![]() $u(z,0)$
,
$u(z,0)$
,
![]() $w(z,0)$
the three PDEs must be solved subject to the boundary conditions that there is no slip at the walls
$w(z,0)$
the three PDEs must be solved subject to the boundary conditions that there is no slip at the walls
where
![]() $V_{0}$
is the velocity of the top wall. It is easily verified that the steady linear shearing solution
$V_{0}$
is the velocity of the top wall. It is easily verified that the steady linear shearing solution
where
![]() $\unicode[STIX]{x1D719}_{0}$
is the average initial solids volume fraction
$\unicode[STIX]{x1D719}_{0}$
is the average initial solids volume fraction
satisfies (3.1)–(3.3) given (3.6), (3.8) and the boundary conditions (3.9). It is therefore anticipated that any set of initial conditions will tend to this solution.
3.2 Blow up and grid dependence with the
 $\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology
$\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology
For one-dimensional flow in a shear cell, the physical variables are non-dimensionalized with the scalings
where the hats indicate non-dimensional variables. Equations (3.1)–(3.3) with the relations (3.6) and (3.8) therefore reduce to the non-dimensional system
where the grains size
![]() $d$
, the grain density
$d$
, the grain density
![]() $\unicode[STIX]{x1D70C}_{\ast }$
and the wall velocity
$\unicode[STIX]{x1D70C}_{\ast }$
and the wall velocity
![]() $V_{0}$
scale completely out of the system.
$V_{0}$
scale completely out of the system.
The conservation laws (3.13)–(3.15) are solved by the numerical method of lines (Schiesser Reference Schiesser2012). This method discretizes the spatial derivatives in the PDEs which generates a system of coupled ordinary differential equations. These are then integrated forward in time using MATLAB’s ODE15s routine. Two different methods are used to approximate the spatial derivatives: the first is a finite difference method using first-order differences, while the second method uses a Chebyshev spectral scheme (Canuto et al. Reference Canuto, Hussaini, Quarteroni and Zang1988; Trefethen Reference Trefethen2000).

Figure 2. Initial conditions used to illustrate the computational difficulties encountered with the
![]() $\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology. Panels (a–c) show the non-dimensional velocity components
$\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology. Panels (a–c) show the non-dimensional velocity components
![]() $\hat{u} (\hat{z},0)$
,
$\hat{u} (\hat{z},0)$
,
![]() ${\hat{w}}(\hat{z},0)$
and the packing fraction
${\hat{w}}(\hat{z},0)$
and the packing fraction
![]() $\unicode[STIX]{x1D719}(\hat{z},0)$
as a function of the non-dimensional vertical coordinate
$\unicode[STIX]{x1D719}(\hat{z},0)$
as a function of the non-dimensional vertical coordinate
![]() $\hat{z}$
, respectively, for the initial condition (3.16) with
$\hat{z}$
, respectively, for the initial condition (3.16) with
![]() $\unicode[STIX]{x1D719}_{0}=0.78$
,
$\unicode[STIX]{x1D719}_{0}=0.78$
,
![]() $\unicode[STIX]{x1D716}=0.05$
and
$\unicode[STIX]{x1D716}=0.05$
and
![]() ${\hat{H}}=30$
. Panel (d) shows a plot of the function
${\hat{H}}=30$
. Panel (d) shows a plot of the function
![]() $\unicode[STIX]{x1D712}(\hat{z})$
, defined in (A 18), which determines where the flow is well-posed (
$\unicode[STIX]{x1D712}(\hat{z})$
, defined in (A 18), which determines where the flow is well-posed (
![]() $\unicode[STIX]{x1D712}<0$
) or ill-posed (
$\unicode[STIX]{x1D712}<0$
) or ill-posed (
![]() $\unicode[STIX]{x1D712}>0$
).
$\unicode[STIX]{x1D712}>0$
).

Figure 3. Snapshots of the non-dimensional vertical velocity for the
![]() $\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology computed with the method of lines in (a) a high-resolution finite difference discretization (
$\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology computed with the method of lines in (a) a high-resolution finite difference discretization (
![]() $N_{z}=201$
), (b) a high-resolution Chebychev spectral discretization (
$N_{z}=201$
), (b) a high-resolution Chebychev spectral discretization (
![]() $N_{z}=201$
) and (c) a low-resolution finite difference discretization (
$N_{z}=201$
) and (c) a low-resolution finite difference discretization (
![]() $N_{z}=47$
). In each panel the initial condition of the vertical velocity (3.16) is shown with a dashed black line. Movies 1–3 show the full time evolution of all fields (
$N_{z}=47$
). In each panel the initial condition of the vertical velocity (3.16) is shown with a dashed black line. Movies 1–3 show the full time evolution of all fields (
![]() $\hat{u}$
,
$\hat{u}$
,
![]() ${\hat{w}}$
and
${\hat{w}}$
and
![]() $\unicode[STIX]{x1D719}$
) and are available in the online supplementary material at https://doi.org/10.1017/jfm.2019.476.
$\unicode[STIX]{x1D719}$
) and are available in the online supplementary material at https://doi.org/10.1017/jfm.2019.476.
The non-dimensional height of the cell
![]() ${\hat{H}}$
is chosen to equal 30 (i.e. the physical height of the cell is 30 grain diameters). The initial conditions are plotted in figure 2 and are identical to the non-dimensionalized steady solution except that the vertical velocity has a small smooth imperfection in the centre of the domain:
${\hat{H}}$
is chosen to equal 30 (i.e. the physical height of the cell is 30 grain diameters). The initial conditions are plotted in figure 2 and are identical to the non-dimensionalized steady solution except that the vertical velocity has a small smooth imperfection in the centre of the domain:
where
![]() $\unicode[STIX]{x1D716}$
is a small parameter. It should be noted that this form does not satisfy the boundary conditions exactly but does within numerical precision. Provided
$\unicode[STIX]{x1D716}$
is a small parameter. It should be noted that this form does not satisfy the boundary conditions exactly but does within numerical precision. Provided
![]() $\unicode[STIX]{x1D716}$
is not too small, the ill-posedness condition (A 19), outlined in appendix A, is satisfied in the centre of the domain, as shown in figure 2(d), and it is therefore anticipated that numerical problems will develop.
$\unicode[STIX]{x1D716}$
is not too small, the ill-posedness condition (A 19), outlined in appendix A, is satisfied in the centre of the domain, as shown in figure 2(d), and it is therefore anticipated that numerical problems will develop.

Figure 4. (a) A comparison of the temporal evolution of the maximum vertical velocity
![]() $|{\hat{w}}|$
for the numerical computations presented in figure 3. The computations use the method of lines with a finite difference (dashed lines) and a Chebyshev (solids lines) discretization at both high (red lines) and low (blue lines) spatial resolution. The time
$|{\hat{w}}|$
for the numerical computations presented in figure 3. The computations use the method of lines with a finite difference (dashed lines) and a Chebyshev (solids lines) discretization at both high (red lines) and low (blue lines) spatial resolution. The time
![]() $\hat{t}_{\ast }=0.01052$
at which the Chebyshev scheme becomes non-convergent is indicated. (b) The final time
$\hat{t}_{\ast }=0.01052$
at which the Chebyshev scheme becomes non-convergent is indicated. (b) The final time
![]() $\hat{t}_{\ast }$
before convergence failure is plotted for the Chebyshev spectral discretization as a function of the number of grid points
$\hat{t}_{\ast }$
before convergence failure is plotted for the Chebyshev spectral discretization as a function of the number of grid points
![]() $N_{z}$
. The same plot (not shown) for failure of the finite difference computation is qualitatively similar, but differs in detail.
$N_{z}$
. The same plot (not shown) for failure of the finite difference computation is qualitatively similar, but differs in detail.
Confirming this anticipation, various snapshots of the non-dimensional vertical velocity are shown in figure 3. (The full time evolutions of
![]() $\hat{u} (\hat{z},\hat{t})$
,
$\hat{u} (\hat{z},\hat{t})$
,
![]() ${\hat{w}}(\hat{z},\hat{t})$
and
${\hat{w}}(\hat{z},\hat{t})$
and
![]() $\unicode[STIX]{x1D719}(\hat{z},\hat{t})$
are shown in supplementary movies 1–3.) In the high-resolution plots (figure 3
a,b), the growth of noise causes the numerical method to break down at the indicated time – at this point integration tolerances can no longer be met. Note that the misbehaviour originates in the centre of the domain, where the ill-posedness condition (A 19) is satisfied. Moreover, although the two solutions blow up at similar times, their spatial structure is completely different.
$\unicode[STIX]{x1D719}(\hat{z},\hat{t})$
are shown in supplementary movies 1–3.) In the high-resolution plots (figure 3
a,b), the growth of noise causes the numerical method to break down at the indicated time – at this point integration tolerances can no longer be met. Note that the misbehaviour originates in the centre of the domain, where the ill-posedness condition (A 19) is satisfied. Moreover, although the two solutions blow up at similar times, their spatial structure is completely different.
In contrast, a low-resolution (
![]() $N_{z}=47$
) simulation using the finite difference scheme does not blow up and in fact decays towards the steady state, as shown in figures 3(c) and 4(a). (The same occurs for the low-resolution run with the Chebyshev spectral scheme (see figure 4
a).) This is exactly the behaviour that one might expect of a well-posed model, but here it is entirely due to the higher numerical diffusion in the low-resolution scheme. On grid refinement this diffusion is no longer sufficient to suppress the underlying ill-posedness of the equations, and instabilities develop.
$N_{z}=47$
) simulation using the finite difference scheme does not blow up and in fact decays towards the steady state, as shown in figures 3(c) and 4(a). (The same occurs for the low-resolution run with the Chebyshev spectral scheme (see figure 4
a).) This is exactly the behaviour that one might expect of a well-posed model, but here it is entirely due to the higher numerical diffusion in the low-resolution scheme. On grid refinement this diffusion is no longer sufficient to suppress the underlying ill-posedness of the equations, and instabilities develop.
For all values of
![]() $N_{z}$
above a certain threshold (see figure 4
b), the initial perturbation is amplified indefinitely, causing the method to fail. The time
$N_{z}$
above a certain threshold (see figure 4
b), the initial perturbation is amplified indefinitely, causing the method to fail. The time
![]() $\hat{t}_{\ast }$
at which the Chebyshev spectral discretization fails is plotted in figure 4(b) as a function of the number of grid points
$\hat{t}_{\ast }$
at which the Chebyshev spectral discretization fails is plotted in figure 4(b) as a function of the number of grid points
![]() $N_{z}$
. Higher spatial resolution computations resolve higher wavenumber instabilities that grow at a faster rate, leading to earlier failure.
$N_{z}$
. Higher spatial resolution computations resolve higher wavenumber instabilities that grow at a faster rate, leading to earlier failure.
4 Inertial compressible
 $I$
-dependent rheology (iCIDR)
$I$
-dependent rheology (iCIDR)
The CIDR is a general framework that retains the conservation laws (2.1)–(2.2) and the alignment condition (2.6), but it modifies the other two constitutive equations. The constitutive law for the deviatoric stress (2.7) is replaced by assuming that there is a yield condition such that, if material is deforming, then
where
![]() $Y$
is called the ‘yield function’. In addition, it is assumed that the density evolves dynamically according to a flow rule that is reminiscent of critical state soil mechanics (Schofield & Wroth Reference Schofield and Wroth1968; Jackson Reference Jackson and Meyer1983):
$Y$
is called the ‘yield function’. In addition, it is assumed that the density evolves dynamically according to a flow rule that is reminiscent of critical state soil mechanics (Schofield & Wroth Reference Schofield and Wroth1968; Jackson Reference Jackson and Meyer1983):
where
![]() $f$
is called the ‘dilatancy function’. Barker et al. (Reference Barker, Schaeffer, Shearer and Gray2017) showed that the CIDR equations are linearly well-posed provided the yield and dilatancy functions satisfy the following three conditions:
$f$
is called the ‘dilatancy function’. Barker et al. (Reference Barker, Schaeffer, Shearer and Gray2017) showed that the CIDR equations are linearly well-posed provided the yield and dilatancy functions satisfy the following three conditions:
A key result of this paper is the introduction of new constitutive functions which are motivated by the inertial regime. These are constructed to satisfy both the well-posedness conditions (4.3)–(4.5) and the observed asymptotic steady-state behaviour, known as the
![]() $\unicode[STIX]{x1D707}(I)$
and
$\unicode[STIX]{x1D707}(I)$
and
![]() $\unicode[STIX]{x1D6F7}(I)$
relations (1.2)–(1.3). These relationships are derived from isochoric (constant volume) flows in steady state (see figure 1 and appendix C). For the purpose of deriving
$\unicode[STIX]{x1D6F7}(I)$
relations (1.2)–(1.3). These relationships are derived from isochoric (constant volume) flows in steady state (see figure 1 and appendix C). For the purpose of deriving
![]() $Y$
and
$Y$
and
![]() $f$
they may be conveniently stated as follows:
$f$
they may be conveniently stated as follows:
where
![]() $\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D719})$
is the inverse function of
$\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D719})$
is the inverse function of
![]() $\unicode[STIX]{x1D6F7}(I)$
. Even with these constraints there are infinitely many possible choices for the yield function and dilatancy function. What might be described as the simplest acceptable choice for these functions is now proposed.
$\unicode[STIX]{x1D6F7}(I)$
. Even with these constraints there are infinitely many possible choices for the yield function and dilatancy function. What might be described as the simplest acceptable choice for these functions is now proposed.
The starting point for this new theory is the relation
![]() $Y=\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D719}))p$
in (4.6). However, this cannot lead to a well-posed theory as
$Y=\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D719}))p$
in (4.6). However, this cannot lead to a well-posed theory as
![]() $\unicode[STIX]{x2202}_{I}Y=0$
and thus (4.4) is not satisfied. Taking instead the simplest non-trivial
$\unicode[STIX]{x2202}_{I}Y=0$
and thus (4.4) is not satisfied. Taking instead the simplest non-trivial
![]() $I$
-dependence gives
$I$
-dependence gives
which reduces to the
![]() $\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology when
$\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology when
![]() $I=\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D719})$
. Figure 5 is a useful aid for comparing this formula with
$I=\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D719})$
. Figure 5 is a useful aid for comparing this formula with
![]() $\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology. The corresponding dilatancy function is then found through substitution of (4.7) into the well-posedness PDE (4.3). Taking contributions from both the homogeneous and particular solutions of (4.3) and imposing (4.6) gives the expression
$\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology. The corresponding dilatancy function is then found through substitution of (4.7) into the well-posedness PDE (4.3). Taking contributions from both the homogeneous and particular solutions of (4.3) and imposing (4.6) gives the expression
This theory will be termed ‘inertial CIDR’ or iCIDR, since, as will be shown, it captures the Bagnold scaling. In addition to satisfying (4.3) and (4.6), it is readily verified that the iCIDR constitutive functions (4.7)–(4.8) satisfy the inequalities (4.4)–(4.5). As such, the dynamic equations which result from iCIDR are guaranteed to be linearly well-posed for all deformations and for all values of the solids volume fraction.

Figure 5. Black lines plot the ratio
![]() $Y/p$
as a function of
$Y/p$
as a function of
![]() $I$
for varying values of the solids volume fraction
$I$
for varying values of the solids volume fraction
![]() $\unicode[STIX]{x1D719}$
in iCIDR. The blue line shows
$\unicode[STIX]{x1D719}$
in iCIDR. The blue line shows
![]() $Y/p=\unicode[STIX]{x1D707}(I)$
and the black dots show the steady isochoric state of each of the
$Y/p=\unicode[STIX]{x1D707}(I)$
and the black dots show the steady isochoric state of each of the
![]() $Y/p$
lines, i.e.
$Y/p$
lines, i.e.
![]() $I=\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D719})$
and
$I=\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D719})$
and
![]() $Y/p=\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D719}))$
. The dashed red line shows the value of
$Y/p=\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D719}))$
. The dashed red line shows the value of
![]() $\unicode[STIX]{x1D707}_{d}$
.
$\unicode[STIX]{x1D707}_{d}$
.
In
![]() $\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology
$\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology
![]() $I$
is tied rigidly to
$I$
is tied rigidly to
![]() $\unicode[STIX]{x1D719}$
through the
$\unicode[STIX]{x1D719}$
through the
![]() $I=\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D719})$
relation (2.12), whereas for iCIDR
$I=\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D719})$
relation (2.12), whereas for iCIDR
![]() $I$
evolves through the flow rule (4.2) given the dilatancy function (4.8). Substituting (4.8) into (4.2) yields the quadratic equation
$I$
evolves through the flow rule (4.2) given the dilatancy function (4.8). Substituting (4.8) into (4.2) yields the quadratic equation
which has the positive root
The right-hand side of (4.10) is a function of the solids volume fraction
![]() $\unicode[STIX]{x1D719}$
and the ratio
$\unicode[STIX]{x1D719}$
and the ratio
![]() $\text{div}\,\boldsymbol{u}/\Vert \unicode[STIX]{x1D64E}\Vert$
. Equation (2.9) can be used to determine an equation of state for the pressure
$\text{div}\,\boldsymbol{u}/\Vert \unicode[STIX]{x1D64E}\Vert$
. Equation (2.9) can be used to determine an equation of state for the pressure
This equation differs from (2.14) only in that
![]() $\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D719})$
is replaced by
$\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D719})$
is replaced by
![]() $I$
defined by (4.10). Since (4.10) depends on the velocity gradient only through the ratio
$I$
defined by (4.10). Since (4.10) depends on the velocity gradient only through the ratio
![]() $\text{div}\,\boldsymbol{u}/\Vert \unicode[STIX]{x1D64E}\Vert$
, which is unchanged by scaling the velocity gradient, (4.11) satisfies Bagnold scaling (Bagnold Reference Bagnold1954).
$\text{div}\,\boldsymbol{u}/\Vert \unicode[STIX]{x1D64E}\Vert$
, which is unchanged by scaling the velocity gradient, (4.11) satisfies Bagnold scaling (Bagnold Reference Bagnold1954).
According to (4.9), if
![]() $\Vert \unicode[STIX]{x1D64E}\Vert \rightarrow 0$
, then
$\Vert \unicode[STIX]{x1D64E}\Vert \rightarrow 0$
, then
![]() $I$
tends to either zero or infinity, depending on the sign of
$I$
tends to either zero or infinity, depending on the sign of
![]() $\text{div}\,\boldsymbol{u}$
. Hence, it seems that the iCIDR constitutive laws may break down if
$\text{div}\,\boldsymbol{u}$
. Hence, it seems that the iCIDR constitutive laws may break down if
![]() $\Vert \unicode[STIX]{x1D64E}\Vert =0$
. However, the inertial number
$\Vert \unicode[STIX]{x1D64E}\Vert =0$
. However, the inertial number
![]() $I$
can be bypassed by calculating an alternative expression for the pressure. Substituting (2.9) into (4.9) and solving for
$I$
can be bypassed by calculating an alternative expression for the pressure. Substituting (2.9) into (4.9) and solving for
![]() $p$
gives
$p$
gives
which is well defined for all deformation rates. Note that
![]() $p$
is strictly positive unless
$p$
is strictly positive unless
in which case the pressure is zero. Thus, in the absence of shear, there is no pressure if the grains are diverging from one another, but there is a finite, positive pressure if they are converging. Moreover, using the alignment condition (2.6), the yield function (4.7) and the definition of
![]() $I$
, it follows that the deviatoric stress is given by
$I$
, it follows that the deviatoric stress is given by
which is also well defined for all deformation rates. Finally, note that if
![]() $\unicode[STIX]{x1D719}\rightarrow \unicode[STIX]{x1D719}_{c}$
, then
$\unicode[STIX]{x1D719}\rightarrow \unicode[STIX]{x1D719}_{c}$
, then
![]() $\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D719})\rightarrow 0$
and the pressure tends to infinity (provided there is some straining).
$\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D719})\rightarrow 0$
and the pressure tends to infinity (provided there is some straining).
5 One-dimensional flow in a shear cell with the iCIDR rheology
The response of the iCIDR rheology is now tested in the one-dimensional gravitationless shear cell, as studied in § 3.2 for the
![]() $\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology. In this geometry the equation of state (4.12) implies the relations for the pressure
$\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology. In this geometry the equation of state (4.12) implies the relations for the pressure
and the deviatoric stresses (4.14)
Substituting these expressions into the conservation laws (3.1)–(3.3) and using the scalings (3.12) implies the non-dimensional iCIDR equations are
where the pressure is given by
The pressure (5.6) can be substituted directly into (5.4)–(5.5) to produce a system of three equations for
![]() $\unicode[STIX]{x1D719}$
,
$\unicode[STIX]{x1D719}$
,
![]() $\hat{u}$
and
$\hat{u}$
and
![]() ${\hat{w}}$
. Unlike the incompressible
${\hat{w}}$
. Unlike the incompressible
![]() $\unicode[STIX]{x1D707}(I)$
-rheology and the incompressible Navier–Stokes equations, in which pressure must be determined globally as part of solving the equations, all terms in this system (5.4)–(5.5) are explicitly specified locally. This makes the development of numerical methods much simpler.
$\unicode[STIX]{x1D707}(I)$
-rheology and the incompressible Navier–Stokes equations, in which pressure must be determined globally as part of solving the equations, all terms in this system (5.4)–(5.5) are explicitly specified locally. This makes the development of numerical methods much simpler.

Figure 6. (a) Numerical computations for the evolution of the one-dimensional vertical velocity
![]() ${\hat{w}}(\hat{z},\hat{t})$
for iCIDR. The initial conditions are given by (3.16) with
${\hat{w}}(\hat{z},\hat{t})$
for iCIDR. The initial conditions are given by (3.16) with
![]() $\unicode[STIX]{x1D719}_{0}=0.78$
,
$\unicode[STIX]{x1D719}_{0}=0.78$
,
![]() $\unicode[STIX]{x1D716}=0.05$
and
$\unicode[STIX]{x1D716}=0.05$
and
![]() ${\hat{H}}=30$
. The method of lines and first-order finite difference approximations are used to compute the solution, which is shown at a sequence of times with
${\hat{H}}=30$
. The method of lines and first-order finite difference approximations are used to compute the solution, which is shown at a sequence of times with
![]() $N_{z}=47$
grid points (open circles) and
$N_{z}=47$
grid points (open circles) and
![]() $N_{z}=201$
grid points (solid lines). This explicitly demonstrates that the numerical solution is grid converged. (b) The evolution of the maximum vertical velocity in time for
$N_{z}=201$
grid points (solid lines). This explicitly demonstrates that the numerical solution is grid converged. (b) The evolution of the maximum vertical velocity in time for
![]() $N_{z}=47$
grid points (blue circles) and
$N_{z}=47$
grid points (blue circles) and
![]() $N_{z}=201$
grid points (red solid line). The numerical solution is very close to the steady-state solution (3.10) by 10 non-dimensional units. Supplementary movies 4 and 5 show the evolution of
$N_{z}=201$
grid points (red solid line). The numerical solution is very close to the steady-state solution (3.10) by 10 non-dimensional units. Supplementary movies 4 and 5 show the evolution of
![]() $\unicode[STIX]{x1D719}(\hat{z},\hat{t})$
,
$\unicode[STIX]{x1D719}(\hat{z},\hat{t})$
,
![]() $\hat{u} (\hat{z},\hat{t})$
and
$\hat{u} (\hat{z},\hat{t})$
and
![]() ${\hat{w}}(\hat{z},\hat{t})$
for both the finite difference and Chebyshev spectral discretizations.
${\hat{w}}(\hat{z},\hat{t})$
for both the finite difference and Chebyshev spectral discretizations.

Figure 7. Time-dependent numerical simulation for iCIDR. The flow starts from the perturbed initial conditions (5.7) with
![]() $\unicode[STIX]{x1D719}_{0}=0.78$
,
$\unicode[STIX]{x1D719}_{0}=0.78$
,
![]() $\hat{a}=0.16$
and
$\hat{a}=0.16$
and
![]() $\hat{b}=0.1$
and converges towards the steady solution (3.10). In panels (a–c) the solid lines correspond to a high spatial resolution (
$\hat{b}=0.1$
and converges towards the steady solution (3.10). In panels (a–c) the solid lines correspond to a high spatial resolution (
![]() $N_{z}=201$
) and open circles to a lower resolution (
$N_{z}=201$
) and open circles to a lower resolution (
![]() $N_{z}=47$
). Panel (d) is a plot of
$N_{z}=47$
). Panel (d) is a plot of
![]() $\unicode[STIX]{x1D712}$
defined in (A 18) at
$\unicode[STIX]{x1D712}$
defined in (A 18) at
![]() $t=0$
, which implies that, unlike iCIDR, the
$t=0$
, which implies that, unlike iCIDR, the
![]() $\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology would be strongly ill-posed for these initial conditions. (e) The iCIDR constitutive relations ensure that at both low (open circles,
$\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology would be strongly ill-posed for these initial conditions. (e) The iCIDR constitutive relations ensure that at both low (open circles,
![]() $N_{z}=47$
) and high (solid red line,
$N_{z}=47$
) and high (solid red line,
![]() $N_{z}=201$
) spatial resolution the maximum vertical velocity
$N_{z}=201$
) spatial resolution the maximum vertical velocity
![]() ${\hat{w}}$
decays to the steady-state value
${\hat{w}}$
decays to the steady-state value
![]() ${\hat{w}}=0$
everywhere. An animation of the simulation (supplementary movie 6) is available in the online supplementary material.
${\hat{w}}=0$
everywhere. An animation of the simulation (supplementary movie 6) is available in the online supplementary material.
Figure 6(a) and supplementary movies 4 and 5 show numerical solutions according to iCIDR for the one-dimensional gravity-free flow of § 3, specifically for initial conditions (3.16). Note that the solution converges smoothly to steady state, the same steady state as for the
![]() $\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology (3.10), without any sign of the catastrophic resolution-dependent blow-up seen before. The simulations are computed using the method of lines with the finite difference discretization for both
$\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology (3.10), without any sign of the catastrophic resolution-dependent blow-up seen before. The simulations are computed using the method of lines with the finite difference discretization for both
![]() $N_{z}=47$
and 201 grid points. Note that the solutions in figure 6(a) lie directly on top of one another! This shows that these solutions are grid converged.
$N_{z}=47$
and 201 grid points. Note that the solutions in figure 6(a) lie directly on top of one another! This shows that these solutions are grid converged.
The fact that the iCIDR equations are mathematically well-posed suggests that they can handle larger perturbations from steady state than (3.16). An interesting test case is an initial condition with
![]() $|\unicode[STIX]{x2202}_{\hat{z}}\hat{u} |=0$
for at least one point. This is interesting because the function
$|\unicode[STIX]{x2202}_{\hat{z}}\hat{u} |=0$
for at least one point. This is interesting because the function
![]() $\unicode[STIX]{x1D712}$
, defined in (A 18), is infinite when
$\unicode[STIX]{x1D712}$
, defined in (A 18), is infinite when
![]() $|\unicode[STIX]{x2202}_{\hat{z}}\hat{u} |=0$
, so the
$|\unicode[STIX]{x2202}_{\hat{z}}\hat{u} |=0$
, so the
![]() $\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology is strongly unstable even at low resolution. Following this idea, the results of a simulation with the initial condition
$\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology is strongly unstable even at low resolution. Following this idea, the results of a simulation with the initial condition
are plotted in figure 7. As figure 7(d) shows, with the parameters
![]() $\unicode[STIX]{x1D719}_{0}=0.78$
,
$\unicode[STIX]{x1D719}_{0}=0.78$
,
![]() $\hat{a}=0.16$
and
$\hat{a}=0.16$
and
![]() $\hat{b}=0.1$
, there is a large central region where
$\hat{b}=0.1$
, there is a large central region where
![]() $\unicode[STIX]{x1D712}>0$
and two points where
$\unicode[STIX]{x1D712}>0$
and two points where
![]() $\unicode[STIX]{x1D712}$
is infinite. This problem is therefore very strongly ill-posed for the
$\unicode[STIX]{x1D712}$
is infinite. This problem is therefore very strongly ill-posed for the
![]() $\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology. Ill-posed behaviour has been verified numerically; indeed, for these initial conditions, even for the coarse grid with
$\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology. Ill-posed behaviour has been verified numerically; indeed, for these initial conditions, even for the coarse grid with
![]() $N_{z}=47$
, the solution blows up (not shown). By contrast, with the iCIDR equations (5.3)–(5.6) there is no catastrophic blow-up and the simulations smoothly evolve from the initial conditions towards the steady-state solution (3.10) as shown in supplementary movie 6 and in figure 7(a–c) for both high- and low-resolution runs. This convergence is also exhibited in figure 7(e) where the maximum vertical velocity is plotted as a function of time: note that the graphs for different resolutions lie on top of one another.
$N_{z}=47$
, the solution blows up (not shown). By contrast, with the iCIDR equations (5.3)–(5.6) there is no catastrophic blow-up and the simulations smoothly evolve from the initial conditions towards the steady-state solution (3.10) as shown in supplementary movie 6 and in figure 7(a–c) for both high- and low-resolution runs. This convergence is also exhibited in figure 7(e) where the maximum vertical velocity is plotted as a function of time: note that the graphs for different resolutions lie on top of one another.
It is interesting to examine the structure of the solution in figure 7. Initially there is a rapid readjustment of the two velocity components with a time constant of the order of one time unit. The solids volume fraction starts out independent of
![]() $\hat{z}$
, but it develops a non-trivial profile which changes sign and then decays much more slowly. The latter evolution is responsible for the local maximum of
$\hat{z}$
, but it develops a non-trivial profile which changes sign and then decays much more slowly. The latter evolution is responsible for the local maximum of
![]() $|{\hat{w}}|$
near
$|{\hat{w}}|$
near
![]() $\hat{t}=3$
shown in figure 7(e).
$\hat{t}=3$
shown in figure 7(e).
6 Comparison of iCIDR with DEM simulations
The DEM calculations detailed in appendix C and figure 1, which were used to recover the steady
![]() $\unicode[STIX]{x1D707}(I)$
and
$\unicode[STIX]{x1D707}(I)$
and
![]() $\unicode[STIX]{x1D6F7}(I)$
relations, are also capable of verifying the time-dependent characteristics of the iCIDR solutions. Here new DEM simulations are initialized with the same procedure that was used to obtain the steady linear shearing solution (3.10), but then the velocity fields are replaced with the sinusoidally perturbed profiles (5.7) discussed in the previous section. As expected, this results in a decay from these applied fields back towards the steady solution. Figure 8 shows that the iCIDR solutions differ by less than 2.5 % relative error from the DEM simulations throughout the dynamics. Figure 8(a–c) shows that iCIDR captures the spatial variation of the three flow variables
$\unicode[STIX]{x1D6F7}(I)$
relations, are also capable of verifying the time-dependent characteristics of the iCIDR solutions. Here new DEM simulations are initialized with the same procedure that was used to obtain the steady linear shearing solution (3.10), but then the velocity fields are replaced with the sinusoidally perturbed profiles (5.7) discussed in the previous section. As expected, this results in a decay from these applied fields back towards the steady solution. Figure 8 shows that the iCIDR solutions differ by less than 2.5 % relative error from the DEM simulations throughout the dynamics. Figure 8(a–c) shows that iCIDR captures the spatial variation of the three flow variables
![]() $\unicode[STIX]{x1D719}$
,
$\unicode[STIX]{x1D719}$
,
![]() $\hat{u}$
and
$\hat{u}$
and
![]() ${\hat{w}}$
. Figure 8(d) indicates that it also captures complex details of the time evolution. Although more testing is needed, this agreement indicates that iCIDR correctly represents significant aspects of the rheology.
${\hat{w}}$
. Figure 8(d) indicates that it also captures complex details of the time evolution. Although more testing is needed, this agreement indicates that iCIDR correctly represents significant aspects of the rheology.

Figure 8. A comparison between the iCIDR continuum calculation, detailed in figure 7, and the results of two-dimensional DEM simulations initialized with the same flow fields. Circles are the mean values and error bars represent the standard deviation of 10 repeat DEM simulations. Supplementary movies 7 and 8 show the evolution of the coarse-grained velocity components
![]() $\hat{u}$
and
$\hat{u}$
and
![]() ${\hat{w}}$
alongside renderings of the particles during the simulation. Note that
${\hat{w}}$
alongside renderings of the particles during the simulation. Note that
![]() $\hat{u}$
obtained by DEM simulations is given by the relative velocity between the bottom (
$\hat{u}$
obtained by DEM simulations is given by the relative velocity between the bottom (
![]() $\hat{z}=0$
) and top (
$\hat{z}=0$
) and top (
![]() $\hat{z}={\hat{H}}$
) layers under the Lees–Edwards boundary conditions in order to simplify the comparison with the iCIDR continuum calculation.
$\hat{z}={\hat{H}}$
) layers under the Lees–Edwards boundary conditions in order to simplify the comparison with the iCIDR continuum calculation.
7 Discussion of related issues
7.1 Remarks on ill-posedness
Issues of ill-posedness in
![]() $\unicode[STIX]{x1D707}(I)$
-rheology were first raised in Barker et al. (Reference Barker, Schaeffer, Bohorquez and Gray2015). It was shown that, although the dynamic equations derived from incompressible
$\unicode[STIX]{x1D707}(I)$
-rheology were first raised in Barker et al. (Reference Barker, Schaeffer, Bohorquez and Gray2015). It was shown that, although the dynamic equations derived from incompressible
![]() $\unicode[STIX]{x1D707}(I)$
-rheology are mathematically well-posed for a large range of inertial numbers, the system is ill-posed when
$\unicode[STIX]{x1D707}(I)$
-rheology are mathematically well-posed for a large range of inertial numbers, the system is ill-posed when
![]() $I$
is too high or too low. The following remarks may help reconcile this ill-posedness with the fact that problems of practical interest (e.g. Lagrée et al.
Reference Lagrée, Staron and Popinet2011; Staron et al.
Reference Staron, Lagrée and Popinet2012) have apparently been successfully solved numerically using
$I$
is too high or too low. The following remarks may help reconcile this ill-posedness with the fact that problems of practical interest (e.g. Lagrée et al.
Reference Lagrée, Staron and Popinet2011; Staron et al.
Reference Staron, Lagrée and Popinet2012) have apparently been successfully solved numerically using
![]() $\unicode[STIX]{x1D707}(I)$
-rheology.
$\unicode[STIX]{x1D707}(I)$
-rheology.
In the first place, ill-posedness effects may be masked in simulations performed on a low-resolution grid, as in § 4 of this paper. Specifically, numerical diffusion may be sufficient to suppress the instability. Ill-posedness may become apparent only through careful comparison of progressively mesh-refined simulations – see figure 4 of Barker & Gray (Reference Barker and Gray2017) and figure 21 of Martin et al. (Reference Martin, Ionescu, Mangeney, Bouchut and Farin2017); in these papers certain spurious flow features continue to become ever more finely scaled as the grid size gets smaller. It is sometimes suggested that low-resolution solutions of an ill-posed model might be sufficient for some practical purposes. However, such approaches are scientifically flawed, because the results rely on numerical diffusion to regularize the problem, which is dependent on both grid size and numerical scheme, and is often not known precisely. In our view it is far better to try to understand what physics is missing in the model, and only compute solutions when a well-posed theory has been formulated.
Other issues are the following. (i) In some problems, such as column collapse (Lagrée et al. Reference Lagrée, Staron and Popinet2011), the ill-posed region of parameter space may only be active for a short period of time. In such cases careful comparison of numerical results at different spatial resolutions, including some very fine grids, may be needed for non-convergence to become apparent (Barker et al. Reference Barker, Schaeffer, Bohorquez and Gray2015; Barker & Gray Reference Barker and Gray2017; Martin et al. Reference Martin, Ionescu, Mangeney, Bouchut and Farin2017). (ii) Ill-posedness may also be partially suppressed by attempts to remove the singularity in the viscosity at low strain rates. Many numerical codes do this by introducing an upper bound on the viscosity, which implies that the material reverts to a Newtonian fluid for slow flows. However, these procedures are ad hoc in nature, and there is no guarantee that ill-posedness is suppressed completely.
In this subsection attention has been focused on the consequences of ill-posedness that may be seen through computations. However, on the mathematical side, it seems likely that solutions of an ill-posed initial-value problem exist only for a very restricted set of initial conditions, far too restricted to model physical problems. A rigorous proof of this assertion for complicated PDEs like iCIDR would be difficult, but for a simpler example let us refer to appendix 2 of Barker et al. (Reference Barker, Schaeffer, Shearer and Gray2017) for a proof of the following fact: the backwards heat equation
where
![]() $\unicode[STIX]{x1D716}\neq 0$
, cannot be solved on any non-zero interval
$\unicode[STIX]{x1D716}\neq 0$
, cannot be solved on any non-zero interval
![]() $\{0<t<t_{0}\}$
unless
$\{0<t<t_{0}\}$
unless
![]() $p$
is an even non-negative integer. The singularities of the initial conditions at
$p$
is an even non-negative integer. The singularities of the initial conditions at
![]() $x=n\unicode[STIX]{x03C0}$
,
$x=n\unicode[STIX]{x03C0}$
,
![]() $n=0,\pm 1,\pm 2,\ldots$
(which are extremely mild if
$n=0,\pm 1,\pm 2,\ldots$
(which are extremely mild if
![]() $p$
is large) make such solutions impossible.
$p$
is large) make such solutions impossible.
7.2 Behaviour at the boundary of and outside the inertial regime
Regarding the boundary of the inertial regime, note in (2.14) and (5.11) that
![]() $p$
tends to infinity as
$p$
tends to infinity as
![]() $\unicode[STIX]{x1D719}\rightarrow \unicode[STIX]{x1D719}_{c}$
. In DEM simulations, Chialvo et al. (Reference Chialvo, Sun and Sundaresan2012) found that this growth was cut off and blended into the pressure from the intermediate regime through the formula
$\unicode[STIX]{x1D719}\rightarrow \unicode[STIX]{x1D719}_{c}$
. In DEM simulations, Chialvo et al. (Reference Chialvo, Sun and Sundaresan2012) found that this growth was cut off and blended into the pressure from the intermediate regime through the formula
where
Thus the pressure tends to
![]() $p_{itm}$
as
$p_{itm}$
as
![]() $\unicode[STIX]{x1D719}\rightarrow \unicode[STIX]{x1D719}_{c}$
, where the limit pressure depends on the elastic modulus. Although it is beyond the scope of the present paper, it is anticipated that a more complete version of CIDR would remain valid across regime boundaries.
$\unicode[STIX]{x1D719}\rightarrow \unicode[STIX]{x1D719}_{c}$
, where the limit pressure depends on the elastic modulus. Although it is beyond the scope of the present paper, it is anticipated that a more complete version of CIDR would remain valid across regime boundaries.
Granular flow at densities
![]() $\unicode[STIX]{x1D719}>\unicode[STIX]{x1D719}_{c}$
(provided the strain rate is not too large) corresponds to what is called the quasi-static regime (Otsuki & Hayakawa Reference Otsuki and Hayakawa2009; Chialvo et al.
Reference Chialvo, Sun and Sundaresan2012; Singh et al.
Reference Singh, Magnanimo, Saitoh and Luding2015). In this regime stresses may remain non-zero even as the strain rate tends to zero, i.e. a static yield stress exists; the scale of these static stresses is set by
$\unicode[STIX]{x1D719}>\unicode[STIX]{x1D719}_{c}$
(provided the strain rate is not too large) corresponds to what is called the quasi-static regime (Otsuki & Hayakawa Reference Otsuki and Hayakawa2009; Chialvo et al.
Reference Chialvo, Sun and Sundaresan2012; Singh et al.
Reference Singh, Magnanimo, Saitoh and Luding2015). In this regime stresses may remain non-zero even as the strain rate tends to zero, i.e. a static yield stress exists; the scale of these static stresses is set by
![]() $k/d$
, where
$k/d$
, where
![]() $k$
is the spring constant in DEM simulations.
$k$
is the spring constant in DEM simulations.
CIDR is a general theory that can model granular material outside, as well as inside, of the inertial regime. In particular, the version of CIDR in § 2(e) of Barker et al. (Reference Barker, Schaeffer, Shearer and Gray2017), which was motivated by critical state soil mechanics (Schofield & Wroth Reference Schofield and Wroth1968), has a non-zero static yield stress, as in the quasi-static regime in DEM simulations. (In that paper, to facilitate comparison with Silbert et al. (Reference Silbert, Ertaş, Grest, Halsey, Levine and Plimpton2001), the stress scale was chosen as
![]() $\unicode[STIX]{x1D70C}_{\ast }gd$
, i.e. dependent on gravitational acceleration
$\unicode[STIX]{x1D70C}_{\ast }gd$
, i.e. dependent on gravitational acceleration
![]() $g$
. This was an unfortunate choice with no intrinsic significance. A more appropriate choice would have been
$g$
. This was an unfortunate choice with no intrinsic significance. A more appropriate choice would have been
![]() $k/d$
, where
$k/d$
, where
![]() $k$
is the spring constant in DEM simulations.)
$k$
is the spring constant in DEM simulations.)
7.3 Extensions to the theory
Inertial CIDR is also able to incorporate non-monotonicity of the
![]() $\unicode[STIX]{x1D707}(I)$
function (DeGiuli & Wyart Reference DeGiuli and Wyart2017), which is crucial for modelling hysteretic effects, such as coexisting static and moving regions, in depth-averaged avalanche models (Daerr & Douady Reference Daerr and Douady1999; Pouliquen & Forterre Reference Pouliquen and Forterre2002; Edwards & Gray Reference Edwards and Gray2015; Edwards et al.
Reference Edwards, Viroulet, Kokelaar and Gray2017; Russell et al.
Reference Russell, Johnson, Edwards, Viroulet, Rocha and Gray2019). Non-monotonic
$\unicode[STIX]{x1D707}(I)$
function (DeGiuli & Wyart Reference DeGiuli and Wyart2017), which is crucial for modelling hysteretic effects, such as coexisting static and moving regions, in depth-averaged avalanche models (Daerr & Douady Reference Daerr and Douady1999; Pouliquen & Forterre Reference Pouliquen and Forterre2002; Edwards & Gray Reference Edwards and Gray2015; Edwards et al.
Reference Edwards, Viroulet, Kokelaar and Gray2017; Russell et al.
Reference Russell, Johnson, Edwards, Viroulet, Rocha and Gray2019). Non-monotonic
![]() $\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}(I)$
functions are problematic in the incompressible
$\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}(I)$
functions are problematic in the incompressible
![]() $\unicode[STIX]{x1D707}(I)$
-rheology, because they imply that the theory is always ill-posed in regions of decreasing friction (Barker et al.
Reference Barker, Schaeffer, Bohorquez and Gray2015). For iCIDR, however, having a non-monotonic
$\unicode[STIX]{x1D707}(I)$
-rheology, because they imply that the theory is always ill-posed in regions of decreasing friction (Barker et al.
Reference Barker, Schaeffer, Bohorquez and Gray2015). For iCIDR, however, having a non-monotonic
![]() $\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}(I)$
function is not a problem, because it is formulated in terms of the solids volume fraction, i.e.
$\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}(I)$
function is not a problem, because it is formulated in terms of the solids volume fraction, i.e.
![]() $\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D719}))$
, and so it does not affect the well-posedness conditions (4.3)–(4.5).
$\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D719}))$
, and so it does not affect the well-posedness conditions (4.3)–(4.5).
At present iCIDR is explicitly a local theory which cannot account for the observed role of fluctuations that inspired the non-local theories of Pouliquen & Forterre (Reference Pouliquen and Forterre2009), Kamrin & Koval (Reference Kamrin and Koval2012) and Bouzid et al. (Reference Bouzid, Trulsson, Claudin, Clément and Andreotti2013). Inclusion of these effects is an important direction for future work.
8 Conclusions
The iCIDR equations, introduced in this paper, provide a continuum model for fluid-like inertial flows of rigid spherical particles that lie below a critical volume fraction, above which the compressibility of the grains becomes important (Otsuki & Hayakawa Reference Otsuki and Hayakawa2009; Chialvo et al.
Reference Chialvo, Sun and Sundaresan2012). One striking aspect of the iCIDR theory is its simplicity: it is a minimal extension of
![]() $\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology with no extra variables, no extra parameters, no extra evolution equations beyond conservation of mass and momentum and no extra boundary conditions. While retaining the success of
$\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology with no extra variables, no extra parameters, no extra evolution equations beyond conservation of mass and momentum and no extra boundary conditions. While retaining the success of
![]() $\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology for steady inertial flow, iCIDR is well-posed, thermodynamically sound (Onsager symmetric and dissipative) and agrees well with transient DEM simulations in a one-dimensional gravity-free shear cell.
$\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology for steady inertial flow, iCIDR is well-posed, thermodynamically sound (Onsager symmetric and dissipative) and agrees well with transient DEM simulations in a one-dimensional gravity-free shear cell.
Inertial CIDR is very well suited to numerical calculations because the pressure is defined by a local equation of state. This contrasts with incompressible theories, in which the pressure can only be found globally as part of solving the equations. The numerical simulations presented in this paper are therefore a particularly encouraging proof of concept and it is hoped that other existing numerical methods can similarly be modified in order to bring the advantages of the iCIDR formulation to a wide range of practical applications.
Acknowledgements
The research of M.S. is supported by National Science Foundation grant DMS-1812445. This research was also supported by NERC grants NE/E003206/1 and NE/K003011/1 as well as EPSRC grants EP/I019189/1, EP/K00428X/1 and EP/M022447/1. J.M.N.T.G. is a Royal Society Wolfson Research Merit Award holder (WM150058) and an EPSRC Established Career Fellow (EP/M022447/1). All research data supporting this publication are directly available within the article.
Supplementary movies
Supplementary movies are available at https://doi.org/10.1017/jfm.2019.476.
Appendix A. Ill-posedness of the one-dimensional
 $\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology
$\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology
Although there are some technical complications, effectively the dynamic equations of
![]() $\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology for two-dimensional flow are always ill-posed (Heyman et al.
Reference Heyman, Delannay, Tabuteau and Valance2017). As in Barker et al. (Reference Barker, Schaeffer, Bohorquez and Gray2015), the ill-posedness has a directional character: plane-wave solutions (in all space) in certain directions suffer uncontrolled growth while those in other directions decay smoothly to uniform flow. If, as in § 3, solutions depending on only one spatial variable are sought, these one-dimensional equations may be either well-posed or ill-posed, depending on whether the one independent direction retained corresponds to one of the stable or unstable directions. In this appendix, conditions for the ill-posedness of the one-dimensional system (3.1)–(3.8) are derived.
$\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology for two-dimensional flow are always ill-posed (Heyman et al.
Reference Heyman, Delannay, Tabuteau and Valance2017). As in Barker et al. (Reference Barker, Schaeffer, Bohorquez and Gray2015), the ill-posedness has a directional character: plane-wave solutions (in all space) in certain directions suffer uncontrolled growth while those in other directions decay smoothly to uniform flow. If, as in § 3, solutions depending on only one spatial variable are sought, these one-dimensional equations may be either well-posed or ill-posed, depending on whether the one independent direction retained corresponds to one of the stable or unstable directions. In this appendix, conditions for the ill-posedness of the one-dimensional system (3.1)–(3.8) are derived.
The equations (3.1)–(3.3) together with (3.6) and (3.8) are linearized around a base flow
![]() $(\unicode[STIX]{x1D719}^{0},u^{0},w^{0})$
in the dependent variables
$(\unicode[STIX]{x1D719}^{0},u^{0},w^{0})$
in the dependent variables
![]() $(\unicode[STIX]{x1D719},u,w)$
by introducing perturbations
$(\unicode[STIX]{x1D719},u,w)$
by introducing perturbations
![]() $(\breve{\unicode[STIX]{x1D719}},\breve{u},\breve{w})$
of the form
$(\breve{\unicode[STIX]{x1D719}},\breve{u},\breve{w})$
of the form
 $$\begin{eqnarray}\left[\begin{array}{@{}c@{}}\unicode[STIX]{x1D719}\\ u\\ w\end{array}\right]=\left[\begin{array}{@{}c@{}}\unicode[STIX]{x1D719}^{0}(z,t)\\ u^{0}(z,t)\\ w^{0}(z,t)\end{array}\right]+\left[\begin{array}{@{}c@{}}\breve{\unicode[STIX]{x1D719}}(z,t)\\ \breve{u}(z,t)\\ \breve{w}(z,t)\end{array}\right],\end{eqnarray}$$
$$\begin{eqnarray}\left[\begin{array}{@{}c@{}}\unicode[STIX]{x1D719}\\ u\\ w\end{array}\right]=\left[\begin{array}{@{}c@{}}\unicode[STIX]{x1D719}^{0}(z,t)\\ u^{0}(z,t)\\ w^{0}(z,t)\end{array}\right]+\left[\begin{array}{@{}c@{}}\breve{\unicode[STIX]{x1D719}}(z,t)\\ \breve{u}(z,t)\\ \breve{w}(z,t)\end{array}\right],\end{eqnarray}$$
and then freezing the base flow coefficients. In the linearization the highest-order derivatives of the perturbed variables are retained in each equation, together with the convective derivatives. This leads to linearized equations of the form
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{t}\left[\begin{array}{@{}c@{}}\breve{\unicode[STIX]{x1D719}}\\ \breve{u}\\ \breve{w}\end{array}\right]=\left[\begin{array}{@{}ccc@{}}-w^{0}\unicode[STIX]{x2202}_{z} & 0 & -\unicode[STIX]{x1D719}^{0}\unicode[STIX]{x2202}_{z}\\ a_{1}\unicode[STIX]{x2202}_{z} & b_{11}\unicode[STIX]{x2202}_{zz}-w^{0}\unicode[STIX]{x2202}_{z} & b_{12}\unicode[STIX]{x2202}_{zz}\\ a_{2}\unicode[STIX]{x2202}_{z} & b_{21}\unicode[STIX]{x2202}_{zz} & b_{22}\unicode[STIX]{x2202}_{zz}-w^{0}\unicode[STIX]{x2202}_{z}\end{array}\right]\left[\begin{array}{@{}c@{}}\breve{\unicode[STIX]{x1D719}}\\ \breve{u}\\ \breve{w}\end{array}\right],\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}\left[\begin{array}{@{}c@{}}\breve{\unicode[STIX]{x1D719}}\\ \breve{u}\\ \breve{w}\end{array}\right]=\left[\begin{array}{@{}ccc@{}}-w^{0}\unicode[STIX]{x2202}_{z} & 0 & -\unicode[STIX]{x1D719}^{0}\unicode[STIX]{x2202}_{z}\\ a_{1}\unicode[STIX]{x2202}_{z} & b_{11}\unicode[STIX]{x2202}_{zz}-w^{0}\unicode[STIX]{x2202}_{z} & b_{12}\unicode[STIX]{x2202}_{zz}\\ a_{2}\unicode[STIX]{x2202}_{z} & b_{21}\unicode[STIX]{x2202}_{zz} & b_{22}\unicode[STIX]{x2202}_{zz}-w^{0}\unicode[STIX]{x2202}_{z}\end{array}\right]\left[\begin{array}{@{}c@{}}\breve{\unicode[STIX]{x1D719}}\\ \breve{u}\\ \breve{w}\end{array}\right],\end{eqnarray}$$
where
![]() $a_{i}$
and
$a_{i}$
and
![]() $b_{ij}$
are constant coefficients derived from the pressure (3.6) and the deviatoric stresses (3.8).
$b_{ij}$
are constant coefficients derived from the pressure (3.6) and the deviatoric stresses (3.8).
The linearized system (A 2) admits normal-mode solutions of the form
 $$\begin{eqnarray}\left[\begin{array}{@{}c@{}}\breve{\unicode[STIX]{x1D719}}(z,t)\\ \breve{u}(z,t)\\ \breve{w}(z,t)\end{array}\right]=\text{e}^{\text{i}\unicode[STIX]{x1D709}z+\unicode[STIX]{x1D706}t}\left[\begin{array}{@{}c@{}}\tilde{\unicode[STIX]{x1D719}}\\ \tilde{u} \\ \tilde{w}\end{array}\right],\end{eqnarray}$$
$$\begin{eqnarray}\left[\begin{array}{@{}c@{}}\breve{\unicode[STIX]{x1D719}}(z,t)\\ \breve{u}(z,t)\\ \breve{w}(z,t)\end{array}\right]=\text{e}^{\text{i}\unicode[STIX]{x1D709}z+\unicode[STIX]{x1D706}t}\left[\begin{array}{@{}c@{}}\tilde{\unicode[STIX]{x1D719}}\\ \tilde{u} \\ \tilde{w}\end{array}\right],\end{eqnarray}$$
in which
![]() $\unicode[STIX]{x1D709}$
is the wavenumber,
$\unicode[STIX]{x1D709}$
is the wavenumber,
![]() $\unicode[STIX]{x1D706}$
is the temporal growth rate and
$\unicode[STIX]{x1D706}$
is the temporal growth rate and
![]() $\tilde{\unicode[STIX]{x1D719}}$
,
$\tilde{\unicode[STIX]{x1D719}}$
,
![]() $\tilde{u}$
and
$\tilde{u}$
and
![]() $\tilde{w}$
are constants. Substituting these into (A 2) reveals that
$\tilde{w}$
are constants. Substituting these into (A 2) reveals that
![]() $\unicode[STIX]{x1D706}$
must be an eigenvalue of the matrix
$\unicode[STIX]{x1D706}$
must be an eigenvalue of the matrix
 $$\begin{eqnarray}\unicode[STIX]{x1D63C}(\unicode[STIX]{x1D709})=\left[\begin{array}{@{}ccc@{}}-\text{i}w^{0}\unicode[STIX]{x1D709} & 0 & -\text{i}\unicode[STIX]{x1D719}^{0}\unicode[STIX]{x1D709}\\ \text{i}a_{1}\unicode[STIX]{x1D709} & -b_{11}\unicode[STIX]{x1D709}^{2}-\text{i}w^{0}\unicode[STIX]{x1D709} & -b_{12}\unicode[STIX]{x1D709}^{2}\\ \text{i}a_{2}\unicode[STIX]{x1D709} & -b_{21}\unicode[STIX]{x1D709}^{2} & -b_{22}\unicode[STIX]{x1D709}^{2}-\text{i}w^{0}\unicode[STIX]{x1D709}\end{array}\right].\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D63C}(\unicode[STIX]{x1D709})=\left[\begin{array}{@{}ccc@{}}-\text{i}w^{0}\unicode[STIX]{x1D709} & 0 & -\text{i}\unicode[STIX]{x1D719}^{0}\unicode[STIX]{x1D709}\\ \text{i}a_{1}\unicode[STIX]{x1D709} & -b_{11}\unicode[STIX]{x1D709}^{2}-\text{i}w^{0}\unicode[STIX]{x1D709} & -b_{12}\unicode[STIX]{x1D709}^{2}\\ \text{i}a_{2}\unicode[STIX]{x1D709} & -b_{21}\unicode[STIX]{x1D709}^{2} & -b_{22}\unicode[STIX]{x1D709}^{2}-\text{i}w^{0}\unicode[STIX]{x1D709}\end{array}\right].\end{eqnarray}$$
The imaginary terms
![]() $-\text{i}w^{0}\unicode[STIX]{x1D709}$
on the diagonal shift the eigenvalues
$-\text{i}w^{0}\unicode[STIX]{x1D709}$
on the diagonal shift the eigenvalues
![]() $\unicode[STIX]{x1D706}$
, but do not affect stability or well-posedness, which are governed by the real part of
$\unicode[STIX]{x1D706}$
, but do not affect stability or well-posedness, which are governed by the real part of
![]() $\unicode[STIX]{x1D706}$
. The vertical component of the base state velocity
$\unicode[STIX]{x1D706}$
. The vertical component of the base state velocity
![]() $w^{0}$
is therefore set to zero in what follows.
$w^{0}$
is therefore set to zero in what follows.
Denoting the bottom right
![]() $2\times 2$
matrix of terms multiplying
$2\times 2$
matrix of terms multiplying
![]() $-\unicode[STIX]{x1D709}^{2}$
as
$-\unicode[STIX]{x1D709}^{2}$
as
the eigenvalues are calculated by solving
where the coefficients are
To test for ill-posedness, the large-wavenumber limit
![]() $\unicode[STIX]{x1D709}\rightarrow \infty$
is taken. Balancing the order of terms in (A 6), it is clear that
$\unicode[STIX]{x1D709}\rightarrow \infty$
is taken. Balancing the order of terms in (A 6), it is clear that
![]() $\unicode[STIX]{x1D706}(\unicode[STIX]{x1D709})\sim \unicode[STIX]{x1D709}^{2}$
, so the substitution
$\unicode[STIX]{x1D706}(\unicode[STIX]{x1D709})\sim \unicode[STIX]{x1D709}^{2}$
, so the substitution
![]() $\unicode[STIX]{x1D706}=\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D709}^{2}$
is made. Then the terms of maximal order in (A 6), i.e.
$\unicode[STIX]{x1D706}=\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D709}^{2}$
is made. Then the terms of maximal order in (A 6), i.e.
![]() $O(\unicode[STIX]{x1D709}^{6})$
, have the coefficient
$O(\unicode[STIX]{x1D709}^{6})$
, have the coefficient
![]() $\unicode[STIX]{x1D6EC}^{3}+(\text{tr}\,\unicode[STIX]{x1D71E})\unicode[STIX]{x1D6EC}^{2}+(\det \unicode[STIX]{x1D71E})\unicode[STIX]{x1D6EC}$
. Thus, to leading order, either
$\unicode[STIX]{x1D6EC}^{3}+(\text{tr}\,\unicode[STIX]{x1D71E})\unicode[STIX]{x1D6EC}^{2}+(\det \unicode[STIX]{x1D71E})\unicode[STIX]{x1D6EC}$
. Thus, to leading order, either
![]() $\unicode[STIX]{x1D6EC}=0$
, or
$\unicode[STIX]{x1D6EC}=0$
, or
![]() $\unicode[STIX]{x1D6EC}$
is a solution of
$\unicode[STIX]{x1D6EC}$
is a solution of
i.e. one of the two roots
To determine the signs of these roots, the coefficients in (A 2) are now evaluated. If the superscript 0 notation is dropped, the coefficients in (A 2) are then
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle a_{1}=\frac{2d^{2}}{\unicode[STIX]{x1D719}}\unicode[STIX]{x2202}_{z}u\Vert \unicode[STIX]{x1D64E}\Vert \unicode[STIX]{x2202}_{\unicode[STIX]{x1D719}}\left(\frac{M(\unicode[STIX]{x1D719})}{\unicode[STIX]{x1D6F9}^{2}(\unicode[STIX]{x1D719})}\right),\\ \displaystyle a_{2}=\frac{2d^{2}\Vert \unicode[STIX]{x1D64E}\Vert }{\unicode[STIX]{x1D719}}\left[\unicode[STIX]{x2202}_{z}w\unicode[STIX]{x2202}_{\unicode[STIX]{x1D719}}\left(\frac{M(\unicode[STIX]{x1D719})}{\unicode[STIX]{x1D6F9}^{2}(\unicode[STIX]{x1D719})}\right)-2\Vert \unicode[STIX]{x1D64E}\Vert \unicode[STIX]{x2202}_{\unicode[STIX]{x1D719}}\left(\frac{1}{\unicode[STIX]{x1D6F9}^{2}(\unicode[STIX]{x1D719})}\right)\right],\\ \displaystyle b_{11}=\frac{d^{2}M(\unicode[STIX]{x1D719})}{2\unicode[STIX]{x1D719}\unicode[STIX]{x1D6F9}^{2}(\unicode[STIX]{x1D719})}\frac{2(\unicode[STIX]{x2202}_{z}u)^{2}+(\unicode[STIX]{x2202}_{z}w)^{2}}{\Vert \unicode[STIX]{x1D64E}\Vert },\quad b_{12}=\frac{d^{2}M(\unicode[STIX]{x1D719})}{2\unicode[STIX]{x1D719}\unicode[STIX]{x1D6F9}^{2}(\unicode[STIX]{x1D719})}\frac{\unicode[STIX]{x2202}_{z}u\unicode[STIX]{x2202}_{z}w}{\Vert \unicode[STIX]{x1D64E}\Vert },\\ \displaystyle b_{21}=\frac{d^{2}M(\unicode[STIX]{x1D719})}{2\unicode[STIX]{x1D719}\unicode[STIX]{x1D6F9}^{2}(\unicode[STIX]{x1D719})}\frac{\unicode[STIX]{x2202}_{z}u\unicode[STIX]{x2202}_{z}w}{\Vert \unicode[STIX]{x1D64E}\Vert }-\frac{2d^{2}}{\unicode[STIX]{x1D719}\unicode[STIX]{x1D6F9}^{2}(\unicode[STIX]{x1D719})}\unicode[STIX]{x2202}_{z}u,\\ \displaystyle b_{22}=\frac{d^{2}M(\unicode[STIX]{x1D719})}{2\unicode[STIX]{x1D719}\unicode[STIX]{x1D6F9}^{2}(\unicode[STIX]{x1D719})}\frac{(\unicode[STIX]{x2202}_{z}u)^{2}+2(\unicode[STIX]{x2202}_{z}w)^{2}}{\Vert \unicode[STIX]{x1D64E}\Vert }-\frac{2d^{2}}{\unicode[STIX]{x1D719}\unicode[STIX]{x1D6F9}^{2}(\unicode[STIX]{x1D719})}\unicode[STIX]{x2202}_{z}w,\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle a_{1}=\frac{2d^{2}}{\unicode[STIX]{x1D719}}\unicode[STIX]{x2202}_{z}u\Vert \unicode[STIX]{x1D64E}\Vert \unicode[STIX]{x2202}_{\unicode[STIX]{x1D719}}\left(\frac{M(\unicode[STIX]{x1D719})}{\unicode[STIX]{x1D6F9}^{2}(\unicode[STIX]{x1D719})}\right),\\ \displaystyle a_{2}=\frac{2d^{2}\Vert \unicode[STIX]{x1D64E}\Vert }{\unicode[STIX]{x1D719}}\left[\unicode[STIX]{x2202}_{z}w\unicode[STIX]{x2202}_{\unicode[STIX]{x1D719}}\left(\frac{M(\unicode[STIX]{x1D719})}{\unicode[STIX]{x1D6F9}^{2}(\unicode[STIX]{x1D719})}\right)-2\Vert \unicode[STIX]{x1D64E}\Vert \unicode[STIX]{x2202}_{\unicode[STIX]{x1D719}}\left(\frac{1}{\unicode[STIX]{x1D6F9}^{2}(\unicode[STIX]{x1D719})}\right)\right],\\ \displaystyle b_{11}=\frac{d^{2}M(\unicode[STIX]{x1D719})}{2\unicode[STIX]{x1D719}\unicode[STIX]{x1D6F9}^{2}(\unicode[STIX]{x1D719})}\frac{2(\unicode[STIX]{x2202}_{z}u)^{2}+(\unicode[STIX]{x2202}_{z}w)^{2}}{\Vert \unicode[STIX]{x1D64E}\Vert },\quad b_{12}=\frac{d^{2}M(\unicode[STIX]{x1D719})}{2\unicode[STIX]{x1D719}\unicode[STIX]{x1D6F9}^{2}(\unicode[STIX]{x1D719})}\frac{\unicode[STIX]{x2202}_{z}u\unicode[STIX]{x2202}_{z}w}{\Vert \unicode[STIX]{x1D64E}\Vert },\\ \displaystyle b_{21}=\frac{d^{2}M(\unicode[STIX]{x1D719})}{2\unicode[STIX]{x1D719}\unicode[STIX]{x1D6F9}^{2}(\unicode[STIX]{x1D719})}\frac{\unicode[STIX]{x2202}_{z}u\unicode[STIX]{x2202}_{z}w}{\Vert \unicode[STIX]{x1D64E}\Vert }-\frac{2d^{2}}{\unicode[STIX]{x1D719}\unicode[STIX]{x1D6F9}^{2}(\unicode[STIX]{x1D719})}\unicode[STIX]{x2202}_{z}u,\\ \displaystyle b_{22}=\frac{d^{2}M(\unicode[STIX]{x1D719})}{2\unicode[STIX]{x1D719}\unicode[STIX]{x1D6F9}^{2}(\unicode[STIX]{x1D719})}\frac{(\unicode[STIX]{x2202}_{z}u)^{2}+2(\unicode[STIX]{x2202}_{z}w)^{2}}{\Vert \unicode[STIX]{x1D64E}\Vert }-\frac{2d^{2}}{\unicode[STIX]{x1D719}\unicode[STIX]{x1D6F9}^{2}(\unicode[STIX]{x1D719})}\unicode[STIX]{x2202}_{z}w,\end{array}\right\}\end{eqnarray}$$
where all values are evaluated with the base-state fields
From (A 10) and (A 5) it follows that
and
The two roots in (A 9) are real since
Since
![]() $\unicode[STIX]{x1D706}_{+}\sim \unicode[STIX]{x1D6EC}_{+}\unicode[STIX]{x1D709}^{2}$
as
$\unicode[STIX]{x1D706}_{+}\sim \unicode[STIX]{x1D6EC}_{+}\unicode[STIX]{x1D709}^{2}$
as
![]() $\unicode[STIX]{x1D709}\rightarrow \infty$
, the system is linearly ill-posed if the larger root
$\unicode[STIX]{x1D709}\rightarrow \infty$
, the system is linearly ill-posed if the larger root
![]() $\unicode[STIX]{x1D6EC}_{+}$
is positive, which occurs if either
$\unicode[STIX]{x1D6EC}_{+}$
is positive, which occurs if either
It may be seen from (A 12) and (A 13) that if
![]() $\text{tr}\,\unicode[STIX]{x1D71E}<0$
then
$\text{tr}\,\unicode[STIX]{x1D71E}<0$
then
![]() $\det \unicode[STIX]{x1D71E}<0$
, so it suffices to consider only case (b). Thus,
$\det \unicode[STIX]{x1D71E}<0$
, so it suffices to consider only case (b). Thus,
is a sufficient condition for ill-posedness.
Conversely, suppose
Then
![]() $\text{tr}\,\unicode[STIX]{x1D71E}$
and
$\text{tr}\,\unicode[STIX]{x1D71E}$
and
![]() $\det \unicode[STIX]{x1D71E}$
are both positive, so
$\det \unicode[STIX]{x1D71E}$
are both positive, so
![]() $\unicode[STIX]{x1D6EC}_{\pm }$
are both negative, and hence
$\unicode[STIX]{x1D6EC}_{\pm }$
are both negative, and hence
![]() $\unicode[STIX]{x1D706}_{\pm }\sim \unicode[STIX]{x1D6EC}_{\pm }\unicode[STIX]{x1D709}^{2}$
are bounded above. From (A 4), the third eigenvalue
$\unicode[STIX]{x1D706}_{\pm }\sim \unicode[STIX]{x1D6EC}_{\pm }\unicode[STIX]{x1D709}^{2}$
are bounded above. From (A 4), the third eigenvalue
![]() $\unicode[STIX]{x1D706}_{0}$
asymptotes to
$\unicode[STIX]{x1D706}_{0}$
asymptotes to
![]() $-C/B$
as
$-C/B$
as
![]() $\unicode[STIX]{x1D709}\rightarrow \infty$
. But
$\unicode[STIX]{x1D709}\rightarrow \infty$
. But
![]() $C/B$
is the ratio of two quartics and
$C/B$
is the ratio of two quartics and
![]() $B\neq 0$
since
$B\neq 0$
since
![]() $\det \unicode[STIX]{x1D71E}\neq 0$
. Thus
$\det \unicode[STIX]{x1D71E}\neq 0$
. Thus
![]() $\unicode[STIX]{x1D706}_{0}$
also remains bounded as
$\unicode[STIX]{x1D706}_{0}$
also remains bounded as
![]() $\unicode[STIX]{x1D709}\rightarrow \infty$
. In other words, (A 17) is a sufficient condition for well-posedness.
$\unicode[STIX]{x1D709}\rightarrow \infty$
. In other words, (A 17) is a sufficient condition for well-posedness.
To rewrite (A 16), (A 17) in a way that is useful for the computations in § 3.2, let us define
The one-dimensional computations with
![]() $\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology will be
$\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology will be
Appendix B. Positive stress power and Onsager symmetry
Goddard & Lee (Reference Goddard and Lee2018) examined equations for granular flow in light of Edelen’s (Reference Edelen1972) theory of irreversibility. They showed that the model of Heyman et al. (Reference Heyman, Delannay, Tabuteau and Valance2017), which includes
![]() $\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology, is not Onsager symmetric and not even properly dissipative. In this appendix the iCIDR equations are shown to have positive stress power and Onsager symmetry.
$\unicode[STIX]{x1D707}(I),\unicode[STIX]{x1D6F7}(I)$
-rheology, is not Onsager symmetric and not even properly dissipative. In this appendix the iCIDR equations are shown to have positive stress power and Onsager symmetry.
Positive-definite stress power means that all deformations with non-zero stress dissipate energy; i.e. in symbols, the dissipation rate
![]() ${\mathcal{D}}$
satisfies
${\mathcal{D}}$
satisfies
Using the decompositions of the stress (2.3) and the strain rate (2.5)
and it follows that
Substituting the alignment condition (2.6) and the dilatancy law (4.2) and recalling that
![]() $\Vert \unicode[STIX]{x1D64E}\Vert ^{2}=\text{tr}(\unicode[STIX]{x1D64E}^{2})/2$
, implies that
$\Vert \unicode[STIX]{x1D64E}\Vert ^{2}=\text{tr}(\unicode[STIX]{x1D64E}^{2})/2$
, implies that
The yield condition (4.1), the yield function (4.7) and the dilatancy function (4.8) then imply that the dissipation rate is
where
![]() $M=\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D719}))$
and
$M=\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D719}))$
and
![]() $\unicode[STIX]{x1D6F9}=\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D719})$
. Thus, the dissipation rate is non-negative and in fact positive if
$\unicode[STIX]{x1D6F9}=\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D719})$
. Thus, the dissipation rate is non-negative and in fact positive if
![]() $\Vert \unicode[STIX]{x1D64E}\Vert >0$
(and hence, by (4.12),
$\Vert \unicode[STIX]{x1D64E}\Vert >0$
(and hence, by (4.12),
![]() $p>0$
). To determine what happens when
$p>0$
). To determine what happens when
![]() $\Vert \unicode[STIX]{x1D64E}\Vert =0$
, the definition of the inertial number (2.9) is substituted into (B 5) to show that
$\Vert \unicode[STIX]{x1D64E}\Vert =0$
, the definition of the inertial number (2.9) is substituted into (B 5) to show that
As before, of course,
![]() ${\mathcal{D}}>0$
if
${\mathcal{D}}>0$
if
![]() $\Vert \unicode[STIX]{x1D64E}\Vert >0$
. If
$\Vert \unicode[STIX]{x1D64E}\Vert >0$
. If
![]() $\Vert \unicode[STIX]{x1D64E}\Vert =0$
but
$\Vert \unicode[STIX]{x1D64E}\Vert =0$
but
![]() $\text{div}\,\boldsymbol{u}<0$
, then by (4.12) the second term in (B 6) is positive. If
$\text{div}\,\boldsymbol{u}<0$
, then by (4.12) the second term in (B 6) is positive. If
![]() $\Vert \unicode[STIX]{x1D64E}\Vert =0$
but
$\Vert \unicode[STIX]{x1D64E}\Vert =0$
but
![]() $\text{div}\,\boldsymbol{u}>0$
, then indeed
$\text{div}\,\boldsymbol{u}>0$
, then indeed
![]() ${\mathcal{D}}=0$
, but
${\mathcal{D}}=0$
, but
![]() $p=0$
and by (4.14)
$p=0$
and by (4.14)
![]() $\Vert \unicode[STIX]{x1D749}\Vert =0$
, so
$\Vert \unicode[STIX]{x1D749}\Vert =0$
, so
![]() $\Vert \unicode[STIX]{x1D748}\Vert =0$
. This completes the verification of (B 1), i.e. the iCIDR equations always dissipate energy provided there is some deformation and the stresses are non-zero.
$\Vert \unicode[STIX]{x1D748}\Vert =0$
. This completes the verification of (B 1), i.e. the iCIDR equations always dissipate energy provided there is some deformation and the stresses are non-zero.
Since the constitutive laws have positive stress power, it follows from Edelen (Reference Edelen1972) that (i) all deformations are irreversible and increase entropy, (ii) the iCIDR constitutive laws satisfy Onsager symmetry and (iii) each component
![]() $\unicode[STIX]{x1D70E}_{ij}$
of the stress equals the derivative of a convex dissipation potential
$\unicode[STIX]{x1D70E}_{ij}$
of the stress equals the derivative of a convex dissipation potential
![]() $\unicode[STIX]{x1D713}(\unicode[STIX]{x1D63F})$
with respect to
$\unicode[STIX]{x1D713}(\unicode[STIX]{x1D63F})$
with respect to
![]() $\unicode[STIX]{x1D60B}_{ij}$
. Regarding point (iii), it is convenient to derive
$\unicode[STIX]{x1D60B}_{ij}$
. Regarding point (iii), it is convenient to derive
![]() $\unicode[STIX]{x1D713}$
through its Legendre transform,
$\unicode[STIX]{x1D713}$
through its Legendre transform,
where
![]() $\unicode[STIX]{x1D6FF}$
is a shorter notation for
$\unicode[STIX]{x1D6FF}$
is a shorter notation for
![]() $\text{div}\,\boldsymbol{u}$
when it appears as a dummy variable. Consider the function
$\text{div}\,\boldsymbol{u}$
when it appears as a dummy variable. Consider the function
The claim is that the iCIDR constitutive relations can be expressed as the derivatives
The first relation implies
which, in light of (2.6), (4.1) and (4.7), verifies (B 9a ). Whilst the the second implies
which, in light of (4.2) and (4.8), verifies (B 9b
). The dissipation potential
![]() $\unicode[STIX]{x1D713}(\unicode[STIX]{x1D63F})$
is the inverse Legendre transform of
$\unicode[STIX]{x1D713}(\unicode[STIX]{x1D63F})$
is the inverse Legendre transform of
![]() $\unicode[STIX]{x1D711}$
, which may be written
$\unicode[STIX]{x1D711}$
, which may be written
where
![]() $P(\unicode[STIX]{x1D64E},\text{div}\,\boldsymbol{u})$
is the pressure given by (4.12). Mixing stress and strain-rate variables,
$P(\unicode[STIX]{x1D64E},\text{div}\,\boldsymbol{u})$
is the pressure given by (4.12). Mixing stress and strain-rate variables,
![]() $\unicode[STIX]{x1D713}$
can be calculated as a function of
$\unicode[STIX]{x1D713}$
can be calculated as a function of
![]() $\unicode[STIX]{x1D64E}$
and
$\unicode[STIX]{x1D64E}$
and
![]() $p$
by replacing
$p$
by replacing
![]() $P$
in (B 12) by
$P$
in (B 12) by
![]() $p$
and substituting (B 11) for
$p$
and substituting (B 11) for
![]() $\text{div}\,\boldsymbol{u}$
, which yields
$\text{div}\,\boldsymbol{u}$
, which yields
Observe that
a result that follows from the formula (Goddard & Lee Reference Goddard and Lee2018)
and the observation that
![]() ${\mathcal{D}}$
is homogeneous in
${\mathcal{D}}$
is homogeneous in
![]() $\unicode[STIX]{x1D63F}$
of degree 3. It is not proved directly that
$\unicode[STIX]{x1D63F}$
of degree 3. It is not proved directly that
![]() $\unicode[STIX]{x1D713}$
is convex, but rather the fact that the iCIDR constitutive relations are well-posed (Barker et al.
Reference Barker, Schaeffer, Shearer and Gray2017) is used to deduce this (Goddard & Lee Reference Goddard and Lee2018).
$\unicode[STIX]{x1D713}$
is convex, but rather the fact that the iCIDR constitutive relations are well-posed (Barker et al.
Reference Barker, Schaeffer, Shearer and Gray2017) is used to deduce this (Goddard & Lee Reference Goddard and Lee2018).
Appendix C. Details of the DEM calculations
Two-dimensional DEM simulations (Cundall & Strack Reference Cundall and Strack1979) were performed in a shear-box geometry, both to confirm the well-established steady behaviour and to explore transient flows. The domain is a rectangle in
![]() $(x,z)$
space, with all units non-dimensionalized with the scalings (3.12), such that
$(x,z)$
space, with all units non-dimensionalized with the scalings (3.12), such that
![]() $0\leqslant \hat{x}<\hat{L}$
and
$0\leqslant \hat{x}<\hat{L}$
and
![]() $0\leqslant \hat{z}<{\hat{H}}$
. Boundary conditions and the system size are then designed to suppress confinement effects so that the volume can be taken to be a representative bulk element. Periodicity is enforced in the
$0\leqslant \hat{z}<{\hat{H}}$
. Boundary conditions and the system size are then designed to suppress confinement effects so that the volume can be taken to be a representative bulk element. Periodicity is enforced in the
![]() $\hat{x}$
direction and Lees–Edwards boundary conditions (Lees & Edwards Reference Lees and Edwards1972) are applied at the bottom
$\hat{x}$
direction and Lees–Edwards boundary conditions (Lees & Edwards Reference Lees and Edwards1972) are applied at the bottom
![]() $\hat{z}=0$
and top
$\hat{z}=0$
and top
![]() $\hat{z}={\hat{H}}$
of the domain. There is no gravity applied to the system and the only driving is provided by the difference in horizontal velocity between the top and bottom
$\hat{z}={\hat{H}}$
of the domain. There is no gravity applied to the system and the only driving is provided by the difference in horizontal velocity between the top and bottom
![]() $V_{0}$
, as prescribed by the Lees–Edwards algorithm.
$V_{0}$
, as prescribed by the Lees–Edwards algorithm.
Details of the precise DEM simulation algorithm can be found in Otsuki & Hayakawa (Reference Otsuki and Hayakawa2011) as an identical method is employed here. Normal forces
![]() $\boldsymbol{f}^{(n)}$
between particles are calculated from a linear spring–dashpot arrangement with an associated spring constant
$\boldsymbol{f}^{(n)}$
between particles are calculated from a linear spring–dashpot arrangement with an associated spring constant
![]() $k^{(n)}$
and viscous dissipation constant
$k^{(n)}$
and viscous dissipation constant
![]() $\unicode[STIX]{x1D702}^{(n)}$
. Tangential forces
$\unicode[STIX]{x1D702}^{(n)}$
. Tangential forces
![]() $\boldsymbol{f}^{(t)}$
may either stick or slip depending on whether a Coulomb friction criterion, with particle friction constant
$\boldsymbol{f}^{(t)}$
may either stick or slip depending on whether a Coulomb friction criterion, with particle friction constant
![]() $\unicode[STIX]{x1D707}_{p}$
, is satisfied. Stick interactions are defined as those with
$\unicode[STIX]{x1D707}_{p}$
, is satisfied. Stick interactions are defined as those with
![]() $|\boldsymbol{f}^{(t)}|<\unicode[STIX]{x1D707}_{p}|\boldsymbol{f}^{(n)}|$
and, like the normal force, are calculated from a linear spring–dashpot with parameters
$|\boldsymbol{f}^{(t)}|<\unicode[STIX]{x1D707}_{p}|\boldsymbol{f}^{(n)}|$
and, like the normal force, are calculated from a linear spring–dashpot with parameters
![]() $k^{(t)}$
and
$k^{(t)}$
and
![]() $\unicode[STIX]{x1D702}^{(t)}$
. Interactions with greater computed tangential forces are labelled as slip events and the tangential force is truncated to
$\unicode[STIX]{x1D702}^{(t)}$
. Interactions with greater computed tangential forces are labelled as slip events and the tangential force is truncated to
![]() $|\boldsymbol{f}^{(t)}|=\unicode[STIX]{x1D707}_{p}|\boldsymbol{f}^{(n)}|$
. In this paper parameters are chosen which give
$|\boldsymbol{f}^{(t)}|=\unicode[STIX]{x1D707}_{p}|\boldsymbol{f}^{(n)}|$
. In this paper parameters are chosen which give
![]() $k^{(n)}/p>10^{4}$
so that calculations are in the rigid particle regime of da Cruz et al. (Reference da Cruz, Emam, Prochnow, Roux and Chevoir2005). Unless stated otherwise the values
$k^{(n)}/p>10^{4}$
so that calculations are in the rigid particle regime of da Cruz et al. (Reference da Cruz, Emam, Prochnow, Roux and Chevoir2005). Unless stated otherwise the values
![]() $\unicode[STIX]{x1D707}_{p}=0.4$
,
$\unicode[STIX]{x1D707}_{p}=0.4$
,
![]() $k^{(n)}=10^{4}$
and
$k^{(n)}=10^{4}$
and
![]() $k^{(t)}=0.5k^{(n)}$
are used. Particle interactions with these values are very short-lived so that results are invariant of the viscous dissipation. The tangential dashpot is therefore neglected (
$k^{(t)}=0.5k^{(n)}$
are used. Particle interactions with these values are very short-lived so that results are invariant of the viscous dissipation. The tangential dashpot is therefore neglected (
![]() $\unicode[STIX]{x1D702}^{(t)}=0$
) and
$\unicode[STIX]{x1D702}^{(t)}=0$
) and
![]() $\unicode[STIX]{x1D702}^{(n)}=4.2$
is chosen, as in Silbert et al. (Reference Silbert, Ertaş, Grest, Halsey, Levine and Plimpton2001), so that the particles have a restitution coefficient of
$\unicode[STIX]{x1D702}^{(n)}=4.2$
is chosen, as in Silbert et al. (Reference Silbert, Ertaş, Grest, Halsey, Levine and Plimpton2001), so that the particles have a restitution coefficient of
![]() $e=0.9$
.
$e=0.9$
.
To select a mean packing fraction
![]() $\unicode[STIX]{x1D719}_{0}$
, the system size along the
$\unicode[STIX]{x1D719}_{0}$
, the system size along the
![]() $\hat{x}$
direction is determined as
$\hat{x}$
direction is determined as
![]() $L=\bar{A}N/(H\unicode[STIX]{x1D719}_{0})$
, where
$L=\bar{A}N/(H\unicode[STIX]{x1D719}_{0})$
, where
![]() $\bar{A}$
is the average grain area. The shear cell is then populated with
$\bar{A}$
is the average grain area. The shear cell is then populated with
![]() $N$
particles with density
$N$
particles with density
![]() $\unicode[STIX]{x1D70C}_{\ast }$
and mean diameter
$\unicode[STIX]{x1D70C}_{\ast }$
and mean diameter
![]() $d$
and
$d$
and
![]() $V_{0}$
set to unity in order to match the non-dimensional iCIDR equations. In order to avoid crystallization effects, the individual particle diameters are chosen randomly from a discretized distribution. Here an even spread from
$V_{0}$
set to unity in order to match the non-dimensional iCIDR equations. In order to avoid crystallization effects, the individual particle diameters are chosen randomly from a discretized distribution. Here an even spread from
![]() $0.8d$
,
$0.8d$
,
![]() $0.9d$
,
$0.9d$
,
![]() $d$
,
$d$
,
![]() $1.1d$
and
$1.1d$
and
![]() $1.2d$
is taken so that the number of particles of each diameter is
$1.2d$
is taken so that the number of particles of each diameter is
![]() $N/5$
. These particles, which are initially elastic but not frictional, are randomly distributed in the domain. This results in overlaps which would normally cause very large elastic forces, so firstly there is a period during which the total kinetic energy of all particles is scaled to a small constant value so that the system can reach an equilibrium state. The arrangement which results from this procedure has almost uniform packing density and very small overlaps. Then, the interaction algorithm is altered so that the particles are approximately rigid (very large
$N/5$
. These particles, which are initially elastic but not frictional, are randomly distributed in the domain. This results in overlaps which would normally cause very large elastic forces, so firstly there is a period during which the total kinetic energy of all particles is scaled to a small constant value so that the system can reach an equilibrium state. The arrangement which results from this procedure has almost uniform packing density and very small overlaps. Then, the interaction algorithm is altered so that the particles are approximately rigid (very large
![]() $k^{(n)}$
) and frictional. The true simulation begins after the velocity fields are prescribed.
$k^{(n)}$
) and frictional. The true simulation begins after the velocity fields are prescribed.
The steady-state
![]() $\unicode[STIX]{x1D707}(I)$
and
$\unicode[STIX]{x1D707}(I)$
and
![]() $\unicode[STIX]{x1D6F7}(I)$
relations found in previous works (e.g. da Cruz et al.
Reference da Cruz, Emam, Prochnow, Roux and Chevoir2005) are first confirmed in order to obtain macroscopic rheological parameters. Both curves are derived from the same set of experiments in which the solids volume fractions
$\unicode[STIX]{x1D6F7}(I)$
relations found in previous works (e.g. da Cruz et al.
Reference da Cruz, Emam, Prochnow, Roux and Chevoir2005) are first confirmed in order to obtain macroscopic rheological parameters. Both curves are derived from the same set of experiments in which the solids volume fractions
![]() $\unicode[STIX]{x1D719}_{0}$
take values in the range
$\unicode[STIX]{x1D719}_{0}$
take values in the range
![]() $0.76$
–
$0.76$
–
![]() $0.8$
. This range is expected to lie in the inertial regime and, due to the
$0.8$
. This range is expected to lie in the inertial regime and, due to the
![]() $\unicode[STIX]{x1D6F7}(I)$
relation, each packing corresponds to a unique inertial number. Once the system has reached a steady state, the flow fields are coarse-grained. This is achieved by averaging in the
$\unicode[STIX]{x1D6F7}(I)$
relation, each packing corresponds to a unique inertial number. Once the system has reached a steady state, the flow fields are coarse-grained. This is achieved by averaging in the
![]() $\hat{x}$
direction and then averaging within bins which discretize
$\hat{x}$
direction and then averaging within bins which discretize
![]() $\hat{z}$
into boxes of height
$\hat{z}$
into boxes of height
![]() $2d$
. Each run is then repeated 10 times in order to calculate error estimates. The solids volume fraction
$2d$
. Each run is then repeated 10 times in order to calculate error estimates. The solids volume fraction
![]() $\unicode[STIX]{x1D719}$
and the two velocity components
$\unicode[STIX]{x1D719}$
and the two velocity components
![]() $\hat{u}$
and
$\hat{u}$
and
![]() ${\hat{w}}$
are clearly defined in the DEM data and allow the inertial number to be readily calculated from its definition (1.1). Calculation of the bulk friction coefficient
${\hat{w}}$
are clearly defined in the DEM data and allow the inertial number to be readily calculated from its definition (1.1). Calculation of the bulk friction coefficient
![]() $\unicode[STIX]{x1D707}$
requires the macroscopic stress components to be defined. As in Silbert et al. (Reference Silbert, Ertaş, Grest, Halsey, Levine and Plimpton2001) this involves a sum over all particles
$\unicode[STIX]{x1D707}$
requires the macroscopic stress components to be defined. As in Silbert et al. (Reference Silbert, Ertaş, Grest, Halsey, Levine and Plimpton2001) this involves a sum over all particles
![]() $\unicode[STIX]{x1D6FC}$
in the sampling volume:
$\unicode[STIX]{x1D6FC}$
in the sampling volume:
where
![]() $\boldsymbol{r}^{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
is the centre-to-centre vector,
$\boldsymbol{r}^{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
is the centre-to-centre vector,
![]() $\boldsymbol{f}^{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
is the total force between particle pairs and
$\boldsymbol{f}^{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
is the total force between particle pairs and
![]() $\unicode[STIX]{x1D6FF}\hat{\boldsymbol{u}}^{\unicode[STIX]{x1D6FC}}=(\hat{u} ^{\unicode[STIX]{x1D6FC}}-\hat{V}_{0}\hat{z}/{\hat{H}},{\hat{w}}^{\unicode[STIX]{x1D6FC}})$
is the velocity fluctuation of particle
$\unicode[STIX]{x1D6FF}\hat{\boldsymbol{u}}^{\unicode[STIX]{x1D6FC}}=(\hat{u} ^{\unicode[STIX]{x1D6FC}}-\hat{V}_{0}\hat{z}/{\hat{H}},{\hat{w}}^{\unicode[STIX]{x1D6FC}})$
is the velocity fluctuation of particle
![]() $\unicode[STIX]{x1D6FC}$
. From the stress decomposition (2.3) these stress components are used to calculate the pressure
$\unicode[STIX]{x1D6FC}$
. From the stress decomposition (2.3) these stress components are used to calculate the pressure
![]() $p$
, deviatoric stress
$p$
, deviatoric stress
![]() $\Vert \unicode[STIX]{x1D749}\Vert$
and hence
$\Vert \unicode[STIX]{x1D749}\Vert$
and hence
![]() $\unicode[STIX]{x1D707}$
across the domain. As these quantities are all found to be invariant of
$\unicode[STIX]{x1D707}$
across the domain. As these quantities are all found to be invariant of
![]() $\hat{z}$
, the mean value is taken for the
$\hat{z}$
, the mean value is taken for the
![]() $\unicode[STIX]{x1D707}(I)$
data presented in figure 1(a). The volume fraction is also found to be constant at steady state so that the
$\unicode[STIX]{x1D707}(I)$
data presented in figure 1(a). The volume fraction is also found to be constant at steady state so that the
![]() $\unicode[STIX]{x1D6F7}(I)$
relation, plotted in figure 1(b), is simply verified using the mean packing density
$\unicode[STIX]{x1D6F7}(I)$
relation, plotted in figure 1(b), is simply verified using the mean packing density
![]() $\unicode[STIX]{x1D6F7}=\unicode[STIX]{x1D719}_{0}$
.
$\unicode[STIX]{x1D6F7}=\unicode[STIX]{x1D719}_{0}$
.