Article contents
Comparison of turbulent boundary layers over smooth and rough surfaces up to high Reynolds numbers
Published online by Cambridge University Press: 14 April 2016
Abstract
Turbulent boundary layer measurements above a smooth wall and sandpaper roughness are presented across a wide range of friction Reynolds numbers, 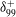 ${\it\delta}_{99}^{+}$, and equivalent sand grain roughness Reynolds numbers,
${\it\delta}_{99}^{+}$, and equivalent sand grain roughness Reynolds numbers, 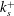 $k_{s}^{+}$ (smooth wall:
$k_{s}^{+}$ (smooth wall: 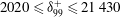 $2020\leqslant {\it\delta}_{99}^{+}\leqslant 21\,430$, rough wall:
$2020\leqslant {\it\delta}_{99}^{+}\leqslant 21\,430$, rough wall: 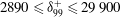 $2890\leqslant {\it\delta}_{99}^{+}\leqslant 29\,900$;
$2890\leqslant {\it\delta}_{99}^{+}\leqslant 29\,900$; 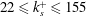 $22\leqslant k_{s}^{+}\leqslant 155$; and
$22\leqslant k_{s}^{+}\leqslant 155$; and 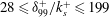 $28\leqslant {\it\delta}_{99}^{+}/k_{s}^{+}\leqslant 199$). For the rough-wall measurements, the mean wall shear stress is determined using a floating element drag balance. All smooth- and rough-wall data exhibit, over an inertial sublayer, regions of logarithmic dependence in the mean velocity and streamwise velocity variance. These logarithmic slopes are apparently the same between smooth and rough walls, indicating similar dynamics are present in this region. The streamwise mean velocity defect and skewness profiles each show convincing collapse in the outer region of the flow, suggesting that Townsend’s (The Structure of Turbulent Shear Flow, vol. 1, 1956, Cambridge University Press.) wall-similarity hypothesis is a good approximation for these statistics even at these finite friction Reynolds numbers. Outer-layer collapse is also observed in the rough-wall streamwise velocity variance, but only for flows with
$28\leqslant {\it\delta}_{99}^{+}/k_{s}^{+}\leqslant 199$). For the rough-wall measurements, the mean wall shear stress is determined using a floating element drag balance. All smooth- and rough-wall data exhibit, over an inertial sublayer, regions of logarithmic dependence in the mean velocity and streamwise velocity variance. These logarithmic slopes are apparently the same between smooth and rough walls, indicating similar dynamics are present in this region. The streamwise mean velocity defect and skewness profiles each show convincing collapse in the outer region of the flow, suggesting that Townsend’s (The Structure of Turbulent Shear Flow, vol. 1, 1956, Cambridge University Press.) wall-similarity hypothesis is a good approximation for these statistics even at these finite friction Reynolds numbers. Outer-layer collapse is also observed in the rough-wall streamwise velocity variance, but only for flows with 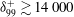 ${\it\delta}_{99}^{+}\gtrsim 14\,000$. At Reynolds numbers lower than this, profile invariance is only apparent when the flow is fully rough. In transitionally rough flows at low
${\it\delta}_{99}^{+}\gtrsim 14\,000$. At Reynolds numbers lower than this, profile invariance is only apparent when the flow is fully rough. In transitionally rough flows at low 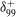 ${\it\delta}_{99}^{+}$, the outer region of the inner-normalised streamwise velocity variance indicates a dependence on
${\it\delta}_{99}^{+}$, the outer region of the inner-normalised streamwise velocity variance indicates a dependence on 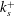 $k_{s}^{+}$ for the present rough surface.
$k_{s}^{+}$ for the present rough surface.
JFM classification
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
A correction has been issued for this article:
- 113
- Cited by
Linked content
Please note a has been issued for this article.



