Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Faure, Thierry M.
2014.
Velocity field and parametric analysis of a subsonic, medium-Reynolds number cavity flow.
Experiments in Fluids,
Vol. 55,
Issue. 11,
Basley, J.
Pastur, L. R.
Lusseyran, F.
Soria, J.
and
Delprat, N.
2014.
On the modulating effect of three-dimensional instabilities in open cavity flows.
Journal of Fluid Mechanics,
Vol. 759,
Issue. ,
p.
546.
de Vicente, J.
Basley, J.
Meseguer-Garrido, F.
Soria, J.
and
Theofilis, V.
2014.
Three-dimensional instabilities over a rectangular open cavity: from linear stability analysis to experimentation – ERRATUM.
Journal of Fluid Mechanics,
Vol. 751,
Issue. ,
p.
747.
Meseguer-Garrido, F.
de Vicente, J.
Valero, E.
and
Theofilis, V.
2014.
On linear instability mechanisms in incompressible open cavity flow.
Journal of Fluid Mechanics,
Vol. 752,
Issue. ,
p.
219.
Citro, Vincenzo
Giannetti, Flavio
Brandt, Luca
and
Luchini, Paolo
2015.
Linear three-dimensional global and asymptotic stability analysis of incompressible open cavity flow.
Journal of Fluid Mechanics,
Vol. 768,
Issue. ,
p.
113.
Liu, Q.
Gómez, F.
and
Theofilis, V.
2015.
Linear Instability Analysis of Incompressible Flow Over A Cuboid Cavity.
Procedia IUTAM,
Vol. 14,
Issue. ,
p.
511.
Theofilis, Vassilis
2015.
Special Issue on Instability and Control of Massively Separated Flows.
Aerospace Science and Technology,
Vol. 44,
Issue. ,
p.
1.
Lasagna, D.
and
Iuso, G.
2016.
Flow regimes in a trapped vortex cell.
Experiments in Fluids,
Vol. 57,
Issue. 3,
Liu, Qiong
Gómez, F.
Pérez, J.M.
and
Theofilis, V.
2016.
Instability and sensitivity analysis of flows using OpenFOAM®.
Chinese Journal of Aeronautics,
Vol. 29,
Issue. 2,
p.
316.
Liu, Qiong
Gómez, Francisco
and
Theofilis, Vassilios
2016.
Linear instability analysis of low- incompressible flow over a long rectangular finite-span open cavity.
Journal of Fluid Mechanics,
Vol. 799,
Issue. ,
Liu, Qiong
Gómez, Francisco
and
Theofilis, Vassilis
2016.
Control of flow instabilities in an open aircraft bay model cavity.
Beresh, Steven J.
Wagner, Justin L.
and
Casper, Katya M.
2016.
Compressibility effects in the shear layer over a rectangular cavity.
Journal of Fluid Mechanics,
Vol. 808,
Issue. ,
p.
116.
Beresh, Steven J.
Wagner, Justin L.
and
Casper, Katya M.
2016.
Compressibility Effects in the Shear Layer over a Rectangular Cavity.
Vinha, Nuno
Meseguer-Garrido, Fernando
de Vicente, Javier
and
Valero, Eusebio
2016.
A numerical study of the saturation process in an open cavity flow.
Vinha, N.
Meseguer-Garrido, F.
de Vicente, J.
and
Valero, E.
2016.
A dynamic mode decomposition of the saturation process in the open cavity flow.
Aerospace Science and Technology,
Vol. 52,
Issue. ,
p.
198.
Demauro, Edward P.
Beresh, Steven J.
Wagner, Justin L.
Henfling, John
and
Spillers, Russell
2016.
Three-Dimensional Measurement of Edge Effects in Open Cavities of Finite-Span.
Tuerke, F.
Pastur, L. R.
Sciamarella, D.
Lusseyran, F.
and
Artana, G.
2017.
Experimental study of double-cavity flow.
Experiments in Fluids,
Vol. 58,
Issue. 7,
Sun, Yiyang
Taira, Kunihiko
Cattafesta, Louis N.
and
Ukeiley, Lawrence S.
2017.
Biglobal instabilities of compressible open-cavity flows.
Journal of Fluid Mechanics,
Vol. 826,
Issue. ,
p.
270.
Sun, Y.
Taira, K.
Cattafesta, L. N.
and
Ukeiley, L. S.
2017.
Spanwise effects on instabilities of compressible flow over a long rectangular cavity.
Theoretical and Computational Fluid Dynamics,
Vol. 31,
Issue. 5-6,
p.
555.
Qadri, Ubaid Ali
and
Schmid, Peter J.
2017.
Frequency selection mechanisms in the flow of a laminar boundary layer over a shallow cavity.
Physical Review Fluids,
Vol. 2,
Issue. 1,
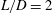 $L/D=2$ (length over depth) is conducted. This analysis is performed together with an experimental study in the same geometry adding spanwise endwalls. Two different Reynolds numbers are investigated through spectral analyses and modal decomposition. The physics of the flow is thoroughly described exploiting the strengths of each methodology. The main flow structures are identified and salient space and time scales are characterised. Results indicate that the structures obtained from linear analysis are mainly consistent with the fully saturated experimental flow. The analysis also brings to light the selection and alteration of certain wave properties, which could be caused by nonlinearities or the change of spanwise boundary conditions.
$L/D=2$ (length over depth) is conducted. This analysis is performed together with an experimental study in the same geometry adding spanwise endwalls. Two different Reynolds numbers are investigated through spectral analyses and modal decomposition. The physics of the flow is thoroughly described exploiting the strengths of each methodology. The main flow structures are identified and salient space and time scales are characterised. Results indicate that the structures obtained from linear analysis are mainly consistent with the fully saturated experimental flow. The analysis also brings to light the selection and alteration of certain wave properties, which could be caused by nonlinearities or the change of spanwise boundary conditions.

