Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Pasche, Simon
Gallaire, François
Dreyer, Matthieu
and
Farhat, Mohamed
2014.
Obstacle-induced spiral vortex breakdown.
Experiments in Fluids,
Vol. 55,
Issue. 8,
Juniper, Matthew P.
and
Pier, Benoit
2015.
The structural sensitivity of open shear flows calculated with a local stability analysis.
European Journal of Mechanics - B/Fluids,
Vol. 49,
Issue. ,
p.
426.
Chen, Kevin K.
Rowley, Clarence W.
and
Stone, Howard A.
2015.
Vortex dynamics in a pipe T-junction: Recirculation and sensitivity.
Physics of Fluids,
Vol. 27,
Issue. 3,
Canepa, E.
Cattanei, A.
Lengani, D.
Ubaldi, M.
and
Zunino, P.
2015.
Experimental investigation of the vortex breakdown in a lean premixing prevaporizing burner.
Journal of Fluid Mechanics,
Vol. 768,
Issue. ,
Miranda-Barea, A.
Martínez-Arias, B.
Parras, L.
Burgos, M. A.
and
del Pino, C.
2015.
Experimental study of rotating Hagen-Poiseuille flow discharging into a 1:8 sudden expansion.
Physics of Fluids,
Vol. 27,
Issue. 3,
Oberleithner, Kilian
Stöhr, Michael
Im, Seong Ho
Arndt, Christoph M.
and
Steinberg, Adam M.
2015.
Formation and flame-induced suppression of the precessing vortex core in a swirl combustor: Experiments and linear stability analysis.
Combustion and Flame,
Vol. 162,
Issue. 8,
p.
3100.
Camarri, Simone
2015.
Flow control design inspired by linear stability analysis.
Acta Mechanica,
Vol. 226,
Issue. 4,
p.
979.
Rukes, Lothar
Sieber, Moritz
Paschereit, C. Oliver
and
Oberleithner, Kilian
2016.
The impact of heating the breakdown bubble on the global mode of a swirling jet: Experiments and linear stability analysis.
Physics of Fluids,
Vol. 28,
Issue. 10,
Tammisola, O.
and
Juniper, M. P.
2016.
Coherent structures in a swirl injector at Re = 4800 by nonlinear simulations and linear global modes.
Journal of Fluid Mechanics,
Vol. 792,
Issue. ,
p.
620.
Chen, Kevin K.
and
Spedding, Geoffrey R.
2017.
Boussinesq global modes and stability sensitivity, with applications to stratified wakes.
Journal of Fluid Mechanics,
Vol. 812,
Issue. ,
p.
1146.
Grimble, T. A.
Agarwal, A.
and
Juniper, M. P.
2017.
Local linear stability analysis of cyclone separators.
Journal of Fluid Mechanics,
Vol. 816,
Issue. ,
p.
507.
Viola, F.
Pezzica, E.
Iungo, G. V.
Gallaire, F.
and
Camarri, S.
2017.
Flow control of weakly non-parallel flows: application to trailing vortices.
Journal of Fluid Mechanics,
Vol. 822,
Issue. ,
p.
342.
Rusak, Zvi
Zhang, Yuxin
Lee, Harry
and
Wang, Shixiao
2017.
Swirling flow states in finite-length diverging or contracting circular pipes.
Journal of Fluid Mechanics,
Vol. 819,
Issue. ,
p.
678.
Rukes, Lothar
Sieber, Moritz
Paschereit, Christian Oliver
and
Oberleithner, Kilian
2017.
Transient evolution of the global mode in turbulent swirling jets: Experiments and modal stability analysis.
European Journal of Mechanics - B/Fluids,
Vol. 65,
Issue. ,
p.
98.
Passaggia, Pierre-Yves
Scotti, Alberto
and
White, Brian
2017.
Transition and turbulence in horizontal convection: linear stability analysis.
Journal of Fluid Mechanics,
Vol. 821,
Issue. ,
p.
31.
Pasche, Simon
Avellan, François
and
Gallaire, François
2017.
Part Load Vortex Rope as a Global Unstable Mode.
Journal of Fluids Engineering,
Vol. 139,
Issue. 5,
Vanierschot, M.
2017.
On the dynamics of the transition to vortex breakdown in axisymmetric inviscid swirling flows.
European Journal of Mechanics - B/Fluids,
Vol. 65,
Issue. ,
p.
65.
Hiejima, Toshihiko
2017.
Streamwise vortex breakdown in supersonic flows.
Physics of Fluids,
Vol. 29,
Issue. 5,
Chterev, Ianko
Sundararajan, Gautham
Emerson, Ben
Seitzman, Jerry
and
Lieuwen, Tim
2017.
Precession Effects on the Relationship Between Time-Averaged and Instantaneous Reacting Flow Characteristics.
Combustion Science and Technology,
Vol. 189,
Issue. 2,
p.
248.
Chen, Kevin K.
Rowley, Clarence W.
and
Stone, Howard A.
2017.
Vortex breakdown, linear global instability and sensitivity of pipe bifurcation flows.
Journal of Fluid Mechanics,
Vol. 815,
Issue. ,
p.
257.
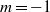 $m= - 1$ azimuthal mode is the most unstable and that the wavemaker regions of the
$m= - 1$ azimuthal mode is the most unstable and that the wavemaker regions of the 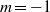 $m= - 1$ mode lie around the bubble, which is absolutely unstable. The mode is most sensitive to feedback involving the radial and azimuthal components of momentum in the region just upstream of the bubble. To a lesser extent, the mode is also sensitive to feedback involving the axial component of momentum in regions of high shear around the bubble. At an intermediate swirl, in which the bubble and wake have similar absolute growth rates, other researchers have found that the wavemaker of the nonlinear global mode lies in the wake. We agree with their analysis but find that the regions around the bubble are more influential than the wake in determining the growth rate and frequency of the linear global mode. The results from this paper provide the first steps towards passive control strategies for spiral vortex breakdown.
$m= - 1$ mode lie around the bubble, which is absolutely unstable. The mode is most sensitive to feedback involving the radial and azimuthal components of momentum in the region just upstream of the bubble. To a lesser extent, the mode is also sensitive to feedback involving the axial component of momentum in regions of high shear around the bubble. At an intermediate swirl, in which the bubble and wake have similar absolute growth rates, other researchers have found that the wavemaker of the nonlinear global mode lies in the wake. We agree with their analysis but find that the regions around the bubble are more influential than the wake in determining the growth rate and frequency of the linear global mode. The results from this paper provide the first steps towards passive control strategies for spiral vortex breakdown.

