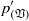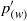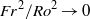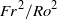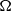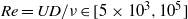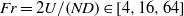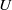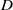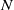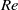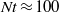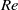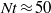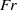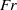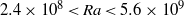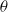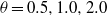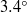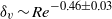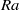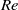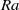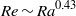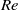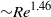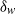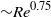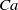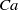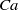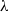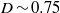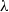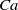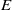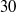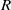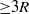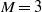Focus on Fluids
Three coins in a fountain
-
- Published online by Cambridge University Press:
- 05 March 2013, pp. 1-4
-
- Article
-
- You have access
- Export citation
Papers
The competition between gravity and flow focusing in two-layered porous media
-
- Published online by Cambridge University Press:
- 27 February 2013, pp. 5-14
-
- Article
- Export citation
Wall effects on pressure fluctuations in turbulent channel flow
-
- Published online by Cambridge University Press:
- 27 February 2013, pp. 15-65
-
- Article
- Export citation
The route to dissipation in strongly stratified and rotating flows
-
- Published online by Cambridge University Press:
- 27 February 2013, pp. 66-103
-
- Article
-
- You have access
- Open access
- Export citation
The internal gravity wave field emitted by a stably stratified turbulent wake
-
- Published online by Cambridge University Press:
- 27 February 2013, pp. 104-139
-
- Article
- Export citation
Viscous boundary layer properties in turbulent thermal convection in a cylindrical cell: the effect of cell tilting
-
- Published online by Cambridge University Press:
- 27 February 2013, pp. 140-168
-
- Article
- Export citation
Viscous drop in compressional Stokes flow
-
- Published online by Cambridge University Press:
- 27 February 2013, pp. 169-191
-
- Article
- Export citation
Investigation of sub-Kolmogorov inertial particle pair dynamics in turbulence using novel satellite particle simulations
-
- Published online by Cambridge University Press:
- 27 February 2013, pp. 192-211
-
- Article
- Export citation
The non-resonant response of fluid in a rapidly rotating sphere undergoing longitudinal libration
-
- Published online by Cambridge University Press:
- 27 February 2013, pp. 212-235
-
- Article
- Export citation
Structural organization of large and very large scales in turbulent pipe flow simulation
-
- Published online by Cambridge University Press:
- 27 February 2013, pp. 236-279
-
- Article
- Export citation
Lift and the leading-edge vortex
-
- Published online by Cambridge University Press:
- 27 February 2013, pp. 280-313
-
- Article
- Export citation
Gravity-driven granular free-surface flow around a circular cylinder
-
- Published online by Cambridge University Press:
- 27 February 2013, pp. 314-337
-
- Article
- Export citation
Flow domain identification from free surface velocity in thin inertial films
-
- Published online by Cambridge University Press:
- 27 February 2013, pp. 338-356
-
- Article
- Export citation
Rogue wave occurrence and dynamics by direct simulations of nonlinear wave-field evolution
-
- Published online by Cambridge University Press:
- 27 February 2013, pp. 357-392
-
- Article
- Export citation
Dynamical effect of the total strain induced by the coherent motion on local isotropy in a wake
-
- Published online by Cambridge University Press:
- 27 February 2013, pp. 393-423
-
- Article
- Export citation
Direct numerical simulation of the autoignition of a hydrogen plume in a turbulent coflow of hot air
-
- Published online by Cambridge University Press:
- 27 February 2013, pp. 424-456
-
- Article
- Export citation
Flow over a flat plate with uniform inlet and incident coherent gusts
-
- Published online by Cambridge University Press:
- 27 February 2013, pp. 457-485
-
- Article
- Export citation
Natural convection in horizontal pipe flow with a strong transverse magnetic field
-
- Published online by Cambridge University Press:
- 27 February 2013, pp. 486-516
-
- Article
- Export citation
Bending of elastic fibres in viscous flows: the influence of confinement‡
-
- Published online by Cambridge University Press:
- 27 February 2013, pp. 517-544
-
- Article
- Export citation
Wake and thrust of an angularly reciprocating plate
-
- Published online by Cambridge University Press:
- 27 February 2013, pp. 545-557
-
- Article
- Export citation