Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kim, Nayoung
Kim, Hyunseok
and
Park, Hyungmin
2015.
An experimental study on the effects of rough hydrophobic surfaces on the flow around a circular cylinder.
Physics of Fluids,
Vol. 27,
Issue. 8,
Kim, Minki
Lee, Jun Ho
and
Park, Hyungmin
2016.
Study of bubble-induced turbulence in upward laminar bubbly pipe flows measured with a two-phase particle image velocimetry.
Experiments in Fluids,
Vol. 57,
Issue. 4,
Dabiri, Sadegh
and
Bhuvankar, Pramod
2016.
Scaling law for bubbles rising near vertical walls.
Physics of Fluids,
Vol. 28,
Issue. 6,
Khadamkar, Hrushikesh P.
Patwardhan, Ashwin W.
and
Mathpati, Channamallikarjun S.
2017.
Computational Fluid Dynamics Simulations of Single Drops in Confined Geometries.
Industrial & Engineering Chemistry Research,
Vol. 56,
Issue. 29,
p.
8311.
Joshi, Jyeshtharaj B.
Nandakumar, K.
Evans, Geoffrey M.
Pareek, Vishnu K.
Gumulya, Monica M.
Sathe, Mayur J.
and
Khanwale, Makrand A.
2017.
Bubble generated turbulence and direct numerical simulations.
Chemical Engineering Science,
Vol. 157,
Issue. ,
p.
26.
Lee, Joohyoung
and
Park, Hyungmin
2017.
Wake structures behind an oscillating bubble rising close to a vertical wall.
International Journal of Multiphase Flow,
Vol. 91,
Issue. ,
p.
225.
Asiagbe, Kenneth S.
Fairweather, Michael
Njobuenwu, Derrick O.
and
Colombo, Marco
2017.
Large eddy simulation of microbubble transport in a turbulent horizontal channel flow.
International Journal of Multiphase Flow,
Vol. 94,
Issue. ,
p.
80.
Choi, Daehyun
and
Park, Hyungmin
2018.
Flow around in-line sphere array at moderate Reynolds number.
Physics of Fluids,
Vol. 30,
Issue. 9,
Kong, G
Mirsandi, H.
Buist, K. A.
Peters, E. A. J. F.
Baltussen, M. W.
and
Kuipers, J. A. M.
2019.
Hydrodynamic interaction of bubbles rising side-by-side in viscous liquids.
Experiments in Fluids,
Vol. 60,
Issue. 10,
Kim, Yewon
and
Park, Hyungmin
2019.
Upward bubbly flows in a square pipe with a sudden expansion: Bubble dispersion and reattachment length.
International Journal of Multiphase Flow,
Vol. 118,
Issue. ,
p.
254.
Kherbeche, Abderrahmane
Mei, Mei
Thoraval, Marie-Jean
Hébrard, Gilles
and
Dietrich, Nicolas
2020.
Hydrodynamics and gas-liquid mass transfer around a confined sliding bubble.
Chemical Engineering Journal,
Vol. 386,
Issue. ,
p.
121461.
Zhang, Yang
Dabiri, Sadegh
Chen, Ke
and
You, Yunxiang
2020.
An initially spherical bubble rising near a vertical wall.
International Journal of Heat and Fluid Flow,
Vol. 85,
Issue. ,
p.
108649.
Muniz, Marcelo
and
Sommerfeld, Martin
2020.
On the force competition in bubble columns: A numerical study.
International Journal of Multiphase Flow,
Vol. 128,
Issue. ,
p.
103256.
Tu, Chengxu
Yang, Qincan
Chen, Yeyu
Ye, Yuhang
Wang, Yukun
Du, Pengfei
Yang, Sensen
Bao, Fubing
Yin, Zhaoqin
Jiang, Renjie
and
Liang, Xiaoyu
2020.
Anisotropic Spreading of Bubbles on Superaerophilic Straight Trajectories beneath a Slide in Water.
Water,
Vol. 12,
Issue. 3,
p.
798.
Larachi, Faïçal
Schmidtchen, Clara
Haase, Stefan
and
Taghavi, Seyed Mohammad
2021.
Trajectory Analysis of Rising Spheroidal Bubbles in a Rolling Column.
ACS Engineering Au,
Vol. 1,
Issue. 2,
p.
105.
Park, Hyungmin
Choi, Chang-Hwan
and
Kim, Chang-Jin
2021.
Superhydrophobic drag reduction in turbulent flows: a critical review.
Experiments in Fluids,
Vol. 62,
Issue. 11,
Chen, Yeyu
Tu, Chengxu
Yang, Qincan
Wang, Yukun
Ye, Yuhang
Chen, Qiang
Jiang, Renjie
Yang, Meng
and
Bao, Fubing
2021.
Dynamic behavior of a deformable bubble rising near a vertical wire-mesh in the quiescent water.
Experimental Thermal and Fluid Science,
Vol. 120,
Issue. ,
p.
110235.
Lee, Jubeom
Kim, Min
and
Park, Hyungmin
2021.
Single-layer wire-mesh sensor to simultaneously measure the size and rise velocity of micro-to-millimeter sized bubbles in a gas-liquid two-phase flow.
International Journal of Multiphase Flow,
Vol. 139,
Issue. ,
p.
103620.
Choi, Kyuseong
and
Park, Hyungmin
2021.
Interfacial phenomena of the interaction between a liquid–liquid interface and rising bubble.
Experiments in Fluids,
Vol. 62,
Issue. 6,
Sirino, Thiago
Mancilla, Ernesto
and
Morales, Rigoberto E.M.
2021.
Experimental Study on the Behavior of Single Rising Bubbles in a Confined Rectangular Channel.
International Journal of Multiphase Flow,
Vol. 145,
Issue. ,
p.
103818.
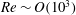 $\mathit{Re}\sim \mathit{O}(10^{3})$) rising near a vertical wall in quiescent water is experimentally investigated. The reference (without the wall) rising path of the considered bubble is a two-dimensional zigzag. For a range of wall configurations (i.e. initial wall distance and boundary condition), using high-speed shadowgraphy, various rising behaviours such as periodic bouncing, sliding, migrating away, and non-periodic oscillation without collisions are measured and analysed. Unlike low-Reynolds- and Weber-number bubbles, the contribution of the surface deformation to the transport between the energy components becomes significant during the bubble’s rise. In particular, across the bubble–wall collision, the excess surface energy compensates the deficit of kinetic energy. This enables a large deformable bubble to maintain a relatively constant bouncing kinematics, despite the obvious wall-induced energy dissipation. The wall effect, predominantly appearing as energy loss, is found to decrease as the initial distance from the bubble centre to the wall increases. Compared to the regular (no-slip) wall, a hydrophobic surface enhances or reduces the wall effect depending on the wall distance, whereas a porous surface reduces the energy loss due to the wall, regardless of the initial distance from the wall. Furthermore, the bubble–wall collision behaviour is assessed in terms of a restitution coefficient and modified impact Stokes number (ratio of the inertia to viscous forces), which shows a good correlation, the trends of which agree well with the variations in the energy components. The dependence of near-wall bubble motion on the wall distance and boundary condition may suggest a way of predicting or controlling the near-wall gas void-fraction distribution in gas–liquid flow systems.
$\mathit{Re}\sim \mathit{O}(10^{3})$) rising near a vertical wall in quiescent water is experimentally investigated. The reference (without the wall) rising path of the considered bubble is a two-dimensional zigzag. For a range of wall configurations (i.e. initial wall distance and boundary condition), using high-speed shadowgraphy, various rising behaviours such as periodic bouncing, sliding, migrating away, and non-periodic oscillation without collisions are measured and analysed. Unlike low-Reynolds- and Weber-number bubbles, the contribution of the surface deformation to the transport between the energy components becomes significant during the bubble’s rise. In particular, across the bubble–wall collision, the excess surface energy compensates the deficit of kinetic energy. This enables a large deformable bubble to maintain a relatively constant bouncing kinematics, despite the obvious wall-induced energy dissipation. The wall effect, predominantly appearing as energy loss, is found to decrease as the initial distance from the bubble centre to the wall increases. Compared to the regular (no-slip) wall, a hydrophobic surface enhances or reduces the wall effect depending on the wall distance, whereas a porous surface reduces the energy loss due to the wall, regardless of the initial distance from the wall. Furthermore, the bubble–wall collision behaviour is assessed in terms of a restitution coefficient and modified impact Stokes number (ratio of the inertia to viscous forces), which shows a good correlation, the trends of which agree well with the variations in the energy components. The dependence of near-wall bubble motion on the wall distance and boundary condition may suggest a way of predicting or controlling the near-wall gas void-fraction distribution in gas–liquid flow systems.


