Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-17T18:11:27.623Z Has data issue: false hasContentIssue false
  • English
  • Français

Dependence of wake structure on pitching frequency behind a thin panel at $Re=1000$

Published online by Cambridge University Press:  12 August 2021

Arnab Kumar De Open the ORCID record for Arnab Kumar De [Opens in a new window]  and
Sandip Sarkar Open the ORCID record for Sandip Sarkar [Opens in a new window]
Arnab Kumar De
Affiliation:
Department of Mechanical Engineering, Indian Institute of Technology Guwahati, Assam781039, India
Sandip Sarkar*
Affiliation:
Department of Mechanical Engineering, Jadavpur University, Kolkata700032, India
*
†Email addresses for correspondence: thesandipsarkar3@gmail.com, sandipsarkar.mech@jadavpuruniversity.in
Get access Rights & Permissions [Opens in a new window]

Abstract

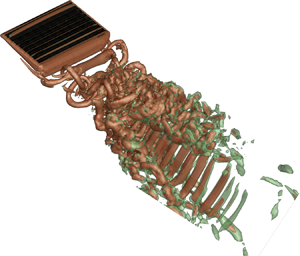
We perform computations of wake transition behind a pitching panel using an immersed boundary-based method. At a Reynolds number $Re=1000$, simulations are carried out over a wide range of pitching frequencies in the Strouhal number ($St$) range $0.2\leqslant St \leqslant 2$, for two different aspect ratio panels, given by 0.54 and 2.38. Our results reveal appearances of a reverse von Kármán vortex street at a moderate pitching frequency, which bifurcates into two distinct branches connected by strands at higher Strouhal number. In addition, the larger-aspect-ratio panel exhibits an avalanche of large, tangled three-dimensional vortex structures for $St\geqslant 1.5$. We observe strong spanwise wake compression, for the larger-aspect-ratio panel, greatly influencing the secondary instabilities at increased pitching frequency. However, no direct relationship between the growth of secondary instabilities and the spanwise pressure gradient can be established. We show that an increase in $St$ leads to a stable central region and renders a larger concentration of small-scale structures at the jet plane. The continuous wavelet transform shows complete synchronisation of the shed structure with the pitching Strouhal number of the low-aspect-ratio panel. The spectral characteristic for the high-aspect-ratio panel at $St=1$ is found to be dominated by a narrow band of low-frequency cells. We observed the period-doubling phenomena in the spanwise cells during space–time reconstruction of the velocity signals. For the present ranges of $St$, both thrust and lift signals reveal a constant amplitude oscillation, the latter being double, in magnitude, the former. Both root-mean-squared thrust and lift coefficients grow with $St$ and aspect ratio.

JFM classification

Aerodynamics: Flow-structure interactions Vortex Flows: Vortex dynamics Vortex Flows: Vortex shedding
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 924 , 10 October 2021 , A33
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Agarwal, A., Nolan, K.P., Stafford, J. & Jeffers, N. 2017 Visualization of three-dimensional structures shed by an oscillating beam. J. Fluids Struct. 70, 450–463.CrossRefGoogle Scholar
Anderson, J.M., Streitlien, K., Barrett, D.S. & Triantafyllou, M.S. 1998 Oscillating foils of high propulsive efficiency. J. Fluid Mech. 360, 41–72.CrossRefGoogle Scholar
Biswas, G. & Sarkar, S. 2009 Effect of thermal buoyancy on vortex shedding past a circular cylinder in cross-flow at low Reynolds numbers. Intl J. Heat Mass Transfer 52, 1897–1912.CrossRefGoogle Scholar
Blondeaux, P., Fornarelli, F., Guglielmini, L., Triantafyllou, M.S. & Verzicco, R. 2005 Numerical experiments on flapping foils mimicking fish-like locomotion. Phys. Fluids 17, 113601.CrossRefGoogle Scholar
Borazjani, I. & Sotiropoulos, F. 2008 Numerical investigation of the hydrodynamics of anguilliform swimming in the transitional and inertial flow regimes. J. Expl Biol. 212, 576–592.CrossRefGoogle Scholar
Borazjani, I. & Sotiropoulos, F. 2009 Vortex-induced vibrations of two cylinders in tandem arrangement in the proximity-wake interference region. J. Fluid Mech. 621, 321–364.CrossRefGoogle ScholarPubMed
Bose, C. & Sarkar, S. 2018 Investigating chaotic wake dynamics past a flapping airfoil and the role of vortex interactions behind the chaotic transition. Phys. Fluids 30, 047101.CrossRefGoogle Scholar
Buchholz, J.H.J. 2006 The flow field and performance of a low aspect ratio unsteady propulsor. PhD thesis, Princeton University.Google Scholar
Buchholz, J.H.J., Jimenez, J.M., Allen, J.J. & Smits, A.J. 2003 Hydrodynamics of thrust production in a fish-like flapping membrane. In 13th International Symposium on Unmanned Untethered Submersible Technology. University of New Hampshire, Durham, NH.Google Scholar
Buchholz, J.H.J. & Smits, A.J. 2006 On the evolution of the wake structure produced by a low-aspect-ratio pitching panel. J. Fluid Mech. 546, 433–443.CrossRefGoogle Scholar
Buchholz, J.H.J. & Smits, A.J. 2008 The wake structure and thrust performance of a rigid low-aspect-ratio pitching panel. J. Fluid Mech. 603, 331–365.CrossRefGoogle ScholarPubMed
Calderon, D.E., Cleaver, D.J., Gursul, I. & Wang, Z. 2014 On the absence of asymmetric wakes for periodically plunging finite wings. Phys. Fluids. 26, 071907.CrossRefGoogle Scholar
Clark, R.P. & Smits, A.J. 2006 Thrust production and wake structure of a batoid-inspired oscillating fin. J. Fluid Mech. 562, 415–429.CrossRefGoogle ScholarPubMed
Cleaver, D.J., Wang, Z. & Gursul, I. 2012 Bifurcating flows of plunging aerofoils at high Strouhal numbers. J. Fluid Mech. 708, 349–376.CrossRefGoogle Scholar
Dai, H., Luo, H., Ferreira de Sousa, P.J.S.A. & Doyle, J.F. 2012 Thrust performance of a flexible low-aspect-ratio pitching plate. Phys. Fluids 24, 101903.CrossRefGoogle Scholar
De, A.K. 2016 A diffuse interface immersed boundary method for convective heat and fluid flow. Intl J. Heat Mass Transfer 92, 957–969.CrossRefGoogle Scholar
De, A.K. 2018 A diffuse interface immersed boundary method for complex moving boundary problems. J. Comput. Phys. 366, 226–251.CrossRefGoogle Scholar
De, A.K. & Sarkar, S. 2020 a Three-dimensional wake dynamics behind a tapered cylinder with large taper ratio. Phys. Fluids 32, 063604.CrossRefGoogle Scholar
De, A.K. & Sarkar, S. 2020 b Wake events during early three-dimensional transition of a circular cylinder placed in shear flow. Phys. Fluids 32, 053603.CrossRefGoogle Scholar
Dewey, P.A., Carriou, A. & Smits, A.J. 2012 On the relationship between efficiency and wake structure of a batoid-inspired oscillating fin. J. Fluid Mech. 691, 245–266.CrossRefGoogle Scholar
Dhanak, M. & Bernardinis, B. 1981 The evolution of an elliptic vortex ring. J. Fluid Mech. 109, 189–216.CrossRefGoogle Scholar
Dong, H., Bozkurttas, M., Mittal, R., Madden, P. & Lauder, G.V. 2010 Computational modelling and analysis of the hydrodynamics of a highly deformable fish pectoral fin. J. Fluid Mech. 645, 345–373.CrossRefGoogle Scholar
Dong, H., Mittal, R. & Najjar, F.M. 2006 Wake topology and hydrodynamic performance of low-aspect-ratio flapping foils. J. Fluid Mech. 566, 309–343.CrossRefGoogle Scholar
Ebrahimi, N.D., Eldredge, J.D. & Ju, Y.S. 2020 Three-dimensional characteristics of the jet flows induced by a pitching plate in a quiescent fluid. J. Fluid Mech. 887, A25.CrossRefGoogle Scholar
von Ellenrieder, K.D., Parker, K. & Soria, J. 2003 Flow structures behind a heaving and pitching finite-span wing. J. Fluid Mech. 490, 129–138.CrossRefGoogle Scholar
Ellington, C.P. 1984 The aerodynamics of hovering insect flight. II. Morphological parameters. Phil. Trans. R. Soc. Lond. B 305, 17–40.Google Scholar
Fernandez-Prats, R. 2017 Effect of chordwise flexibility on pitching foil propulsion in a uniform current. Ocean Engng 145, 24–33.CrossRefGoogle Scholar
Fish, F., Schreiber, C., Moored, K., Liu, G., Dong, H. & Bart-Smith, H. 2016 Hydrodynamic performance of aquatic flapping: efficiency of underwater flight in the manta. Aerospace 3, 20.CrossRefGoogle Scholar
Freymuth, P. 1988 Propulsive vortical signature of plunging and pitching airfoils. AIAA J. 27 (9), 1200–1205.Google Scholar
Freymuth, P., Finaish, F. & Bank, W. 1987 Further visualization of combined wing tip and starting vortex systems. AIAA J. 25 (9), 1153–1159.CrossRefGoogle Scholar
Ghovardhan, R. & Williamson, C.H.K. 2005 Vortex-induced vibrations of a sphere. J. Fluid Mech. 531, 11–47.CrossRefGoogle Scholar
Green, M.A. & Smits, A.J. 2008 Effects of three-dimensionality on thrust production by a pitching panel. J. Fluid Mech. 615, 211–220.CrossRefGoogle ScholarPubMed
Guglielmini, L. 2004 Modeling of thrust generating foils. PhD thesis, University of Genoa.Google Scholar
Hemmati, A., Van Buren, T. & Smits, A.J. 2019 Effects of trailing edge shape on vortex formation by pitching panels of small aspect ratio. Phys. Rev. Fluids 4, 033101.CrossRefGoogle Scholar
Hultmark, M., Leftwich, M. & Smits, A.J. 2007 Flowfield measurements in the wake of a robotic lamprey. Exp. Fluids 43, 683–690.CrossRefGoogle ScholarPubMed
Jafari, P., Masoudi, A., Irajizad, P., Nazari, M., Kashyap, V., Eslami, B. & Ghasemi, H. 2018 Evaporation mass flux: a predictive model and experiments. Langmuir 34 (39), 11676–11684.CrossRefGoogle ScholarPubMed
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.CrossRefGoogle Scholar
Kim, D., Strom, B., Mandre, S. & Breuer, K. 2017 Energy harvesting performance and flow structure of an oscillating hydrofoil with finite span. J. Fluids Struct. 70, 314–326.CrossRefGoogle Scholar
Koochesfahani, M.M. 1989 Vortical patterns in the wake of an oscillating airfoil. AIAA J. 27, 1200–1205.CrossRefGoogle Scholar
Kushwaha, V.K.. & De, A.K. 2020 Aerodynamics of multiple freely falling plates. Phys. Fluids 32, 103603.CrossRefGoogle Scholar
Li, C. & Dong, H. 2016 Three-dimensional wake topology and propulsive performance of low-aspect-ratio pitching-rolling plates. Phys. Fluids 28, 071901.CrossRefGoogle Scholar
Li, G.-J. & Lu, X.-Y. 2012 Force and power of flapping plates in a fluid. J. Fluid Mech. 712, 598–613.CrossRefGoogle Scholar
Liang, Z. & Dong, H. 2015 On the symmetry of proper orthogonal decomposition modes of a low-aspect-ratio plate. Phys. Fluids 27, 063601.CrossRefGoogle Scholar
Nazari, M., Masoudi, A., Jafari, P., Irajizad, P., Kashyap, V. & Ghasemi, H. 2018 Ultrahigh evaporative heat fluxes in nanoconfined geometries. Langmuir 35 (1), 78–85.CrossRefGoogle ScholarPubMed
Oshima, Y. & Natsume, A. 1980 Flow field around an oscillating airfoil. In Flow Visualization II. Proceedings Second International Symposium on Flow Visualization, Bochum, W. Germany (ed. W. Merzkirch). Hemisphere.Google Scholar
Oshima, Y. & Oshima, K. 1980 Vortical flow behind an oscillating airfoil. In Proceedings 15th Congress, International Union of Theoretical and Applied Mechanics. North Holland.Google Scholar
Pan, D. & Shen, T.T. 2009 Computation of incompressible flows with immersed bodies by a simple ghost cell method. Intl J. Numer. Meth. Fluids 60, 1378–1401.CrossRefGoogle Scholar
Panah, A.E., Akkala, J.M. & Buchholz, J.H.J. 2013 Vortex dynamics of a finite-aspect-ratio plunging wing. In 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition 2013 – Grapevine, TX, United States. AIAA.Google Scholar
Prince, C., Lin, W., Lin, J., Peterson, S.D. & Porfiri, M. 2010 Temporally-resolved hydrodynamics in the vicinity of a vibrating ionic polymer metal composite. J. Appl. Phys. 107 (9), 094908.CrossRefGoogle Scholar
Richard, B. 1958 The speed of swimming of fish as related to size and to the frequency and amplitude of the tail beat. J. Expl Biol. 35, 109–133.Google Scholar
Ringuette, M.J., Milano, M. & Gharib, M. 2007 Role of the tip vortex in the force generation of low-aspect-ratio normal flat plates. J. Fluid Mech. 581, 453–468.CrossRefGoogle Scholar
Sarkar, S. & Venkatraman, K. 2006 Numerical simulation of thrust generating flow past a pitching airfoil. Comput. Fluids 35, 16–42.CrossRefGoogle Scholar
Taira, K. & Colonius, T. 2009 Three-dimensional flows around low-aspect-ratio flat-plate wings at low Reynolds numbers. J. Fluid Mech. 623, 187–207.CrossRefGoogle Scholar
Taylor, G., Nudds, R. & Thomas, A. 2003 Flying and swimming animals cruise at a Strouhal number tuned for high power efficiency. Nature 425, 707–711.CrossRefGoogle Scholar
Thekkethil, N., Sharma, A. & Agrawal, A. 2020 Three-dimensional biological hydrodynamics study on various types of batoid fishlike locomotion. Phys. Rev. Fluids 5, 023101.CrossRefGoogle Scholar
Torres, G.E. & Mueller, T.J. 2004 Low-aspect-ratio wing aerodynamics at low Reynolds numbers. AIAA J. 42 (5), 865–873.CrossRefGoogle Scholar
Triantafyllou, G.S., Triantafyllou, M.S. & Grosenbaugh, M.A. 1993 Optimal thrust development in oscillating foils with application to fish propulsion. J. Fluids Struct. 7, 205–224.CrossRefGoogle Scholar
Tytell, E.D. & Lauder, G.V. 2004 The hydrodynamics of eel swimming: I. Wake structure. J. Expl Biol. 207, 1825–1841.CrossRefGoogle ScholarPubMed
Virk, D., Hussain, F. & Kerr, R.M. 1995 Compressible vortex reconnection. J. Fluid Mech. 304, 47–86.CrossRefGoogle Scholar
Visbal, M., Yilmaz, T.O. & Rockwell, D. 2013 Three-dimensional vortex formation on a heaving low-aspect-ratio wing: computations and experiments. J. Fluids Struct. 38, 58–76.CrossRefGoogle Scholar
Visbal, M.R. 2009 High-fidelity simulation of transitional flows past a plunging airfoil. AIAA J. 47 (11), 2685–2697.CrossRefGoogle Scholar
Williamson, C.H.K. & Roshko, A. 1988 Vortex formation in the wake of an oscillating cylinder. J. Fluids Struct. 2, 355–381.CrossRefGoogle Scholar
Zhu, Q. & Shoele, K. 2008 Propulsion performance of a skeleton-strengthened fin. J. Expl Biol. 211, 2087–2100.CrossRefGoogle ScholarPubMed