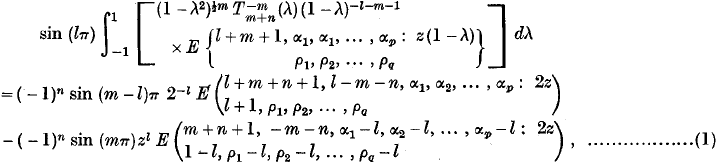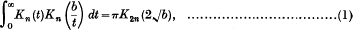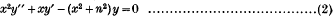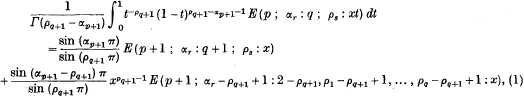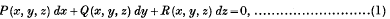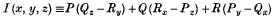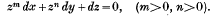Research Article
On the Theory of Relaxation
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 101-110
-
- Article
-
- You have access
- Export citation
An Integral involving an E-function and an Associated Legendre Function of the First Kind
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 111-114
-
- Article
-
- You have access
- Export citation
Generalisation of an Integral due to Hardy
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 115-117
-
- Article
-
- You have access
- Export citation
Integral of an E-function expressed as a Sum of two E-functions
-
- Published online by Cambridge University Press:
- 18 May 2009, p. 118
-
- Article
-
- You have access
- Export citation
An Integral involving a Modified Bessel Function of the Second Kind and an E-function
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 119-120
-
- Article
-
- You have access
- Export citation
The Product of Two Legendre Polynomials
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 121-125
-
- Article
-
- You have access
- Export citation
An Expression for Bernoulli Numbers
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 126-128
-
- Article
-
- You have access
- Export citation
Integrals involving E-functions
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 129-136
-
- Article
-
- You have access
- Export citation
Exceptional Integrals of a not completely Integrable Total Differential Equation
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 137-138
-
- Article
-
- You have access
- Export citation
The Equivalence of Asymptotic Distributions under Randomisation and Normal Theories
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 139-147
-
- Article
-
- You have access
- Export citation
Front matter
GMJ volume 1 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
GMJ volume 1 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation