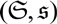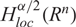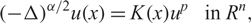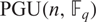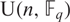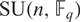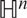Research Article
EXTENSIONS OF HILBERTIAN RINGS
- Part of:
-
- Published online by Cambridge University Press:
- 05 November 2018, pp. 1-11
-
- Article
- Export citation
CONFIGURATION CATEGORIES AND HOMOTOPY AUTOMORPHISMS
- Part of:
-
- Published online by Cambridge University Press:
- 19 November 2018, pp. 13-41
-
- Article
- Export citation
A CLASS OF QUASITRIANGULAR GROUP-COGRADED MULTIPLIER HOPF ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 20 December 2018, pp. 43-57
-
- Article
- Export citation
CONCERNING SUMMABLE SZLENK INDEX
- Part of:
-
- Published online by Cambridge University Press:
- 21 December 2018, pp. 59-73
-
- Article
- Export citation
ON NONLOCAL NONLINEAR ELLIPTIC PROBLEMS WITH THE FRACTIONAL LAPLACIAN
- Part of:
-
- Published online by Cambridge University Press:
- 29 January 2019, pp. 75-84
-
- Article
- Export citation
AN ALGORITHM TO CONSTRUCT THE LE DIAGRAM ASSOCIATED TO A GRASSMANN NECKLACE
- Part of:
-
- Published online by Cambridge University Press:
- 18 January 2019, pp. 85-91
-
- Article
- Export citation
ON THE NUMBER OF REAL CLASSES IN THE FINITE PROJECTIVE LINEAR AND UNITARY GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 31 January 2019, pp. 93-107
-
- Article
- Export citation
A CLASS OF CRITICAL KIRCHHOFF PROBLEM ON THE HYPERBOLIC SPACE
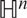 $\mathbb{H}^{{\it n}}$
$\mathbb{H}^{{\it n}}$
- Part of:
-
- Published online by Cambridge University Press:
- 21 January 2019, pp. 109-122
-
- Article
- Export citation
LOCAL NEGATIVITY OF SURFACES WITH NON-NEGATIVE KODAIRA DIMENSION AND TRANSVERSAL CONFIGURATIONS OF CURVES
- Part of:
-
- Published online by Cambridge University Press:
- 18 January 2019, pp. 123-135
-
- Article
- Export citation
CHARACTERIZATIONS OF BERGER SPHERES FROM THE VIEWPOINT OF SUBMANIFOLD THEORY
- Part of:
-
- Published online by Cambridge University Press:
- 01 March 2019, pp. 137-145
-
- Article
- Export citation
ORIENTED FLIP GRAPHS, NONCROSSING TREE PARTITIONS, AND REPRESENTATION THEORY OF TILING ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 07 February 2019, pp. 147-182
-
- Article
-
- You have access
- Export citation
CENTRALIZERS OF p-SUBGROUPS IN SIMPLE LOCALLY FINITE GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 21 February 2019, pp. 183-186
-
- Article
-
- You have access
- Open access
- Export citation
NONNEGATIVE MULTIPLICATIVE FUNCTIONS ON SIFTED SETS, AND THE SQUARE ROOTS OF −1 MODULO SHIFTED PRIMES
- Part of:
-
- Published online by Cambridge University Press:
- 20 February 2019, pp. 187-199
-
- Article
- Export citation
THE UNITAL EXT-GROUPS AND CLASSIFICATION OF C*-ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 13 March 2019, pp. 201-231
-
- Article
- Export citation
EPSILON-STRONGLY GROUPOID-GRADED RINGS, THE PICARD INVERSE CATEGORY AND COHOMOLOGY
- Part of:
-
- Published online by Cambridge University Press:
- 12 March 2019, pp. 233-259
-
- Article
-
- You have access
- Open access
- Export citation
Front Cover (OFC, IFC) and matter
GMJ volume 62 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 03 December 2019, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
GMJ volume 62 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 03 December 2019, pp. b1-b2
-
- Article
-
- You have access
- Export citation