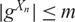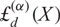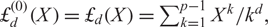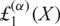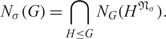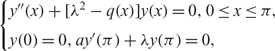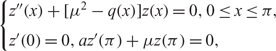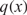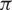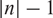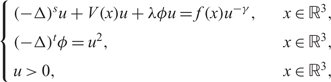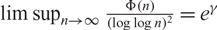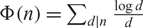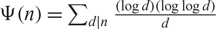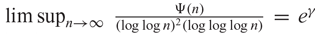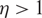Research Article
POWERS OF THE MAXIMAL IDEAL AND VANISHING OF (CO)HOMOLOGY
- Part of:
-
- Published online by Cambridge University Press:
- 10 January 2020, pp. 1-5
-
- Article
- Export citation
HOW A NONASSOCIATIVE ALGEBRA REFLECTS THE PROPERTIES OF A SKEW POLYNOMIAL
- Part of:
-
- Published online by Cambridge University Press:
- 26 November 2019, pp. 6-26
-
- Article
- Export citation
HOMOLOGY THEORIES FOR COMPLEXES BASED ON FLATS
- Part of:
-
- Published online by Cambridge University Press:
- 02 December 2019, pp. 27-44
-
- Article
- Export citation
THE GLOBAL CAUCHY PROBLEM FOR THE NLS WITH HIGHER ORDER ANISOTROPIC DISPERSION
- Part of:
-
- Published online by Cambridge University Press:
- 12 December 2019, pp. 45-53
-
- Article
-
- You have access
- Open access
- Export citation
ON FINITE-BY-NILPOTENT GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 20 December 2019, pp. 54-58
-
- Article
- Export citation
GAPS BETWEEN CONSECUTIVE UNTWISTING NUMBERS
- Part of:
-
- Published online by Cambridge University Press:
- 03 February 2020, pp. 59-65
-
- Article
- Export citation
GENERALIZED FINITE POLYLOGARITHMS
- Part of:
-
- Published online by Cambridge University Press:
- 19 February 2020, pp. 66-80
-
- Article
- Export citation
FINITENESS OF TOPOLOGICAL ENTROPY FOR LOCALLY COMPACT ABELIAN GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2020, pp. 81-105
-
- Article
- Export citation
WILD RAMIFICATION IN TRINOMIAL EXTENSIONS AND GALOIS GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 12 March 2020, pp. 106-120
-
- Article
- Export citation
ON THE σ-NILPOTENT NORM AND THE σ-NILPOTENT LENGTH OF A FINITE GROUP
- Part of:
-
- Published online by Cambridge University Press:
- 27 February 2020, pp. 121-132
-
- Article
- Export citation
A NOTE ON CHAINS AND BOUNDING PAIRS OF DEHN TWISTS
- Part of:
-
- Published online by Cambridge University Press:
- 15 May 2020, pp. 133-138
-
- Article
- Export citation
(WEAK) INCIDENCE BIALGEBRAS OF MONOIDAL CATEGORIES
- Part of:
-
- Published online by Cambridge University Press:
- 16 March 2020, pp. 139-157
-
- Article
-
- You have access
- Open access
- Export citation
ON THE EIGENVALUES AND THE NODAL POINTS OF THE EIGENFUNCTIONS OF SOME EIGENVALUE PROBLEMS WITH EIGENPARAMETER-DEPENDENT BOUNDARY CONDITIONS
- Part of:
-
- Published online by Cambridge University Press:
- 07 April 2020, pp. 158-178
-
- Article
- Export citation
FRACTIONAL SCHRÖDINGER–POISSON SYSTEM WITH SINGULARITY: EXISTENCE, UNIQUENESS, AND ASYMPTOTIC BEHAVIOR
- Part of:
-
- Published online by Cambridge University Press:
- 12 March 2020, pp. 179-192
-
- Article
- Export citation
AN EXTENSION OF A RESULT OF ERDŐS AND ZAREMBA
- Part of:
-
- Published online by Cambridge University Press:
- 13 May 2020, pp. 193-222
-
- Article
- Export citation
ON SOME QUESTIONS OF PARTITIO NUMERORUM: TRES CUBI
- Part of:
-
- Published online by Cambridge University Press:
- 21 April 2020, pp. 223-244
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
GMJ volume 63 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 15 December 2020, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
GMJ volume 63 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 15 December 2020, pp. b1-b2
-
- Article
-
- You have access
- Export citation