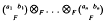Research Article
Complemented subspaces and the Hahn-Banach extension property in lp(0 < p < 1)
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 115-120
-
- Article
-
- You have access
- Export citation
A non-smooth extension of Frechet differentiability of the norm with applications to numerical ranges
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 121-137
-
- Article
-
- You have access
- Export citation
A Simple proof of the Goldberg–Straus theorem on numerical radii
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 139-141
-
- Article
-
- You have access
- Export citation
Products of idempotents in regular rings
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 143-152
-
- Article
-
- You have access
- Export citation
On normally embedded subgroups of locally soluble FC-groups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 153-159
-
- Article
-
- You have access
- Export citation
Free bands and free *-bands
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 161-179
-
- Article
-
- You have access
- Export citation
Clifford semigroups of left quotients
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 181-191
-
- Article
-
- You have access
- Export citation
Approximate point spectrum and commuting compact perturbations
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 193-198
-
- Article
-
- You have access
- Export citation
On generalized braid groups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 199-209
-
- Article
-
- You have access
- Export citation
Factorization and bounded approximate identities for a class of convolution Banach algebras
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 211-214
-
- Article
-
- You have access
- Export citation
Spectral operators and weakly compact homomorphisms in a class of Banach Spaces
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 215-222
-
- Article
-
- You have access
- Export citation
p-injectivity of simple pre-torsion modules
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 223-225
-
- Article
-
- You have access
- Export citation
Clifford division algebras and anisotropic quadratic forms: two counterexamples
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 227-228
-
- Article
-
- You have access
- Export citation
A theorem on polynomial lorentz structures
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 229-235
-
- Article
-
- You have access
- Export citation
A new characterization of Dedekind domains
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 237-239
-
- Article
-
- You have access
- Export citation
Corrigendum
Macbeath's Curve and the Modular Group
-
- Published online by Cambridge University Press:
- 18 May 2009, p. 241
-
- Article
-
- You have access
- Export citation
Front matter
GMJ volume 28 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
GMJ volume 28 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 18 May 2009, p. b1
-
- Article
-
- You have access
- Export citation

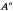 of a unital Banach algebra
of a unital Banach algebra 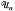 be its unitary group. Given
be its unitary group. Given 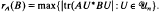
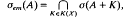
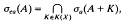
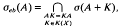
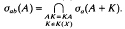
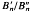 is free abelian of rank 2 if
is free abelian of rank 2 if 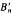 is finitely presented.
is finitely presented.