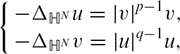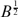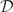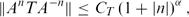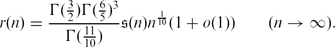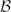Research Article
SOME REMARKS ON LANDAU–GINZBURG POTENTIALS FOR ODD-DIMENSIONAL QUADRICS
- Part of:
-
- Published online by Cambridge University Press:
- 18 December 2014, pp. 481-507
-
- Article
-
- You have access
- Export citation
FINITISTIC DIMENSIONS AND PIECEWISE HEREDITARY PROPERTY OF SKEW GROUP ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 18 December 2014, pp. 509-517
-
- Article
-
- You have access
- Export citation
SYMMETRY AND EXISTENCE OF SOLUTIONS OF SEMI-LINEAR ELLIPTIC SYSTEMS IN HYPERBOLIC SPACE
- Part of:
-
- Published online by Cambridge University Press:
- 18 December 2014, pp. 519-541
-
- Article
-
- You have access
- Export citation
ON THE COMPLEXITY OF FINDING A NECESSARY AND SUFFICIENT CONDITION FOR BLASCHKE-OSCILLATORY EQUATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 17 December 2014, pp. 543-554
-
- Article
-
- You have access
- Export citation
GK DIMENSION AND LOCALLY NILPOTENT SKEW DERIVATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 18 December 2014, pp. 555-567
-
- Article
-
- You have access
- Export citation
QUASI-EINSTEIN CONTACT METRIC MANIFOLDS
- Part of:
-
- Published online by Cambridge University Press:
- 18 December 2014, pp. 569-577
-
- Article
-
- You have access
- Export citation
REPRESENTATIONS OF ALTERNATIVE CLIFFORD ALGEBRAS OF QUADRATIC FORMS
- Part of:
-
- Published online by Cambridge University Press:
- 18 December 2014, pp. 579-590
-
- Article
-
- You have access
- Export citation
LINEAR AND PROJECTIVE BOUNDARY OF NILPOTENT GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 22 December 2014, pp. 591-632
-
- Article
-
- You have access
- Export citation
ON BI-HARMONIC HYPERSURFACES IN EUCLIDEAN SPACE OF ARBITRARY DIMENSION
- Part of:
-
- Published online by Cambridge University Press:
- 18 December 2014, pp. 633-642
-
- Article
-
- You have access
- Export citation
CHARACTERIZATIONS OF RICCI FLAT METRICS AND LAGRANGIAN SUBMANIFOLDS IN TERMS OF THE VARIATIONAL PROBLEM
- Part of:
-
- Published online by Cambridge University Press:
- 17 December 2014, pp. 643-651
-
- Article
-
- You have access
- Export citation
LINEAR WEINGARTEN HYPERSURFACES WITH BOUNDED MEAN CURVATURE IN THE HYPERBOLIC SPACE
- Part of:
-
- Published online by Cambridge University Press:
- 17 December 2014, pp. 653-663
-
- Article
-
- You have access
- Export citation
GROWTH CONDITIONS FOR OPERATORS WITH SMALLEST SPECTRUM
- Part of:
-
- Published online by Cambridge University Press:
- 18 December 2014, pp. 665-680
-
- Article
-
- You have access
- Export citation
ON THE ASYMPTOTIC FORMULA IN WARING'S PROBLEM: ONE SQUARE AND THREE FIFTH POWERS
- Part of:
-
- Published online by Cambridge University Press:
- 18 December 2014, pp. 681-692
-
- Article
-
- You have access
- Export citation
DIRECTLY FINITE ALGEBRAS OF PSEUDOFUNCTIONS ON LOCALLY COMPACT GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 17 December 2014, pp. 693-707
-
- Article
-
- You have access
- Export citation
MAPS PRESERVING THE LOCAL SPECTRUM OF PRODUCT OF OPERATORS
- Part of:
-
- Published online by Cambridge University Press:
- 17 December 2014, pp. 709-718
-
- Article
-
- You have access
- Export citation
Front Cover (OFC, IFC) and matter
GMJ volume 57 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 23 July 2015, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
GMJ volume 57 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 23 July 2015, pp. b1-b4
-
- Article
-
- You have access
- Export citation