No CrossRef data available.
Article contents
Toeplitz and Hankel operators on Bargmann spaces
Published online by Cambridge University Press: 18 May 2009
Extract
Let μ be the Gaussian measure in ℂn given by dμ(z)=(2π)−n exp(−|z|2/2)dV, where dV is the ordinary Lebesgue measure in ℂn. The Segal-Bargmann space H2(μ) is the space of all entire functions on ℂn that belong to L2(μ)-the usual space of Gaussian square-integrable functions. Let P be the orthogonal projection from L2(μ) onto H2(μ). For a measurable function ϕ on ℂn, the multiplication operator Mϕ on L2(μ) is defined by Mϕh =ϕh. The Toeplitz operator Tϕ is defined on H2(μ)by
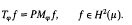
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1988


