Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Close cookie message
×
Home
  • Home
Hostname: page-component-559fc8cf4f-z4vvc Total loading time: 0.533 Render date: 2021-03-06T08:30:19.505Z Has data issue: true Feature Flags: { "shouldUseShareProductTool": true, "shouldUseHypothesis": true, "isUnsiloEnabled": true, "metricsAbstractViews": false, "figures": false, "newCiteModal": false, "newCitedByModal": true }
EnglishFrançais
Glasgow Mathematical Journal Glasgow Mathematical Journal

Article contents

SINGULAR LIMITS FOR 2-DIMENSIONAL ELLIPTIC PROBLEMS INVOLVING EXPONENTIAL NONLINEARITIES WITH SUB-QUADRATIC CONVECTION TERM

Published online by Cambridge University Press:  25 February 2013

SAMI BARAKET  and
TAIEB OUNI
SAMI BARAKET
Affiliation:
Department of Mathematics, College of Science King Saud University, P.O. Box 2455, Riyadh 11451, Saudi Arabia e-mail: sbaraket@ksu.edu.sa
TAIEB OUNI
Affiliation:
Département de Mathématiques, Faculté des Sciences de TunisCampus Universitaire, 2092 Tunis, Tunisia e-mail: Taieb.Ouni@fst.rnu.tn
Corresponding
E-mail address:
sbaraket@ksu.edu.sa
Taieb.Ouni@fst.rnu.tn
Save pdf (0.17 mb)
Rights & Permissions[Opens in a new window]

Abstract

Let Ω be a bounded domain with smooth boundary in ℝ2, q∈[1,2) and x1, x2,. . .,xm ∈ Ω. In this paper we are concerned with the following type of problem:

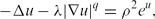\[ -\Delta u-\lambda|\nabla u|^q = \rho^{2}e^{u}, \]
with u = 0 on ∂ Ω. We use some nonlinear domain decomposition method to construct a positive weak solution vρ,λ in Ω, which tends to a singular function at each xi as the parameters ρ and λ tend to 0 independently.

Keywords

35J60 53C21 58J05
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 55 , Issue 3 , September 2013 , pp. 537 - 557
Copyright
Copyright © Glasgow Mathematical Journal Trust 2013 

References

1.Bandle, C. and Giarrusso, E., Boundary blowup for semilinear elliptic equations with nonlinear gradient terms, Adv. Differ. Equ. 1 (1996), 133–150.Google Scholar
2.Baraket, S., Ben Omrane, I. and Ouni, T., Singular limits for 2-dimensional elliptic problem involving exponential with nonlinear gradient term. Nonlinear Differ. Equ. Appl. 18 (2011), 59–78.CrossRefGoogle Scholar
3.Baraket, S., Ben Omrane, I., Ouni, T. and Trabelsi, N., Singular limits for 2-dimensional elliptic problem with exponentially dominated nonlinearity and singular data. Commun. Contemp. Math. 13 (4) (2011), 1–29.CrossRefGoogle Scholar
4.Baraket, S. and Pacard, F., Construction of singular limits for a semilinear elliptic equation in dimension 2, Calc. Var. Partial Differ. Equ. 6 (1998), 1–38.CrossRefGoogle Scholar
5.Del Pino, M., Kowalczyk, M. and Musso, M., Singular limits in Liouville type equations, Calc. Var. Partial Differ. Equ. 24 (2005), 47–81.CrossRefGoogle Scholar
6.Esposito, P., Grossi, M. and Pistoia, A., On the existence of blowing-up solutions for a mean field equation, Ann. I. H. Poincaré 22 (2005), 227–257.CrossRefGoogle Scholar
7.Esposito, P., Musso, M. and Pistoia, A., Concentrating solutions for a planar problem involving nonlinearities with large exponent, J. Differ. Equ. 227 (2006), 29–68.CrossRefGoogle Scholar
8.Ghergu, M. and Radulescu, V., On the influence of a subquadratic term in singular elliptic problems, in Applied analysis and differential equations (Carja, O. and Vrabie, I., Editors) (World Scientific, Singapore, 2007), 127–138.CrossRefGoogle Scholar
9.Giarrusso, E., Asymptotic behavior of large solutions of an elliptic quasilinear equation with a borderline case, C. R. Acad. Sci. Paris, Ser. I. 331 (2000), 777–782.CrossRefGoogle Scholar
10.Giarrusso, E., On blow up solutions of a quasilinear elliptic equation, Math. Nachr. 213 (2000), 89–104.3.0.CO;2-1>CrossRefGoogle Scholar
11.Greco, A. and Porru, G., Asymptotic estimates and convexity of large solutions to semilinear elliptic equations, Differ. Integral Equ. 10 (1997), 219–229.Google Scholar
12.Kristëly, A., Radulescu, V. and Varga, C., Variational principles in mathematical physics, geometry, and economics: Qualitative analysis of nonlinear equations and unilateral problems, encyclopedia of mathematics and its applications, vol. 136 (Cambridge University Press, Cambridge, UK, 2010).CrossRefGoogle Scholar
13.Liouville, J., Sur l'équation aux différences partielles $\partial^{2}\log\frac{\lambda}{\partial u \partial v}\pm\frac{\lambda}{2a^{2}} = 0 $, J. Math. 18 (1853), 17–72.Google Scholar
14.Marcus, M. and Véron, L., Uniqueness of solutions with blowup on the boundary for a class of nonlinear elliptic equations, C. R. Acad. Sci. Paris, Ser. I. 317 (1993), 557–563.Google Scholar
15.Osserman, R., On the inequality Δu ≥ f(u), Pacific J. Math. 7 (1957), 1641–1647.CrossRefGoogle Scholar
16.Rébai, Y., Weak solutions of nonlinear elliptic with prescribed singular set, J. Differ. Equ. 127 (2) (1996), 439–453.CrossRefGoogle Scholar
17.Ren, X. and Wei, J., On a two-dimensional elliptic problem with large exponent in nonlinearity, Trans. Am. Math. Soc. 343 (1994), 749–763.CrossRefGoogle Scholar
18.Suzuki, T., Two dimensional Emden–Fowler equation with exponential nonlinearity, in Nonlinear diffusion equations and their equilibrium states 3 (Birkäuser, Berlin, Germany, 1992), 493–512.CrossRefGoogle Scholar
19.Tao, S. and Zhang, Z., On the existence of explosive solutions for semilinear elliptic problems, Nonlinear Anal. 48 (2002), 1043–1050.CrossRefGoogle Scholar
20.Tarantello, G., On Chern-Simons theory, in Nonlinear PDE's and physical modeling: Superfluidity, superconductivity and reactive flows (Berestycki, H. editor) (Kluver, Dordrecht, Netherlands, 2002), 507–526.Google Scholar
21.Wei, J., Ye, D. and Zhou, F., Bubbling solutions for an anisotropic Emden-Fowler equation, Calc. Var. Partial Differ. Equ. 28 (2) (2007), 217–247.CrossRefGoogle Scholar
22.Weston, V. H., On the asymptotique solution of a partial differential equation with exponential nonlinearity, SIAM J. Math. 9 (1978), 1030–1053.CrossRefGoogle Scholar
23.Wong, J. S. W., On the generalized Emden-Fowler equation, SIAM Rev. 17 (1975), 339–360.CrossRefGoogle Scholar
24.Zhang, Z. and Tao, S., On the existence and asymptotic behaviour of explosive solutions for semilinear elliptic problems, Acta Math. Sin. 45A (2002), 493–700 (in Chinese).Google Scholar
25.Zhao, C., Blowing-up solutions to an anistropic Emden-Fowler equation with a singular source, J. Math. Anal. Appl. 342 (2008), 398–422.CrossRefGoogle Scholar

Full text views

Full text views reflects PDF downloads, PDFs sent to Google Drive, Dropbox and Kindle and HTML full text views.

Total number of HTML views: 0
Total number of PDF views: 62 *
View data table for this chart

* Views captured on Cambridge Core between September 2016 - 6th March 2021. This data will be updated every 24 hours.

Access
1 Cited by

Send article to Kindle

To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about sending to your Kindle.

Note you can select to send to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be sent to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

SINGULAR LIMITS FOR 2-DIMENSIONAL ELLIPTIC PROBLEMS INVOLVING EXPONENTIAL NONLINEARITIES WITH SUB-QUADRATIC CONVECTION TERM
Available formats
×

Send article to Dropbox

To send this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Dropbox.

SINGULAR LIMITS FOR 2-DIMENSIONAL ELLIPTIC PROBLEMS INVOLVING EXPONENTIAL NONLINEARITIES WITH SUB-QUADRATIC CONVECTION TERM
Available formats
×

Send article to Google Drive

To send this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Google Drive.

SINGULAR LIMITS FOR 2-DIMENSIONAL ELLIPTIC PROBLEMS INVOLVING EXPONENTIAL NONLINEARITIES WITH SUB-QUADRATIC CONVECTION TERM
Available formats
×
×

Reply to: Submit a response

Your details

Conflicting interests

Do you have any conflicting interests? *