Hostname: page-component-848d4c4894-x24gv Total loading time: 0 Render date: 2024-05-21T04:09:13.745Z Has data issue: false hasContentIssue false
  • English
  • Français

On the derivatives at the origin of entire harmonic functions

Published online by Cambridge University Press:  18 May 2009

D. H. Armitage
D. H. Armitage
Affiliation:
The Queen's University, Belfast BT7 1NN.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If f is an entire function in the complex plane such that

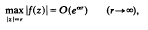
where 0 ≤ α < 1, and all the derivatives of f at 0 are integers, then it is easy to show that f is a polynomial (see e.g. Straus [10]). The best possible result of this type was proved by Pólya [9]. The main aim of this paper is to prove two analogous results for harmonic functions defined in the whole of the Euclidean space Rn, where n ≥ 2 (i.e. entire harmonic functions).

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 20 , Issue 2 , July 1979 , pp. 147 - 154
Copyright
Copyright © Glasgow Mathematical Journal Trust 1979

References

REFERENCES

1.Armitage, D. H., Uniqueness theorems for harmonic functions which vanish at lattice points, J. Approximation Theory (to appear).Google Scholar
2.Brelot, M. and Choquet, G., Polynômes harmoniques et polyharmoniques, Deuxième colloque sur les équations aux derivées partielles, Bruxelles (1954), 45–66.Google Scholar
3.Calderón, A. P. and Zygmund, A., On higher gradients of harmonic functions, Studia Math. 24 (1964), 211–226.CrossRefGoogle Scholar
4.Hayman, W. K., Power series expansions for harmonic functions, Bull. London Math. Soc. 2 (1970), 152–158.CrossRefGoogle Scholar
5.Helms, L. L., Introduction to potential theory (New York, 1969).Google Scholar
6.Kuran, Ü., On norms of higher gradients of harmonic functions, J. London Math. Soc. (2) 3 (1971), 761–766.CrossRefGoogle Scholar
7.Kuran, Ü., On Brelot-Choquet axial polynomials, ibid. (2) 4 (1971), 15–26.Google Scholar
8.Müller, C., Spherical harmonics, Lecture Notes in Mathematics, No. 17, (Springer-Verlag, 1966).CrossRefGoogle Scholar
9.Pólya, G., Über die kleinsten ganzen Funktionen, deren sämtliche Derivierten im Punkte z=0 ganzzahlig sind, Tôhoku Math. J. 19 (1921), 65–68.Google Scholar
10.Straus, E. G., On entire functions with algebraic derivatives at certain algebraic points, Ann. of Math. 52 (1950), 188–198.CrossRefGoogle Scholar