Hostname: page-component-76fb5796d-zzh7m Total loading time: 0 Render date: 2024-04-28T17:51:56.782Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on the joint operator norm of hermitian operators on Banach spaces

Published online by Cambridge University Press:  18 May 2009

Muneo Chō  and
Tadasi Huruya
Muneo Chō
Affiliation:
Department of Mathematics, Joetsu University of Education, Joetsu 943, Japan
Tadasi Huruya
Affiliation:
Faculty of Education, Niigata University, Niigata 950-21, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X be a complex Banach space and H be a hermitian operator on X. Then in [7] Sinclair proved that r(H) = ¶H¶, where r(H) and ¶H¶ are the spectral radius and the operator norm of H, respectively.

For a commuting n-tuple T = (T1,…, Tn) of operators on X, we denote the (Taylor) joint spectrum of T by σ(T) (see [9]) and define the joint operator norm ¶T¶ and the joint spectral radius r(T) by

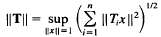
and

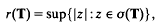
respectively.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 34 , Issue 2 , May 1992 , pp. 219 - 220
Copyright
Copyright © Glasgow Mathematical Journal Trust 1992

References

REFERENCES

1.Bonsall, F. F. and Duncan, J., Numerical ranges II (Cambridge Univ. Press, 1973).CrossRefGoogle Scholar
2.Chō, M., Joint spectra of commuting normal operators on Banach spaces, Glasgow Math. J. 30 (1988), 339–345.CrossRefGoogle Scholar
3.Chō, M. and Takaguchi, M., Some classes of commuting n-tuple of operators, Studia Math. 80 (1984), 245–259.CrossRefGoogle Scholar
4.Chō, M. and Yamaguchi, H., A simple example of a normal operator Tsuch that r(T)<¶T¶, Proc. Amer. Math. Soc. 108 (1990), 143.CrossRefGoogle Scholar
5.Rosenblum, M., On the operator equation BX – XB =Q, Duke Math. J. 23 (1956), 263–269.CrossRefGoogle Scholar
6.Shaw, S.-Y., On numerical ranges of generalized derivations and related properties, J. Australian Math. Soc.(A) 36 (1984), 134–142.CrossRefGoogle Scholar
7.Sinclair, A. M., The norm of a hermitian element in a Banach algebra, Proc. Amer. Math. Soc. 28 (1971), 446–450.CrossRefGoogle Scholar
8.Stampfli, J. G., The norm of a derivation, Pacific J. Math. 33 (1970), 737–747.CrossRefGoogle Scholar
9.Taylor, J. L., A joint spectrum for several commuting operators, J. Functional Anal. 6 (1970), 172–191.CrossRefGoogle Scholar