Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Robati, B. Khani
2007.
ON THE COMMUTANT OF MULTIPLICATION OPERATORS WITH ANALYTIC POLYNOMIAL SYMBOLS.
Bulletin of the Korean Mathematical Society,
Vol. 44,
Issue. 4,
p.
683.
Tikaradze, Akaki
2012.
Centralizers of Toeplitz Operators with Polynomial Symbols.
Complex Analysis and Operator Theory,
Vol. 6,
Issue. 6,
p.
1275.


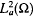 is defined to be the set of all analytic functions from ω into ℂ such that
is defined to be the set of all analytic functions from ω into ℂ such that