1. Introduction
Bayesian shrinkage mapping refers to a quantitative trait locus (QTL) mapping procedure that estimates QTL effects for all marker intervals simultaneously in a single model without performing variable selection. The method works through shrinking the estimated effects of QTL misplaced in marker intervals that contain no QTLs. When all markers are included in a single model, the method is called genome selection (Meuwissen et al., Reference Meuwissen, Hayes and Goddard2001). The original idea of genome selection of Meuwissen et al. (Reference Meuwissen, Hayes and Goddard2001) was developed for random populations. Xu (Reference Xu2003) extended genome selection to handle data for line crosses. Wang et al. (Reference Wang, Zhang, Li, Masinde, Mohan, Baylink and Xu2005) further extended the method to handle a single binary or ordinal trait and allow QTL positions to be searched uniformly within marker intervals. Wang et al. (Reference Wang, Zhang, Li, Masinde, Mohan, Baylink and Xu2005) showed that the shrinkage method outperformed the multiple interval mapping (MIM) procedure of Kao et al. (Reference Kao, Zeng and Teasdale1999).
The theoretical basis of shrinkage mapping and the derivation of the shrinkage estimates were given by Xu (Reference Xu2007a). The basic idea was to treat each QTL effect as a random variable so that the variance of the QTL effect can be estimated from the data. This variance is then used as a shrinkage factor to shrink small effect QTLs to zero. The shrinkage method has been applied to mapping QTLs responsible for variation of sexually dimorphic traits in Drosophila melanogaster (Kopp et al., Reference Kopp, Graze, Xu, Carroll and Nuzhdin2003). Recently, Xu & Jia (Reference Xu and Jia2007) analysed seven quantitative traits of barley for epistatic effects using the shrinkage method. They detected many main effect QTLs and some QTLs with epistatic effects. Huang et al. (Reference Huang, Eversley, Threadgill and Zou2007) extended the shrinkage method to map QTLs for binary traits. They identified several QTLs controlling the variation of colorectal tumour development in mice.
The method is so simple to implement and yet it is so powerful that a QTL even explaining as small as 1% of the phenotypic variance can be detected (Wang et al., Reference Wang, Zhang, Li, Masinde, Mohan, Baylink and Xu2005; Huang et al., Reference Huang, Eversley, Threadgill and Zou2007; Xu, Reference Xu2007b; Xu & Jia, Reference Xu and Jia2007). The method appears to have pointed to a new direction for mapping multiple QTLs. Shrinkage mapping for a single quantitative trait has been fully developed. It is natural to extend the method to map QTLs for multiple traits. So far there has been no report of such an extension. Banerjee et al. (Reference Banerjee, Yandell and Yi2008) recently published a Bayesian multivariate mapping procedure. They used the stochastic search variable selection (SSVS) approach (Yi, Reference Yi2004), also called the composite model space approach, to search for the locations of QTLs. This algorithm introduces additional binary variables to indicate the states of inclusion and exclusion of a locus, which is different from the Bayesian shrinkage method. In addition, the Bayesian method of Banerjee et al. (Reference Banerjee, Yandell and Yi2008) has not addressed the situation where a trait set contains both continuous and categorical traits. Yang & Xu (Reference Xu2007) recently explored the possibility of extending the shrinkage method to map QTLs for dynamic traits, traits that are measured repeatedly over time. Even though dynamic traits can be treated as multivariate traits, there are some important differences between the models. The emphasis of dynamic trait mapping is on modelling the covariance matrix structure of the residual errors, whereas the multiple trait QTL mapping proposed here uses a fully unstructured residual covariance matrix.
The proposed Bayesian mapping for multiple traits also differ from the dynamic trait QTL mapping in that we can handle a multiple trait set that contains binary trait components. In fact, many traits in agricultural species are measured in binary or ordered category. For example, disease resistance traits are commonly measured as presence or absence of disease symptoms. These traits are not continuously distributed and thus additional steps are required to link the normal theory to categorical trait mapping. Once categorical traits are involved in the multiple trait set, the maximum likelihood method becomes less powerful, because the model will be so complicated that it is beyond the capability of Maximum Likelihood (ML) analysis. Therefore, Bayesian inference is one of a few choices for modelling multiple traits with mixed types of trait components. Korsgaard et al. (Reference Korsgaard, Lund, Sorensen, Gianola, Madsen and Jensen2003) developed the multivariate Bayesian inference for a trait set that contains both continuous and categorical traits. However, the method is not for QTL mapping but for classical quantitative trait analysis, aiming to estimating heritability and genetic correlation. Xu et al. (Reference Xu, Li and Xu2005) developed an ML method for mapping multiple trait sets with binary trait components, but this method can only handle two traits without involving Monte Carlo sampling. With more than two traits, Monte Carlo sampling is required to generate the liabilities of binary traits. In addition, the method of Xu et al. (Reference Xu, Li and Xu2005) is an interval mapping approach where only a single QTL is included in a model.
The primary goal of the present work is to develop a multivariate version of the Bayesian shrinkage methodology for joint mapping of QTLs underlying multiple traits. The second objective is to construct a unified Bayesian method that is capable of handling joint mapping of a multiple trait set with binary trait components but treating the conventional multiple continuous traits joint mapping (Jiang & Zeng, Reference Jiang and Zeng1995) and multiple dichotomous traits joint mapping (Xu et al., Reference Xu, Li and Xu2005) as special cases. We applied the method to both simulated and real data set. Results of the real data analysis can be directly interpreted by interested biologists and made available to plant geneticists and breeders for further investigation.
2. Methods
(i) Multivariable linear model
Let y j=[y 1j … y qj]T, for j=1, …, n, be a q×1 vector for the phenotypic values of q quantitative traits measured from the jth individual of an F2 mapping population, where n is the sample size. The vector of phenotypic values is described by the following multivariate linear model:
where μ=[μ1 … μq]T is an q×1 vector of population means (or intercepts) for the q traits, αk=[α1k … αqk]T and βk=[β1k … βqk]T are the additive and dominance effects, respectively, for locus k (k=1, …,p) and p is the number of loci included in the model. Both αk and βk are q×1 vectors because there are q traits involved in the model. The residual error e j=[e 1j … e qj]T is a q×1 vector with an assumed multivariate normal distribution N(0, Σ), where Σ is a q×q positive definite variance–covariance matrix. The independent variables, x jk and zjk, are defined as follows. Let A 1A 1, A 1A 2 and A 2A 2 be the three genotypes at locus k. These two variables are

The scales of these independent variables are arbitrary. Alternative scales have been used by other investigators, e.g. Yang et al. (Reference Yang, Tian and Xu2006).
(ii) Likelihood function
Under the assumption of normal distribution for the residual errors, the conditional probability density of y j is

Given x j, the phenotypes and the markers are independent. Therefore, the joint distribution of the data {y j, m j} is
where m j represents the marker variables and p(m j | x j, λ) is the joint distribution of marker genotypes given the genotype of QTLs and the location of the QTLs relative to the locations of markers (Jiang & Zeng, Reference Jiang and Zeng1997). The likelihood function of the parameters is proportional to
where m={m j}jn and y={y j}jn are collectively called the data, denoted by d={m, y}, and θ={λ, μ, α, β, Σ} are the parameters. The QTL genotype array, x={x j}j=1n, are not parameters of interest but missing values in QTL mapping. They are interesting quantities when marker-assisted selection is considered after QTL mapping. The likelihood function serves as a link between the data, the parameters and the missing values. Combined with the prior distribution of the parameters, the likelihood function is used to derive the posterior distribution of the parameters. The number of QTLs is p, which is supposed to be a parameter of interest in the classical QTL mapping experiment, but in the Bayesian shrinkage analysis, it is a preset constant. We set p as the number of marker intervals. If an interval does not contain a QTL, the QTL effects will be shrunk to zero. Therefore, a QTL with effect of zero is equivalent to being excluded from the model. With this shrinkage analysis, model selection is not conducted explicitly but implicitly via shrinkage.
(iii) Prior distribution
Each of the parameters is assigned a prior distribution. The population mean μ can be estimated accurately from the data, and thus a flat prior is given to μ, i.e. p(μ)=constant. Each of the QTL effect vectors is assigned a normal prior, p(αk)=N(αk | 0, A k) and p(βk)=N(βk | 0, B k), where A k and B k are unknown variance–covariance matrices with dimension q×q. The above notation for the probability distribution is adopted from Gelman et al. (2004), which are equivalently expressed as αk~N(0, A k) and βk~N(0, B k). The key difference between the shrinkage analysis and the usually Bayesian regression analysis is that these prior variance–covariance matrices are effect-specific, i.e. they vary across different loci. Another difference between the two is that the hyper-parameters (parameters of the prior), A k and B k, are not known a priori but estimated from the data. To do this, we give each of them a prior distribution. Once we assign a prior distribution to a hyper-parameter, there will be multilevel prior assignment. This is called hierarchical modelling (Lindley & Smith, Reference Lindley and Smith1972). We assign the variance–covariance matrices with the following inverse Wishart distributions: p(A k)=Inv-Wishart(A k | τ, Г) and p(B k)=Inv-Wishart(B k | τ, Г), where τ>q and Г>0 are the prior degree of freedom and prior scale matrix. These hyper-parameters are already remote from αk and βk, and thus they can be preset with some convenient values (constant across loci) without affecting the posterior inference of the QTL effects. To reflect the lack of knowledge, τ and Г are set with values as small as possible, e.g. τ=q+1 and Г=0.1×I q, where I q is a q×q identity matrix. The residual variance–covariance matrix is also assigned the same inverse Wishart distribution, p(Σ)=Inv-Wishart(Σ|τ, Г). Although Σ is a parameter of interest, data are usually sufficient to provide an accurate estimate of Σ, and thus the hyper-parameters τ and Г will have little influence on the estimated Σ. Finally, a uniform prior distribution for λk is chosen. Since we assume that each marker interval contains one and only one QTL, the uniform distribution for λk is p(λk)=U(λk | ξkL, ξkR)=1/(ξkR–ξkL). All these priors are independent across loci. Therefore, the joint prior distribution of the parameters is
The distribution of QTL genotype array is
(iv) Posterior distribution
The joint distribution of the data, the parameters (including the hyper-parameters) and the missing values (QTL genotype array) is
The posterior distribution of {θ, x} is
Although, in Bayesian analysis, we are interested in the posterior distribution of the parameters, ![]() , this distribution is hard to derive. Therefore, we use the MCMC sampling to draw samples from the distribution given by p(θ, x|d). The MCMC samples will provide an empirical distribution of p(θ, x|d), from which p(θ|d) can be inferred.
, this distribution is hard to derive. Therefore, we use the MCMC sampling to draw samples from the distribution given by p(θ, x|d). The MCMC samples will provide an empirical distribution of p(θ, x|d), from which p(θ|d) can be inferred.
To simplify the sampling process, it is easier to sample one variable at a time conditional on values of all other variables. The single variable defined here means a vector of variables with the same type. For example, αk is defined as a variable, but it is a vector containing the additive effects for all traits. The conditional posterior distribution for one variable usually has an explicit form of the distribution, making Monte Carlo simulation easy. We now provide the posterior distribution for each of the parameters.
The conditional posterior distribution of μ is multivariate normal with mean and variance given by
and
respectively, where the special notation (μ| …) means conditional on all other variables.
The conditional posterior for αk is multivariate normal with the following mean and variance:

and

Similarly, the conditional posterior for βk is also multivariate normal with mean and variance of

and

respectively. The conditional posterior means of αk and βk are called the shrinkage estimates. Derivation of the shrinkage estimates can be found in a recent paper by Xu (Reference Xu2007a).
The hierarchical model also requires sampling of A k and B k from their conditional posterior distribution. The inverse Wishart prior is conjugate and thus the conditional posteriors of A k and B k are also inverse Wishart,
and
The conditional posterior for the residual variance–covariance matrix is inverse Wishart due to the conjugate nature of the prior,
where

The distribution of x jk is discrete, and thus the conditional posterior distribution can be obtained from Bayes' theorem. Let
be the three genotype indicators for the variable x jk and
be the three genotype indicators for the variable z jk. Assume that m jkL=g u (u=1, 2, 3) and m jkR=g v (v=1, 2, 3) are the observed genotypes for the two flanking markers. The conditional posterior probability for x jk=g w (w=1, 2, 3) is calculated using the following Bayes' theorem:
where
is the Mendelian segregation ratio. Other items in the above Bayes' theorem are defined as follows:
is the adjusted phenotypic value of individual j by removing effects of all other QTLs except k. The variable ![]() is the transition matrix between QTL k and marker m L. The variable
is the transition matrix between QTL k and marker m L. The variable ![]() is the transition matrix between QTL k and marker m R.
is the transition matrix between QTL k and marker m R.
The conditional posterior distribution of the position of QTL k, p(λk | …), has no explicit form due to the complexity of the model. Therefore, λk must be sampled from a Metropolis–Hastings (Metropolis et al., Reference Metropolis, Rosenbluth, Rosenbluth, Teller and Teller1953; Hastings, Reference Hastings1970) algorithm. The algorithm presented by Wang et al. (Reference Wang, Zhang, Li, Masinde, Mohan, Baylink and Xu2005) for univariate QTL mapping can be directly adopted here for multivariate QTL mapping.
Finally, when a marker genotype is missing, it must be sampled from its conditional posterior distribution, which is calculated from the following Bayes' theorem:

where the marker is located between QTL k−1 and k. The prior probability of marker genotype, p(m=g w), takes the Mendelian segregation ratio, i.e.
H m(k−1) and H mk are the transition matrices between the marker and the two flanking QTLs, assuming that the QTL on the left has a genotype of g u and the QTL on the right has a genotype of g v.
If a marker is located in one end of a chromosome, the conditional probabilities can only be calculated based on one QTL that is proximate to the marker. In this case, the conditional posterior probability is
where the QTL proximate to the marker is denoted by locus k, where k=1 means that the marker is located in the left end and k=p means that the marker is in the other end of the chromosome.
(v) MCMC sampling
The MCMC sampling process is summarized as follows:
(1) Initialize all variables, including parameters and missing values, with some values in their legal domains.
(2) Sample μ from its conditional posterior distribution (multivariate normal).
(3) Sample αk and βk from their conditional posterior distributions (multivariate normal).
(4) Sample A k and B k from their conditional posterior distributions (inverse Wishart).
(5) Sample Σ from its conditional posterior distribution (inverse Wishart).
(6) Sample QTL genotypes from their conditional posterior distributions (derived from Bayes' theorem).
(7) Sample genotypes of missing markers from their conditional posterior distributions (derived from Bayes' theorem).
(8) Sample QTL positions from their conditional posterior distribution using the Metropolis–Hastings algorithm.
(9) Repeat steps (2)–(8) until the Markov chain is sufficiently long. Steps (2)–(7) are called the Gibbs sampler steps, while step (8) is called the M–H step.
How long is sufficiently long for the Markov chain? We used the algorithm of Gelman et al. (2004) to check the convergence of the chain. Once the chain is converged, one sampled observation of all variables is saved for every 50 iterations, producing a sufficiently large posterior sample for presentation.
(vi) Post-MCMC analysis
The product of MCMC sampling is a realized sample of all unknown variables from the joint posterior distribution. The MCMC does not result in a significance test but serves as a process of creating the empirical posterior distributions of parameters, from which all the information about the QTL is inferred. The most important parameters are the locations and the effects of the QTL, while the covariance matrices are not of immediate interest but assist in the estimation of the effects. In the conventional Bayesian mapping analysis (Sillanpaa & Arjas, 1998; Xu, Reference Xu, Camp and Cox2002), the marginal posterior distribution of QTL position was graphically summarized by plotting the number of hits by a QTL in a short region against the location where that short region occurs in the genome. The curve produced is called the QTL intensity profile. In the present study, we assume that each marker interval is associated with a QTL, and thus all intervals are hit by a QTL the same number of times. If an interval contains a real QTL, the QTL intensity profile within the interval is expected to show a peak. Otherwise, the intensity profile will be flat (uniform). Such a QTL intensity profile is denoted by f(λ), where λ now denotes a particular location of the genome.
The QTL intensity profile itself is not the best indicator of the QTL location under the Bayesian shrinkage analysis. We propose to weigh the intensity profile by the QTL effects and use the weighted QTL intensity profile to indicate the locations of the QTL. The majority of the genome segments have negligible QTL effects and thus only the areas with nontrivial QTL effects will show clear peaks. Let α(λ) and β(λ) be q×1 vectors of additive and dominance effects, respectively, of QTL collected at position λ of the genome. There are many ways to present the QTL effects as functions of genome location. However, we choose the following profile to present the QTL effects:
The coefficients ![]() and
and ![]() in front of the quadratic terms are the expected variances of x jk and z jk across individuals within the F2 population (assuming no segregation distortion). This QTL effect profile g(λ) reduces to
in front of the quadratic terms are the expected variances of x jk and z jk across individuals within the F2 population (assuming no segregation distortion). This QTL effect profile g(λ) reduces to ![]() in the special case of single trait analysis, which is the QTL variance at location λ. If desired, one can also draw the QTL effect profile for each trait or each effect of the trait (additive or dominance). The QTL effect profile presented here is the overall effect on the entire genome.
in the special case of single trait analysis, which is the QTL variance at location λ. If desired, one can also draw the QTL effect profile for each trait or each effect of the trait (additive or dominance). The QTL effect profile presented here is the overall effect on the entire genome.
The weighted QTL intensity profile is defined as
The intensity profile f(λ) does not tell much about QTL across marker intervals because each interval is hit by the same number of QTLs, but if an interval contains a QTL, f(λ) is able to show a peak within that interval. The QTL effect profile g(λ), on the other hand, can pick up the intervals with large effect QTL, but it is not sensitive to the change of location within an interval. Therefore, the weighted intensity profile w(λ) can pick up the intervals with QTL and also show sharp peaks within intervals.
In practice, not all traits are measured in the same scale. The profile of the overall QTL effect may be dominated by the traits with large variances. Two approaches may be taken to eliminate this problem. One is to standardize all traits before the analysis so that they all have roughly the same variance. Alternatively, g(λ) may be modified by
where Σ is the residual covariance matrix.
Pleiotropic effects can be visualized by comparing the weighted QTL intensity profiles for individual traits. Let α(λ)=[α1(λ) … αq(λ)]T be the additive effects of QTL at location λ, where αi(λ) is the effect for the ith trait for (i=1, …, q). Pleiotropic effect occurs at position λ if more than one component of α(λ) is noticeably large.
(vii) Extension to binary traits
With little effort, the method can be extended to handle binary traits. A binary trait is a categorical trait with two states: presence and absence. Recall that y j=[y 1j … y qj]T is a vector of phenotypic values for q quantitative traits. If the ith trait is binary, the phenotype is denoted by w ij={0, 1} with 0 representing absence and 1 representing presence. Under the threshold model for a binary trait (Xu et al., Reference Xu, Li and Xu2005), we propose that trait i is still a quantitative trait, but we cannot observe y ij. This latent quantitative trait, however, determines the observed binary phenotype. We propose a hypothetical threshold t i=0 so that w ij=0 for y ij⩽t i and w ij=1 for y ij>t i. The latent variable is still described by the usual linear model with normal residual error except that the residual error variance is set to 1 because it is not estimable. Under this threshold model, we can derive the conditional posterior distribution of y ij given w ij, the phenotypic values of all other traits and the current parameter values. This conditional posterior distribution happens to be a truncated normal distribution, from which y ij is sampled. Detailed algorithm for sampling y ij has been given by Xu et al. (Reference Xu, Li and Xu2005). Korsgaard et al. (Reference Korsgaard, Lund, Sorensen, Gianola, Madsen and Jensen2003) provided a general method for sampling the liability for ordered categorical traits. Again, their method is not for QTL mapping but for classical quantitative trait analysis. Once y ij is sampled, y j becomes a full vector of quantitative trait values. The MCMC sampling schemes described earlier applies. Therefore, mapping multiple traits with one or more binary trait components requires only one more step of sampling the missing phenotype of an underlying quantitative trait.
3. Results
(i) Simulated data
To investigate the applicability of the proposed method, two simulation experiments were conducted. In the first experiment, a single chromosome of length 100 cM with 11 evenly spaced markers was simulated. The experimental population was an F2 containing 500 individuals. Three pleiotropic QTLs with different levels of heritability (the proportions of variance explained by the simulated QTL) were simulated on the chromosome to jointly control the expression of three different traits. The detailed settings of their locations, the genetic effects and heritability are given in Table 1. The overall mean vector and the residual covariance matrix were set at
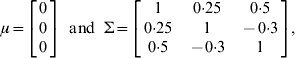
respectively. In order to demonstrate the joint mapping procedure for different combinations of phenotypes, we analysed three data sets: multiple quantitative traits, multiple binary traits and multiple traits with some binary components. Data one was simulated for three quantitative traits. Data two was generated by truncating each continuous phenotype in the first data set into a binary phenotype using a threshold value of t i=0 for i=1, 2, 3. Data three contains one ordinal trait and two continuous traits, which was obtained through truncating only the third liability into an ordinal of three categories using truncation points of t 1=0 and t 2=1·0 but left the first two traits intact. Note that for three categories, there are two truncation points. The hyper-parameter values in the inverse Wishart distribution were chosen as τ=q+1 and Г=I q.
Table 1. Locations and effects of simulated QTL in the first simulation experiment

The second simulation experiment was designed to evaluate the performance of the proposed method in the scenario when the number of model effects is very large. In this experiment, we simulated a genome of 1500 cM with 151 markers for an F2 population of 500 individuals. For convenience of programming, we arranged all markers in a single large chromosome with a 10 cM distance between consecutive markers. We put ten QTLs along the genome controlling the expression of two traits. The location, effect and heritability of each simulated QTL are listed in Table 2. The total proportions of phenotypic variance explained by all QTLs for the two traits were 67 and 63%, respectively. The true values of the intercepts and the residual variance–covariance matrix were
We first simulated the liabilities of two traits and then artificially converted both liabilities into binary phenotypes using a threshold of zero. Only the binary responses were analysed in the present study. In this experiment, we have a total of 602 regression coefficients (one QTL per marker interval) plus a residual covariance matrix included in the model. The prior distributions given in the first experiment were also used here for the second experiment.
Table 2. Locations and effects of simulated QTL in the second simulation experiment

Each data sample was analysed using the multivariate Bayesian method developed in the present study. For all analyses, the proposed MCMC sampler was run for 52 000 sweeps and the first 2000 sweeps were discarded for the burn-in period (convergence was confirmed). The chain was trimmed by saving one observation in every 50 sweeps to reduce serial correlation. The total number of samples collected for the post-MCMC analysis was therefore 1000. The stored samples were used to infer the parameters of interest, including the locations and genetic effects of QTL as well as the means and the residual variance–covariance matrix.
The QTL intensity profiles for the three data sets in the first experiment are shown in the left panels of Fig. 1. All the plots show three major peaks within the third, the sixth and the ninth marker intervals, respectively, where the three true QTLs were located. The profiles for other intervals are almost uniform around the value of 100, as 1000 posterior samples are supposed to be distributed equally into ten shorter regions. However, as we can see from the figure, the QTL intensity profiles are not the best indicators for QTL locations. Taking the third simulated QTL for example (the QTL near a marker with a small heritability), the intensity profile for this QTL does not show clear peaks. The weighted QTL intensities (in the right panels of Fig. 1), however, show three very clear peaks, indicating precisely the positions of the simulated QTL. The weighted QTL intensity profiles are flat in regions with no simulated QTL because the estimated effects are very small using the proposed shrinkage method. As expected, there is a tendency that the first and second loci can be better detected for their larger effects. Comparing the weighted QTL intensity profiles of the three data sets, we find that the resulting peaks from data set one are generally higher than the other two data sets, while those from data set three are better than data set two. This can be explained by the numbers of continuous phenotypes included. Obviously, data sets with more continuous traits in the multiple trait set contain more information than the multiple trait set containing less number of continuous traits. The posterior means and posterior standard deviations of QTL effects are summarized in Table 3. The posterior means and posterior standard deviations of the population means and residual covariance matrix are given in Table 4. Overall, the parameter estimates are fairly close to the true parametric values (Table 1) except that the dominance effects of qtl1 are underestimated. No obvious difference is found among the three data sets with respect to the estimates of QTL effects. The precisions of the estimates from the first data set are slightly higher than those of the other two data sets.

Fig. 1. The QTL intensity profiles (left) and the weighted QTL intensity profile (right) for the three data sets in the first simulation experiment. From top to bottom are the results of data sets one, two and three, respectively.
Table 3. Bayesian estimates (posterior means and posterior standard deviations) of locations and genetic effects of QTL in the first simulation experiment

Data set one: all traits are continuous; data set two: all traits are binary; data set three: the last trait is ordinal.
Table 4. Bayesian estimates (posterior means and posterior standard deviations) of model mean and residual variance–covariance matrix in the first simulation experiment

The second simulation experiment was to investigate the efficacy of the method when applied to a large genome with more QTLs. Figure 2 shows the weighted QTL intensity profile for a random sample of the experiment. Nine clear peaks have been shown and their positions are very close to those of the true positions simulated (Table 2). The QTL located at position 1340 cM failed to be detected due to its small effects. As expected, the signal of the largest QTL (at location 35) is extremely clear, while those of QTLs at locations 140 and 650 cM are relatively weak. We can see that the method has a high resolution to separate the two closely linked QTLs (qtl1 and qtl2). The estimated QTL locations and effects for the simulated genome data are given in Table 5. Compared with Table 2 where the true effects are listed, we see that most of the effects are estimated accurately and precisely. This experiment demonstrated that the proposed Bayesian method can detect QTLs effectively when handling a large genome.

Fig. 2. The weighted QTL intensity profile for the second simulation experiment.
Table 5. Bayesian estimates (posterior means and posterior standard deviations) of locations and genetic effects of QTLs in the second simulation experiment

(ii) Rice data analysis
Blast resistance is one of the major objectives in rice (Oryza sativa L.) breeding in both tropical and temperate countries. The causal blast fungus, Pyricularia grisea, is known for its genetic instability, allowing it to overcome the genetic resistance of host plants. A framework linkage map was developed using 284 F10 recombinant inbred lines (RILs) from a ‘Lemont’בTeqing’ rice cultivar cross. Evaluation of a subset of 260 of these RILs with five races of the fungus, IC17, IB49, IB54, IG1 and IE1, was used to map resistant QTLs. In practice, biologists are usually more interested in loci with a wide spectrum of resistance than identifying resistance loci to individual races. Details of the design and the measurements of phenotypes and genotypes can be found in the original paper by Tabien et al. (2000). The original scores of the plant response were measured from grades 0–5. The average score of three replicates for each line was recorded as the observed raw data. However, we were only provided with the binary output because the investigators were more interested in QTLs responsible for the binary phenotypes. The binary phenotype of each trait was defined as w=0 if the average score was within the range 0–3 and w=1 when the score was 4–5. Each race-specific phenotype is treated as one trait here. Therefore, we have five binary traits for the multivariate Bayesian analysis. Since the mapping population was a RIL population, we need to replace the 4×4 probability transition matrix of F2 by that of a 2×2 transition matrix applied to F10 in the calculation of conditional probability of QTL genotype (Jiang & Zeng, Reference Jiang and Zeng1997).
The setup of the MCMC sampler was exactly the same as that of the simulation study. The mapping profiles are portrayed in Fig. 3, which shows that there are a total of eight resistant QTLs on chromosomes 2, 3, 11 and 12, respectively. The Bayesian estimates of locations and genetic effects of resistant QTLs are summarized in Table 6 and the estimates of model means and residual variance–covariance matrix are shown in Table 7. It is interesting to find that the same resistant QTL may have quite different responses to different races. For example, qtl2-2 was resistant to race IB54 but susceptible to the other four races. A similar pattern can be found for qtl11-2. The biological mechanisms under these results deserve further investigation.

Fig. 3. The weighted QTL intensity profiles in the ‘Lemont’בTeqing’ RIL rice population for chromosomes 1, 2, 11 and 12. Other chromosomes show no QTL effects.
Table 6. QTL mapping result for the rice blast resistance in the ‘Lemont’בTeqing’ RIL rice population. The values given in the table are the posterior means. The posterior standard deviations are given in parentheses

Table 7. Bayesian estimates (posterior means and posterior standard deviations) of the intercepts and the residual variance–covariance matrix in the ‘Lemont’בTeqing’ RIL rice population

For each component (binary) trait, we calculated the total genetic contribution (proportion of the liability variance contributed by the detected QTL). Since the experimental material is RIL, we expected to see no heterozygote. However, a small percentage (<5%) of the markers (also the QTL) are of heterozygote. We were able to modify the program to take into account the heterozygote in the model. Assume that the proportion of heterozygote for a QTL is 5%, which leads to 47·5% for each homozygote. The variance of x (coefficient for the additive effect) and the variance for z (the coefficient for the dominance effect) are 0·95 and 0·0475, respectively. The total genetic variance for a single trait is
where αk and βk are the additive and dominance effects, respectively, for the trait in question. Since the residual error variance of the liability for each trait is set to 1, the proportion of the liability variance contributed by all the detected QTLs is
We call H 2 the heritability of the trait, which is partitioned into h α2 (the additive component) and h β2 (the dominance component). These values are listed in Table 7 (the bottom line) for all the five traits. We can see that the dominance component is negligible for all traits. For the additive component, the first trait (IC17) and the last trait (IE1) have the highest heritability, i.e. these two traits are largely contributed by the additive genetic variance.
4. Discussion
In QTL mapping experiments, quantification of phenotypes generally includes use of multiple component traits, which could be different indicator traits for the evaluation of one complex agricultural character. For example, multiple physiological traits are associated with water-logging tolerance in plants, reactions to specific pathogenic races or strains in the study of rice blast resistance as discussed in the present study. Multiple traits may also be defined as several measurements of the same character under various environments or developmental stages (Zeng, Reference Zeng2005). Facilitated with the well-developed methods and software tools, investigators have a tendency to perform mapping on each trait separately and then report the results in a summary format. A more appealing approach, however, is to jointly analyse the whole suite of traits. The advantages of using the joint mapping methods over the single-trait ones have been recognized and appreciated by many researchers (Jiang & Zeng, Reference Jiang and Zeng1995; Ronin et al., Reference Ronin, Korol and Nevo1999; Knott & Haley, Reference Knott and Haley2000; Korol et al., Reference Korol, Ronin, Itskovich, Peng and Nevo2001; Cui & Wu, 2005; Xu et al., Reference Xu, Li and Xu2005; Zeng, Reference Zeng2005). Here, we briefly review some of them. First, since most of these traits are correlated genetically or environmentally, taking into account the correlation structure into the analysis can significantly increase the detection power. Second, the augmentation of observations in joint mapping method may cause reduced effect of error variance, making the estimation more precise. Third, the joint method offers an opportunity to test a series of biologically interesting hypotheses underlying the correlations between the traits. The role of genetic correlations in driving or constraining phenotypic evolution is of major interest in evolutionary genetics. Finally, and probably more meaningfully, it provides a framework within which we can understand the genetic architecture of a trait complex. However, current methods for joint mapping have only focused on the single-QTL model or the background control model (covariate markers that are in the model to control the genetic background). It is now known that when multiple QTLs are present in the same linkage group, the single-QTL model can lead to biased estimates of QTL positions and their effects. Although the composite interval mapping method for multiple traits joint analysis developed by Jiang & Zeng (Reference Jiang and Zeng1995) can reduce the biases by using multiple regression on markers outside the tested interval to absorb effects of other QTLs, the main problem of composite interval mapping in practice is how many and which markers should be chosen as covariates in the fitted model.
Most methods described above are designed for normally distributed traits. Many important traits show a binary or ordinary phenotype such as the resistance to plant disease in our example. These traits are usually explained by the threshold model, in which a fixed threshold is used to link the discrete phenotype and the latent continuous variable or liability (Lynch & Walsh, Reference Lynch and Walsh1998; Yi & Xu, Reference Yi and Xu2000). In practice, multiple discrete traits are often collected in QTL mapping experiments. Some authors (Williams et al., Reference Williams, Van Eerdewegh, Almasy and Blangero1999; Huang & Jiang, Reference Huang and Jiang2003) incorporated this situation in the context of human genetic mapping under the Identical-By-Descent (IBD)-based random model. Xu et al. (Reference Xu, Li and Xu2005) first used this idea in experimental populations by developing a joint mapping method for multiple binary characters under the ML framework. The work of Xu et al. (Reference Xu, Li and Xu2005), however, was derived in the context of interval mapping. The results from fitting the single-QTL model may result in inconsistent results as all QTL effects outside the interval are totally ignored. The extension to multiple-QTL is difficult using the conventional method, due to the large number of unobservable parameters to be estimated. The method becomes more complicated when each trait involves more than one threshold. In the present paper, we have successfully demonstrated that the proposed Bayesian mapping method can be implemented to handle the complexity of multiple ordinal traits based on the multiple-QTL model. The posterior intensity profile provides very clear signal at the simulated position of QTL, in which even a small QTL can produce a noticeable peak and closely linked loci can be well separated. Satisfactory results have also been shown in the estimation of all other parameters including QTL effects and trait correlations. The posterior variances and credibility intervals for the estimates of QTL locations and effects can also be easily obtained upon the implementation. We have further made the method applicable to multiple trait sets that contain binary trait components.
The prototype of the Bayesian shrinkage mapping was actually developed in the marker analysis of Xu (Reference Xu2003), who used the prior knowledge that most markers have negligible effects and further provided a method of discriminating the effects across markers. Similarly, in our Bayesian framework, each QTL effect vector within marker interval was assigned a multivariate normal prior distribution with mean vector zero and a unique covariance matrix. The effect-specific prior covariance matrix was further assigned an inverse-Wishart prior so that the covariance matrix can be estimated from the data. It is worth noting that the key to our success is how to choose the real positive-definite matrix Г of the inverse-Wishart prior distribution for each QTL effect vector. We found that a diagonal matrix with an identical but large element, say 105, as the pre-specified Г, can ensure that the true QTL is picked up in either the simulated data analysis or the real data analysis.
Similar to the univariate Bayesian shrinkage analysis of Xu (Reference Xu2003) and Wang et al. (Reference Wang, Zhang, Li, Masinde, Mohan, Baylink and Xu2005), our model is based on the assumption that every marker interval contains a QTL. All potential effects are included in a single model but those negligible effects are forced to shrink towards zero. One major criticism of such an approach is that it is unnecessary and unreasonable to cover such a large number of covariates, because most intervals do not include QTLs, and genotypic indicator variables of flanking short intervals are usually highly correlated. One solution is to fix these effect intervals at certain length, regardless of the number of markers contained. We have implemented this feature into our SAS program and reanalysed the data generated in the first simulation experiment with a fixed interval of 45 cM. The results are fairly similar to what we presented above but the computing time has been greatly reduced. Wang et al. (Reference Wang, Zhang, Li, Masinde, Mohan, Baylink and Xu2005), however, warned in their study that scanning intervals with larger distance may fail to detect some QTLs that can be detected by the original method. The full inclusion of the potential effects leads to another drawback of the current method that it is hard to incorporate prior knowledge about the number and the positions of QTL. The reversible-jump MCMC-based method may serve for this purpose (Sillanpaa & Arjas, 1998). Nevertheless, the proposed method is still expected to have a wide application in multi-trait analysis as it is quite straightforward and much easier to implement.
The Bayesian shrinkage analysis has been shown to be able to handle oversaturated models where the number of the model coefficients is much greater than the sample size. The special way of updating the posterior mean and posterior variances of QTL effects allows the method to selectively shrink those negligible effects. The regularization can actually be interpreted as ridge regression (Hoerl & Kennard, Reference Hoerl and Kennard1970) where the penalty added to the diagonal of the coefficient matrix is replaced by the ratio of residual variance to the variance parameters of the QTL effects. While both the proposed Bayesian method and the ridge regression achieve better prediction by shrinking the model coefficients, they cannot produce a parsimonious model as they naturally keep all predictors. Since every potential interval along the genome must be updated in each round of the iterations, our approach is more computationally intensive than the model selection methods such as the reversible-jump MCMC. Therefore, our next step is to explore a procedure in which some putative QTLs can be excluded from the model based on certain criteria. For instance, those loci constantly drawn with small effects after some consecutive cycles of iterations can be deleted from the model. A more feasible solution is to introduce the ideas of least absolute shrinkage and selection operator (LASSO) regression, which penalizes a least squares regression by the sum of the absolute values (L1-norm) of the coefficients (Tibshirani, Reference Tibshirani1996). This technique actually does both shrinkage and variable selection due to the nature of the constraint region, which often results in many coefficients becoming exactly zero. The LASSO estimate for linear regression parameters can be interpreted as a Bayesian posterior mode estimate when the priors on the regression parameters are independent double-exponential (Laplace) distributions. This posterior can also be accessed through a Gibbs sampler using conjugate normal priors for the regression coefficients, with independent exponential hyper-priors on their variances (Park & Casella, Reference Park and Casella2005).
This research was supported by the National Basic Research Program of China (grant number 2006CB101700) to C.X. and by the National Science Foundation (grant number DBI-0345205) and the USDA National Research Initiative Competitive Grants Program (USDA CSREES 2007-35300-18285) to S.X.












